1 Introduction

The no-hair conjecture, introduced by Ruffini and Wheeler in the early 1970s [1], states that stationary black holes (BHs) are characterized by only three externally observable physical parameters: mass, charge and angular momentum [2]. According to this conjecture, it is expected that external fields which are not associated with globally conserved charges would eventually be swallowed by the BH itself or be radiated away to infinity [3,4,5]. It should be noted that, however, the no-hair conjecture does not rule out the existence of nonstatic composed BH-field configurations. Considering the well-known phenomena of superradiant scattering [6], Hod first studied the dynamics of a test massive scalar field surrounding an extremal Kerr BH analytically and found that this rotating spacetime can support linearized stationary scalar clouds, exactly at the threshold of the superradiant instabilities, in its exterior region [7,8,9,10]. Using the numerical method, Herdeiro et al. first constructed Kerr BHs with non-self-interacting [11,12,13] and self-interacting [14] scalar hair at the nonlinear level, and Delgado et al. extended these studies to Kerr BHs with synchronised scalar hair and higher azimuthal harmonic index [15]. Then, Wang et al. generated a novel family of solutions of Kerr BHs with excited state scalar hair (the node number \(n\ne 0\)) [16]. In Ref. [17], García et al. further investigated the scalar clouds around Kerr BHs and discussed the obstructions towards a generalization of the no-hair conjecture. By adding charge to both the Kerr background and test scalar field, Hod observed analytically that near-extremal Kerr–Newman BHs can support linear charged scalar fields in their exterior regions [18]. Then, Benone et al. made a thorough numerical investigation of the scalar clouds due to charged scalar fields around Kerr–Newman black holes and presented the location of the existence lines for a variety of quantum numbers [19], and Huang et al. analyzed the scalar clouds and the superradiant instability regime of Kerr–Newman BHs [20]. In recent years, analogous clouds around various BHs have attracted a lot of attention, see Refs. [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] for asymptotically flat spacetimes, and Refs. [37, 38] for asymptotically anti-de Sitter spacetimes and the references therein.

As a further step along this line, we present an analysis of stationary massive scalar clouds around a rotating BH within an interesting modified gravity (MOG) model, known as the scalar–tensor–vector gravity theory. This rotating BH is dubbed as Kerr-MOG solution, since it may describe the modification from the Kerr solution [39]. In Boyer–Lindquist coordinates \((t,r,\theta ,\phi )\), the rotating Kerr-MOG BH solution has the form

$$\begin{aligned} ds^2&=-\frac{\Delta }{\rho ^2 }(cdt-a\sin ^2\theta d\phi )^2+\frac{\rho ^2}{\Delta } dr^2+\rho ^2d\theta ^2\nonumber \\&\quad +\frac{\sin ^2\theta }{\rho ^2}\left[ (r^2+a^2)d\phi -adt \right] ^2, \end{aligned}$$
(1)

where \(\rho ^2\equiv r^2+a^2\cos ^2\theta \), \(\Delta \equiv r^2-2G_N(1+\alpha )Mr+a^2+\alpha (1+\alpha ) G_N^2M^2\) with the mass parameter M, spin parameter a and dimensionless deformation parameter \(\alpha \). The deformation parameter measures deviation of MOG from general relativity [39] through the relation \(\alpha =(G-G_{N})/G_{N}\), where G and \(G_{N}\) are additional and Newtonian gravitational constants, respectively. From the viewpoint of the MOG theory, the charge parameter is proportional to the square root of the MOG parameter, i.e., \(Q=\sqrt{\alpha G_{N}}M\) [40], so the physical bound of the parameter \(\alpha \) should be \(\alpha \ge 0\). For convenience, we set \(G_N=c=1\) in the remaining of the paper. The Arnowitt–Dese–Misner (ADM) mass and angular momentum of this Kerr-MOG BH are given by \(M_{ADM}=(1+\alpha )M\) and \(J=aM_{ADM}\) [41]. Thus, two horizons of the black hole are related to the ADM mass as \(r_{\pm }=M_{ADM}\pm \sqrt{M_{ADM}^2/(1+\alpha )-a^2}\), which reduce to those of the standard Kerr case for \(\alpha =0\). It is interesting to note that the Kerr-MOG black hole has been explored extensively on various aspects, such as the observable shadows [42, 43], the thermodynamics and cosmic censorship conjecture [44,45,46,47], the geodesics and accretion disk [48,49,50,51,52], the gravitational wave [53,54,55], the superradiance [56]. Those studies reveal that there exists a significant difference between MOG and general relativity. Thus, in order to show differences between Kerr-MOG and Kerr black holes further, we initiate a study on scalar clouds around Kerr-MOG BHs in the present paper.

The structure of this paper is organized as follows. In Sect. 2 we briefly describe equation of motion of a massive scalar field propagating in the Kerr-MOG spacetime. In Sect. 3 we numerically solve the Klein–Gordon wave equation for a stationary massive scalar field and study the structure of scalar clouds, in particular the deformation parameter effects on scalar clouds, in the Kerr-MOG BHs. In Sect. 4 an analytical investigation of the Kerr-MOG scalar clouds is performed by using the matching method, and we obtain the analytical formula for the stationary bound-state resonances. We conclude in the last section with our main results.

2 Massive scalar fields in the Kerr-MOG BH background

Here we consider a physical system that consists of a massive test scalar field minimally coupled to the Kerr-MOG BH given in Eq. (1). In this BH background geometry, a massive scalar field \(\Psi \) evolves according to the Klein–Gordon equation [57]

$$\begin{aligned} (\nabla ^\nu \nabla _{\nu }-\mu ^2)\Psi =0, \end{aligned}$$
(2)

where \(\mu \) is the mass of the scalar field. In order to solve this equation, we take the following ansatz of the scalar field as

$$\begin{aligned} \Psi (t,r,\theta ,\phi )=\sum _{l,m}{R_{lm}}(r){S_{lm}}(\theta )e^{-i(\omega t-m\phi )}, \end{aligned}$$
(3)

where \(\omega \) is the conserved frequency of the wave field, l is the spherical harmonic index which is also known as the angular quantum number, and m is the azimuthal harmonic index with \(-l\le m\le l\). Substituting the decomposition (3) into the Klein–Gordon equation (2), we can get the separated differential equation for the spheroidal harmonics \(S_{lm}(\theta )\)

$$\begin{aligned}&{1\over {\sin \theta }}{{d}\over {d\theta }}\Big (\sin \theta {{d S_{lm}}\over {d\theta }}\Big ) \nonumber \\&\quad +\Big [K_{lm}+a^2(\mu ^2-\omega ^2) -a^2(\mu ^2-\omega ^2)\cos ^2\theta -{{m^2}\over {\sin ^2\theta }}\Big ]S_{lm}=0. \end{aligned}$$
(4)

Note that \(K_{lm}\) are the separation constants which have the following expansion

$$\begin{aligned} K_{lm}+a^2(\mu ^2-\omega ^2)=l(l+1)+\sum _{j=1}^{\infty }c_{j}a^{2j}(\mu ^2-\omega ^2)^{j}, \end{aligned}$$
(5)

where the coefficients \(c_{j}\) can be found in [58]. We can also obtain the radial equation for the function \(R_{lm}(r)\)

$$\begin{aligned}&\frac{d}{dr}\left( \Delta \frac{dR_{lm}}{dr}\right) \nonumber \\&+\left[ \frac{H^2}{\Delta }+2ma\omega -K_{lm}-\mu ^2(r^2+a^2)\right] R_{lm}=0, \end{aligned}$$
(6)

where we have set \(H\equiv (r^2+a^2)\omega -am\).

In order to obtain the bound-state resonances of the scalar field in the Kerr-MOG BHs, we have to investigate the asymptotic solutions of the radial equation near the horizon and at the spatial infinity with the appropriate boundary conditions. Defining a new function \(U_{lm}(r)=\sqrt{r^2+a^2}R_{lm}(r)\) and using the tortoise coordinate \(dy/dr=(r^2+a^2)/\Delta \), we can rewrite the radial Eq. (6) in the form of a Schrödinger-like wave equation

$$\begin{aligned} \frac{d^2U_{lm}}{dy^2}+(\omega ^{2}-V_{eff})U_{lm}=0, \end{aligned}$$
(7)

with the effective potential

$$\begin{aligned} V_{eff}&=\omega ^2-\frac{\Delta }{(r^2+a^2)^2}\left\{ \frac{H^2}{\Delta }+2ma\omega -K_{lm}-\mu ^2(r^2+a^2)\right. \nonumber \\&\quad \left. -\frac{\Delta +2r[r-(1+\alpha )M]}{r^2+a^2}+\frac{3r^2\Delta }{(r^2+a^2)^2}\right\} . \end{aligned}$$
(8)

Considering the physical boundary conditions of purely ingoing waves at the horizon and a decaying (bounded) solution at the spatial infinity [7,8,9,10,11,12,13], we have the following asymptotic behavior

$$\begin{aligned} R_{lm}\sim \left\{ \begin{array}{ll} e^{-i(\omega -\omega _{c})y}\;,\;\; r\rightarrow r_+~(y\rightarrow -\infty );\\ \frac{1}{r}e^{-\sqrt{\mu ^2-\omega ^2}r}\;,\;\;\; r\rightarrow \infty ~(y\rightarrow \infty ), \end{array} \right. \end{aligned}$$
(9)

with

$$\begin{aligned} \omega _{c}\equiv m\Omega _{H}=\frac{ma}{r^2_{+}+a^2}, \end{aligned}$$
(10)

where the bound state is characterized by \(\mu ^2>\omega ^2\). It should be noted that the expression (10) is just the critical frequency \(\omega _{c}\) for superradiant scattering obtained in Ref. [56]. The boundary conditions (9) single out a discrete family of complex frequencies \(\{\omega _{n}(\mu )\}\) which correspond to the bound-state resonances of the massive scalar fields. The scalar clouds, which we are interested in this paper, are characterized by \(\mathfrak {I}\omega =0\).

3 Numerical investigation of the clouds

Following Refs. [18, 19], we henceforth concentrate on the case for which the field’s frequency equals the critical one, i.e., \(\omega =\omega _{c}\), which allows the existence of stationary scalar configurations around Kerr-MOG BHs. In this section, we numerically solve the system of the field equation and investigate the structure of scalar clouds existing in the Kerr-MOG BHs.

The radial Eq. (6) can be solved numerically by doing integration from the horizon out to the infinity. Near the event horizon \(r_+\), we can expand the radial function as [19]

$$\begin{aligned} R_{lm}=R_0\left[ 1+\sum _{j\ge 1}R_{j}(r-r_+)^{j}\right] , \end{aligned}$$
(11)

with an arbitrary nonzero constant \(R_0\). The coefficients \(R_j\) may be derived straightforwardly by substituting Eq. (11) into Eq. (6). In the numerical calculations, we set \(R_0=1\) without loss of generality, and take the field mass \(\mu \) as the normalization scale to measure all other quantities. Starting with the near horizon expansion in Eq. (11) to initialize the radial function \(R_{lm}(r)\), we look for values of the rotation parameter a, for which the radial function satisfies the boundary condition at infinity given by the second relation in Eq. (9). We scan the parameter space of the system for given values of \(r_+,~\alpha ,~l\) and m. Since we would like to understand differences of scalar clouds between Kerr-MOG and Kerr BHs, in the following we focus on the effect of the dimensionless MOG parameter \(\alpha \) on the scalar clouds.

Fig. 1
figure 1

Existence lines of nodeless clouds (\(n=0\)) with fixed angular quantum numbers \(l=m=1\) and \(l=m=2\) for the parameters \(\alpha =0.0\) (black), 0.5 (red), 1.0 (blue) and 1.5 (green) in the mass vs horizon angular velocity parameter space of Kerr-MOG BHs. The dashed lines represent the extreme case, i.e., \(a=\sqrt{1+\alpha }M\), and regular BHs exist below the extremal lines

Full size image

Similarly to the Kerr case, the scalar clouds in the Kerr-MOG BHs we have obtained shall be presented in a parameter space spanned by the mass parameter M and horizon angular velocity \(\Omega _H\), which shows the impact of the parameter \(\alpha \) on the existence lines more clearly. As a matter of fact, working with either the ADM mass \(M_{ADM}\) or the mass parameter M will not qualitatively change the split behavior of the existence lines caused by the MOG parameter. The existence lines of the ground state (\(n=0\)) stationary clouds, with different MOG parameters \(\alpha \) (\(\alpha =0,0.5,1,1.5\)) and angular momentum harmonic indices \(l=m\) (\(l=m=1,2\)), are displayed in Fig. 1. Notice that in this figure, the dashed lines stand for the extremal BHs and regular BHs only exist below the extremal lines. As one may observe from this figure, regardless of the MOG parameter \(\alpha \), the existence lines move towards smaller \(\Omega _H\) with the increase of the angular quantum numbers \(l=m\). This implies that we should increase the rotation of the cloud as the rotation of the BH decreases and vice versa [11, 19]. An interesting feature presented here is that the increase of parameter \(\alpha \) make the extremal lines lower, which means that the increase of the MOG parameter can reduce the parameter space where the stationary clouds exist. Moreover, fixing the value of \(l=m\) and increasing the parameter \(\alpha \), we find that the clouds exist for lower background angular velocity for the same background mass, which implies that the higher MOG parameter corrections make it easier for the emergence of the scalar clouds. Obviously, the effect of the MOG parameter \(\alpha \) on the scalar clouds is consistent with the behavior of the effective potential shown in Fig. 2, where we observe that the potential well becomes wider and deeper as the parameter \(\alpha \) increases.

Fig. 2
figure 2

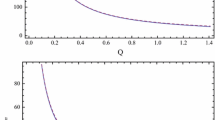
Effective potential of nodeless clouds (\(n=0\)) with the fixed angular quantum number \(l=m=1\) for the parameters \(\alpha =0.0\) (black), 0.5 (red), 1.0 (blue) and 1.5 (green) in the Kerr-MOG BH background with \(\mu r_+=0.2397\). The corresponding values of \( a\mu \) are given in the figure key

Full size image
Fig. 3
figure 3

Existence lines of nodeless clouds (\(n=0\), left) with \(m=1\), \(l=1,2,3\) and of nodeful clouds (\(n=0,1,2\), right) with \(l=m=1\) for the parameters \(\alpha =0.0\) (black) and 1.0 (red) in the mass vs horizon angular velocity parameter space of the Kerr-MOG BHs. The dashed lines represent the extreme case, i.e., \(a=\sqrt{1+\alpha }M\), and regular BHs exist below the extremal lines

Full size image

In order to further explore the impact of the MOG parameter \(\alpha \) on the scalar clouds, in Fig. 3 we exhibit the existence lines of nodeless clouds (\(n=0\)) with fixed m (\(m=1\)) but different l (\(l=1,2,3\)), and of clouds with fixed \(l=m\) (\(l=m=1\)) but different n (\(n=0,1,2\)). Interestingly enough, together with Fig. 1, we notice that the clouds with the nonzero MOG parameter move towards different values of \(\Omega _H\) as compared to the Kerr case (\(\alpha =0\)) with the same quantum numbers (l, m, n), and converge to the latter when \(M\rightarrow 0\). This indicates that the MOG parameter \(\alpha \) results in the split of the existence lines for the scalar clouds. Furthermore, fixing l or n but increasing the parameter \(\alpha \), we observe that, for the same background mass, the clouds can exist for lower background angular velocity, which supports the findings in Fig. 1 and indicates that the larger MOG parameter makes it possible for the clouds to exist in the case of the lower background angular velocity. This may be a quite general feature for the stationary scalar clouds in the Kerr-MOG BHs.

Fig. 4
figure 4

Positions of nodeless clouds (\(n=0\)) with \(l=m=1\) for the parameters \(\alpha =0.0\) (black), 0.5 (red), 1.0 (blue) and 1.5 (green) in the Kerr-MOG BH background. The dashed lines represent the extreme case, i.e., \(a=\sqrt{1+\alpha }M\)

Full size image

Finally, we analyze the “position” of the scalar clouds in order to understand how close to the horizon the clouds are concentrated. Just as in [7, 8, 19], we use \(r_{MAX}\) to denote the cloud’s position where the function \(4\pi r^2 |R_{lm}|^2\) attains its maximum value. As an example, in Fig. 4 we present the positions of nodeless clouds \(r_{MAX}/M\) as a function of a/M with \(l=m=1\) for different values of the parameter \(\alpha \) in the Kerr-MOG BH background. Obviously, decreasing a/M, the position of the clouds \(r_{MAX}/M\) increases from the minimum value in extreme case and diverges as \(a/M\rightarrow 0\), which agrees well with the fact that nonrotating MOG BHs do not support clouds. For the fixed a/M, we find that \(r_{MAX}/M\) increases as \(\alpha \) increases, which means that the clouds are concentrated at larger \(r_{MAX}\) for the Kerr-MOG BHs when compared to the Kerr BHs.

4 Analytical understanding of the clouds

In the previous section, we have studied scalar clouds in the Kerr-MOG BHs numerically. Now we proceed to study the Kerr-MOG scalar clouds analytically by using the matching method [7,8,9,10, 18, 22,23,24, 34,35,36, 59, 60]. For this purpose, we shall first divide the space outside the event horizon into two regions, namely, a far region and a near region, and then match the far-region solution and near-region solution in the overlap region to obtain the analytical formula for the stationary bound-state resonances, which describes the physical properties of these stationary scalar clouds in the Kerr-MOG BH spacetime. In order to perform analytical computation, we shall consider the eigenmode whose frequency is nearly equal to the mass of the scalar field, i.e., \(\omega \approx \mu \), which results in the relation \(|1-\omega ^{2}/\mu ^{2}|\ll 1\). Furthermore, we make an assumption [59]

$$\begin{aligned} \mathcal {O}(|\omega M|)=\mathcal {O}(|\mu M|)=\mathcal {O}(|\epsilon |), \qquad \epsilon \ll 1, \end{aligned}$$
(12)

which means that we can treat them as small parameters in the following discussions.

We first study the radial equation in the far region, i.e., \(r\gg r_{+}\), where Eq. (6) can be reduced to the form

$$\begin{aligned} \frac{d^2(rR_{lm})}{dr^2}&+ \left[ \omega ^2-\mu ^2+\frac{2(1+\alpha )(2M\omega ^2 -M\mu ^2)}{r}\right. \nonumber \\&\quad \left. -\frac{l(l+1)+\epsilon ^2}{r^2}\right] (rR_{lm})=0. \end{aligned}$$
(13)

Defining

$$\begin{aligned} x=-2ikr=-2i\sqrt{\omega ^2-\mu ^2}r, \end{aligned}$$
(14)

the above equation becomes

$$\begin{aligned} {{d^2(rR_{lm})}\over {dx^2}}+\left[ -\frac{1}{4}+\frac{\nu }{x} +\frac{1}{x^{2}}\left( \frac{1}{4}-\beta ^{2}\right) \right] (rR_{lm})=0,\nonumber \\ \end{aligned}$$
(15)

with

$$\begin{aligned} \nu =\frac{i(1+\alpha )(2M\omega ^2-M\mu ^2)}{k}, \quad \beta =l+\frac{1}{2}+\frac{\epsilon ^2}{2l+1}.\nonumber \\ \end{aligned}$$
(16)

It is obvious that Eq. (15) is the standard Whittaker equation, so that the solution \(R_{lm}(r)\) may be written in terms of a confluent hypergeometric function [58]

$$\begin{aligned} rR_{lm}\sim (-2ikr)^{l+1}e^{ikr}U(l+1+\epsilon ^2-\nu ,2l+2+2\epsilon ^2;-2ikr),\nonumber \\ \end{aligned}$$
(17)
Fig. 5
figure 5

Comparison between the numerical result (red) and the analytical formula by the matching method (green) for nodeless clouds (\(n=0\)) with fixed angular quantum numbers \(l=m=1\) and \(l=m=2\) for the parameters \(\alpha =0\) (left) and 1.0 (right) in the Kerr-MOG BH background

Full size image
Fig. 6
figure 6

Comparison between the numerical result (red) and the analytical formula by the matching method (green) for nodeless clouds (\(n=0\)) with \(m=1\) and \(\alpha =1.0\) for different angular quantum numbers \(l=1\), 2, 3 and 4 in the Kerr-MOG BH background

Full size image
Fig. 7
figure 7

Comparison between the numerical result (red) and the analytical formula by the matching method (green) for the clouds (\(n=0,1,2\) and 3) with \(l=m=1\) for the parameter \(\alpha =1.0\) in the Kerr-MOG BH background

Full size image

where a decaying boundary condition, given in Eq. (9), has been imposed. In order to match with the near region solution, we expand the solution (17) for \(|kr|\ll 1\) as

$$\begin{aligned} \begin{aligned}&rR_{lm}\sim \frac{(-2ikr)^{l+1}\pi }{\sin \left[ \pi (2l+2+2\epsilon ^2)\right] }\left[ \frac{1}{\Gamma (-l-\nu -\epsilon ^2)\Gamma (2l+2+2\epsilon ^2)}+\cdots \right. \\&\quad \left. -\frac{(-2ikr)^{-2l-1}}{\Gamma (-2l-2\epsilon ^2)\Gamma (1+l-\nu +\epsilon ^2)}+\cdots \right] . \end{aligned} \end{aligned}$$
(18)

We next discuss the radial equation in the near region, i.e., \(r\ll l/\mu \), where Eq. (6) can be expressed as

$$\begin{aligned} z(1-z)\frac{d^2R_{lm}}{dz^2}+(1-z)\frac{dR_{lm}}{dz}+\left[ p^2\frac{1-z}{z}-\frac{l(l+1)}{1-z}\right] R_{lm}=0, \end{aligned}$$
(19)

with

$$\begin{aligned} z\equiv \frac{r-r_+}{r-r_-},\qquad p\equiv -\frac{(r_+^2+a^2)\omega -ma}{r_+-r_-}. \end{aligned}$$
(20)

We assume that the radial function \(R_{lm}(z)\) takes the form

$$\begin{aligned} R_{lm}=z^{ip}(1-z)^{l+1}F(z), \end{aligned}$$
(21)

so the resulting equation of motion for F(z) is found to be

$$\begin{aligned} z(1-z)\frac{d^2F}{dz^2}+\left[ c-(a+b+1)z\right] \frac{dF}{dz}+abF=0, \end{aligned}$$
(22)

with

$$\begin{aligned} a=l+1,\qquad b=l+1+2ip,\qquad c=1+2ip. \end{aligned}$$
(23)

It is interesting to note that Eq. (22) is the standard hypergeometric equation [58]. Therefore, we obtain the radial solution

$$\begin{aligned} R_{lm}\sim z^{ip}(1-z)^{l+1}F(a,b,c;z), \end{aligned}$$
(24)

where F(a, b, c; z) is the hypergeometric function [58], and the ingoing wave boundary condition, given in Eq. (9), has been imposed. To achieve large r behavior, we use the \(z\rightarrow 1-z\) transformation for the hypergeometric function

$$\begin{aligned} F(a,b,c;z)= & {} \frac{\Gamma (c)\Gamma (c-a-b)}{\Gamma (c-a)\Gamma (c-b)}\nonumber \\&F(a,b,a+b-c+1;1-z)\nonumber \\&+(1-z)^{c-a-b}\frac{\Gamma (c)\Gamma (a+b-c)}{\Gamma (a)\Gamma (b)}\nonumber \\&F(c-a,c-b,c-a-b+1;1-z),\nonumber \\ \end{aligned}$$
(25)

and the property \(F(a,b,c;0)=1\). Accordingly, the large r behavior of the solution (24) is given by

$$\begin{aligned}&R_{lm}\sim \frac{\Gamma (1+2ip)\Gamma (2l+1)}{\Gamma (l+1)\Gamma (l+1+2ip)} \left( \frac{r}{r_+-r_-}\right) ^l\nonumber \\&\quad +\frac{\Gamma (1+2ip)\Gamma (-2l-1)}{\Gamma (-l)\Gamma (-l+2ip)}\left( \frac{r}{r_+-r_-}\right) ^{-l-1}, \end{aligned}$$
(26)

where we have noted that \(1-z\rightarrow (r_+-r_-)/r\) in the limit of large r.

Now we are in a position to match the far-region solution and near-region solution in the overlap region \(r_+\ll r\ll 1/(2\sqrt{\mu ^{2}-\omega ^{2}})\) [59]. From the expressions (18) and (26), we arrive at

$$\begin{aligned}&\frac{\Gamma (l+1)\Gamma (-2l-1)}{\Gamma (-l)\Gamma (2l+1)}\frac{\Gamma (l+1+2ip)}{\Gamma (-l+2ip)}\left[ -2ik(r_+-r_-)\right] ^{2l+1}\nonumber \\&\quad =\frac{\Gamma (-l-\nu -\epsilon ^2)\Gamma (2l+2+2\epsilon ^2)}{\Gamma (l- \nu +1+\epsilon ^2)\Gamma (-2l-2\epsilon ^2)}. \end{aligned}$$
(27)

It is clear that the left hand side of Eq. (27) is \(\mathcal {O}((k(r_+-r_-))^{2l+1})\) for \(\omega \approx \mu \) and \(k(r_+-r_-)\ll 1\), which tells us that at the leading order of \(\nu \) the right hand side of this equation equals zero. Assuming \(\nu \equiv \nu _{0}+\delta \nu \), we then obtain

$$\begin{aligned} \frac{\Gamma (-l-\nu _{0}-\epsilon ^2)\Gamma (2l+2+2\epsilon ^2)}{\Gamma (l- \nu _{0}+1+\epsilon ^2)\Gamma (-2l-2\epsilon ^2)}=0. \end{aligned}$$
(28)

Considering the property of the gamma function \(1/\Gamma (-n)=0\), we get

$$\begin{aligned} l-\nu _{0}+1+\epsilon ^2=-n, \end{aligned}$$
(29)

where \(n\ge 0\) is a non-negative integer. Expressing \(\omega \) as \(\omega \equiv \omega _{0}+\delta \omega \), from Eq. (16) we observe that

$$\begin{aligned} \nu _{0}=\frac{i(1+\alpha )(2M\omega _{0}^2-M\mu ^2)}{\sqrt{\omega _{0}^2-\mu ^2}}\approx l+n+1, \end{aligned}$$
(30)

which leads to the analytical formula

$$\begin{aligned} \omega _{0}\approx & {} \mu \left\{ 1-\left[ \frac{(1+\alpha )M\mu }{l+n+1}\right] ^2\right\} ^{1/2}\nonumber \\\approx & {} \mu \left\{ 1-\frac{1}{2}\left[ \frac{(1+\alpha )M\mu }{l+n+1}\right] ^2\right\} . \end{aligned}$$
(31)

From both the superradiance condition, given in Eq. (10), and the above formula, one may easily deduce that scalar clouds satisfy

$$\begin{aligned} \dfrac{\Omega _H}{\mu }\approx & {} \dfrac{1}{m}\left\{ 1-\left[ \frac{(1+\alpha )M\mu }{l+n+1}\right] ^2\right\} ^{1/2}\nonumber \\\approx & {} \dfrac{1}{m}\left\{ 1-\frac{1}{2}\left[ \frac{(1+\alpha )M\mu }{l+n+1}\right] ^2\right\} . \end{aligned}$$
(32)

Obviously, in the regime \(M\mu \ll 1\), the dependence of scalar clouds on various parameters \(\alpha \), \(M\mu \), l and n is clearly given by the above expression.

In order to verify the validity of the matching method, we compare the numerical results against the analytical ones. In Fig. 5, we present the analytical results obtained by using the matching method and the numerical data for the ground state \(n=0\) with different angular quantum numbers \(l=m\) and MOG parameters \(\alpha \). It is shown that the analytical formula, derived in Eq. (32), is in very good agreement with the numerical calculation, even for the large mass coupling \(M\mu \). From Fig. 5, we also observe that the consistence between analytical results and numerical data may be improved by increasing the MOG parameter \(\alpha \) or decreasing the angular quantum number \(l=m\).

Similarly, we further compare the analytical formula (32) with the numerical results for the ground state clouds \(n=0\) with \(m=1\), \(\alpha =1.0\) and \(l=1\), 2, 3, 4 in Fig. 6, and for the clouds \(n=0,1,2,3\) with \(l=m=1\), \(\alpha =1.0\) in Fig. 7. Again, the agreement between the analytical and numerical results shown in these two figures is impressive. Moreover, from Figs. 6 and 7, if the angular quantum number l (fixing m) or the node number n increases, we can further improve our analytical results and improve the consistency with the numerical findings.

The comparison between the analytical and numerical results indicates that the matching method is a powerful tool to investigate the scalar clouds in the Kerr-MOG BHs. From the expression (32), we can obtain the dependence of the results on the MOG parameter \(\alpha \) directly, i.e., \(\Omega _H/\mu \) will decrease as the parameter \(\alpha \) increases for the fixed \(M\mu \), l and n, which can be used to back up the numerical finding as shown in the previous section that the larger MOG parameter makes it possible for the clouds to exist in the case of the lower background angular velocity.

5 Conclusions

We have investigated the scalar clouds around a rotating BH in modified gravity theory, called the Kerr-MOG BH, by using both the numerical and analytical methods. Solving the Klein–Gordon wave equation for a scalar field with the mass \(\mu \) in the BH background, the stationary bound-state solutions may be characterized by the existence lines in the parameter space of the Kerr-MOG BH. We found that the larger of the MOG parameter, the smaller of parameter space where the stationary clouds exist. We further observed that, with the fixed quantum numbers (l, m, n), the solutions with the nonzero MOG parameter move towards different values of the angular velocity \(\Omega _H\) as compared to the Kerr case, and converge to the latter when the mass \(M\rightarrow 0\), which means that the MOG parameter results in the split of the existence lines for the scalar clouds. Interestingly, fixing the values of (l, m, n) but increasing \(\alpha \), we noticed that the clouds, for the same background mass, exist for lower background angular velocity. This fact agrees well with the behavior of the effective potential and indicates that the larger MOG parameter makes it possible for the clouds to exist in the case of the lower background angular velocity. In order to understand the numerical results, we also employed an analytical matching method to study the Kerr-MOG scalar clouds and found that the analytical formula obtained by this method is in very good agreement with the numerical data, even for the large \(M\mu \). This implies that the matching method is a powerful analytical way to investigate the scalar clouds existing in the Kerr-MOG BHs. Moreover, we presented the location of the existence lines and showed that the clouds are concentrated at the larger radial position for the Kerr-MOG BHs when compared to the Kerr BHs. The present work is carried out at the linear level, and the existence of scalar clouds indicates nonlinear hairy BH solutions [11,12,13]. It will then be interesting to construct the nonlinear realization of scalar clouds in Kerr-MOG BHs, and we will leave it for further study in the near future.