Evasion of HSR in the charmless decays of excited P-wave charmonia

Abstract

We investigate the charmless decays of excited P-wave charmonia $\chi _{c1}^\prime \rightarrow VV$ and $\chi _{c2}^\prime \rightarrow VP$ via intermediate charmed meson loops, where V and P denote the light vector and pseudoscalar mesons, respectively. Within the model parameters, the charmed meson loop contributions are evaluated by using the effective Lagrangian approach. For $\chi _{c1}^\prime \rightarrow VV$, the partial widths of the $\rho \rho$, $\omega \omega$, and $K^*{\bar{K}}^*$ channels can reach to the order of MeV, while the partial width of the $\phi \phi$ channel is very small and in the order of keV. For $\chi _{c2}^\prime \rightarrow V P$, the partial widths of $\chi _{c2}^{\prime } \rightarrow K^*\bar{K}+c.c$ turns out to be sizeable, while the partial widths of $\chi _{c2}^{\prime } \rightarrow \rho ^+\pi ^- +c.c$ is found to be much smaller than the $K^*\bar{K}+c.c$ channel. Our calculations may be examined by the future BESIII experiments.

1 Introduction

The energy region of charmonium contains rich information about both perturbative and nonperturbative QCD dynamics. By studying the exclusive decays of charmonium, we expect to obtain some insights into the QCD properties in this regime. The charmless decay modes of charmonium states are suppressed according to the Okubo–Zweig–Iizuka (OZI) rule. But, these charmless decays are crucial to understand the dynamical properties of QCD. For example, in the perturbative QCD (pQCD) approach, if one considers only the valence Fock state $c\bar{c}$, the branching ratios of the charmless decay $J_{c\bar{c}}(\lambda ) \rightarrow h_1(\lambda _1) h_2(\lambda _2)$ can be written as [1],

$$\begin{aligned} {\text{ BR }}[{J_{c\bar{c}}(\lambda )} \rightarrow h_1(\lambda _1) h_2(\lambda _2)] \sim \left( \frac{\Lambda _{QCD}^2}{m_c^2}\right) ^{|\lambda _1 + \lambda _2| +2} \, , \end{aligned}$$

(1)

where $J_{c \bar{c}}$, $h_1$ and $h_2$ are the initial charmonium meson and final two light mesons, respectively. $\lambda$, $\lambda _1$, and $\lambda _2$ are the helicities of the corresponding mesons. From Eq. (1), one can see that the leading contribution corresponds to the $\lambda _1+\lambda _2 = 0$ condition, while the helicity configurations that do not satisfy this relation will be suppressed. This is the so-called helicity selection rule (HSR).

This HSR can alternatively be described with the “naturalness” quantum number of relevant particle $\sigma \equiv P(-1)^J$, where P and J are the parity and spin of the particle, respectively. The HSR then requires that $\sigma ^\mathrm{{initial}} = \sigma _1\sigma _2$, which means that the naturalness of initial state equals to the product of the final states [1,2,3]. If $\sigma ^\mathrm{{initial}}\ne \sigma _1\sigma _2$, one have to add a Levi–Civita (LC) tensor $\varepsilon _{\alpha \beta \mu \nu }$ in the amplitude to keep the parity conservation and Lorentz invariance. The LC tensor are contracted with the polarization vectors and momenta of the involved mesons, hence there are some terms vanished in the helicity amplitudes, and these contributions are supposed to be suppressed by pQCD.

On the other hand, intermediate meson loop (IML) is regarded as an important nonperturbative transition mechanism in the charmonium energy region [4,5,6,7]. Recently, this mechanism has been successfully applied to study the production and decays of charmonium and exotic states [8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38]. Some exclusive decay modes of charmonia below the open $D\bar{D}$ threshold will be suppressed by both OZI rule and HSR and there shows significant discrepancies between the experimental measurements and the theoretical expectations [39]. In the previous works [40,41,42,43,44], the HSR violating processes of the charmonium states decaying into the light vector mesons, pseudoscalar mesons, or baryon-anti-baryon pairs were studied. The results indicate that the IML transitions are important to reproduce the experimental data on these decays, although there are still some model-dependent parameters needed to be determined with more accurate data. To give a consistent theoretical description and search for the underlying dynamic mechanism, investigating many other pertinent HSR violating decay modes turns to be necessary.

In Ref. [42], the P-wave ground states HSR suppressed decays $\chi _{c1} \rightarrow VV$ and $\chi _{c2}\rightarrow VP$ were studied via intermediate charmed meson loops. In this paper, we will further investigate the excited P-wave states HSR suppressed decays $\chi _{c1}^\prime \rightarrow VV$ and $\chi _{c2}^\prime \rightarrow VP.$¹ Since the $\chi _{c1}^\prime$ and $\chi _{c2}^\prime$ are above the open charmed meson pairs, it is expected that the IML mechanims should be more important in the above HSR violating processes.

The paper is organized as follows. We present our model and ingredients of the effective Lagrangians and decay amplitudes in Sect. 2. The numerical results are shown in Sect. 3 and the summary is presented in Sect. 4.

2 The model

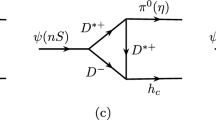
Following Ref. [42], we consider the contributions of intermediate meson loops as illustrated in Figs. 1 and 2 for the decays of $\chi _{c1}^{\prime } \rightarrow VV$ and $\chi _{c2}^{\prime } \rightarrow VP$, respectively. In fact, we should also take other possible intermediate meson loops into account. Since $\chi _{cJ}^{\prime }$ couple to two charmed mesons in S-wave and the masses of $\chi _{cJ}^{\prime }$ are near the mass threshold of the charmed mesons pairs, we consider the IML illustrated in Figs. 1 and  2 as the leading order contributions for the $\chi _{c1}^{\prime } \rightarrow VV$ and $\chi _{c2}^{\prime } \rightarrow VP$ decays. Note that $\chi '_{c2}$ couples to $D\bar{D}$ in D-wave, however, this contribution is much smaller compared with the contributions shown in Fig. 2, and they are safely neglected.

Fig. 1

The hadron-level diagrams for charmless decay modes $\chi _{c1}^{\prime } \rightarrow VV$ via intermediate charmed meson loops

Fig. 2

The hadron-level diagrams for charmless decay modes $\chi _{c2}^{\prime } \rightarrow VP$ via intermediate charmed meson loops

To calculate the decay amplitudes of these diagrams, we need the effective interaction Lagrangians for each vertex of Figs. 1 and 2. Based on the heavy quark limit and chiral symmetry [45,46,47], the Lagrangian for the P-wave charmonia at leading order is given by

$$\begin{aligned} \mathcal L_1= & {} i{g_1}Tr\left[ {P^\mu _{c \bar{c}}}{\bar{H}_{2i}}\gamma ^\mu {\bar{H}_{1i}} \right] +h.c., \end{aligned}$$

(2)

where the spin multiplets for these P-wave charmonium states are expressed as:

$$\begin{aligned} P^\mu _{c \bar{c}}= & {} \frac{1 + \not v}{2}\left( \chi ^{\mu \alpha }_{c2}\gamma _{\alpha }+\frac{1}{\sqrt{2}}\epsilon _{\mu \nu \alpha \beta }v^{\alpha }\gamma ^{\beta }\chi ^{\nu }_{c1} \right. \nonumber \\&\left. +\frac{1}{\sqrt{3}}(\gamma ^{\mu }-v^{\mu })\chi _{c0} +h^\mu _c\gamma _5 \right) \frac{1 - \not v}{2} \, , \end{aligned}$$

(3)

with $v^\mu$ being the four-velocity of the multiplets. Besides, the charmed and anti-charmed mesons triplets read as:

$$\begin{aligned} H_{1i}= & {} \frac{1 + \not v}{2}\left[ \mathcal{D}_{i\mu }^* \gamma _\mu - \mathcal{D}_i \gamma _5 \right] ,\nonumber \\ H_{2i}= & {} \left[ {\bar{\mathcal{D}}}_{i\mu }^*\gamma _\mu + {\bar{\mathcal{D}}}_i\gamma _5 \right] \frac{1 - \not v}{2}, \end{aligned}$$

(4)

where $\mathcal{D}$ and $\mathcal{D}^*$ denote the pseudoscalar and vector charmed meson fields, respectively, i.e. $\mathcal{D}^{(*)} = (D^{(*)+}, D^{(*)0}, D^{(*)+}_{s})$. $v^\mu$ is the four-velocity of the intermediate charmed mesons. $\varepsilon _{\mu \nu \alpha \beta }$ is the antisymmetric LC tensor and $\varepsilon _{0123}=+1$.

Consequently, the explicit Lagrangian of P-wave charmonium $\chi _{cJ}$ is expressed as,

$$\begin{aligned} \mathcal {L}_{P}= & {} i g_{\chi _{c0} \mathcal{D} \mathcal{D}} \mathcal{D}^i \mathcal{D}_i^\dag + i g_{\chi _{c0} \mathcal{D}^* \mathcal{D}^*} \mathcal{D}^{*i}_\mu \mathcal{D}_i^{*\mu \dag } \nonumber \\&+g_{\chi _{c1} \mathcal{D}^{*} \mathcal{D}} \chi _{c1}^\mu (\mathcal{D}^*_{i\mu } \mathcal{D}^{i\dag }+\mathcal{D}_i \mathcal{D}^{i\mu \dag } ) \nonumber \\&+i g_{\chi _{c2} \mathcal{D}^{*} \mathcal{D}^{*}} \chi _{c2}^{\alpha \beta } (\mathcal{D}_{\alpha }^{i*} \mathcal{D}_{i\beta }^{* \dagger }+ \mathcal{D}_{\beta }^{i*} \mathcal{D}_{i\alpha }^{* \dagger }) \, , \end{aligned}$$

(5)

where the coupling constants will be discussed in the following.

In addition, the Lagrangians relevant to the light vector and pseudoscalar mesons can be constructed based on the heavy quark limit and chiral symmetry,

$$\begin{aligned} \mathcal{L}= & {} -ig_{\mathcal{D}^{*}\mathcal{D} {\mathcal P}}\left( \mathcal{D}^i \partial ^\mu {\mathcal P}_{ij} \mathcal{D}_\mu ^{*j\dagger }-\mathcal{D}_\mu ^{*i}\partial ^\mu {\mathcal P}_{ij} \mathcal{D}^{j \dag }\right) \nonumber \\&+\frac{1}{2}g_{\mathcal{D}^*D^*{\mathcal P}}\varepsilon _{\mu \nu \alpha \beta }\mathcal{D}_i^{*\mu }\partial ^\nu {\mathcal P}^{ij} {\overset{ \leftrightarrow }{\partial }}{\!^{\alpha }} \mathcal{D}_j^{*\beta \dag } \nonumber \\&-2f_{\mathcal {D}^*\mathcal {D}\mathcal {V}} \epsilon _{\mu \nu \alpha \beta } (\partial ^\mu \mathcal {V}^\nu )^i_j (\mathcal {D}_i^\dagger {{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!^\alpha } \mathcal {D}^{*\beta j}-\mathcal {D}_i^{*\beta \dagger }{{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!^\alpha } \mathcal{D}^j) \nonumber \\&- ig_{\mathcal {D}\mathcal {D}\mathcal {V}} \mathcal {D}_i^\dagger {{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!_\mu } \mathcal {D}^j(\mathcal {V}^\mu )^i_j + ig_{\mathcal {D}^*\mathcal {D}^*\mathcal {V}} \mathcal {D}^{*\nu \dagger }_i {{\mathop {\partial }\limits ^{\leftrightarrow }}}{\!_\mu } \mathcal {D}^{*j}_\nu (\mathcal {V}^\mu )^i_j \nonumber \\&+4if_{\mathcal {D}^*\mathcal {D}^*\mathcal {V}} \mathcal {D}^{*\dagger }_{i\mu }(\partial ^\mu \mathcal {V}^\nu -\partial ^\nu \mathcal {V}^\mu )^i_j \mathcal {D}^{*j}_\nu +\mathrm{H.c.} , \end{aligned}$$

(6)

where $\mathcal P$ and ${\mathcal V}_\mu$ are $3\times 3$ matrices for the octet pseudoscalar and nonet vector mesons, respectively,

$$\begin{aligned} \mathcal {P}= & {} \left( \begin{array} {ccc} \frac{\pi ^0}{\sqrt{2}} +\frac{\eta }{\sqrt{6}} &{} \pi ^+ &{} K^+ \\ \pi ^- &{} -\frac{\pi ^0}{\sqrt{2}} +\frac{ \eta }{\sqrt{6}} &{} K^0 \\ K^-&{} {\bar{K}}^0 &{} -\sqrt{\frac{2}{3}}\eta \\ \end{array}\right) , \end{aligned}$$

(7)

$$\begin{aligned} \mathcal {V}_\mu= & {} \left( \begin{array}{ccc}\frac{\rho ^0}{\sqrt{2}}+\frac{\omega }{\sqrt{2}}&{}\rho ^+ &{} K^{*+} \\ \rho ^- &{} -\frac{\rho ^0}{\sqrt{2}} + \frac{\omega }{\sqrt{2}} &{} K^{*0} \\ K^{*-}&{} {\bar{K}}^{*0} &{} \phi \\ \end{array}\right) _\mu \, . \end{aligned}$$

(8)

Then we can write the explicit transition amplitudes for $\chi _{c1}^{\prime }(p_1)\rightarrow [D^{(*)}(q_1) {\bar{D}}^{(*)}(q_3)] D^{(*)}(q_2) \rightarrow V_1(p_2)V_2(p_3)$ as follows:

$$\begin{aligned} \mathcal {M}_a= & {} \int \frac{d^4q_2}{(2\pi )^4} [g_{\chi _{c1}^{\prime }D^*D}\epsilon _{1\alpha }][-g_{DDV} (q_1+q_2)_\mu \epsilon _2^{*\mu }] \nonumber \\&\times [2f_{D^*DV} \varepsilon _{\kappa \lambda \rho \sigma } p_3^\kappa \epsilon _3^{*\lambda } (q_2-q_3)^\rho ] \frac{i}{q_1^2-m_1^2}\nonumber \\&\times \frac{i}{q_2^2-m_2^2} \frac{i(-g^{\alpha \sigma }+{q^\alpha _3q^\sigma _3}/{m_3^2})}{q_3^2-m_3^2} \mathcal{F}(q^2), \nonumber \\ \mathcal {M}_b= & {} \int \frac{d^4q_2}{(2\pi )^4} [g_{\chi _{c1}^{\prime }D^*D}\epsilon _{1\alpha }][2f_{D^*DV} \varepsilon _{\mu \nu \theta \phi } (q_1+q_2)^\theta \nonumber \\&\times p_2^\mu \epsilon _2^{*\phi } ] [g_{D^*D^*V} (q_2-q_3)_\rho g_{\lambda \sigma }\epsilon _3^{*\rho } -4f_{D^*D^*V} \nonumber \\&\times (p_{3\sigma }g_{\lambda \rho }-p_{3\lambda }g_{\sigma \rho })\epsilon _3^{*\rho }]\frac{i}{q_1^2-m_1^2} \nonumber \\&\times \frac{i(-g^{\nu \lambda }+{q^\nu _2q^\lambda _2}/{m_2^2})}{q_2^2-m_2^2}\frac{i(-g^{\alpha \sigma }+{q^\alpha _3q^\sigma _3}/{m_3^2})}{q_3^2-m_3^2} \mathcal{F}(q^2), \nonumber \\ \mathcal {M}_c= & {} \int \frac{d^4q_2}{(2\pi )^4} [g_{\chi _{c1}^{\prime }D^*D}\epsilon _{1\alpha }][-2f_{D^*DV} \varepsilon _{\mu \nu \theta \phi } (q_1+q_2)^\theta ]\nonumber \\&\times p_2^\mu \epsilon _2^{*\nu } [-g_{DDV}(q_2-q_3)_\kappa \epsilon _3^{*\kappa }] \frac{i(-g^{\alpha \phi }+{q^\alpha _1q^\phi _1}/{m_1^2})}{q_1^2-m_1^2} \nonumber \\&\times \frac{i}{q_2^2-m_2^2} \frac{i}{q_3^2-m_3^2} \mathcal{F}(q^2), \nonumber \\ \mathcal {M}_d= & {} \int \frac{d^4q_2}{(2\pi )^4} [g_{\chi _{c1}^{\prime }D^*D}\epsilon _{1\alpha }] [g_{D^*D^*V} (q_1+q_2)_\phi g_{\mu \theta }\epsilon _2^{*\phi } \nonumber \\&-4f_{D^*D^*V}(p_{2\theta }g_{\mu \phi }-p_{2\mu }g_{\theta \phi })\epsilon _2^{*\phi }][2f_{D^*DV} \varepsilon _{\kappa \lambda \rho \sigma } \nonumber \\&\times p_3^\kappa \epsilon _3^{*\lambda } (q_2-q_3)^\rho ] \frac{i(-g^{\alpha \mu }+{q^\alpha _1q^\mu _1}/{m_1^2})}{q_1^2-m_1^2}\nonumber \\&\times \frac{i(-g^{\theta \sigma }+{q^\theta _2q^\sigma _2}/{m_2^2})}{q_2^2-m_2^2} \frac{i}{q_3^2-m_3^2} \mathcal{F}(q^2) \, , \end{aligned}$$

(9)

where $p_1$ ($\varepsilon _1$), $p_2$ ($\varepsilon _2$) and $p_3$ ($\varepsilon _3$) are the four-momenta (polarization vector) of the initial state $\chi _{c1}^{\prime }$, final state $V_1$ and $V_2$, respectively. $q_1$, $q_2$ and $q_3$ are the four-momenta of the up, right and down charmed mesons in the triangle loop, respectively.

Similarly, the explicit transition amplitudes for $\chi _{c2}^{\prime }(p_1)\rightarrow [D^{(*)}(q_1) {\bar{D}}^{(*)}(q_3)] D^{(*)}(q_2) \rightarrow V(p_2)P(p_3)$ are given by

$$\begin{aligned} \mathcal {M}_a= & {} \int \frac{d^4q_2}{(2\pi )^4} [ig_{\chi _{c2}^{\prime }D^*D^*}\epsilon _{1\alpha \beta }] [2f_{D^*DV} \varepsilon _{\mu \nu \theta \phi } (q_1+q_2)^\theta ] \nonumber \\&\times p_2^\mu \epsilon _2^{*\nu } [g_{D^*DP}p_3^\kappa ]\frac{i(-g^{\alpha \phi }+{q^\alpha _1 q^\phi _1}/{m_1^2})}{q_1^2-m_1^2} \nonumber \\&\times \frac{i}{q_2^2-m_2^2} \frac{i(-g^{\beta \kappa }+{q^\beta _3q^\kappa _3}/{m_3^2})}{q_3^2-m_3^2} \mathcal{F}(q^2), \end{aligned}$$

(10)

$$\begin{aligned} \mathcal {M}_b= & {} \int \frac{d^4q_2}{(2\pi )^4} [ig_{\chi _{c2}^{\prime }D^*D^*}\epsilon _{1\alpha \beta }] [g_{D^*D^*V} (q_1+q_2)_\phi g_{\mu \theta }\epsilon _2^{*\phi } \nonumber \\&-4f_{D^*D^*V}(p_{2\theta }g_{\mu \phi }-p_{2\mu }g_{\theta \phi })\epsilon _2^{*\phi }]\nonumber \\&\times [-\frac{1}{2}g_{D^*D^*P}\varepsilon _{\kappa \lambda \rho \sigma }p_3^\lambda q_2^\rho ]\frac{i(-g^{\alpha \mu }+{q^\alpha _1q^\mu _1}/{m_1^2})}{q_1^2-m_1^2} \nonumber \\&\times \frac{i(-g^{\theta \kappa }+{q^\theta _2q^\kappa _2}/{m_2^2})}{q_2^2-m_2^2} \frac{i(-g^{\beta \sigma }+{q^\beta _3q^\sigma _3}/{m_3^2})}{q_3^2-m_3^2} \mathcal{F}(q^2) \, , \nonumber \\ \end{aligned}$$

(11)

with $\varepsilon _1$ the polarization tensor of initial state $\chi _{c2}^{\prime }$.

In the triangle diagrams of Figs. 1 and 2, the intermediate charmed mesons are usually off-shell. To compensate the off shell effects and regularize the ultraviolet divergence [48,49,50], we adopt the following form factors,

$$\begin{aligned} \mathcal{F}(q^2) \equiv \prod _i \left( \frac{\Lambda _i^2-m_{i}^2}{\Lambda _i^2-q_i^2}\right) , \end{aligned}$$

(12)

where $i=1,2,3$ corresponds three intermediate mesons, respectively. $\Lambda _i \equiv m_i+\alpha \Lambda _\mathrm{QCD}$ and the QCD energy scale $\Lambda _\mathrm{QCD} = 220$ MeV. In the present work, the model parameter $\alpha$ is constrained between 0.2 and 0.4 for $\chi '_{c1} \rightarrow VV$ decays, and 0.4 and 0.8 for $\chi '_{c2} \rightarrow VP$ decays. It is worth to mention that, with the values of $\alpha$ in the above range, the experimental data on the decays of $\chi _{c1} \rightarrow VV$ and $\chi _{c2} \rightarrow VP$ can be well reproduced [42].

3 Numerical results

In this section, we first determine the coupling constants in the above section and then present our numerical results. Under the heavy quark limit, the coupling constants of P-wave charmonium coupled to the charmed mesons are as follows [32, 45]:

$$\begin{aligned} g_{\chi _{c1}^{\prime }\mathcal{D}^*\mathcal{D}}= & {} 2\sqrt{2}g_1 \sqrt{m_{\chi _{c1}^{\prime }} m_\mathcal{D} m_{\mathcal{D}^*}} \, , \end{aligned}$$

(13)

$$\begin{aligned} g_{\chi _{c2}^{\prime }\mathcal{D}^*\mathcal{D}^*}= & {} 4g_1 m_{\mathcal{D}^*}\sqrt{m_{\chi _{c2}^{\prime }}} \, , \end{aligned}$$

(14)

with $g_1 =1.28$ GeV$^{-1/2}$, which is obtained in the linear potential model [51, 52]. Besides, the charmed meson couplings to the light vector mesons are obtained with [45, 47],

$$\begin{aligned} g_{\mathcal{D}\mathcal{D}V}= & {} g_{\mathcal{D}^*\mathcal{D}^*V} = \frac{\beta g_V}{\sqrt{2}} , \end{aligned}$$

(15)

$$\begin{aligned} f_{\mathcal{D}^*\mathcal{D}V}= & {} \frac{ f_{\mathcal{D}^*\mathcal{D}^*V}}{m_{\mathcal{D}^*}}=\frac{\lambda g_V}{\sqrt{2}} \, , \end{aligned}$$

(16)

$$\begin{aligned} g_{\mathcal {D}^{*} \mathcal {D} \mathcal {P}}= & {} \frac{2 g}{f_{\pi }} \sqrt{m_{\mathcal {D}} m_{\mathcal {D}^{*}}}, \end{aligned}$$

(17)

$$\begin{aligned} g_{\mathcal {D}^{*} \mathcal {D}^{*} \mathcal {P}}= & {} \frac{g_{\mathcal{D}^{*} {\mathcal D} {\mathcal {P}}}}{\sqrt{m_{\mathcal {D}} m_{\mathcal {D}^{*}}}} , \end{aligned}$$

(18)

with $g_V = {m_\rho / f_\pi }$ and $f_\pi = 132$ MeV [27], $\beta =0.9$, $\lambda = 0.56 \, \mathrm{GeV}^{-1}$ and $g=0.59$ [53].

3.1 $\chi '_{c1} \rightarrow VV$

The X(3872) resonance has the same quantum numbers as $\chi _{c1}^{\prime }$ but with a much lighter mass than the one predicted by potential quark model. Hence, we study the partial decay widths of the $\chi '_{c1} \rightarrow VV$ as a function of the mass of $\chi _{c1}^\prime$ from 3.8 to 4.0 GeV, which covers the predicted values of the quark models [51, 54, 55].

In Fig. 3a, we plot the partial widths of $\chi _{c1}^{\prime } \rightarrow \omega \omega$ (solid line) and $\rho \rho$ (dashed line) in terms of the mass of $\chi _{c1}^\prime$ with $\alpha =0.2$, respectively. From Fig. 3a, one can see that the calculated partial widths are sensitive to the mass of $\chi _{c1}^\prime$, which can vary from order of keV to order of MeV. Since these two decay modes have the same intermediate charmed meson loops as shown in Fig. 1, they have the similar behavior as a function of the mass of $\chi '_{c1}$. In Fig. 3b, we show the partial widths of $\chi '_{c1} \rightarrow K^{*0} {\bar{K}}^{*0}$ (solid line) and $K^{*+} K^{*-}$ (dashed line). For $\chi '_{c1} \rightarrow K^{*0} {\bar{K}}^{*0}$, the transition is via $[D^+D^{*-}]D_s^{(*)}$ intermediate mesons in Fig. 1, which leads to an enhancement at the $D^+D^{*-}$ threshold. Similarly, the $\chi '_{c1} \rightarrow K^{*+} K^{*-}$ transition is via $[D^0 {\bar{D}}^{*0}]D_s^{(*)}$ intermediate mesons, which leads to an enhancement at the $D^0 {\bar{D}}^{*0}$ threshold. In Fig. 3c, we show our numerical results for $\chi _{c1}^\prime \rightarrow \phi \phi$ decay, where there is no cusp structure. This is because the mass range of $\chi _{c1}^\prime$ lies below the intermediate $D_s^*{\bar{D}}_s^*$ threshold. The calculated partial widths of $\chi _{c1}^\prime \rightarrow \phi \phi$ is about $3 \sim 4$ orders smaller than that of other decay modes in Fig. 3a, b. It indicates the threshold effects via strange charmed meson pair is less important in $\chi _{c1}^\prime \rightarrow \phi \phi$.

Fig. 3

$m_{\chi _{c1}^\prime }$-dependence of the decay width of $\chi _{c1}^\prime \rightarrow VV$ with $\alpha =0.2$

Next, we consider the form factors effects on the partial decay widths with different cutoff parameters $\alpha$. In Fig. 4, the partial decay widths of $\chi _{c1}^\prime \rightarrow VV$ are plotted in terms of $\alpha =0.2\sim 0.4$, and we take the mass of $\chi _{c1}^\prime = 3.872$ GeV. One can see that the partial width of $\chi _{c1}^\prime \rightarrow \phi \phi$ is about $2\sim 4$ orders smaller than the ones of other decay modes at the same value of $\alpha$, which indicates that contribution of the intermediate charmed meson loop to the process of $\chi _{c1}^\prime \rightarrow \phi \phi$ is much smaller than the ones to other channels. This is easily to be understand, since the mass of $\chi _{c1}^\prime$ is much far away from the mass threshold of $D_s D_s^*$ than $DD^*$.

Furthermore, the total width of the X(3872) is smaller than 1.2 MeV as quoted in the PDG [39]. Some theoretical works [56,57,58] suggest that the width of X(3872) should be less than 100 keV based on the molecule ansatz of X(3872). The numerical results here as shown in Fig. 4 are larger than the above upper limits of X(3872), which illustrate from the other side that the X(3872) is at least not pure $c\bar{c}$ charmonium state, or there is only small $c\bar{c}$ component in its wave function. We expect that the more and precise experimental measurements on the relevant channels can help us improving our understanding about the nature of the X(3872) state.

Fig. 4

$\alpha$-dependence of the decay width of $\chi _{c1}^{\prime }\rightarrow VV$ with the $m_{\chi _{c1}^{\prime }}=3.872$ GeV

3.2 $\chi '_{c2} \rightarrow VP$

The X(3930) was observed in the $\gamma \gamma \rightarrow D\bar{D}$ process by Belle [59] and Babar [60] collaborations, and has been a good candidate for the $\chi _{c2}^{\prime }$ state. The accessible decay modes are only $\chi _{c2}^{\prime } \rightarrow K^*\bar{K} +c.c$ and $\rho ^+\pi ^- +c.c$ due to C-parity conservation. In Table 1, we present the calculated partial widths of $\chi _{c2}^{\prime }$ for each channel with cutoff parameters $\alpha =0.4$, 0.6, and 0.8, respectively. As can be seen in Table 1, the partial widths of $\chi _{c2}^{\prime }\rightarrow K^*\bar{K}+c.c$ turn out to be sizeable, while the partial widths of $\chi _{c2}^{\prime } \rightarrow \rho ^+\pi ^- +c.c$ is found to be much smaller than the $K^*\bar{K}+c.c$ channel. This is because of the U-spin symmetry breaking caused by u/d and s quark mass difference in $K^*\bar{K}+c.c$ channel is much larger than the isospin symmetry breaking caused by u and d quark mass difference in $\rho \pi$ channel. If we take the $\chi _{c2}^{\prime }$ total width $\Gamma _\mathrm{total}= 24$ MeV from PDG [39], with the $\alpha =0.4 \sim 0.8$, the lower and upper bounds of $\mathrm{BR}(\chi _{c2}^{\prime } \rightarrow K^* K +c.c)$ are about $1.25\times 10^{-3}$ and $1.9\%$, respectively. The lower and upper bounds of $\mathrm{BR}(\chi _{c2}^{\prime } \rightarrow \rho ^+\pi ^- +c.c)$ are about $2.67\times 10^{-5}$ and $3.03\times 10^{-4}$, respectively.

Table 1 The partial widths (in units of keV) of $\chi _{c2}^\prime \rightarrow VP$ with different $\alpha$ values. We take the mass of $\chi '_{c2}$ is 3927.2 MeV as in PDG [39]

In Fig. 5, we plot the form factor parameter $\alpha$ dependence of the decay widths of $\chi _{c2}^{\prime }\rightarrow VP$ with $m_{\chi '_{c2}} = 3927.2$ MeV. In this work, we take a relative smaller $\alpha$ range, between 0.4 and 0.8, which is acceptable since the form factors for the off-shell effects arising from the three intermediate mesons, instead of only the right exchanged meson in the triangle loop.

Fig. 5

$\alpha$-dependence of the decay width of $\chi _{c2}^{\prime }\rightarrow VP$ with $m_{\chi _{c2}^{\prime }}=3.930$ GeV

Fig. 6

The $\alpha$-dependence of the ratios defined in Eq. (19) with $m_{\chi _{c1}^{\prime }}=3.872$ GeV

Fig. 7

The $\alpha$-dependence of the ratios defined in Eq. (20) with $m_{\chi _{c2}^{\prime }}=3.930$ GeV

In general we cannot provide the value of the cutoff parameter $\alpha$, which should be determined by the experimental measurements. But, it would be interesting to further clarify the uncertainties arising from the introduction of form factors by studying the cutoff parameter $\alpha$ dependence of the ratios between different partial decay. For doing this, we next study the ratios of different partial decay widths, where the effects of the couplings of the vertices are canceled, and these ratios only reflects the open threshold effects through the intermediate charmed meson loops. For the decays of $\chi _{c1}^\prime \rightarrow VV$, we define the following ratios:

$$\begin{aligned} R_1= & {} \frac{\Gamma (\chi _{c1}^\prime \rightarrow K^{*0} {\bar{K}}^{*0})}{\Gamma (\chi _{c1}^\prime \rightarrow \rho \rho )} \, , \nonumber \\ R_2= & {} \frac{\Gamma (\chi _{c1}^\prime \rightarrow K^{*+} K^{*-})}{\Gamma (\chi _{c1}^\prime \rightarrow \rho \rho )} \, , \nonumber \\ R_3= & {} \frac{\Gamma (\chi _{c1}^\prime \rightarrow \omega \omega )}{\Gamma (\chi _{c1}^\prime \rightarrow \rho \rho )} \, , \nonumber \\ R_4= & {} \frac{\Gamma (\chi _{c1}^\prime \rightarrow \phi \phi )}{\Gamma (\chi _{c1}^\prime \rightarrow \rho \rho )} \, , \end{aligned}$$

(19)

and, for $\chi _{c2}^\prime \rightarrow VP$, we define,

$$\begin{aligned} r_1= & {} \frac{\Gamma (\chi _{c2}^\prime \rightarrow K^{*+} K^- +c.c.)}{\Gamma (\chi _{c2}^\prime \rightarrow \rho ^+\pi ^-)} \, , \nonumber \\ r_2= & {} \frac{\Gamma (\chi _{c2}^\prime \rightarrow K^{*0} {\bar{K}}^{0}+c.c.)}{\Gamma (\chi _{c2}^\prime \rightarrow \rho ^+\pi ^-)} \, . \end{aligned}$$

(20)

We show the numerical results for these ratios of Eqs. (19) and (20) in Figs. 6 and 7 as a function of the cutoff parameter $\alpha$, from where we see that the dependence of these ratios on the cutoff parameter $\alpha$ is rather weak, which shows the validity of our model. These numerical results can be tested by the experimental measurements in future.

4 Summary

In this work, we have investigated the charmless decays $\chi _{c1}^\prime \rightarrow VV$ and $\chi _{c2}^\prime \rightarrow VP$ via IML, which are supposed to be suppressed by HSR in pQCD. Applying an effective Lagrangian approach, the charmed meson loop contributions are calculated for evading HSR. We determined the cutoff parameter $\alpha$ values for $\chi _{c1} \rightarrow VV$ and $\chi _{c2} \rightarrow VP$ by reproducing the experimental data, which guide us to determine the cutoff $\alpha$ range in $\chi _{c1}^\prime \rightarrow VV$ and $\chi _{c2}^\prime \rightarrow VP$. Our results have shown that the intermediate charmed meson loops may play an important role in these processes, especially when the initial states are close to the two particle thresholds.

For $\chi _{c1}^\prime \rightarrow VV$, the partial widths of $\rho \rho$, $\omega \omega$, and $K^*{\bar{K}}^*$ channels can reach to order of MeV, while partial widths of $\phi \phi$ channel can only reach to order of keV. For $\chi _{c2}^\prime \rightarrow VP$, the partial widths of $\chi _{c2}^{\prime }\rightarrow K^*\bar{K}+c.c$ turns out to be sizeable, while the partial widths of $\chi _{c2}^{\prime } \rightarrow \rho ^+\pi ^- +c.c$ is found to be much smaller than the $K^*\bar{K}+c.c$ channel. This is because of the U-spin symmetry breaking caused by $u/d-s$ quark mass difference in $K^*\bar{K}+c.c$ channel is much larger than the isospin symmetry breaking caused by $u-d$ quark mass difference in $\rho \pi$ channel. Our calculations may be examined by the future BESIII experiments.