Abstract
This paper develops a new solution of gravitational vacuum star in the background of charged Kiselev black holes as an exterior manifold. We explore physical features and stability of thin-shell gravastars with radial perturbation. The matter thin layer located at thin-shell greatly affects stable configuration of the developed structure. We assume three different choices of matter distribution such as barotropic, generalized Chaplygin gas and generalized phantomlike equation of state. The last two models depend on the shell radius, also known as variable equation of state. For barotropic model, the structure of thin-shell gravastar is mostly unstable while it shows stable configuration for such type of matter distribution with extraordinary quintessence parameter. The resulting gravastar structure indicates stable behavior for generalized Chaplygin gas but unstable for generalized phantomlike model. It is also found that proper length, entropy and energy within the shell show linear relation with thickness of the shell.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The study of final outcomes of gravitational collapse is an interesting topic that explores the formation of various compact objects such as white dwarfs, neutron stars, naked singularities and black holes (BHs). The collapse end-state is a widely accepted research field from many perspectives, both theoretical and observational. The classical tgeneral relativity faces some major scientific issues precisely related to the paradoxical characteristics of BHs and naked singularities. An astronomical substance hypothesized as a substitute for the BH is a gravastar (gravitational vacuum star) based on the idea of Mazur’s and Motola’s theory [1, 2]. The basic idea is to prevent the formation of event horizons and singularities by stopping the collapse of matter at or near the position of event horizon. A gravastar appears similar to a black hole but does not contain event horizon and singularity.
Gravastars are of purely theoretical interest and can be described in three different regions with the specific equation of state (EoS). The first region is referred to as an interior (\(0\le r<r_1\)), second is the intermediate (\(r_1< r<r_2\)) and third is denoted as an exterior region (\(r_2<r\)). In the first region, the isotropic pressure (\(p=-\sigma \), where \(\sigma \) represents the energy density) produces a repulsive force on the intermediate thin-shell. It is assumed that the intermediate thin-shell is protected by ultrarelativistic plasma and fluid pressure (\(p=\sigma \)). The exterior region has zero pressure (\(p=0=\sigma \)) and can be supported by the vacuum solution of the field equations. It contains a stable thermodynamic solution and maximum entropy for small fluctuations. Visser’s cut and paste method provides a general formalism for the construction of thin-shell from the joining of two different spacetimes at hypersurface [3]. Mazur and Mottola [2] considered this approach to construct thin-shell gravastar from the matching of exterior Schwarzschild BH with interior de Sitter (DS) spacetime. This approach is very useful to avoid the presence of event horizon as well as central singularity in the geometry of gravastars.
The matter surface at thin-shell creates a sufficient amount of pressure to overcome the force of gravity effects that help to maintain its stable configuration. For the description of Mazur–Mottola scenario, Visser and Wiltshire [4] introduced the simplest model from the matching of exterior and interior geometries through the cut and paste approach. They also analyzed stable configuration of the developed structure for suitable choice of EoS for the transition layers. Carter [5] extended this concept by the joining of interior DS spacetime and exterior Reissner–Nordström (RN) BH. They examined the effects of EoS on the modeling of thin-shell gravastars. Horvat et al. [6] presented theoretical model of gravastars with electromagnetic field and studied the role of charge on the stable configuration of gravastars. Rahaman et al. [7, 8] studied physical features like proper length, entropy and energy contents of charged and charged free thin-shell gravastars in the background of (2+1)-dimensional spacetime. They claimed that the presented solutions are non-singular and physically viable as an alternative to BH. Banerjee et al. [9] investigated the braneworld thin-shell gravastars developed by using braneworld BH as an exterior manifold through cut and paste technique.
Rocha et al. [10,11,12] discussed stable configuration of thin-shell gravastars with perfect fluid distribution in Vaidya exterior spacetime. They proposed a dynamical model of prototype gravastars filled with phantom energy. It is found that the developed structure can be a BH, stable, unstable or “bounded excursion” gravastar for various matter distributions at thin-shell. Horvat et al. [13] studied the geometry of gravastars with continuous pressure by using the conventional Chandrasekhar approach and derived EoS for the static case. Lobo and Garattini [14] investigated the stability of noncommutative thin-shell gravastar and found that stable regions must exist near the expected position of the event horizon. Övgün et al. [15] developed thin-shell gravastar model from the matching of exterior charged noncommutative BH with interior DS manifold. They found that the developed structure follows the null energy condition and shows stable behavior for some suitable values of physical parameter near the expected event horizon. Recently, we have developed regular thin-shell gravastars in the background of Bardeen/Bardeen DS BHs as exterior manifolds through cut and paste method [16]. The stable configuration of the developed structure is explored through radial perturbation. It is found that stable regions decrease for large values of charge and increase for higher values of the cosmological constant.
The theoretical modeling of gravastar could be helpful for the better understanding of dark energy role in the accelerated expanding behavior of the universe. Ghosh et al. [17] examined physical characteristics of gravastar model with Kuchowicz metric potential. They claimed that this model overcomes the singularity problems that occurred for the geometry of BH in general relativity. Shamir and Ahmad [18] investigated physical features of gravastar model in the background of f(G, T) gravity. Yousaf et al. [19] explored stable configuration of charged gravastar filled with isotropic fluid in f(R, T) gravity. They found linear relation among the physical features and thickness of the shell. Sharif and Waseem [20] discussed charged gravastars with conformal motion in f(R, T) gravity. There is a large body of literature [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40] that explore the stable as well as dynamical configuration of thin-shell wormholes constructed from the matching various BHs with different EoS.
This paper presents the formalism of charged Kiselev thin-shell gravastars to explore stable configuration with different EoS. The paper has the following format. Section 2 explains the formalism of thin-shell gravastars in the background of charged Kiselev BH. In Sect. 3, we study the effects of barotropic and variable EoS on the stable configuration of the developed structure through radial perturbation. Finally, we summarize our results in the last section.
2 Gravastars formalism
This section explores the geometrical construction of thin-shell gravstars from the joining of lower (\(\Upsilon ^-\)) and upper (\(\Upsilon ^+\)) manifolds through cut and paste technique. For this purpose, we consider DS spacetime as a lower manifold and charged BH surrounded by the quintessence matter as an upper manifold. The motivation behind the consideration of this model can be explained as follows. The matter with negative pressure can be characterized for the current evolutionary phase of the universe with cosmological constant and quintessence [41]. The mathematical representation of quintessence matter distribution that linear relates energy density (\(\sigma _q\)) and pressure (\(p_q\)) is \(p_q=w\sigma _q\), where \(\omega \) denotes the quintessence parameter. This parameter explains that the universe is in the phase of accelerated expansion if \(-1<\omega <-1/3\), decelerates if \(\omega >-1/3\) and shows inertial behavior (constant expansion rate) if \(\omega =-1/3\). This means that observers must have future horizons in all accelerated models [42]. In an accelerated expanding universe, two objects separated with a relative fixed distance r must achieve relative speed to the speed of light after some time and will no longer communicate. For the case of decelerated expansion, the breakdown of such a communication does not happen whereas it becomes less relativistic with time. However, the speed of relative moving observers must be constant for the case of \(\omega =-1/3\). They can communicate but cannot maintain this forever as they recede away from each other.
Kiselev [43] introduced uncharged and charged BH surrounded by the quintessence matter distribution as a static spherically symmetric solution of the field equations. The line element of charged Kiselev BH is given as
where
m is the mass of BH, Q denotes the charge of BH, \(\alpha \) stands for the Kiselev parameter and \(\omega \) is the quintessence parameter with \(-1<\omega <-1/3\). The boundary values of EoS parameter recover the case of cosmological constant (extraordinary quintessence) for \(\omega =-1\) and \(\omega =0\) is referred to as the dust fluid. If \(Q=0\), then it reduces to Kiselev BH and RN BH is recovered when Kiselev parameter vanishes. The charged Kiselev BH reduces to Schwarzschild BH in the absence of both charge and Kiselev parameter. The corresponding metric function of Kiselev BH has the following form
Extreme BHs are expected to have both stable and unstable properties, this makes their analysis very interesting and challenging. We consider \(\omega =-2/3\in (-1,-1/3)\) to observe the event horizon of Kiselev BH. The corresponding event horizons are given as
It is found that
-
for \(\alpha =1/8m\), it denotes extreme Kiselev BH,
-
for \(\alpha <1/8m\), it represents the non-extreme Kiselev BH,
-
for \(\alpha >1/8m\), it shows naked singularity.
Since the charged Kiselev BH metric function is much complicated than RN and Kiselev BH, so its event horizon for \(\omega =-2/3\) has much complicated expression. Thus we only discuss values of the parameter for which it shows different geometrical structure. It follows that
-
for \(Q^2=\frac{2}{27\alpha ^2}\left( -2+18m\alpha -2(1-6m\alpha )^{3/2}\right) \), it denotes extreme charged Kiselev BH,
-
for \(Q^2>\frac{2}{27\alpha ^2}\left( -2+18m\alpha -2(1-6m\alpha )^{3/2}\right) \), it represents the non-extreme charged Kiselev BH,
-
for \(Q^2<\frac{2}{27\alpha ^2}\left( -2+18m\alpha -2(1-6m\alpha )^{3/2}\right) \), it shows naked singularity.
The line element of DS geometry is given as
where \(\Phi (r_{-})=1-r^2_-/\beta ^2\) and \(\beta \) is a nonzero positive constant. We use cut and paste method to obtain the geometry of thin-shell gravastars from the matching of two distinct spacetimes \(\Upsilon ^-\) and \(\Upsilon ^+\). These manifolds have the metric functions defined by \(g^{\pm }_{\mu \nu }(x_{\pm }^\mu )\) with independent coordinates \(x_{\pm }^\mu \) and bounded by the hypersurfaces \(\partial \Upsilon ^{\pm }\) with induced metrics \(h_{ij}^{\pm }\), respectively. According to the Darmoise junction conditions, the induced metrics are isometric and follow the relation \(h_{ij}^{+}(\xi ^i)=h_{ij}(\xi ^i) =h_{ij}^{-}(\xi ^i)\), where \(\xi ^i\) represents the coordinates of \(\partial \Upsilon ^{\pm }\). These geometries are glued at the hypersurface to obtain the single manifold \(\Upsilon =\Upsilon ^+\cup \Upsilon ^-\) with boundary \(\partial \Upsilon =\partial \Upsilon ^+=\partial \Upsilon ^-\). Mathematically, these spacetimes can be described as
where \(\tau \) and \(b(\tau )\) denote the proper time and radius of thin-shell. The corresponding hypersurface that linked these geometries can be parameterized as
The induced 3D metric at hypersurface \((h_{ij})\) can be expressed as
where \(\xi ^{i}=(\tau ,\theta ,\phi )\). The normal vector components of \(g_{\mu \nu }\) on the \(\partial \Upsilon \) are defined as
where \(f(r,b(\tau ))=r-b(\tau )=0\) represents the function of \(\partial \Upsilon \) and \(b(\tau )=b\) denotes the shell’s radius. The components of normal vectors corresponding to upper and lower spacetimes are
respectively. Here, dot represents derivative with respect to \(\tau \). The normal vector satisfies the condition \(n^\mu n_\mu =1\) for spherical symmetric manifolds. The discontinuity in the second fundamental form (extrinsic curvature) exist due to the presence of matter surface at \(\partial \Upsilon \). The extrinsic curvature components for both geometries are
The matter surface at thin-shell produces discontinuity in the extrinsic curvatures of both spacetimes. If \(K_{ij}^{+}-K_{ij}^{-}\ne 0\), then it represents the presence of matter thin layer on \(\partial \Upsilon \). The components of energy-momentum tensor (\(S^{i}_{j}\)) of such a matter surface are determined by the Lanczos equations. Mathematically, it can be expressed as
where \([K^{i}_{j}]=K^{+i}_{j}-K^{-i}_{j}\) and \(K=tr[K_{ij}]=[K^{i}_{j}]\). The above equation in terms of perfect fluid distribution becomes
here \(v_i\) denotes thin-shell velocity components. By considering Eqs. (5)–(11), we obtain \(\sigma \) and p in the following form
Here, we assume that \(\dot{b}_{0}=\ddot{b}_{0}=0\), where \(b_0\) is the position of equilibrium shell’s radius. This shows that shell’s motion along the radial direction vanishes at \(b=b_0\). The respective expressions for surface stresses at \(b=b_0\) yield
The continuity of perfect fluid gives the relationship between the surface stresses of thin-shell gravastars as
which can be expressed as
The second order derivative of \(\sigma \) with respect to b yields
where \(\varsigma ^2=dp/d\sigma \) denotes the EoS parameter. Equations (16)–(18) are very useful to explore the dynamics and stable configurations of constructed geometry with different types of matter distribution.
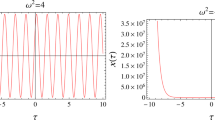
For the physical viability of a geometrical structure, some constraints must be imposed known as energy conditions. The well-known energy conditions are null: \(\sigma _0+p_0>0\); weak: \(\sigma _0>0\), \(\sigma _0+p_0>0\); strong: \(\sigma _0+3p_0>0\), \(\sigma _0+p_0>0\); dominant: \(\sigma _0>0\), \(\sigma _0\pm p_0>0\). If these energy conditions are verified then the developed model is physically viable. Here, we are interested to check the null energy condition that ensure the presence of normal or exotic matter at thin-shell. It is interesting to mention here that the violation of the null energy condition leads to the violation of remaining conditions. We see that thin-shell gravastars follow the null energy condition for different values of charge and mass of BH as shown in Fig. 1. These values of physical parameters have frequently been used in literature that examine the stable as well as dynamical behavior of thin-shell constructed from different singular and non-singular BHs [24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40]. Thus we use them to determine the effects of charge and mass on the energy conditions, physical features as well as stability of thin-shell gravastars (see Appendix A).
3 Stability analysis
This section studies stability of thin-shell gravastars using linear perturbation in the radial direction at \(b=b_0\) with different variable EoS. The stable and unstable configurations of thin-shell gravastars can be analyzed through the behavior of effective potential of thin-shell. The equation of motion of thin-shell that explains the stable as well as dynamical characteristics of respective geometry is obtained directly from Eq. (12) as
here \(\Omega (b)\) denotes the potential function of thin-shell gravastar as
where
The stable behavior of thin-shell gravastars is studied by using second derivative of the effective potential at \(b=b_0\). The basic conditions for the stable behavior can be written as \(\Omega (b_0)=0=\Omega '(b_0)\) and \(\Omega ''(b_0)>0\). If \(\Omega ''(b_{0})<0\), then it shows unstable behavior and it is unpredictable if \(\Omega ''(b_{0})=0\) [30]. To check the stability through radial perturbation, we linearize the potential function using Taylor series expansion around equilibrium radius \(b_0\) as follows
We examine that \(\Omega (b_0)=0=\Omega '(b_0)\), hence it reduces to
The corresponding second derivative of \(\Omega (b)\) at \(b=b_0\) becomes
where \(M(b_0)=4\pi b_0^2 \sigma _0\) denotes the total mass distribution at equilibrium shell’s radius. The corresponding first and second derivatives of the total mass with respect to b at \(b=b_0\) become
and \(\varsigma _0^2=dp/d\sigma |_{b=b_0}\).
Firstly, we begin with barotropic EoS to discuss the stability of the developed geometry. It gives linear relation between the surface stresses of thin-shell as \(p=\gamma \sigma \) with real constant \(\gamma \). Consequently, the solution of conservation equation (17) for barotropic EoS is given as
The corresponding potential function becomes
which turns out to be zero at throat radius \(b=b_0\). The corresponding first derivative of \(\Omega (b)\) yields
which vanishes only if
The second derivative of \(\Omega (b)\) at \(b=b_0\) yields
This equation explains stable and unstable configurations of thin-shell gravastars for barotropic EoS. Due to complexity of this expression, we use numerical approach to observe the effects of physical parameters on the stability of developed structure. We study the graphical behavior of \(\Omega ''(b_{0})\) by using Eqs. (26) and (14). It is found that stable structure of thin-shell is greatly affected by the presence of quintessence EoS parameter. We examine that thin-shell expresses unstable behavior for every values of Q, m, \(\alpha \) and \(\beta \) with \(\omega =-2/3\) as shown in the left plot of Fig. 2. We obtain unstable configuration for every choice of \(\omega \) except for extraordinary quintessence parameter \(\omega =-1\) (right plot of Fig. 2). Hence, the barotropic type fluid distribution at thin-shell shows stable behavior only for \(\omega =-1\) otherwise gives unstable solutions.
Current observational data seem to point towards an accelerated expansion of the universe [44,45,46]. If general relativity is assumed to be correct theory of gravity describing the large-scale behavior of the universe, then its energy density and pressure should violate the strong energy condition. Several models for the matter leading to such a situation have been proposed [47,48,49]. One of them is the Chaplygin gas [50,51,52], a perfect fluid satisfying the EoS \(p \sigma = \eta \), where \(\eta <0\). A remarkable property of the Chaplygin gas is that the squared sound velocity \(v_s^2=\eta /\sigma ^2\) is always positive even in the case of exotic matter. Varela [21] considered the EoS of the type \(p=p(\sigma ,b)\) to discuss the stability of thin-shell wormhole developed from two equivalent copies of the Schwarzschild BH. Such type of EoS is known as variable EoS. The generalized form of the Chaplygin gas presents the mathematical formulation in which surface pressure depends on the radius of the shell.
Therefore, we consider general form of Chaplygin EoS (\(p=p(\sigma ,b)\)) to study the stable behavior of the respective geometry, i.e., \(p=\frac{1}{b^n}\frac{\eta }{\sigma }\) with real constants \(\eta <0\) and n [21]. It is observed that the Chaplygin gas model is recovered for \(n=0\) [53]. The respective solution of conservation equation for such a model can be written as
The effective potential for this model turns out to be
It is observed that \(\Omega (b_0)=0\) and \(\Omega '(b_0)\) becomes
For \(\Omega '(b_0)=0\), we have
Consequently, \(\Omega ''(b_0)\) has the following form
Now, we observe the effects of the generalized Chaplygin gas EoS on the stability of developed geometry. In this regard, we observe the graphical behavior of \(\Omega ''(b_0)\) for this model. It is found that thin-shell expresses stable behavior for every choice of the physical parameters except \(\omega =-1\) when \(n=0\) (Fig. 3). This shows that thin-shell becomes stable for the choice of Chaplygin gas model (\(n=0\)) and represents unstable behavior only for \(\omega =-1\) (left plot of Fig. 4). It is also analyzed that the general case of Chaplygen EoS (\(n\ne 0\)) shows stable behavior for every choice of \(\omega \) with \(n=1\) (right plot of Fig. 4). We see that stable behavior (\(\Omega ''(b_0)>0\)) increases for higher values of n as shown in Fig. 5.
Finally, we study the effects of generalized phantomlike variable EoS on the stability of thin-shell [21] whose EoS is \(p=\frac{\Theta \sigma }{b^n}\) with real constants \(\Theta \) and n. The phantomlike EoS is recovered if \(n=0\) [54]. By using this expression in Eq.(17), we have
and it follows that
It is noted that \(\Omega (b_0)=0\) and by considering \(\Omega '(b_0)=0\), we obtain
and hence
For the general form of phantomlike EoS, we see that thin-shell shows initially stable behavior then expresses unstable configuration for every choice of physical parameters (Figs. 6 and 7). We conclude that the constructed geometry is neither stable nor unstable completely for the choice of both phantomlike and general form of phantomlike EoS.
4 Final remarks
This paper investigates the construction of thin-shell gravastars from the matching of two different spacetimes, i.e., DS as a lower spacetime and charged Kiselev BH as an upper manifold. These geometries are connected through the well-known cut and paste method. We match these manifolds at \(r=b\) with \(b>r_h\) to avoid the presence of event horizon (\(r_h\)) and singularity in the developed structure. The presence of matter thin layer at the joining surface produces discontinuity in the extrinsic curvature. It is found that the null energy condition is verified for the developed structure (Fig. 1). We have studied stable characteristics of thin-shell gravastars with barotropic type fluid distribution and two variable EoS, i.e., generalized Chaplygin gas and phantomlike EoS.
For barotropic model, we have obtained stable solution for the choice of \(\omega =-1\) and unstable solution for any other choice of \(\omega \) (Fig. 2). It is interesting to mention here that this model mostly indicates unstable behavior for thin-shell WHs in several spacetimes [21,22,23, 37,38,39,40]. These results express that the stable solution can be obtained through barotropic model for some suitable choice of physical parameters. The stable structure is obtained for Chaplygin gas model (\(n=0\)) for every choice of \(\omega \) other than extraordinary quintessence parameter \(\omega =-1\). For generalized Chaplygin gas EoS, we have obtained stable solution for every values of physical parameter and found more stable structure for higher values of n (Figs. 3, 4, 5). Finally, for generalized phantomlike EoS, thin-shell shows initially stable behavior and then expresses unstable configuration for every choice of the physical parameters (Figs. 6 and 7).
We conclude that charged Kiselev thin-shell gravastars are more stable for the choice of generalized Chaplygin gas model. It is worthwhile to mention here that this model is more stable with considered EoS than thin-shell WHs in the background of various BHs [21,22,23, 37,38,39,40]. This shows completely stable structure of thin-shell gravastar with extraordinary quintessence parameter for both barotropic and generalized Chaplygin gas model.
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: We have not used any observational data in this paper. Consequently, no data will be deposited.]
References
P. Mazur, E. Mottola, Report No. LA-UR-01- 5067 arXiv:gr-qc/0109035
P. Mazur, E. Mottola, Proc. Natl. Acad. Sci. 101, 9545 (2004)
M. Visser, S. Kar, N. Dadhich, Phys. Rev. Lett. 90, 201102 (2003)
M. Visser, D.L. Wiltshire, Class. Quantum Gravity 21, 1135 (2004)
B.M.N. Carter, Class. Quantum Gravity 22, 4551 (2005)
D. Horvat, S. Sasa Ilijic, A. Marunovic, Class. Quantum Gravity 26, 025003 (2009)
F. Rahaman, A.A. Usmani, S. Ray, S. Islam, Phys. Lett. B 707, 319 (2012)
F. Rahaman, A.A. Usmani, S. Ray, S. Islam, ibid 717, 1 (2012)
A. Banerjee, F. Rahaman, S. Islam, M. Govender, Eur. Phys. J. C 76, 34 (2016)
P. Rocha, R. Chan, M.F.A. da Silva, A. Wang, J. Cosmol. Astropart. Phys. 2008, 10 (2008)
P. Rocha, R. Chan, M.F.A. da Silva, A. Wang, ibid 2009, 10 (2009)
P. Rocha, R. Chan, M.F.A. da Silva, A. Wang, ibid 2011, 13 (2011)
D. Horvat, S. Ilijic, A. Marunovic, Class. Quantum Gravity 28, 195008 (2011)
F.S.N. Lobo, R. Garattini, J. High Energy Phys. 1312, 065 (2013)
A. Övgün, A. Banerjee, K. Jusufi, Eur. Phys. J. C 77, 566 (2017)
M, Sharif, F. Javed, F https://doi.org/10.1016/j.aop.2020.168124
S. Ghosh, F. Rahaman, B.K. Guha, S. Ray, Phys. Lett. B 767, 380 (2017)
M.F. Shamir, M. Ahmad, Phys. Rev. D 97, 104031 (2018)
Z. Yousaf et al., Phys. Rev. D 100, 024062 (2019)
M. Sharif, A. Waseem, Astrophys. Space Sci. 364, 189 (2019)
V. Varela, Phys. Rev. D 92, 044002 (2015)
M. Sharif, F. Javed, Gen. Relativ. Gravit. 48, 158 (2016)
M. Sharif, F. Javed, Astrophys. Space Sci. 364, 179 (2019)
D. Núñez, H. Quevedo, M. Salgado, Phys. Rev. D 58, 083506 (1998)
S.H. Mazharimousavi, M. Halilsoy, Z. Amirabi, Phys. Rev. D 81, 104002 (2010)
F. Rahaman, S. Ray, A.K. Jafry, K. Chakraborty, Phys. Rev. D 82, 104055 (2010)
G.A.S. Dias, J.P.S. Lemos, Phys. Rev. D 82, 084023 (2010)
M. Sharif, G. Abbas, Gen. Relativ. Gravit. 43, 1179 (2011)
M. Sharif, M. Azam, Eur. Phys. J. C 73, 2407 (2013)
F. Rahaman, A. Banerjee, I. Radinschi, Int. J. Theor. Phys. 52, 2943 (2013)
M. Sharif, S. Iftikhar, Astrophys. Space Sci. 356, 89 (2015)
S.D. Forghani, S. Habib Mazharimousavi, M. Halilsoy, Eur. Phys. J. C 78, 469 (2018)
M. Sharif, F. Javed, Int. J. Mod. Phys. D 28, 1950046 (2019)
M. Sharif, F. Javed, Ann. Phys. 407, 198 (2019)
M. Sharif, F. Javed, Mod. Phys. Lett. A 35, 1950350 (2019)
M. Sharif, F. Javed, Chin. J. Phys. 61, 262 (2019)
P.K.F. Kuhfittig, Turk. J. Phys. 43, 213 (2019)
M. Sharif, F. Javed, Int. J. Mod. Phys. D 29, 2050007 (2020). https://doi.org/10.1142/S0217751X20400151
M. Sharif, F. Javed, Int. J. Mod. Phys. A 35, 2050030 (2020). https://doi.org/10.1016/j.aop.2020.168146
M. Sharif, F. Javed, M. Sharif, F. Javed https://doi.org/10.1142/S0217732320503095
S. et al.: Astrophys. J. 517(1999)565
S. Hellerman, N. Kaloper, L. Susskind, J. High Energy Phys. 6, 3 (2001)
V.V. Kiselev, Class. Quantum Gravity 20, 1187 (2003)
A. Riess et al., Astron. J. 116, 1009 (1998)
S.J. Perlmutter et al., Astroph. J. 517, 565 (1999)
N.A. Bahcall et al., Science 284, 1481 (1999)
V. Sahni, A.A. Starobinsky, Int. J. Mod. Phys. A 9, 373 (2000)
P.J. Peebles, B. Ratra, Rev. Mod. Phys. 75, 559 (2003)
T. Padmanabhan, Phys. Rep. 380, 235 (2003)
A. Kamenshchik, U. Moschella, V. Pasquier, Phys. Lett. B 511, 265 (2001)
N. Bilic, G.B. Tupper, R.D. Viollier, Phys. Lett. B 535, 17 (2002)
M.C. Bento, O. Bertolami, A.A. Sen, Phys. Rev. D 66, 043507 (2002)
E.F. Eiroa, C. Simeone, Phys. Rev. D 76, 024021 (2007)
P.K.F. Kuhfittig, Acta Phys. Polon. B 41, 2017 (2010)
Acknowledgements
One of us (FJ) would like to thank the Higher Education Commission, Islamabad, for its financial support through 6748/Punjab/NRPU/RD/HEC/2016.
Author information
Authors and Affiliations
Corresponding author
Appendix A
Appendix A
We also explore some physical features of the developed structure, i.e., proper length, entropy and energy contents within the shell’s region. Since the constructed geometry is the matching of two different spacetimes, so the stiff perfect fluid moves along these spacetimes through the shell region. The lower and upper boundaries of the shell are \(r=b\) and \(r=b+\epsilon \), respectively. The proper thickness of the shell is denoted by \(\varepsilon \) which is a very small positive real number (\(0<\varepsilon \ll 1\)). The proper thickness of such a region that connects lower and upper spacetimes can be obtained as [17]
This integral cannot be solved analytically due to the complicated expression of \(\Psi (r)\). Therefore, we solve it by assuming \(\sqrt{\Psi ^{-1}_{+}(r)}=\frac{dj(r)}{dr}\) as
where \(\epsilon \ll 1\) so that its square and higher powers can be neglected. The corresponding expression for proper length becomes
It is noted that the proper length of the shell clearly depends on the charge as well as the mass of the BH. Equation (38) shows that the proper length and thickness of the shell are proportional. It is found that the length of the shell decreases by an increasing charge of the geometry and increases by increasing the mass of the BH.
Entropy is related to the measure of disorderness or disturbance in a geometrical structure. We study the entropy of thin-shell gravastars that explains the disorderness in the geometry of gravastar. According to the theory of Mazur and Mottola, charged gravastar has zero entropy density for the interior region. Using the concept of Mazur and Mottola, we evaluate the entropy of thin-shell gravastar through the expression [17]
The entropy density for local temperature can be expressed as
where \(\vartheta \) is a dimensionless parameter. Here, we take Planck units \((K_B = 1 = \hbar )\) so that the shell’s entropy becomes [17]
It is shown that entropy of the shell’s region is also proportional to the shell’s thickness. We use this equation to examine the contribution of charge and mass of BH on the entropy of shell graphically. Figure 8 shows the linear relation between entropy and thickness for different values of the physical parameter. It is found that the entropy of shell region increases by increasing Q and decreases for large values of m. The interior region of gravastars obeys the EoS \(p=-\sigma \) which represents negative energy zone with non-attractive force. The energy distribution in the shell’s region can be determined as [17]
The energy contents depend on the thickness of the shell, mass and charge of the geometry. We see that energy within the shell decreases for large values of charge and increases for large values of mass as shown in Fig. 9.
It is concluded that these features are proportional to the thickness of the shell and are greatly affected by the charge and mass of the BH which is consistent with the literature [17,18,19].
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
Funded by SCOAP3
About this article
Cite this article
Sharif, M., Javed, F. Stability of charged thin-shell gravastars with quintessence. Eur. Phys. J. C 81, 47 (2021). https://doi.org/10.1140/epjc/s10052-020-08802-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-020-08802-1