1 Introduction

Compact objects such as neutron stars and the more specialised strange quark stars are ideal candidates for applying Einstein’s theory of general relativity and for studying matter under extreme conditions. Such compact systems also draw attention to the characteristics and interactions of quarks and how this manifests itself within the physical properties of these stars. The pioneering works of Witten [1] and more recently that of Weber [2] include in-depth studies into the stability and properties of quark matter and the possibility for the existence of strange-matter stars. From the point of view of the microphysics of compact matter, the basic features of the theory of quantum chromodynamics (QCD) have been used to assist in formulating equations of state (EoS) [3]. In the context of massive compact objects such as quark-stars, the large masses, high energy densities and pressures involved require relativistic treatments using Einstein’s theory of general relativity (GR) or the more recent higher-order gravity theories such as Einstein–Gauss–Bonnet gravity [4].

Equations of state remain a key aspect in the study of compact objects. In work involving GR, equations of state have been used in setting gravitational potentials and also ensuring that physical viability is maintained. In particular, the linear equation of state, \(p = \alpha (\rho - \rho _s)\) has been popular and successful in numerous studies [5, 6]. The colour-flavour-locked equation of state has also recently been actively utilised [7], allowing for a more in-depth description of the microphysics of highly compact material which has surpassed the nuclear saturation density. If strange stars have a non-homogeneous, shell-type internal structure, as proposed for neutron stars, then different regions within the quark matter might invite the use of say region-specific equations of state as opposed to using a single EoS for the entire description of the star. This has already been considered in so-called hybrid stars [8] in which the high pressures and energy densities of the quark core might be underestimated by the simplistic linear equation of state. Thus for neutron stars of the order of \(2M_\odot \) or greater, a quadratic equation of state offers the possibility for augmenting the pressures and densities within the core of these more massive stars. The quadratic EoS has been investigated and found to offer exact solutions to the Einstein–Maxwell field equations which are physically acceptable [9,10,11]. Physical characteristics within a star could include additional processes such as the production of hyperons and generation of condensates, and an environment for the production of hyperons and generation of condensates would be favoured by higher core densities and pressures. A recent method in which a quadratic EoS is employed for taking into account the distinguishing features of the core of massive relativistic stars is the core-envelope method [11, 12]. Although we do not employ this method in our study, it nevertheless promotes the use of the quadratic equation of state for superdense, massive objects.

In considering highly compact matter from the viewpoint of GR, it is necessary to employ gravitational potentials suited to superdense matter. The Vaidya–Tikekar potential which is known to generate superdense stellar models, is favourable in this case [13]. Within the ansatz is the spheroidal parameter K which was originally set at \(K = -2\) by Vaidya and Tikekar. This however can be adjusted to improve the computed physical characteristics for the star, should certain quantities such as pressure anisotropy and sound speed show unreasonable behaviour or if the system shows marked instability. Other metric potentials such as that of Finch and Skea [14] have also been employed in compact systems governed by a quadratic equation of state [15] although the extension back to the linear regime might not be possible. Such a restriction does not arise in our study.

Pressure anisotropy is also a key feature of our model. Since the pioneering work of Bowers and Liang [16], the benefits of considering systems which incorporate anisotropy have been well-noted [17, 18]. In this paper, the method used and solutions obtained are similar to those of Maharaj and Takisa [20] with the emphasis being on application to stars of known masses and well-predicted radii. This is achieved via the Vaidya–Tikekar potential. Realistic estimates of energy density, anisotropic pressures and stability parameters are sought through variation of the equation of state parameters in the quadratic EoS of the form, \(p = \alpha \rho ^2 + \beta \rho - \gamma \).

2 The field equations

We assume the spacetime manifold to be static and spherically symmetric. This assumption is consistent with the development of models used to study the physical behaviour of relativistic astrophysical objects such as neutron stars and other similarly compact objects. The interior geometry of a spherically symmetric static star is described by the line element

$$\begin{aligned} ds^{2} = -e^{2\nu (r)} dt^{2} + e^{2\lambda (r)} dr^{2} + r^{2}(d\theta ^{2} + \sin ^{2}{\theta } d\phi ^{2}), \end{aligned}$$
(1)

in Schwarzschild coordinates \((x^{a}) = (t,r,\theta ,\phi ).\) We take the energy momentum tensor for an anisotropic neutral imperfect fluid sphere to be of the form

$$\begin{aligned} T_{ij}=\text{ diag }\left( -\rho , p_r, p_t, p_t\right) , \end{aligned}$$
(2)

where \(\rho \) is the energy density, \(p_r\) is the radial pressure and \(p_t\) is the tangential pressure. These quantities are measured relative to the comoving fluid 4-velocity \(u^i = e^{-\nu }\delta ^i_0.\) For the line element (1) and matter distribution (2) the Einstein field equations can be expressed as

$$\begin{aligned} \rho= & {} \frac{1}{r^{2}} \left[ r(1-e^{-2\lambda }) \right] ', \end{aligned}$$
(3)
$$\begin{aligned} p_r= & {} - \frac{1}{r^{2}} \left( 1-e^{-2\lambda } \right) + \frac{2\nu '}{r}e^{-2\lambda }, \end{aligned}$$
(4)
$$\begin{aligned} p_t= & {} e^{-2\lambda }\left( \nu '' + \nu '^{2} + \frac{\nu '}{r}- \nu '\lambda ' - \frac{\lambda '}{r} \right) , \end{aligned}$$
(5)

where primes denote differentiation with respect to r and our choice of units are such that \(8\pi G/c^4 = 1\). The system of equations (3)–(5) governs the behaviour of the gravitational field for an anisotropic imperfect fluid. The mass contained within a radius r of the sphere is then given by

$$\begin{aligned} m(r)= \frac{1}{2} \int _0^r\omega ^2 \rho (\omega )d\omega . \end{aligned}$$
(6)
Table 1 Model parameters (\(K = -5\))
Full size table

The field equations can be cast in a different but equivalent form by introducing the transformation

$$\begin{aligned} x = Cr^2,\quad Z(x) = e^{-2\lambda (r)}, \quad y^{2}(x) = e^{2\nu (r)} \end{aligned}$$
(7)

where C is a positive real constant. This transformation was first suggested by Durgapal and Bannerji [21]. Under this transformation, the system (3)–(5) is described by

$$\begin{aligned} \frac{1-Z}{x} - 2\dot{Z}= & {} \frac{\rho }{C}, \end{aligned}$$
(8)
$$\begin{aligned} 4Z\frac{\dot{y}}{y} + \frac{Z-1}{x}= & {} \frac{p_r}{C}, \end{aligned}$$
(9)
$$\begin{aligned} 4x Z \frac{\ddot{y}}{y} +(4 Z+ 2 x \dot{Z}) \frac{\dot{y}}{y} + \dot{Z}= & {} \frac{p_t}{C}, \end{aligned}$$
(10)

where dots denote differentiation with respect to the variable x. The mass function (6) as computed under the above transformation is given by

$$\begin{aligned} m(x)=\frac{1}{4 C^{3/2}} \int _0^x\sqrt{w}\rho (w)dw. \end{aligned}$$
(11)

For a physically realistic relativistic star we expect that the matter distribution should satisfy a barotropic equation of state \(p_r=p_r(\rho )\) and in this study we proceed with a quadratic equation of state of the form

$$\begin{aligned} p_r = \alpha \rho ^2 +\beta \rho -\gamma , \end{aligned}$$
(12)

where \(\alpha , \beta \) and \(\gamma \) are real constants. Then it is possible to write the system (8)–(10) in the simpler form

$$\begin{aligned} \frac{\rho }{C}= & {} \frac{1-Z}{x}-2 \dot{Z}, \end{aligned}$$
(13)
$$\begin{aligned} p_r= & {} \alpha \rho ^2 +\beta \rho -\gamma , \end{aligned}$$
(14)
$$\begin{aligned} p_t= & {} p_r +\varDelta , \end{aligned}$$
(15)
$$\begin{aligned} \frac{\varDelta }{C}= & {} 4 x Z \frac{\ddot{y}}{y} + \dot{Z} \left( 1+ 2x \frac{\dot{y}}{y}\right) +\frac{1-Z}{x}, \end{aligned}$$
(16)
$$\begin{aligned} \frac{\dot{y}}{y}= & {} \frac{\alpha C}{4Z}\left[ \frac{1-Z}{x} - 2 \dot{Z}\right] ^2 + \frac{\beta }{4Z}\left[ \frac{1-Z}{x} - 2 \dot{Z}\right] \nonumber \\&+ \frac{1-Z}{4xZ}-\frac{\gamma }{4CZ}, \end{aligned}$$
(17)

where the quantity \(\varDelta = p_t - p_r\) is a measure of the pressure anisotropy. A similar approach has been followed based on a linear equation of state [22]. The above system of equations governs the behaviour of the gravitational field for an imperfect fluid source.

3 Exact models

In the system (13)–(17), there are six independent variables \((\rho , p_r, p_t, \varDelta ,y,Z)\) and only five independent equations. This suggests that it is possible to specify one of the quantities involved in the integration process. Equation (17) is the master equation in the integration process. In this treatment we specify the gravitational potential Z so that it is possible to integrate (17). The explicit solution of the field equations (13)–(17) then follows. We choose

$$\begin{aligned} Z= \frac{(1 - x)}{(1 - K x)}, \end{aligned}$$
(18)

where K is a real constant. The gravitational potential Z was originally used by Vaidya and Tikekar [13] and more recently by Bhar [27] to study superdense stars, and the form of (18) has been found to be physically reasonable. Substituting (18) into (17) we obtain

$$\begin{aligned} \frac{\dot{y}}{y}= & {} \frac{\alpha C(1-K)^{2}}{4} \frac{(3 - K x)^{2}}{(1 - x) (1 - K x)^{3}} + \frac{\beta (1 -K) (3- K x)}{4 (1 - x) (1 - K x)} \nonumber \\&+\frac{(1-K)}{4(1-x)}-\frac{\gamma (1-Kx)}{4C(1-x)} \end{aligned}$$
(19)
Fig. 1
figure 1

Density profiles

Full size image

On integrating (19) we then obtain

$$\begin{aligned} y= & {} d (1 - x)^{\frac{\alpha C (3 - K)^2}{4 (K - 1)} - \frac{\beta (3 - K)}{4} + \frac{(K - 1) (C - \gamma )}{4 c}} (1 - K x)^{\frac{\alpha C (3 - K)^2}{4 (1 - K)}+ \frac{\beta }{2} } \nonumber \\&\times \,\exp \left[ \frac{\alpha C (K - 1)}{2 (1 - K x)^2} - \frac{\alpha C (2 - K)}{(1 - K x)} - \frac{\gamma K x}{4 C} \right] , \end{aligned}$$
(20)

where d is the constant of integration. Hence an exact model for the system (13)–(17) is as follows:

$$\begin{aligned} e^{2\lambda }= & {} \frac{(1 - Kx)}{(1 - x)} \end{aligned}$$
(21)
$$\begin{aligned} e^{2\nu }= & {} (1 - x)^{\frac{\alpha C (3 - K)^2}{2 (K - 1)} - \frac{\beta (3 - K)}{2} + \frac{(K - 1) (C - \gamma )}{2C}} (1 - K x)^{\frac{\alpha C (3 - K)^2}{2 (1 - K)}+ \beta } \nonumber \\&\times \, d^2 \exp \left[ \frac{\alpha C (K - 1)}{(1 - K x)^2} - \frac{2\alpha C (2 - K)}{(1 - K x)} - \frac{\gamma K x}{2 C} \right] \end{aligned}$$
(22)
$$\begin{aligned} \rho= & {} \frac{C(1-K)(3-Kx)}{(1-Kx)^2} \end{aligned}$$
(23)
$$\begin{aligned} p_r= & {} \alpha \rho ^{2} + \beta \rho - \gamma , \end{aligned}$$
(24)
$$\begin{aligned} p_t= & {} C \bigg [ \frac{4x(1 - x)}{(1 - K x)} \frac{\ddot{y}}{y} + \left( \frac{4 - 2 (3 + K) x + 4 K x^2}{(1 - K x)^2}\right) \frac{\dot{y}}{y} \nonumber \\&+\frac{K-1}{(1-Kx)^2}\bigg ]. \end{aligned}$$
(25)
Fig. 2
figure 2

Pressure profiles (\(K = -5\))

Full size image

The solution (21) – (25) may now be applied to modelling an anisotropic, relativistic star according to a quadratic equation of state. Applying the solution to (11), the mass function takes the form

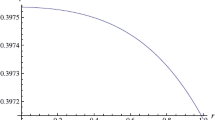
$$\begin{aligned} m(x)=\frac{(1 - K) x^{3/2}}{2\sqrt{C} (1- K x)}. \end{aligned}$$
(26)

The surface redshift is given by

$$\begin{aligned} z_s = e^\lambda - 1. \end{aligned}$$
(27)

which can be expressed in terms of the Vaidya–Tikekar potential to yield

$$\begin{aligned} z_s = \sqrt{\frac{1 - Kx}{1 - x}} - 1. \end{aligned}$$
(28)

The proper radius is given by

$$\begin{aligned} R_p = \int {e^{\lambda (r)}} dr. \end{aligned}$$
(29)
Fig. 3
figure 3

Anisotropy profiles

Full size image

4 Physical constraints

In assessing the physical viability of solutions to Einstein’s field equations, the following conditions are tested, and implemented in the case of boundary conditions, for compact, anisotropic fluid spheres [17, 18]:

  1. (i)

    non-negative values for the energy density \(\rho \) and the radial pressure \(p_r\) inside the star;

  2. (ii)

    monotonically decreasing profiles of the energy density \(\rho \), the radial pressure \(p_r\) and the tangential pressure \(p_t\) from centre to surface;

  3. (iii)

    vanishing radial pressure \(p_r\) at the surface boundary;

  4. (iv)

    subluminal sound speeds within the static configuration,

    i.e., \(\displaystyle 0 \le V_{rs}^2=\frac{dp_r}{d\rho }\le 1\) and \(\displaystyle 0 \le V_{ts}^2= \frac{dp_t}{d\rho }\le 1\);

  5. (v)

    stability condition,

    i.e., \(-1 \le V_{ts}^2 -V_{rs}^2 \le 0\);

  6. (vi)

    constraints for the energy-momentum tensor: \(\rho -p_r-2p_t\ge 0\) and \(\rho +p_r+2p_t\ge 0\);

  7. (vii)

    smooth matching of the interior metric with the exterior Schwarzschild metric at the boundary of the star \(r=R\),

    $$\begin{aligned} ds^2= & {} - \left( 1 - \frac{2M}{r} \right) dt^2 +\left( 1 - \frac{2M}{r} \right) ^{-1} dr^2 \\&+ r^2 (d\theta ^2 +\sin ^2\theta d\phi ^2), \end{aligned}$$

    where M is the total mass of the sphere.

Fig. 4
figure 4

Speed of sound squared

Full size image

5 Physical application

Three well-studied systems, Cen X-3, Vela X-1 and PSR J1614-2230 [19], were selected with evenly spaced masses above \(1.4M_\odot \) as shown in Table 1. Stars of lower mass were avoided as the lower central densities and pressures expected for such systems would be less suited to our gravitational model.

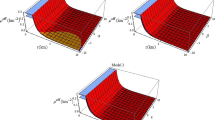
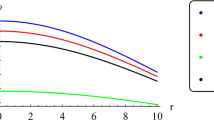
The value of \(\beta \) was set at 1/3 which is consistent with the MIT Bag model equation of state (EoS). For the model in which \(\alpha = 0\), corresponding to a linear EoS, the value of \(\gamma \) used corresponds to a Bag constant of \(\mathscr {B} = 93.5~\mathrm{MeV}/\mathrm{fm}^3\). The quadratic term in the EoS was then applied and the coefficient \(\alpha \) increased for more massive stars. It is noteworthy that the surface density, as determined by \(\gamma \), varied little so that the effect of \(\alpha \) is highlighted. The effect of the quadratic term in the EoS is shown in Figs. 1 and 2. The spheroidal parameter, K, was set at \(K = -5\) which provides for a more marked spatial variation within the metric in comparison with the original value used by Vaidya and Tikekar of \(K = -2\). A value of \(-2\) was initially investigated in our study and significantly lower densities and pressures were obtained. In addition, the anisotropy profiles for \(K=-2\) displayed some unphysical characteristics, especially for lower mass stars. The anisotropy profiles for our systems utilising \(K = -5\) are more typical in both magnitude and curve progression as shown in Fig. 3.

Fig. 5
figure 5

Stability condition

Full size image
Fig. 6
figure 6

Energy conditions

Full size image

6 Discussion

We now provide further discussion of the trends and physical viability of our models. In Fig. 1 we observe that the density profiles are smooth, monotonically decreasing functions of the radial coordinate. As the quadratic parameter \(\alpha \) increases, the magnitude of the density increases at each interior point of the compact object. Figure 2 (left panel) displays the radial pressure as a function of the radial coordinate. As expected, the radial pressure decreases monotonically from some finite value at the centre and vanishes at the boundary of the star. It is interesting to note that an increase in \(\alpha \) supports configurations with larger radii. This confirms the trend in the density profiles - larger values of \(\alpha \) lead to higher densities. We observe that the tangential pressure (Fig. 2, right panel) is well-behaved. Higher contributions from the quadratic term lead to higher tangential pressures. The anisotropy parameter is plotted in Fig. 3. For each interior point of the stellar configuration, \(\varDelta > 0\). This means that tangential pressure dominates the radial pressure everywhere inside the star. A positive anisotropy parameter leads to a repulsive contribution from the anisotropic force which may lead to more massive and stable configurations. Figure 4 (left and right panels) indicate that our model obeys the causality requirements. An interesting feature is the minima which appear in the tangential sound speed. This could model an additional anisotropy which distinguishes material closer to the surface from that of the core. The cracking method due to Herrera ascertains that if the tangential speed of pressure wave \(v_t\) exceeds the radial speed \(v_r\), then the model is potentially stable. This requirement can be articulated mathematically as \(v_t^2 - v_r^2 < 0\). We observe from Fig. 5 that the interior of our stellar model is stable. We further observe that this stability is enhanced with an increase in the quadratic contributions from the EoS. Our model obeys the energy conditions as revealed in Fig. 6. In addition, we have plotted the stability index, \(\varGamma \) in Fig. 7. We note that \(\varGamma > 4/3\) everywhere inside the stellar fluid. We have compared the quadratic EoS to the colour-flavour locked (CFL) EoS and the linear EoS in Fig. 8. Similar plots and comparisons have been found in the literature for linearly approximated EoS’s [23] and the more recently pursued CFL EoS [24,25,26]. It is interesting to note that the quadratic EoS mimics the CFL EoS more closely than the linear EoS. This is a new and interesting observation. Thirukannesh et al. [7] recently showed that the linear EoS closely resembles the CFL EoS. Our study shows that a better approximation to the CFL EoS is the quadratic EoS. The surface redshift is plotted in Fig. 9. We observe that the redshift increases with an increase in radius and that our results compare well with other studies [27,28,29]. Furthermore, we observe higher surface redshifts for larger values of \(\alpha \). This ties in with our earlier observation that larger values of \(\alpha \) lead to higher densities.

Fig. 7
figure 7

Adiabatic index profiles

Full size image
Fig. 8
figure 8

Comparison of equations of state

Full size image
Fig. 9
figure 9

Surface redshift with respect to proper radius

Full size image

7 Conclusion

We have shown that the quadratic equation of state is well-suited to the description of highly dense and massive neutron stars, strange-matter stars and possibly the more exotic hybrid stars for which higher core densities and pressures are sought. Our results have shown the effectiveness of the quadratic term in achieving the higher densities and pressures while maintaining stability of the core. Pressure anisotropy is a key feature of our models and the anisotropy parameter displayed radial profiles which were favourable and comparable to other studies. The Vaidya–Tikekar potential used, with the spheroidal parameter \((K = -5)\) used, resulted in the possibility of an additional inhomogeneity as suggested by the minima in the tangential sound speed profiles. According to the sound speed stability criterion, our models appear to be stable except possibly near the surface which could result in a crust which exhibits cracking. The phenomenon of cracking and its relationship to inhomogeneity and anisotropy has been studied by Herrera et al. [18] and the necessity for pressure anisotropy appears to be of central importance in the stability of compact, relativistic objects. The possible instability near the surface as shown in our results may however be reduced by increasing the effect of the quadratic term in the EoS used in this study. Hence the benefit of the quadratic term is highlighted. Comparison of the quadratic equation of state with the linear and the CFL equations of state show that the quadratic term is to some extent a perturbation, featuring more prominently in the core, and that the values of \(\alpha \) used serve as adjustments where linearity is likely to fail. The quadratic term also shows enhancements of the surface redshift. Lastly, the adiabatic index shows that the configurations are stable and that increasing \(\alpha \) results in a reduction in the rate of decline in stability, albeit the index remaining above Chandrasekhar’s limit \((\varGamma \ge 4/3)\). The apparent reverse trend in stability as compared to the potential instability analysis as given by the sound speed anisotropy results in Fig. 5, are no doubt a result of the different masses and radii of the candidate stars used in our investigation. In light of this, it is proposed that for a future investigation of the quadratic equation of state with the Vaidya–Tikekar potential, a single candidate star be chosen and studied with respect to variation in the spheroidal parameter.