1 Introduction

Black holes are intriguing astrophysical objects and perhaps the most fascinating objects in the Universe and it is hard to find any other object or topic that attracts more attention. However, it is still not clear whether black holes can be observed. Observation of the shadow of black hole candidate Sagittarius \(\hbox {A}^*\) or Sgr \(\hbox {A}^*\) is one of the most important goals of the Very Large Baseline Interferometry (VLBI) technique. It should able to image the black hole with resolution at the level of the event horizon. At galactic center the black hole candidate Sgr \(\hbox {A}^*\), due to the gravitational lensing effect, casts a shadow; the shape and size of this shadow can be calculated. There is a widespread belief that evidence for the existence of black holes will come from the direct observation of its shadow. The shape of a shadow could be used to study extreme gravity near the event horizon and also to know whether the general relativity is consistent with the observations. Observation of a black hole shadow may allow us to determine the mass and spin of a rotating black hole [1,2,3,4,5,6]. As black holes are basically non-emitting objects, it is of interest the study null geodesics around them where photons coming from other sources move to lead to a shadow. To a distant observer, the event horizons cast shadows due to the bending of light by a black hole [7]. A first step towards the study of a black hole shadow was done by Bardeen [8], who calculated the shape of a dark area of a Kerr black hole, i.e., its shadow over a bright background. Although the shadow of Schwarzschild black hole is a perfect circle [9, 10], the Kerr black hole does not have a circular shadow image; it has an elongated shape in the direction of rotation [11]. The pictures of individual spherical light-like geodesics in the Kerr spacetime can be found in [12], and one can find a discussion and the picture of the photon region in the background of Kerr spacetime in Ref. [13].

Thus, the shadow deviation from the circle can determine the spin parameter of black holes. The study of black holes has been extended for other black holes, such as Kerr black holes [8], Kerr-Newman black holes [14], regular black holes [15,16,17] black holes, multi-black holes [18], black holes in extended Chern–Simons modified gravity [19] and for the Randall–Sundrum braneworld case [20]. The shadows of black holes with nontrivial NUT charge were obtained in [21], while the Kerr–Taub–NUT black holes were discussed in [22]. The apparent shape of the Kerr–Sen black holes is studied in [23], and rotating braneworld black holes were investigated in [20, 24]. Further, the effect of the spin parameter on the shape of the shadow was extended to the Kaluza–Klein rotating dilaton black hole [25], the rotating Horava–Lifshitz black hole [26], the rotating non-Kerr black hole [27] and the Einstein–Maxwell–dilaton-axion black hole [28]. There are different approaches to calculating the shadow of the black holes, e.g., a coordinate-independent characterization [29] and by general relativistic ray-tracing [30].

Recent years witnessed black hole solutions in more than four spacetime dimensions, especially in five dimensions as the subject of intensive research motivated by ideas in the braneworld, string theory and gauge/gravity duality. Several interesting and surprising results have been found in [31]. The models with large, extra dimensions have been proposed to deal with several issues arising in modern particle phenomenology [31,32,33,34]. The rotating black holes have many applications and display interesting structures, but they are also very difficult to find in higher dimensions and the bestiary for solutions is much wider and less understood [35, 36]. The uniqueness theorems do not hold in higher dimensions due to the fact that there are more degrees of freedom. The black-ring solution in five dimensions shows that higher-dimensional spacetime can admit nontrivial topologies [37]. The Myers–Perry black hole solution [38] is a higher-dimensional generalization of the Kerr black hole solution. However, the Kerr–Newman black hole solution in higher dimensions has not yet been discovered. Nevertheless, there is a related solution of the Einstein–Maxwell–Chern–Simons (EMCS) theory in five-dimensional minimal gauged supergravity [39, 40]. Remarkably, the exact five-dimensional solutions for rotating charged black holes are known in the Einstein–Maxwell theory with a Chern–Simons term. The extremal limits of the five-dimensional rotating charged black hole solutions are of special interest, since they encompass a two parameter family of stationary supersymmetric black holes. The shadow of the five-dimensional rotating black hole [41] suggests that the shadow is slightly smaller and less deformed than for its four-dimensional Kerr black hole counterpart. Recently, the shadow of a higher-dimensional Schwarschild–Tangherlini black hole was discussed in [42] and the results show that the size of the shadows decreases in higher dimensions.

The aim of this paper is to investigate the shadow of a five-dimensional EMCS minimal gauged supergravity black hole (henceforth five-dimensional EMCS black hole) and compare the results with the Kerr black hole/five-dimensional Myers–Perry black hole. We have discussed in detail the structure of the horizons and the shadows of EMCS black holes in five dimensions, focusing on solutions with equal magnitude angular momenta, to enhance the symmetry of the solutions, making the analytical analysis much more tractable, while at the same time revealing already numerous intriguing features of the black hole shadows.

The paper is organized as follows. In Sect. 2, we review the five-dimensional Myers–Perry black hole solution and also visualize the ergosphere for various values of the charge q. In Sect. 3, we present the particle motion around the five-dimensional EMCS black hole to discuss the black hole shadow. Two observables are introduced to discuss the apparent shape of the black hole shadow in Sect. 4. The naked singularity shadow of the five-dimensional EMCS spacetime is the subject of Sect. 5. We discuss the energy emission rate of the five-dimensional EMCS black hole in Sect. 6 and finally we conclude with the main results in Sect. 7.

We have used units that fix the speed of light and the gravitational constant via \(8\pi G=c=1\).

2 Rotating five-dimensional EMCS black holes

It is well known that the stationary black holes in five-dimensional EMCS theory possess surprising properties when considering the Chern–Simons coefficient as a parameter. We briefly review the five-dimensional asymptotically flat EMCS black hole solutions. The Lagrangian for the bosonic sector of the minimal five-dimensional supergravity reads [43, 44]:

$$\begin{aligned} {\mathcal L}= \frac{1}{16\pi } \left[ \sqrt{-g}(R -F^2) - \frac{2}{3\sqrt{3}}\epsilon ^{\mu \nu \rho \sigma \tau }A_\mu F_{\nu \rho }F_{\sigma \tau }\right] ,\nonumber \\ \end{aligned}$$
(1)

where R is the curvature scalar, \( F_{\mu \nu } = \partial _\mu A_\nu -\partial _\nu A_\mu \) with \(A_{\mu }\) is the gauge potential, and \(\epsilon ^{\mu \nu \lambda \rho \sigma }\) is the five-dimensional Levi-Civita tensor. The Lagrangian (1) has an additional Chern–Simons term different from the usual Einstein–Maxwell term. The corresponding equations of motion reads [44, 45]

$$\begin{aligned}&R_{\mu \nu }-\frac{1}{2}g_{\mu \nu }R = 2\left( F_{\mu \alpha }F_{\nu \alpha } -\frac{1}{4}g_{\mu \nu }F_{\rho \sigma }F^{\rho \sigma }\right) , \nonumber \\&\nabla _{\mu } \left( F^{\mu \nu }+\frac{1}{\sqrt{3} \sqrt{-g}}\epsilon ^{\mu \nu \lambda \rho \sigma } A_{\lambda } F_{\rho \sigma }\right) = 0. \end{aligned}$$
(2)

A five-dimensional rotating EMCS black hole solution [44], in Boyer–Lindquist coordinates (\(t, r, \theta , \phi , \psi \)), can be expressed by the metric

$$\begin{aligned} {\text {d}}s^2= & {} - \frac{\rho ^2 {\text {d}}t^2 + 2q\nu {\text {d}}t}{\rho ^2} + \frac{2q \nu \omega }{\rho ^2} + \frac{\mu \rho ^2 - q^2}{\rho ^4} \left( {\text {d}}t - \omega \right) ^2 \nonumber \\&+\, \frac{\rho ^2 {\text {d}}x^2}{4\Delta } + \rho ^2 {\text {d}}\theta ^2 + \left( x+a^2 \right) \sin ^2 \theta {\text {d}}\phi ^2 \nonumber \\&+ \,\left( x+b^2 \right) \cos ^2 \theta {\text {d}}\psi ^2, \end{aligned}$$
(3)

where the gauge potential for the metric (3) can be expressed as

$$\begin{aligned} A_\mu {\text {d}}x^\mu = \frac{\sqrt{3} \, q}{\rho ^2} \left( {\text {d}}t - \omega \right) \end{aligned}$$
(4)

and

$$\begin{aligned} \Delta= & {} \left( x+a^2 \right) \left( x+b^2 \right) + q^2 +2 abq - \mu x, \nonumber \\ \rho ^2= & {} x + a^2 \cos ^2 \theta + b^2 \sin ^2 \theta , \nonumber \\ \nu= & {} b \sin ^2 \theta \, {\text {d}}\phi + a \cos ^2 \theta {\text {d}}\psi , \nonumber \\ \omega= & {} a \sin ^2 \theta {\text {d}}\phi + b \cos ^2 \theta {\text {d}}\psi , \end{aligned}$$
(5)

where \(\mu \) is related to the black hole mass, q is the charge and a, b are the two different angular momenta of the black hole. Furthermore, the non-zero components of the metric (3) can be expressed as

$$\begin{aligned} g_{tt}= & {} \frac{ \rho ^2(\mu -\rho ^2) -q^2 }{\rho ^4},\nonumber \\ g_{t\phi }= & {} -\frac{a (\mu \rho ^2-q^2) + b q\rho ^2\sin ^2\theta }{\rho ^4},\nonumber \\ g_{t\psi }= & {} -\frac{b (\mu \rho ^2-q^2) + a q\rho ^2 \cos ^2\theta }{\rho ^4 },\nonumber \\ g_{\phi \psi }= & {} \frac{[ ab(\mu \rho ^2 -q^2) + (a^2+b^2) q \rho ^2] \sin ^2\theta \cos ^2\theta }{\rho ^4},\nonumber \\ g_{xx}= & {} \frac{\rho ^2}{\Delta },\qquad g_{\theta \theta }={\rho ^2}, \nonumber \\ g_{\phi \phi }= & {} {(x+a^2)\sin ^2\theta } + \frac{ a[a(\mu \rho ^2 -q^2) + 2 bq \rho ^2]\sin ^4\theta }{\rho ^4 },\nonumber \\ g_{\psi \psi }= & {} {(x+b^2)\cos ^2\theta } + \frac{ b[b(\mu \rho ^2 -q^2) + 2 aq \rho ^2]\cos ^4\theta }{\rho ^4 }.\nonumber \\ \end{aligned}$$
(6)

The radial coordinate has been changed to a new radial coordinate x via \(x=r^2\). One can check that, for \(q=0\), the five-dimensional EMCS black hole reduces to the five-dimensional Myers–Perry black hole, which is analyzed in [38, 41], and also in addition if \(a=0\), it reduces to the five-dimensional Schwarschild–Tangherlini black hole [46]. It may be noted that the metric (3) is independent of the coordinates (\(t, \phi , \psi \)), and hence it admits three Killing vectors, given by

$$\begin{aligned} \ell= & {} \frac{\partial }{\partial t} + \Omega _a\, \frac{\partial }{\partial \phi } + \Omega _{\text {b}} \, \frac{\partial }{\partial \psi }, \end{aligned}$$
(7)

and these Killing vectors become null at the event horizon. The angular velocities for the metric (3) can be defined as

$$\begin{aligned} \Omega _a= & {} \frac{a(x^{H}_{+} + b^2)+ b q}{(x^{H}_{+} + a^2)(x^{H}_{+} +b^2) + ab q},\nonumber \\ \Omega _{\text {b}}= & {} \frac{b(x^{H}_{+} + a^2)+ a q}{(x^{H}_{+} +a^2)(x^{H}_{+} +b^2) + ab q}, \end{aligned}$$
(8)

where \(x^{H}_{+}\) denotes the event horizon of the five-dimensional EMCS black hole. The surface gravity of the EMCS black hole (3) takes the following form [39]:

$$\begin{aligned} \kappa= & {} \frac{(x^{H}_{+})^2-(ab + q)^2}{\sqrt{x^{H}_{+}} [(x^{H}_{+} +a^2)(x^{H}_{+} +b^2) + abq]}. \end{aligned}$$
(9)

The five-dimensional EMCS black hole obeys the first law of thermodynamics and with the help of the surface gravity (9), the Hawking temperature of the black hole can easily be calculated via \(T=\kappa /(2\pi )\). The entropy of the black hole is given [39] by

$$\begin{aligned} S= & {} \frac{\pi ^2 [(x^{H}_{+}+a^2)(x^{H}_{+} + b^2) +a b q]}{2\sqrt{x^{H}_{+}}}, \end{aligned}$$
(10)

when \(a=b=0=q\), it reduces to

$$\begin{aligned} S= & {} \frac{\pi ^2 {(x^{H}_{+}})^{3/2}}{2}. \end{aligned}$$
(11)

The Komar integral reads

$$\begin{aligned} J = \frac{1}{16\pi }\int _{S^3} {*{\text {d}}K}, \end{aligned}$$
(12)

where \(K=\partial /\partial \phi \) or \(K=\partial /\partial \psi \), yielding

$$\begin{aligned} J_a = \frac{\pi (\mu a + qb)}{4}, \quad J_{\text {b}} = \frac{\pi (\mu b + qa)}{4}. \end{aligned}$$
(13)

The electric charge can be calculated by the Gaussian integral

$$\begin{aligned} Q=\frac{1}{16\pi }\int _{S^3}( {*F} -F\wedge A/\sqrt{3}), \end{aligned}$$
(14)

which gives

$$\begin{aligned} Q= & {} \frac{\sqrt{3}\, \pi q}{4}. \end{aligned}$$
(15)

As is well known the five-dimensional EMCS black hole follows the first law of thermodynamics so the conserved mass or the energy can be calculated by integrating

$$\begin{aligned} {\text {d}}E=T{\text {d}}S + \Omega _a {\text {d}}J_a + \Omega _{\text {b}} {\text {d}}J_{\text {b}} + \Phi {\text {d}}Q, \end{aligned}$$
(16)

where \(\Phi \) is the electrostatic potential. Integrating Eq. (16), we obtain

$$\begin{aligned} E= & {} \frac{3\pi \mu }{8}, \end{aligned}$$
(17)

which represents the conserved energy of the five-dimensional EMCS black hole. Interestingly, the determinant is the same as the uncharged case \(\sqrt{- \det g} = \rho ^2 \sin \theta \cos \theta /2\).

2.1 Horizons and ergosphere

Our aim is to discuss the effect of the charge q on the horizons and also on the ergosphere. It can be seen that the metric (3) is singular at \(\rho ^2=0\) and \(\Delta =0\). Note that \(\rho ^2=0\) is a physical singularity and \(\Delta = 0\) gives a coordinate singularity which defines the horizons of the metric (3). It turns out that \(\Delta =0\) admits two roots [44],

$$\begin{aligned} x^{H}_{\pm } = \frac{1}{2} \left( \mu - a^2 - b^2 \pm \sqrt{\left( \mu - a^2 - b^2 \right) ^2 - 4\left( ab+q \right) ^2} \right) ,\nonumber \\ \end{aligned}$$
(18)

which correspond to the five-dimensional EMCS black hole with two regular horizons, the event horizon (\(x^H_{+}\)) and the Cauchy horizon (\(x^H_{-}\)), when \((\mu -a^2-b^2)^2 > 4(ab+q)^2\) or \(\mu > (a + b)^2 +2q \) [44]. It represents an extremal black hole with degenerate horizons (\(x^H_+=x^H_-\)) when \( \mu = (a+b)^2 +2q\), and a naked singularity when \(\mu < (a + b)^2 +2q \). If \(q=0\), Eq. (18) takes the following form:

$$\begin{aligned} x^{H}_{\pm } = \frac{1}{2} \left( \mu - a^2 - b^2 \pm \sqrt{\left( \mu - a^2 - b^2 \right) ^2 - 4a^2b^2} \right) , \end{aligned}$$
(19)

where the two roots show the two horizons of the Myers–Perry spacetime [38, 41]. If we consider the case when both spin parameters are equal \((a=b)\), then Eq. (18) reduces to

$$\begin{aligned} x^{H}_{\pm } = \frac{1}{2} \left( \mu - 2a^2 \pm \sqrt{\left( \mu - 2a^2 \right) ^2 - 4\left( a^2+q \right) ^2} \right) . \end{aligned}$$
(20)

In this case the extremal black hole occurs at \(\mu =2(2 a^2 +q)\), a naked singularity occurs at \(\mu <2(2a^2+q)\), and a non-extremal black hole exists at \(\mu >2(2a^2+q)\). Thus, the black hole charge affects the horizon structure and when \(q=0\), Eq. (20) reduces to

$$\begin{aligned} x^{H}_{\pm } = \frac{1}{2} \left( \mu - 2a^2 \pm \sqrt{\left( \mu - 2a^2 \right) ^2 - 4a^4 } \right) , \end{aligned}$$
(21)
Fig. 1
figure 1

Plot showing the dependence of charge q with spin a, b. (Left) For \(a \ne b\), \(a=0\) (blue solid line), \(a=0.1\) (red dashed line), \(a=0.2\) (green dashed line). (Right) For \(a=b\)

Full size image
Fig. 2
figure 2

The cross section of the event horizon, static limit surface, and ergoregion for different values of q with a fixed value of rotation parameter a for the five-dimensional EMCS black hole; the case \(q=0\) refers to the Myers–Perry black hole. The blue line indicates a static limit surface and the red one represents horizons

Full size image

which shows the two non-degenerate horizons of the five-dimensional Myers–Perry black hole [38, 41] for equal rotation parameters. Next, we find the static limit surface where the time-like Killing vectors of the metric become null, i.e., \(g_{tt}=0\), which leads to

$$\begin{aligned}&(x + a^2 \cos ^2 \theta + b^2 \sin ^2 \theta )^2 \nonumber \\&\quad - \mu (x + a^2 \cos ^2 \theta + b^2 \sin ^2 \theta )+q^2=0, \end{aligned}$$
(22)

which can be trivially solved [44],

$$\begin{aligned} x^{sls}_{\pm }=\frac{1}{2} \left( \mu \pm \sqrt{\mu ^2-4 q^2}\right) -a^2 \cos ^2 \theta -b^2 \sin ^2 \theta ; \end{aligned}$$
(23)

for equal rotation parameters \(a=b\) [44], the roots can be defined as

$$\begin{aligned} x^{sls}_{\pm }=\frac{1}{2} \left( \mu \pm \sqrt{\mu ^2-4 q^2}\right) -a^2. \end{aligned}$$
(24)

We can see that in the limit \(q \rightarrow 0\),

$$\begin{aligned} x^{sls}_{+} = \mu -a^2, \quad x^{sls}_{-} = a^2. \end{aligned}$$
(25)

It can be seen that both surfaces, i.e., the static limit surface and the horizons of the black hole, are not coinciding at the poles (\(\theta =0, \pi /2\)), and hence the ergosphere is totally different from the Kerr–Newman black hole where they do coincide at the poles (cf. Fig. 2). The only possibility is when we have chosen [44]

$$\begin{aligned} \theta = \arccos \left( \pm \sqrt{\frac{\mu }{a^2 + b^2}}\,\right) , \quad \hbox {and} \quad q=-\frac{ab\mu }{a^2 + b^2}. \end{aligned}$$

Hence, for the above values of \(\theta \) and q, both surfaces of the metric (3) coincide. Figure 1 shows the contour plots of \(\Delta =0\), for the cases when \(a\ne b\) and \(a=b\). The contours depicted in Fig. 1 indicate the boundary lines between a black hole region and the naked singularity. The coinciding roots arise on the colored line and there exist two roots inside the black hole region (cf. Fig. 1). It can also be seen from Fig. 1 that if there is no real root, then the region belongs to the naked singularity. An ergoregion is a region outside the event horizon where the time-like Killing vectors behave like space-like. A particle can enter into the ergoregion and leave again, and it moves in the direction of spin of the black hole and has relevance for the energy extraction process [47]. We have plotted the ergoregion of the five-dimensional EMCS black hole in Fig. 2 for different values of a and q, and we observe that there is an increase in the area of the ergoregion when we increase the values of the parameter q and a (cf. Fig. 2).

Fig. 3
figure 3

The cross section of the event horizon, static limit surface, and ergoregion for different values of q with a fixed rotation parameter a for the extremal five-dimensional EMCS black hole when the two horizons coincide. The blue lines indicate the static limit surface and the red ones represent horizons

Full size image

In Kerr black hole case, we have the region between the event horizon and static limit surface, known as the ergoregion, which can be seen from Fig. 2. In Fig. 2, we explicitly show the effect of the parameter q on the ergoregion, it shows that the area of ergoregion grows with the rotation parameter a as well as with the charge q. Thus, for the faster rotating black holes the ergoregion is enlarged. Figure 3 suggests that the ergoregion area is maximum for an extremal five-dimensional EMCS black hole.

3 Particle motion

Different tests were proposed to discover the signatures of extra dimensions in supermassive black holes since the gravitational field may be different from the standard one in the general relativity approach. In particular, gravitational lensing features are different for alternative gravity theories with extra dimensions and general relativity. The study of the higher-dimensional black hole shadow may help us to understand how measurements of the sizes can put constraints on the parameters of a black hole in the spacetime with extra dimensions. Next, we would like to study the shadow of the EMCS black hole, which requires a complete study of particle motion around the black hole, and it can be obtained by the Hamilton–Jacobi formalism originally suggested by Carter [48]. The Hamilton–Jacobi equation [11] for the five-dimensional EMCS black hole (3) with the metric tensor \(g_{\mu \nu }\) (6) reads

$$\begin{aligned} - \frac{\partial S}{\partial \sigma } = \frac{1}{2} g^{\mu \nu }\frac{\partial S}{\partial x^\mu } \frac{\partial S}{\partial x^\nu }, \end{aligned}$$
(26)

where \(\sigma \) is the affine parameter and S is the Jacobian action with the following separable ansatz for the Jacobian action [41]:

$$\begin{aligned} S = \frac{1}{2} m_{0}^{2} \sigma - Et + S_{\text {r}}(r) + S_\theta (\theta ) + L_{\phi } \phi + L_{\psi }\psi , \end{aligned}$$
(27)

where \(m_0\) is the mass of a test particle, which is zero in the case of a photon, and the conserved quantities E, and \(L_{\phi }\), \(L_{\psi }\) correspond to the energy and angular momentum of the particle, respectively. However, \(S_{\text {r}}(r)\) and \(S_{\theta }(\theta )\) are, respectively, functions of r and \(\theta \) only. It can be seen, using Eqs. (27) and (26), that one can find the complete geodesic equations for the five-dimensional EMCS black hole [44]:

$$\begin{aligned} \rho ^2 \frac{{\text {d}}t}{{\text {d}}\sigma }= & {} E\rho ^2+\frac{1}{\Delta }\Big [\left( \mu \zeta \gamma -q^2(\zeta +b^2 \right) E \nonumber \\&+\, \left( a\gamma \mu +b\gamma q-aq^2\right) L_\phi \nonumber \\&+\,\left( \zeta b \mu +a\zeta q-bq^2\right) L_\psi \Big ], \end{aligned}$$
(28)
$$\begin{aligned} \rho ^2 \frac{{\text {d}}\phi }{{\text {d}}\sigma }= & {} \frac{L_{\phi }}{\sin ^2\theta }-\frac{1}{\Delta }\Big [\Big ((a^2-b^2)\gamma + \mu b^2+2abq\Big )L_{\phi } \nonumber \\&+\, \Big (\mu ab+(a^2+b^2)q\Big )L_{\psi }\nonumber \\&+\,\Big (a\gamma \mu +b\gamma q-aq^2\Big )E\Big ], \end{aligned}$$
(29)
$$\begin{aligned} \rho ^2 \frac{d \psi }{{\text {d}}\sigma }= & {} \frac{L_\psi }{\cos ^2\theta }-\frac{1}{\Delta }\Big [\left( -(a^2-b^2)\zeta + \mu a^2+2abq\right) L_\psi \nonumber \\&+\, \left( \zeta b\mu +a\zeta q-bq^2\right) E\nonumber \\&+\,\Big (\mu ab+(a^2+b^2)q\Big )L_\phi \Big ], \end{aligned}$$
(30)
$$\begin{aligned} \rho ^2 \frac{{\text {d}}x}{{\text {d}}\sigma }= & {} \pm \sqrt{\mathcal R}, \end{aligned}$$
(31)
$$\begin{aligned} \rho ^2 \frac{{\text {d}} \theta }{{\text {d}}\sigma }= & {} \pm \sqrt{\Theta }, \end{aligned}$$
(32)

where \(\zeta = x+a^2\) and \(\gamma = x+b^2\). In the geodesic equations (31) and (32), the terms \({\mathcal R}\) and \(\Theta \) are given by

$$\begin{aligned} {\mathcal {R}}= & {} 4 \left( E^2 \Delta x - \Delta {\mathcal {K}} + {\mathcal {E}} + \mu {\mathcal {M}} + 2q {\mathcal {Q}} - q^2 {\mathcal {P}}\right) , \end{aligned}$$
(33)
$$\begin{aligned} \Theta= & {} E^2 \left( a^2 \cos ^2 \theta + b^2 \sin ^2 \theta \right) + {\mathcal {K}} \nonumber \\&-\,\frac{L_\phi ^2}{\sin ^2\theta }- \frac{L_\psi ^2}{\cos ^2 \theta }, \end{aligned}$$
(34)

where \({\mathcal {K}}\) is the Carter constant [48] and

$$\begin{aligned} {\mathcal {E}}= & {} (a^2-b^2)(\gamma L_\phi ^2 -\zeta L_\psi ^2), \\ {\mathcal {Q}}= & {} ab \left( L_{\phi }^2 + L_{\psi }^2\right) + (a^2+b^2) L_{\phi } L_{\psi }\\&+ \,Eab \left( \frac{L_{\phi } \gamma }{a} + \frac{L_{\psi } \zeta }{b} \right) , \\ {\mathcal {M}}= & {} \zeta \gamma E^2 + 2 a \gamma E L_\phi + 2 \zeta bEL_{\psi } + (b L_{\phi } + aL_{\psi })^2, \\ {\mathcal {P}}= & {} 2a EL_{\phi } + 2b E L_{\psi } + (\zeta +b^2)E^2. \end{aligned}$$

These geodesic equations define the geometry of photon around the spacetime of the five-dimensional EMCS black hole. For a particle that is moving in the equatorial plane and to remain in the equatorial plane, it is necessary that the Carter constant \({\mathcal {K}}\) must be zero [49]. One can recover the equations of motion of the five-dimensional Myers–Perry black hole when \(q=0\) [41]. In the presence of a bright object behind a black hole or for obtaining the boundary of the black hole shadow, the study of the radial equation is required. We can rewrite the radial equations of motion [28, 41]

$$\begin{aligned} \left( \frac{{\text {d}}x}{{\text {d}}\sigma }\right) ^2 + V_{\text {eff}}= & {} 0, \end{aligned}$$
(35)

with the effective potential

$$\begin{aligned} V_{\text {eff}}= & {} -\frac{4}{\rho ^2} \Big [E^2 \Delta x - \Delta {\mathcal {K}} + {\mathcal {E}} + \mu {\mathcal {M}} + 2q{\mathcal {Q}} - q^2 {\mathcal {P}}\Big ].\nonumber \\ \end{aligned}$$
(36)

When \(q=0\), Eq. (36) reduces to

$$\begin{aligned} V_{\text {eff}}= & {} -\frac{4}{\rho ^2} \Big [E^2 \Delta x - \Delta {\mathcal {K}} + {\mathcal {E}} + \mu {\mathcal {M}} \Big ], \end{aligned}$$
(37)

which is the effective potential of the Myers–Perry black holes [50]. The apparent shape of the five-dimensional EMCS black hole can be obtained by a study of the photon orbits.

The impact parameters characterizing the photon orbits around the black hole can be defined in terms of the constants of motion, i.e., \(\xi _{1}=L_{\phi }/E\), \(\xi _{2}=L_{\psi }/E\) and \(\eta ={\mathcal K}/E^2\). Therefore, the expression for \({\mathcal R}\) takes the form

$$\begin{aligned} {\mathcal {R}}= & {} 4 E^2 \left( \Delta x - \Delta \eta +\mu {\mathcal {J}} + 2q{\mathcal {O}} - q^2 {\mathcal {S}}\right) , \end{aligned}$$
(38)

where \({\mathcal {J}} = \zeta \gamma + 2 a (\gamma \xi _{1} + \zeta \xi _{2}) + a^2(\xi _{1} + \xi _{2})^2\), \({\mathcal {O}} = a^2 (\xi _{1}^2 + \xi _{2}^2) + 2a^2 \xi _{1} \xi _{2} + a \left( \xi _{1} \gamma + \xi _{2} \zeta \right) \), and \({\mathcal {S}} = 2a (\xi _{1} + \xi _{2}) + (\zeta +a^2)\). Henceforth, we assume that the two rotation parameters \(a=b\).

The radial motions of the photons are essential for determining the shadow of the five-dimensional EMCS black hole. The spherical photon orbits, i.e., the geodesics that stay on a sphere r = constant, define the apparent shape of the black hole. The photons come from infinity and approach a turning point with zero radial velocity, which corresponds to an unstable circular orbit determined by

$$\begin{aligned} V_{\text {eff}}=0 \quad \text {and} \quad \frac{{\text {d}} V_{\text {eff}}}{d x} =0, \quad \text {or} \quad {\mathcal {R}}=0 \quad \text {and} \quad \frac{d{\mathcal {R}}}{{\text {d}}x}=0. \end{aligned}$$
(39)

By Eqs. (36) and (39), as in the Kerr case [51], one can obtain the parameters \(\eta \) and the sum of the parameters \(\xi _1\), \(\xi _2\), which read

$$\begin{aligned}&\eta = \frac{1}{a(2q+1)(-1+2 a^2+2 x)^2}\Big [2a^7 (1+2 q) \nonumber \\&\quad +\,a^5 [1+2 q (3+3 q+10 x)+10 x] + 2 a^3 \left[ q (1+q) (1+4 q)+2 (-1+(-1+q) q) x+7 (1+2 q) x^2\right] \nonumber \\&\quad - \,2 (1+q) \sqrt{a^2 \left[ q^2+a^2 (2+4 q)+2 x+4 q x\right] \left[ a^4+q^2+(-1+x) x +2 a^2 (q+x)\right] ^2} \nonumber \\&\quad + a \left[ 2 q^3 (1+q)+4 q^2 (1+q) x -(5+2 q (5+q)) x^2+6 (1+2 q) x^3\right] \Big ] \end{aligned}$$
(40)

and

$$\begin{aligned} \xi _1 +\xi _2= & {} \frac{1}{a^2(2q +1)(-1+2 a^2+2 x)}\Big [-a^5 (1+q) +a^3 \left[ 1+3 q+4 q^2-2 (1+q) x\right] + a \left[ q^3+2 q^2 x-(1+q) x^2\right] \nonumber \\&- \,\sqrt{a^2 \left[ q^2+a^2 (2+4 q)+2 x+4 q x\right] \left[ a^4+q^2+(-1+x) x+2 a^2 (q+x)\right] ^2}\Big ]. \end{aligned}$$
(41)

The impact parameters \(\xi _1\), \(\xi _2\) and \(\eta \) for the photon orbits around the five-dimensional EMCS black hole determine the contour of the shadow [41]. Now we consider the case when \(\theta =\pi /2\), \(L_{\psi }=0\), which implies \(\xi _2=0\); therefore from Eq. (41), we obtain

$$\begin{aligned}&\xi _1 = \frac{1}{a^2(2q +1)(-1+2 a^2+2 x)}\Big [-a^5 (1+q) +a^3 \left[ 1+3 q+4 q^2-2 (1+q) x\right] \nonumber \\&\quad + \,a \left[ q^3+2 q^2 x-(1+q) x^2\right] \nonumber \\&\quad - \,\sqrt{a^2 \left[ q^2+a^2 (2+4 q)+2 x+4 q x\right] \left[ a^4+q^2+(-1+x) x+2 a^2 (q+x)\right] ^2}\Big ], \end{aligned}$$
(42)

and for \(\theta =0\), \(L_{\phi }=0\), which implies \(\xi _1=0\), thus

$$\begin{aligned} \xi _2= & {} \frac{1}{a^2(2q +1)(-1+2 a^2+2 x)}\Big [-a^5 (1+q) +a^3 \left[ 1+3 q+4 q^2-2 (1+q) x\right] \nonumber \\&+ \,a \left[ q^3+2 q^2 x-(1+q) x^2\right] \nonumber \\&- \,\sqrt{a^2 \left[ q^2+a^2 (2+4 q)+2 x+4 q x\right] \left[ a^4+q^2+(-1+x) x+2 a^2 (q+x)\right] ^2}\Big ].\qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \end{aligned}$$
(43)

When the charge is switched off (\(q=0\)), then Eqs. (40) and (41) reduce to

$$\begin{aligned}&\eta = \frac{(x+a^2) \left[ 2 a^4+x (-5+6 x)+a^2 (1+8 x)\right] +2[x-(x+a^2)^2] \sqrt{2(x+a^2)}}{\left( -1+2 a^2+2 x\right) ^2},\nonumber \\ \end{aligned}$$
(44)
$$\begin{aligned}&\xi _1 +\xi _2 = \frac{\left[ a^2 -(x+a^2)^2\right] +\left[ x-(x+a^2)^2\right] \sqrt{2(x+a^2}}{a\left( -1+2 a^2+2 x\right) }, \end{aligned}$$
(45)

which are the same as obtained for the five-dimensional Myers–Perry black holes [41].

4 Five-dimensional EMCS Black hole shadow

Higher dimensions admit astrophysical objects such as supermassive black holes, which are rather different from standard ones. The gravitational lensing features for alternative gravity theories with extra dimensions are different from general relativity [52]. Several tests were proposed to discover the signatures of extra dimensions in supermassive black holes since the gravitational field may be different from the standard one in general relativity. In particular, it was shown how measurements of the shadow can have constraints on parameters of the higher-dimensional black hole [52]. When a black hole is situated between an observer and a bright object, the light reaches the observer after being deflected by the black hole’s gravitational field; but some part of the photons emitted by the bright object ends up with falling into the black hole, and this means that photons never reach the observer.

Our aim is to calculate the boundary curve of the shadow and the existence of a photon surface around the five-dimensional EMCS black holes which is a necessary step to obtain the shadow. The incoming photons toward the black hole may follow three possible trajectories; either they fall into the black hole or they are scattered away from the black hole, and the third possibility concerns the critical geodesics that are the circular orbits around the black hole at critical radius. These are known as unstable orbits of the constant radius (located at \(r=3M\) for the Schwarzschild black hole). These are responsible for the apparent shape of the shadow of the black hole. To visualize the apparent shape of the black hole we use celestial coordinates \(\alpha \) and \(\beta \), which can be calculated by defining the orthonormal basis vectors [53] for the local observer,

$$\begin{aligned} e_{\hat{t}}= & {} \lambda e_{\text {t}} + \varsigma e_{\phi } + \chi e_{\psi }, \nonumber \\ e_{\hat{r}}= & {} \frac{1}{\sqrt{g_{rr}}} e_{\text {r}}, \quad e_{\hat{\theta }} = \frac{1}{\sqrt{g_{\theta \theta }}} e_{\theta }, \nonumber \\ e_{\hat{\phi }}= & {} \frac{1}{\sqrt{g_{\phi \phi }}} e_{\phi }, \quad e_{\hat{\psi }} = \frac{1}{\sqrt{g_{\psi \psi }}} e_{\psi }, \end{aligned}$$
(46)

where \(\lambda \), \(\varsigma \) and \(\chi \) are constants and these are chosen in such a manner that the local basis vectors are orthogonal. The coefficients in Eq. (46) are real and one can verify that \(\lbrace e_{t}, e_{r}, e_{\theta }, e_{\phi }, e_{\psi } \rbrace \) are orthonormal [53]. The basis vectors of the local observer and the basis vectors of the metric (3) are related by

$$\begin{aligned} e_{\hat{i}}= & {} e^{\mu }_{\hat{i}} e_{\mu }, \quad \hbox {and} \quad e^{\mu }_{\hat{i}} e^{\nu }_{\hat{j}} g_{\mu \nu } = \eta _{{\hat{i}} {\hat{j}}}, \end{aligned}$$
(47)

where \(\eta _{{\hat{i}} {\hat{j}}}=(-1,1,1,1,1)\). With the help of Eqs. (46) and (47) and using the orthonormality condition of the basis vectors, one can obtain the constants \(\lambda , \varsigma , \chi \) in the following form:

$$\begin{aligned} \lambda= & {} \frac{\sqrt{g_{\phi \psi }^2-g_{\phi \phi } g_{\psi \psi }}}{\sqrt{g_{tt} g_{\phi \phi } g_{\psi \psi }+2 {g_{t\phi } g_{t\psi } g_{\phi \psi }-g_{t\phi }^2 g_{\psi \psi } -g_{t\psi }^2 g_{\phi \phi } -g_{\phi \psi }^2 g_{tt}}}}, \nonumber \\ \varsigma= & {} \frac{g_{t\phi } g_{\psi \psi }-g_{t\psi } g_{\phi \psi }}{\sqrt{g_{tt} g_{\phi \phi } g_{\psi \psi }+2 {g_{t\phi } g_{t\psi } g_{\phi \psi }-g_{t\phi }^2 g_{\psi \psi } -g_{t\psi }^2 g_{\phi \phi } -g_{\phi \psi }^2 g_{tt}}}}, \nonumber \\ \chi= & {} \frac{g_{t\phi } g_{\phi \psi }-g_{t\psi } g_{\phi \phi }}{\sqrt{g_{tt} g_{\phi \phi } g_{\psi \psi }+2 {g_{t\phi } g_{t\psi } g_{\phi \psi }-g_{t\phi }^2 g_{\psi \psi } -g_{t\psi }^2 g_{\phi \phi } -g_{\phi \psi }^2 g_{tt}}}},\nonumber \\ \end{aligned}$$
(48)

where the metric components are defined in Eq. (6). Further, the contravariant components of the three-momenta in the new coordinate basis [53] are given by

$$\begin{aligned} p^{\hat{t}}= & {} \lambda E - \varsigma L_{1} - \chi L_{2}, \nonumber \\ p^{\hat{\phi }}= & {} \frac{1}{\sqrt{g_{\phi \phi }}} L_{1}, \nonumber \\ p^{\hat{\psi }}= & {} \frac{1}{\sqrt{g_{\psi \psi }}} L_{2}, \nonumber \\ p^{\hat{\theta }}= & {} \frac{p_{\theta }}{\sqrt{g_{\theta \theta }}} = \frac{\pm \sqrt{\Theta }}{\sqrt{g_{\theta \theta }}}. \end{aligned}$$
(49)

To describe the black hole shadow, we introduce the celestial coordinates [53], which in the five-dimensional black hole case takes the following form:

$$\begin{aligned} \alpha= & {} \lim _{r_{0}\rightarrow \infty } -r_{0} \frac{(p^{\hat{\phi }}+p^{\hat{\psi }})}{p^{\hat{t}}}, \nonumber \\ \beta= & {} \lim _{r_{0}\rightarrow \infty } r_{0} \frac{p^{\hat{\theta }}}{p^{\hat{t}}}. \end{aligned}$$
(50)

Here \(r_0\) is the distance from the black hole to the observer, the coordinate \(\alpha \) is the apparent perpendicular distance between the image and the axis of symmetry and the coordinate \(\beta \) is the apparent perpendicular distance between the image and its projection on the equatorial plane [41]. We take the limit \(r_0\rightarrow \infty \), since the observer is far away from the black hole. Also \(\theta _0\) is the angular coordinate of the observer or the inclination angle. Substituting the contravariant components of the three-momenta from Eq. (49) into Eq. (50), the celestial coordinates take the form

$$\begin{aligned} \alpha= & {} -\left( \xi _{1} \csc \theta _0 + \xi _{2}\sec \theta _0 \right) , \nonumber \\ \beta= & {} \pm \sqrt{\eta - \xi _{1}^2 \csc ^2 \theta _0 - \xi _{2}^2 \sec ^2 \theta _0 + a^2}. \end{aligned}$$
(51)

Interestingly, Eq. (51) has the same mathematical form as the five-dimensional Myers–Perry black hole [41] with modified impact parameters \(\eta \) and \(\xi _1 + \xi _2\) given, respectively, by Eqs. (40) and (41). However, Eq. (51) is different from the Kerr–Newman black hole [14] with additional terms due to the extra dimension. Now we consider the case when an observer is situated in the equatorial plane of the five-dimensional EMCS black hole, i.e., the inclination angle is \(\theta _0=\pi /2\). In this case, the impact parameter \(L_{\psi }=0\), therefore \(\xi _2 =0\); hence Eq. (51) transforms to

$$\begin{aligned} \alpha= & {} -\xi _1, \nonumber \\ \beta= & {} \pm \sqrt{\eta -\xi ^2_1 +a^2}. \end{aligned}$$
(52)

Similarly for \(\theta _{0}=0\). In this case \(L_{\phi }=0\) and hence \(\xi _1 =0\),

$$\begin{aligned} \alpha= & {} -\xi _2, \nonumber \\ \beta= & {} \pm \sqrt{\eta -\xi ^2_2 +a^2}. \end{aligned}$$
(53)

The shadows of a five-dimensional EMCS black hole can be visualized by plotting \(\alpha \) vs. \(\beta \) for different values of the rotation parameter (a) and the charge (q) at different inclination angles. The celestial coordinates \(\alpha \) and \(\beta \) in Eqs. (52) and (53) satisfy the relation \(\alpha ^2 + \beta ^2 = \eta + a^2\), where \(\eta \) is given by Eq. (40). It is clear that \(\alpha \) and \(\beta \) depend on the charge q and spin a.

Fig. 4
figure 4

Plot showing the shapes of black hole shadow cast by EMCS black hole with inclination angle \(\theta _0=\pi /2\) and corresponding observable \(R_{\text {s}}\), for different values of charge q for the nonrotating case (\(a=0\))

Full size image

The shadow with \(a=0\) for a five-dimensional nonrotating black hole can be obtained from

$$\begin{aligned} \alpha ^2 + \beta ^2= & {} \frac{2 -9q^2 +2 (1-3q^2)^{3/2}}{1-4q^2} \equiv r^2_{\text {s}} \quad \text {with} \quad \nonumber \\ x= & {} 1+\sqrt{(1-3q^2)}. \end{aligned}$$
(54)

The nonrotating five-dimensional EMCS black hole is a general case of the five-dimensional Reissner–Nordström black hole and its shadow appears as a perfect circle with radius \(R_{\text {s}}\) (cf. Fig. 4). We plotted the shadow of a nonrotating five-dimensional EMCS black hole for several values of charge q. The effect of the charge q can be seen by the radius of the circle with an increase in q (cf. Fig. 4). When \(q=0\), the radius of the circle of the shadow is \(R_{\text {s}}=2\), which is similar to the five-dimensional Schwarzschild black hole [42]. Thus, the effect of the charge q is to decrease the size of the shadow (cf. Fig. 4).

Fig. 5
figure 5

Plot showing the shapes of shadows cast by five-dimensional EMCS black hole with inclination angle \(\theta _0=\pi /2\) for different values of charge q and the spin a with the case \(q=0\) referring to the Myers–Perry black hole

Full size image

Next, we consider the rotating case of the five-dimensional EMCS black hole to see the behavior of black hole shadow in the presence of both spin a, charge q, and extra dimension. With increasing a, the shadow gets more and more distorted and shifts to the rightmost on the vertical axis, as in the Kerr case [51]. In the absence of charge \(q=0\), one gets

$$\begin{aligned} \alpha ^2 + \beta ^2 = \frac{(x+ a^2) \left[ 2 a^4+x (-5+6 x)+a^2 (1+8 x)\right] +2 \left( x-(x+a^2)^2\right) \sqrt{2(x+a^2)}}{(-1+2 a^2+2 x)^2}+a^2. \end{aligned}$$
(55)

The shapes of shadow for the five-dimensional EMCS black hole have been plotted in Fig. 5 for different values of the charge q and the spin a. The shape of the black hole shadow is a deformed circle instead of a perfect circle. We see that the shape of the shadow is largely affected due the parameters a, q and extra dimension. The size of the shadow decreases continuously (cf. Fig. 5) with the increase in q. This can be understood as a dragging effect due to the rotation of the black hole. The extra dimension has the same effect on the size of the shadow [41].

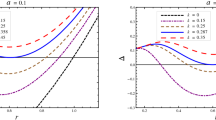
Next, it will be helpful to introduce observables which characterize the shape and the distortion of the shadow. The characterization of the observables is useful to extract more information from the black hole shadow [24]. We modify the Hioki–Maeda characterization [51] to determine the observables, radius \(R_{\text {s}}\) and distorted \(\delta _{\text {s}}\) for the rotating five-dimensional EMCS black hole [20, 51]:

$$\begin{aligned} R_{\text {s}}= & {} \frac{(\alpha _{\text {t}} - \alpha _{\text {r}})^2 + \beta _{\text {t}}^2}{2(\alpha _{\text {t}} - \alpha _{\text {r}})}, \end{aligned}$$
(56)
$$\begin{aligned} \delta _{\text {s}}= & {} \frac{{\tilde{\alpha _{\text {p}}}} -\alpha _{\text {p}}}{R_{\text {s}}}, \end{aligned}$$
(57)

where \(({\tilde{\alpha _{\text {p}}}} ,0)\) and \((\alpha _{\text {p}},0)\) are the coordinates where the reference circle and the contour of the shadow cut the horizontal axis on the opposite side of \((\alpha _{\text {r}},0)\) (cf. Fig. 6). In this characterization, the idea was that a reference circle is passing through the three coordinates of the black hole shadow. The coordinates are situated at top position (\(\alpha _{\text {t}}\), \(\beta _{\text {t}}\)), bottom position (\(\alpha _{\text {b}}\), \(\beta _{\text {b}}\)), and rightmost position (\(\alpha _{\text {r}}\), 0) (cf. Fig. 6). The behavior of the radius \(R_{\text {s}}\) and the distortion \(\delta _{\text {s}}\) with charge for different values of the spin a is depicted in Fig. 7, which suggests that the radius \(R_{\text {s}}\) monotonically decreases as q increases, and the distortion \(\delta _{\text {s}}\) of the shadow increases with q and the shadow gets more distortion for larger values of a. When compared with the five-dimensional Myers–Perry black hole [41], the effective size of the shadow decreases for higher values of the charge q. Also, a comparison with the shadow with Kerr–Newman black holes [14] indicates that the effective size of the shadow decreases due to the extra dimensions. Instead of using \(R_{\text {s}}\) and \(\delta _{\text {s}}\), one can also use the observables defined by Schee and Stuchlík [24] to arrive at the same conclusions.

5 Naked singularity

The cosmic censorship hypothesis states that the spacetime singularities are always hidden by the event horizon of the black hole [54, 55]. However, a naked singularity can be defined as a gravitational singularity in the absence of the event horizon, which leads to a violation of the cosmic censorship hypothesis [54, 55]. The cosmic censorship hypothesis has as yet no precise mathematical formulation or proof for either version and remains one of the most important unsolved problems in general relativity. Consequently, the examples that appear to violate the cosmic censorship hypothesis are important and these are useful tools for the study of this crucial issue. Recently, Figueras et al. [56] have found the strongest evidence for a violation of the weak cosmic censorship conjecture in five-dimensional spacetime. Hence, it is important to study the naked singularity shadow for the five-dimensional EMCS black hole.

Fig. 6
figure 6

Schematic representation of the observables for rotating black holes [17]

Full size image

A five-dimensional EMCS black hole admits a naked singularity, it occurs when \(\mu <(a+b)^2+2q\) or for the case of \(a=b\), \(\mu <2(2a^2+q)\). In the absence of the charge q, the condition for the existence of a naked singularity satisfies \(\mu <(a+b)^2\) (\(a \ne b\)) and \(\mu <4a^2\) (\(a=b\)). The most general condition for a naked singularity in the five-dimensional Myers–Perry spacetime is \(a>1/{\sqrt{2}}\) [41]. The shadow of the naked singularity for the five-dimensional Myers–Perry spacetime is studied in [41]. Here we plot the contour of the naked singularity shadows for different values of q and a in Fig. 8, and the shapes change dramatically as compared to black hole shadows. It is found that the shape of a naked singularity shadow forms an arc instead of a circle (cf. Fig. 8). The behavior is similar to the naked singularity in the Myers–Perry geometries [41] or in the braneworld case [20]. The unstable spherical photon orbits with a positive radius give way to an open arc instead of a closed curve due to the absence of the event horizon and photons can reach the observer. The shapes of the naked singularity shadows are affected by the charge q as well as by the spin a; its size decreases in both cases when we increase either q or a (cf. Fig. 8). Our results show that the naked singularity shadow is different from the five-dimensional Myers–Perry black hole [41] (cf. Fig. 8). We observe that the arc of the shadow tends to open with the increasing values of the spin a as well as charge q. The two observables, viz. \(R_{\text {s}}\) and \(\delta _{\text {s}}\) are no longer valid for a naked singularity and new observables are necessary.

Fig. 7
figure 7

Plots showing the variation of the radius of the black hole shadow \(R_{\text {s}}\) and distortion parameter \(\delta _{\text {s}}\) with charge q for different value of spin a

Full size image
Fig. 8
figure 8

Shadow cast by the naked singularity with inclination angle \(\theta _0=\pi /2\) for different values of the charge q and the spin a. Here Myers–Perry black hole (\(q=0\)) case is included for comparison

Full size image
Fig. 9
figure 9

Plots showing the variation of the energy emission rate with frequency \(\omega \) for different values of the charge q and the spin a for five-dimensional EMCS black holes with the case \(q=0\) referring to the Myers–Perry black hole

Full size image

6 Energy emission rate

Here, we study the energy emission rate of the five-dimensional EMCS black holes, as in the Kerr black holes [57]. It is well known that the shadow is responsible for a high energy absorption cross section due to the black hole for a far away observer [58]. The energy emission rate of a black hole can be calculated using the following relation [28, 59]:

$$\begin{aligned} \frac{{\text {d}}^2E(\omega )}{{\text {d}}\omega {\text {d}}t}= \frac{2 \pi ^2 \sigma _{{\text {lim}}}}{\exp {(\omega /T)}-1}\omega ^3, \end{aligned}$$
(58)

where \(\omega \) is the frequency, \(\sigma _{{\text {lim}}}\) is the limiting constant value for a spherically symmetric black hole around which the absorption cross section oscillates, and T is the Hawking temperature of the black hole. The Hawking temperature of the five-dimensional EMCS black hole reads [60]

$$\begin{aligned} T=\frac{{(x^{H}_{+})}^2-(a^2+q)^2}{2 \pi \sqrt{x^{H}_{+}}\left[ a^2 q +(x^{H}_{+}+a^2)^2\right] }, \end{aligned}$$
(59)

where \(x^{H}_{+}\) is the event horizon. Interestingly, the Hawking temperature (59) depends on the charge q as well as the spin a. When \(q \rightarrow 0\), the temperature reduces to

$$\begin{aligned} T = \frac{x^{H}_{+}-a^2}{2 \pi \sqrt{x^{H}_{+}} (x^{H}_{+}+a^2) }, \end{aligned}$$
(60)

which shows the temperature of the Myers–Perry black holes [61]. The limiting constant value of a five-dimensional EMCS black hole can be expressed approximately [58, 59] by

$$\begin{aligned} \sigma _{lim} \approx \pi R_{\text {s}}^3, \end{aligned}$$
(61)

where \(R_{\text {s}}\) is the radius of the black hole shadow. Hence, the complete form of the energy emission rate for a five-dimensional EMCS black hole is

$$\begin{aligned} \frac{{\text {d}}^2E(\omega )}{{\text {d}}\omega {\text {d}}t}=\frac{4\pi ^3 R_{\text {s}}^3}{e^{\omega /T}-1}\omega ^3. \end{aligned}$$
(62)

In Fig. 9, we plot the energy emission rate versus frequency \(\omega \) for different values of the charge q and the spin a. It can be seen that an increase in the values of q and a decreases the peak of energy emission rate (cf. Fig. 9). We analyze how the energy emission rate of a five-dimensional EMCS black hole decreases in comparison with a five-dimensional Myers–Perry black hole [41].

7 Conclusion

The formation of a shadow due to the strong gravitational field near a black hole has received significant attention due to a possibility of observing the images of the supermassive black hole Sgr \(A^*\) situated at the center of our galaxy [62]. The gravitational theories with extra dimensions admit black hole solutions which have different properties from the standard ones. Several tests were proposed to discover the signatures of extra dimensions in black holes as the gravitational field likely to be distinct from the one in general relativity, e.g., gravitational lensing for gravities with extra dimensions has different characteristics from general relativity. It turns out that the measurements of shadow sizes for higher-dimensional black holes can put constraints on the parameters of black holes [52], e.g., evaluating the size of a shadow it was shown that the probability to have a tidal charge (\(-q\)) for the black hole at the galactic center is ruled out by the observations [63]. Thus, it suggests that black holes with positive charge (\(+q\)) are consistent with observations, but a significant negative charge (\(-q\)) black holes is ruled out [63], i.e., the Reissner–Nordström black holes which have positive charge (\(+q\)) are consistent with the observation, but this is not true for the braneworld black holes, which have a negative tidal charge (\(-q\)). A five-dimensional EMCS black hole solution has an additional charge parameter q when compared with the five-dimensional Myers–Perry black hole, and it provides a deviation from the Myers–Perry black hole. The five-dimensional EMCS black hole has a richer configuration for the horizons and ergosphere. It is interesting to note that the ergosphere size is sensitive to the charge q as well as the rotation parameter a.

We have extended the previous studies of the black hole shadow and derived analytical formulas for the photon regions for a five-dimensional EMCS black hole. We also make quantitative analyses of the shape and size of the black hole shadow cast by a rotating five-dimensional EMCS black hole. We have analyzed how the shadow of black hole is changed due to the presence of the charge q, and we explicitly show that the charge q apparently affects the shape and the size of the shadow. In particular, it is observed that the shadow of a rotating five-dimensional EMCS black is a dark zone covered by a more deformed circle as compared to a Myers–Perry black hole shadow. For a fixed value of spin a, compared to the rotating five-dimensional Myers–Perry black hole, the size of the shadow decreases with the charge q, whereas shadows become more distorted with an increase in charge q, and the distortion is maximal for an extremal black hole. In comparison with the four-dimensional Kerr–Newman black hole, we found that the shadow of the five-dimensional EMCS black hole decreases. The study of the shadow of a naked singularity of the five-dimensional EMCS metric suggests that the shape of the shadow decreases for higher values of the charge q when compared with the naked singularity shadow with the five-dimensional Myers–Perry metric. Obviously, our results in the limit \(q\rightarrow 0\) reduce exactly to the five-dimensional Myers–Perry black hole.

We think that the results obtained here are of interest in the sense that they do offer the opportunity to explore properties associated with a shadow in higher dimensions, which may be crucial in our understanding of whether the size of the shadow might suggest if there are signatures of a five-dimensional charged black hole. The possibility of a further generalization by adding a negative cosmological constant is an interesting problem for future research under active consideration.