Quasinormal frequencies of gravitational perturbation in regular black hole spacetimes

Abstract

The quasinormal frequencies of gravitational perturbation around some well-known regular black holes were investigated in this work. We consider complete perturbations of the energy-momentum tensor of electromagnetic part for non-linear electrodynamics and gravitational field. By using the WKB approximation and the asymptotic iteration method, we make a detailed analysis of the gravitational QNM frequencies by varying the characteristic parameters of the gravitational perturbation and the spacetime charge parameters of the regular black holes. It is found that the imaginary part of quasinormal modes as a function of the charge parameter has different monotonic behaviors for different black hole spacetimes. Moreover, the asymptotic expressions of gravitational QNMs for $l \gg 1$ are obtained by using the eikonal limit method. We demonstrate that the gravitational perturbation is stable in all these spacetimes.

1 Introduction

The investigations concerning the interaction of black holes with various fields around give us the possibility to get some information about the physics of black holes. One of these information can be obtained from quasinormal modes (QNMs) which are characteristic of the background black hole spacetimes [1]. The concept of QNMs is first formulated by Vishveshwara in calculations of the scattering of gravitational waves by a black hole [2], which present complex frequencies whose real part represents the actual frequency of the oscillation and the imaginary part represents the damping. The survey of field perturbation in black hole spacetimes motivated the extensive numerical and analytical study of QNMs [5,6,7,8,9,10,11,12,13]. In addition, the properties of QNMs have been studied in the context of the AdS/CFT correspondence [14,15,16,17,18,19,20,21] and loop quantum gravity [22]. Some reviews where a lot of references to the recent research of QNMs can be found in Refs. [23, 24].

Among several types of field perturbation, gravitational perturbation is considered to be the most important one. The reason is that gravitational QNMs are important in directly identifying black holes and their gravitational radiation. Many theoretical physicists believe that the gravitational QNMs is a unique fingerprint in searching the existence of a black hole. Recently, astrophysical interests in QNMs originated from their relevance in gravitational wave analysis. On September 14th, 2015, two advanced detectors of the Laser Interferometer Gravitational-wave Observatory (LIGO) made the first direct measurement of gravitational waves [3, 4]. The Advanced LIGO detectors observed a transient gravitational-wave signal determined to be the coalescence of two black holes, launching the era of gravitational wave astronomy. The issue of black hole gravitational stability under perturbations was first addressed by Regge and Wheeler [67] in the fifties of last century. They classified gravitational perturbations into two types: odd parity and even parity by means of getting rid of the angular dependence of the perturbation variables through a tensorial generalization of the spherical harmonics, thus the calculation of gravitational perturbation was greatly simplified. The Regge-Wheeler formalism was later extended to the case of static black holes in four dimensions [25,26,27] and higher dimensions [28,29,30,31], and even to the case of rotating black holes [32, 33]. One can find a complete description of black hole perturbation theory in the book by Chandrasekhar [34].

On the other hand, the problem of understanding how to avoid singularities in black hole spacetimes is important in general relativity. In 1968, a “regular” black hole without a singularity was constructed by Bardeen [35]. This regular black hole spacetime lacked a consistent physical interpretation until Ayón-Beato and his coworkers [36] obtained this black hole solution by describing it as the gravitational field of nonlinear magnetic monopole with a mass M and a charge q in 2000.

The Bardeen solution has motivated deeper works about singularity avoidance may be realized generally. Several other researchers paid attention to theories of gravity coupled to nonlinear electrodynamics, and proposed other solutions in different contexts. Some solutions that are relevant to this work are analyzed in Refs. [37,38,39,40,41,42] and Refs. [35, 36].

Recently, there are several interesting works concerning the regular black hole. Eiroa and Sendra have investigated gravitational lensing of the regular black hole spacetime [43]. In Ref. [44], exact solutions of spherically symmetric spacetimes are proposed in f(R) modified theories of gravity coupled to nonlinear electrodynamics. The dynamical stability of black hole solutions in self-gravitating nonlinear electrodynamics with respect to linear gravitational fluctuation has been studied in [45]. Fernando and Correa have studied QNMs spectrum of the scalar field of the regular black hole for various values of the perturbation parameters [46]. They have also used the unstable null geodesics of the black hole to compute the scalar QNMs in the eikonal limit. Further research about the QNMs of neutral and charged scalar field perturbations on the regular black hole spacetime in a variety of models was carried out by Flachi and Lemos [47]. Massless and massive Dirac QNMs were studied in the regular black hole spacetime by using the WKB approach in Ref. [48].

In this paper, we concentrate on the behavior of the gravitational perturbation in the regular black hole spacetimes mentioned above. In some literatures (for instance, one can see the Ref. [49]), the authors ignore perturbations of the energy-momentum tensor of electromagnetic part for non-linear electrodynamics. Then incomplete perturbations developed in these works lead to the wrong effective potentials. Therefore, this fundamental issue disqualifies the results of their results. Therefore, We study the original article “Perturbation for gravitational and electromagnetic radiation in a Reissner–Nordström geometry” (Ref. [25]) carefully, then come to conclusion that some wavelike perturbation equations should be modified accordingly due to regular black hole spacetimes. Once the wavelike perturbation equations with an effective potential are addressed, one can solve the gravitational QNMs by several numerical methods, such as integration of the wavelike equations, the monodromy method, fit and interpolation approaches, the continued fraction method, the Mashhoon method, the WKB approximation method [50,51,52], the asymptotic iteration method [53,54,55] and so on [56,57,58,59,60,61,62,63,64,65,66]. We calculate the gravitational QNMs by using the 3rd order WKB method as well as the asymptotic iteration method.

The rest of the paper is organized as follows. In Sect. 2, we gives brief description of some well-known regular black hole spacetimes. The perturbative equation of the gravitational perturbation in given backgrounds is reduced to the Schrödinger-like wave equation in Sect. 3. The next section is devoted to the numerical calculations of the gravitational QNMs in given spacetimes by using the 3rd order WKB approximation and the asymptotic iteration method. The eikonal limit for the gravitational frequencies is also presented. The conclusions are given in last section.

2 The basic equations

In this section, we will first give a brief introduction to the regular black holes. In order to obtain the regular solutions, the typical action to include the nonlinear electrodynamic term is,

$$\begin{aligned} S = \frac{1}{16 \pi G} \int d^4x \sqrt{-g} \left( R - \mathscr {L}(F) \right) , \end{aligned}$$

(1)

where g is the determinant of the black hole metric, G is the gravitational constant, R is the scalar curvature, and $\mathscr {L}(F)$ represents the Lagrangian of the nonlinear electrodynamics with $F = \frac{1}{4}F_{\mu \nu } F^{\mu \nu }$, where $F_{\mu \nu } = \bigtriangledown _{\mu } A_{ \nu } - \bigtriangledown _{\nu } A_{ \mu }$ is the electromagnetic field strength.

The general line element for spherically symmetric regular black hole solutions can be described as

$$\begin{aligned} ds^2 = - f(r) dt^2 + \frac{dr^2}{f(r)} +r^2 d\theta ^2 + r^2\sin ^2\theta \,d\phi ^2~, \end{aligned}$$

(2)

where $(t,r,\theta ,\phi )$ are the usual space-time spherical coordinates, and specific choices of the lapse function f(r) distinguish between the different spacetimes.

In Ref. [35], the lapse function f(r) for the Bardeen black hole is determined by the formula

$$\begin{aligned} f(r) = 1-\frac{2Mr^2}{(r^2+ q^2)^{3/2}}, \end{aligned}$$

(3)

where q and M are the magnetic charge and the mass of the magnetic monopole. Ayón-Beato and his coworker interpreted this black hole as the gravitational field of a magnetic monopole arising from nonlinear electrodynamics [36]. The Lagrangian of the specific nonlinear electrodynamics is given by $\mathscr {L}(F)=(3M/|q|^3)(\sqrt{2q^2F}/(1+\sqrt{2q^2F}))^{5/2}$. The spacetime in Eq. 3 has horizons only if $|q| \le \frac{ 4 }{ 3 \sqrt{3}}$. For $q = \frac{ 4 }{ 3 \sqrt{3}}$, there are degenerate horizons. For $q > \frac{ 4 }{ 3 \sqrt{3}}$, there are no horizons.

In 2006, Hayward found new regular black hole spacetime that has center flatness and is quiet similar to the physical insight of the Bardeen one [37]. The simple regular black hole implies a specific matter energy-momentum tensor that is de Sitter at the core and vanishes at large distances $r \rightarrow \infty$. The function f(r) for the Hayward black hole also takes a simple form

$$\begin{aligned} f(r) = 1-\frac{2Mr^2}{r^3+2\alpha ^2} \end{aligned}$$

(4)

with $\alpha =$ Const. As like the Bardeen black hole, the Eq. (4) can also have zero, one, or two horizons depending on the relative values of M and $\alpha$.

Through introducing the Lagrangian for nonlinear electrodynamics to first order, the regular black hole is also constructed originally by Bronnikov [38, 39]. The lapse function for this black hole is given as

$$\begin{aligned} f=1-{2M\over r}\left( 1- \text{ tanh }{r_0\over r}\right) , \end{aligned}$$

(5)

where the parameter $r_0$ is a length scale related to the electric charge.

Then Dymnikova [40] put forward an exact, regular spherically symmetric, charged black hole solution by using the idea proposed by Bronnikov [38, 39]. This solution is constructed from a nonlinear electrodynamic theory with a Hamiltonian-like function (for more details, please see Ref. [40]). The lapse function for Dymnikova’s solution is given as

$$\begin{aligned} f(r) = 1- \frac{4M}{ \pi r} \left( \text{ tan }^{-1}{r\over r_0} - {r r_0 \over r^2+r_0^2}\right) . \end{aligned}$$

(6)

The parameter $r_0$ in the solution (6) is a length scale defined as $r_0=\pi q^2/ (8M)$, where M and q is the total mass and the charge.

Another famous regular black hole is the one presented by Ayón-Beato and García in Ref. [41]. To find this regular black hole solution, they took the nonlinear electric field as a source of charge for the solution of Maxwell field equations. Its lapse function f(r) is given as

$$\begin{aligned} f= 1-{2Mr^2\over (r^2+q^2)^{3/2}}+{q^2r^2\over (r^2+q^2)^2}~, \end{aligned}$$

(7)

where M and q are the total mass and charge. This solution can be obtained from a nonlinear electrodynamics with Lagrangian density ${\mathscr {L}}(F) = {X^2\over -2q^2}{1-8X-3X^2 \over \left( 1-X\right) ^4} -{3M\over 2 q^3 }{X^{5/2}\left( 3-2X\right) \over \left( 1-X\right) ^{7/2}}~,$ where $X=\sqrt{-2q^2F}$.

Recently Balart and Vagenas [42] built charged regular black holes in the framework of Einstein-nonlinear electrodynamics theory. They constructed the general lapse function for mass distribution functions that are inspired by continuous probability distributions. In this paper, we consider two examples of black hole solutions employing their methodology. One metric function is of the form

$$\begin{aligned} f= 1- \frac{2M}{r} e^{-\frac{q^2}{2Mr}}. \end{aligned}$$

(8)

The other metric function is written as

$$\begin{aligned} f= 1- \frac{2M}{r} \frac{2}{ \text {exp}\left( {\frac{q^2}{Mr}}\right) +1 }. \end{aligned}$$

(9)

In two metric functions M and q are associated with total mass and charge, respectively.

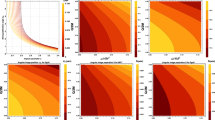
All the black hole solutions used in this paper are summarized in Table 1. The mass of black holes is normalized to 1. It is noteworthy that in all the mentioned black holes the lapse function f(r) can have zero, one, or two horizons depending on the value of charge parameters. In Table 1, we list the extreme charge parameters for which the inner horizon and outer horizon coincide. To illustrate the behavior of the lapse function more clearly, we show the lapse function as a function of r for three values of the charge parameter in Fig. 1. Noting that the plots of all lapse functions for regular black holes under consideration show similar behaviors, we take the plot of the lapse function for the Bardeen regular black hole as an example.

Table 1 Summary of some well-known regular black holes in the paper. For more details, one can refer to the Refs. [35,36,37,38,39,40,41,42] listed in the Sect. 2. In this work, the mass of black holes is normalized to 1

3 Perturbation equation for the gravitational field

The investigation of black hole perturbations was first carried out by Regge and Wheeler [67] for the odd parity type of the spherical harmonics and was extended to the even parity type by Zerilli [68].

We indicate the background metric with $g_{\mu \nu }$ and the perturbation in it with $h_{\mu \nu }$. The perturbation $h_{\mu \nu }$ is very small compared with $g_{\mu \nu }$. The $R_{\mu \nu }$ can be expressed from $g_{\mu \nu }$, and $R_{\mu \nu }+\delta R_{\mu \nu }$ from $g_{\mu \nu }+h_{\mu \nu }$. $\delta R_{\mu \nu }$ can be calculated from the form [69]

$$\begin{aligned} \delta R_{\mu \nu }=-\delta \Gamma ^{\beta }_{\mu \nu ;\>\beta }+\delta \Gamma ^{\beta }_{\mu \beta ;\>\nu }, \end{aligned}$$

(10)

where

$$\begin{aligned} \delta \Gamma ^{\alpha }_{\beta \gamma }=\frac{1}{2}g^{\alpha \nu } (h_{\beta \nu ;\>\gamma }+h_{\gamma \nu ;\>\beta }-h_{\beta \gamma ;\>\nu }). \end{aligned}$$

(11)

Fig. 1

Radial dependence of lapse function f(r) of the Bardeen regular black hole for different values of the charge parameter

The canonical form for the perturbations in the Regge-Wheeler gauge is given as [67]

$$\begin{aligned} h_{\mu \nu }= \begin{array}{|cccc|} 0&{}\quad 0&{}\quad 0&{}\quad h_{0}(r)\\ 0&{}\quad 0&{}\quad 0&{}\quad h_{1}(r)\\ 0&{}\quad 0&{}\quad 0&{}\quad 0\\ h_{0}(r)&{}\quad h_{1}(r)&{}\quad 0&{}\quad 0 \end{array}\exp (-i\omega t) \sin \theta \frac{\partial Y_{L0}}{ \partial \theta } \end{aligned}$$

(12)

Substituting Eq. (12) into Eq. (10), we get

$$\begin{aligned}&\frac{1}{f(r)}i\omega h_0(r)- \frac{d}{dr}f(r)h_1(r )= 0, \;\; \text {from} \;\; \delta R_{23}=0 \end{aligned}$$

(13)

$$\begin{aligned}&\frac{1}{f(r)} i\omega \left( i\omega h_1(r) + \frac{d}{dr}h_0(r) - \frac{2}{r}h_0(r) \right) \nonumber \\&\quad + \frac{1}{r^2}(l(l+1)-2)h_1(r) = 0, \;\; \text {from} \;\; \delta R_{13}=0 \end{aligned}$$

(14)

Defining

$$\begin{aligned} \phi = f(r)h_1(r)/r, \end{aligned}$$

(15)

then eliminating the $h_0(r)$ and following the method in Ref. [25], we get

$$\begin{aligned} \left( \frac{d^{2}}{dr_{*}^{2}}+\omega ^{2}\right) \Phi (r)= V(r) \Phi (r), \end{aligned}$$

(16)

where $r_*$ is the tortoise coordinate and

$$\begin{aligned} V(r) \!=\! f(r)\left( \frac{l(l+1)}{r^2} - 2\frac{1-f(r)}{r^2} - \frac{1}{r}\frac{df(r)}{dr} - 2 \text {L}(F) \!\right) \!. \end{aligned}$$

(17)

We should mention that perturbations of the energy-momentum tensor of electromagnetic part for non-linear electrodynamics can not be ignored. We study the article “Perturbation for gravitational and electromagnetic radiation in a Reissner–Nordström geometry” [25] carefully, which does indeed carefully retain the gauge field fluctuations in order to perform a consistent linearized analysis. Following the above reference, the Eq. (17) has been modified to incorporate the gauge field fluctuations as well. For Reissner–Nordström black hole in Einstein-Maxwell theory, the $\text {L}(F) = F = F_{\mu \nu }F ^{\mu \nu }/4, f(r) = 1- \frac{2M}{r} + \frac{q^2}{r^2}$, so $V(r) = f(r) ( \frac{l(l+1)}{r^2} -\frac{6M}{r^3} + \frac{4q^2}{r^4})$, which is consistent with Eq. (20) in original paper [25]. For details, one can refer to the Appendix in this paper.

As mentioned before, the complex $\omega$ values are written as $\omega = \text {Re}(\omega ) + i \text {Im}(\omega )$. The effective potential V(r) of wavelike perturbation equation for the black hole spacetimes is plotted to display how it changes with the angular harmonic index l in Fig. 2. One can find from Fig. 2 that the angular harmonic index l increases the height of the potential barrier governed by the effective potential.

Fig. 2

Variation of the effective potential V(r) with respect to the radial coordinate r for three values of the angular harmonic index l

4 Numerical methods and numerical results

Now we report the QNM frequencies of the gravitational perturbation in the regular black hole spacetimes. In order to calculate QNMs, boundary conditions are imposed for the wavelike perturbation equation. The boundary condition at the horizon is for the solution to be purely ingoing wave, while the other boundary condition at spatial infinity is such that the wave has to be purely outgoing one. Therefore one can write the boundary conditions as

$$\begin{aligned}&\Phi (r) \sim e^{-i\omega r_*}, \;\;\;\; \text {as} \;\;\;\; r_* \rightarrow -\infty , \end{aligned}$$

(18)

$$\begin{aligned}&\Phi (r) \sim e^{ i\omega r_*},\;\;\;\; \text {as} \;\;\;\; r_* \rightarrow +\infty . \end{aligned}$$

(19)

4.1 WKB method

The Schrödinger-like wave equation (16) with the effective potential (17) containing the lapse function f(r) related to the regular black holes is not solvable analytically. Many numerical methods are developed to compute QNMs of various black hole spacetimes in the literature. One of these standard methods is the WKB approximative method that was applied for the first time by Schutz and Will [50]. Iyer and his coworkers developed the WKB method up to third order [51] and later, Konoplya developed it up to sixth order [52]. This semianalytic method has been applied extensively in numerous black hole spacetime cases, which has been proved to be accurate up to around one percent for the real and the imaginary parts of the quasinormal frequencies for low-lying modes with $n<l$, where n is the mode number and l is the angular momentum quantum number. In this paper, the third order WKB formalism is applied since the 6th order WKB method consumes too much CPU power for some cases of regular black holes.

The 3rd order formalism of the WKB approximation presented in the paper [51] has formula

$$\begin{aligned} \frac{ \omega ^2 - V_0}{ \sqrt{ - 2 V_0^{''}}} - L_2 - L_3 = n + \frac{1}{2}. \end{aligned}$$

(20)

Here, $V_0$ and $V_0^{''}$ are the maximum potential and the second derivative of the potential evaluated at the maximum potential, n is the node number, and $L_n$ represents the n-th order correction. The formulae for $L_2$ and $L_3$ are given in [51].

4.2 The eikonal limit

It is well-know that the WKB method works with high accuracy for large values of the multipole quantum number. For $l \gg 1$, frequency of QNMs of gravitational perturbation field can be found analytically by using the first order WKB approach. Since the lapse function is complicated in any regular black hole metric, a more convenient method is used to obtain the asymptotic form of frequency of QNMs of gravitational perturbation field. For $l \gg 1$, the effective potential V(r) at its maximum has a asymptotic form: $V(r_{Max}) \propto l(l+1)$. Then the QNM frequency takes the form

$$\begin{aligned} \lim _{l \rightarrow \infty } \omega \approx c_1\left( l+\frac{1}{2}\right) -i c_2\left( n+\frac{1}{2}\right) \ . \end{aligned}$$

(21)

We can readily fix $c_1$ and $c_2$ by setting $l \gg 1$ in numerical calculations. In Table 2, we list different $c_1$ and $c_2$ for several regular black hole spacetimes.

Table 2 The constant $c_1$ and $c_2$ in the eikonal limit for given regular black hole spacetimes

4.3 The asymptotic iteration method

The asymptotic iteration method (AIM) was first applied to solve the second order differential equations [70]. This new method was then used to obtain the QNM frequencies of field perturbation in Schwarzschild black hole spacetime  [53].

Let’s consider a second order differential equation of the form

$$\begin{aligned} \chi ''=\lambda _{0}(x)\chi '+s_{0}(x)\chi , \end{aligned}$$

(22)

where $\lambda _{0}(x)$ and $s_{0}(x)$ are well defined functions and sufficiently smooth. Differentiating the equation above with respect to x leads to

$$\begin{aligned} \chi '''=\lambda _{1}(x)\chi '+s_{1}(x)\chi , \end{aligned}$$

(23)

where the new two coefficients are $\lambda _{1} (x) =\lambda _{0}'+s_{0}+\lambda _{0}^{2}$ and $s_{1}(x)=s_{0}'+s_{0}\lambda _{0}.$

Using this process iteratively, we can get the $(n+2)$-th derivative of $\chi (x)$ with respect to x as

$$\begin{aligned} \chi ^{(n+2)}=\lambda _{n}(x)\chi '+s_{n}(x)\chi , \end{aligned}$$

(24)

where the new coefficients $\lambda _{n}(x)$ and $s_{n}(x)$ are associated with the older ones through the following relation

$$\begin{aligned} \lambda _{n}(x)=\lambda '_{n-1}+s_{n-1}+\lambda _{0}\lambda _{n-1}, \;\;\;\; s_{n}(x)=s'_{n-1}+s_{0}\lambda _{n-1}. \end{aligned}$$

(25)

For sufficiently large values of n, the asymptotic concept of the AIM method is introduced by  [54],

$$\begin{aligned} \frac{s_{n}(x)}{\lambda _{n}(x)}=\frac{s_{n-1}(x)}{\lambda _{n-1}(x)} = \text {Constant}. \end{aligned}$$

(26)

The perturbation frequencies can be obtained from the above “quantization condition”. However this procedure has a difficulty in that the process of taking the derivative of $\lambda _{n}(x)$ and $s_{n}(x)$ terms of the previous iteration at each step can consume much time and affect the numerical precision of calculations. To overcome these drawbacks, $\lambda _{n}(x)$ and $s_{n}(x)$ are expanded in Taylor series around the point $x'$ at which the AIM method is performed [53],

$$\begin{aligned} \lambda _{n}(x')=\sum _{i=0}^{\infty }c_{n}^{i}(x- x')^{i}&,&s_{n}(x')=\sum _{i=0}^{\infty }d_{n}^{i}(x-x')^{i}, \end{aligned}$$

(27)

where $c_{n}^{i}$ and $d_{n}^{i}$ are the i-th Taylor coefficients of $\lambda _{n}(x')$ and $s_{n}(x')$, respectively. Substitution of above equations into Eq. (25) leads to a set of recursion relations for the Taylor coefficients as

$$\begin{aligned} c^{i}_{n}= & {} \sum _{k=0}^{i}c_{0}^{k}c_{n-1}^{i-k} + (i+1)c_{n-1}^{i+1}+ d^i_{n-1} ,\nonumber \\ d_n^i= & {} \sum _{k=0}^{i}d_{0}^{k}c_{n-1}^{i-k} + (i+1)d^{i+1}_{n-1}. \end{aligned}$$

(28)

Table 3 The gravitational QNMs in the Bardeen black hole spacetime as a function of the charge parameter. As comparison, we also calculate the QNMs in the Reissner–Nordström black hole spacetime. The numerical results are computed by the AIM method. Here, $n=0$ and $l = 2$

After applying the recursion relations (28) in Eq. (26), the quantization condition then can be expressed as

$$\begin{aligned} d_{n}^{0}c_{n-1}^{0}- c_{n}^{0} d_{n-1}^{0}=0, \end{aligned}$$

(29)

which can be employed to calculate the QNMs of a black hole. Both the accuracy and efficiency of the AIM method are greatly improved without any derivative computation [53].

First, we calculate gravitational QNM frequencies by varying the charge of the Bardeen regular black hole. We also calculate the gravitational QNM frequencies for the Reissner–Nordström black hole with the same charge for comparison as shown in Table 3. Here, the node number $n=0$ and the angular momentum quantum number $l = 2$. From Table 3, it is shown clearly that the real part $\text {Re}(\omega )$ of the gravitational QNMs increases when charge parameter q increases for the two black hole spacetimes. And the imaginary value $\text {Im}(\omega )$ of QNMs decreases for the Bardeen black hole spacetime with q, while for the Reissner–Nordström black hole spacetime, the imaginary value arrives a maximum 0.0930 around $q = 0.76$.

Table 4 QNMs for gravitational perturbations for $q=$ 0.1, 0.3, 0.6 for the model of Refs. [35, 36]

Table 5 QNMs for gravitational perturbations for $\alpha = 0.1, 0.4, 0.7$ for the model of Refs. [37]

Table 6 QNMs for gravitational perturbations for $\alpha = 0.1, 0.3, 0.4$ for the model of Refs. [38, 39]. The parameter $r_0$ is a length scale related to the charge

Table 7 QNMs for gravitational perturbations for $\alpha = 0.1, 0.3, 0.4$ for the model of Refs. [40]

Table 8 QNMs for gravitational perturbations for $q = 0.0, 0.3, 0.6$ for the model of Refs. [41]

Table 9 QNMs for gravitational perturbations for $q = 0.1, 0.3, 0.6$ for the first model of Refs. [42]

Table 10 QNMs for gravitational perturbations for $q = 0.1, 0.3, 0.6$ for the second model of Refs. [42]

Results for the quasinormal frequencies for gravitational perturbations in regular black hole spacetimes under consideration are tabulated, in Table 4 for the solution given in Refs. [35, 36], in Table 5 for the solution given in Ref. [37], in Table 6 for the solution given in Ref. [38, 39], in Table 7 for the solution given in Ref. [40], in Table 8 for the solution given in Ref. [41], in Table 9 for the solution given in Ref. [42], and in Table 10 for the solution given in Ref. [42]. The values of the quasinormal frequencies listed in these tables are computed by the third order WKB method (without parenthesis) and the AIM method (with parenthesis), respectively. It has been shown that the linear perturbative gravitational field are stable around all of the considered regular black holes.

We can apply the sixth order WKB approximation to check the convergence of the WKB approximation. In Fig. 3, The real and imaginary parts of the QNMs from gravitational perturbations for the $l = 2, n = 0$ mode for the model of Bardeen [35] are presented when higher order terms in the WKB approximation are included in the computation. It shows that the accuracy of the third order WKB method is reliable.

The above calculations have shown that increasing of the spacetime charge parameter implies monotonic increasing of the real part of quasinormal frequency. However, the imaginary part of quasinormal frequency as a function of the charge parameter has different monotonic behaviors for different black hole spacetimes.

For the Bardeen spacetime, the Hayward spacetime and the solution of Ref. [41], increasing of the spacetime charge parameter implies monotonic decreasing of the imaginary part of QNM frequency; For the two solutions of Ref. [42], the imaginary part of QNM frequency increases when the charge parameter increases; However, for the two solutions of Refs. [38,39,40], there exists a maximum of the imaginary part in the charge parameter interval.

Fig. 3

Re($\omega$) and Im($\omega$) parts of the gravitational QNMs of the Bardeen black hole with $q=0.1$ as a function of WKB order are given for the $n=0, \;\; l=2$ and $n=0, \;\; l=2$ modes

5 Summary

Although we do not have a complete theory of quantum gravity, regular black hole solutions were proposed by coupling Einstein gravity to an external form of matter. Therefore it is interesting to compute QNMs for the regular black hole spacetimes and see how it is different from the ordinary ones. In this work, we have studied the quasinormal modes of gravitational perturbation around some well-known regular black hole by using the WKB approximation and the asymptotic iteration method. Through numerical calculation, we made a detailed analysis of the gravitational QNM frequencies by varying the characteristic parameters of the gravitational perturbation and the spacetime charge parameters of the regular black holes. Numerical results show that the imaginary part of quasinormal modes as a function of the charge parameter has different monotonic behaviors for different black hole spacetimes. The asymptotic expressions of gravitational QNMs for $l \gg 1$ are computed by using the eikonal limit method. It is demonstrated that the gravitational perturbation is stable in all these spacetimes.

Appendix

As mentioned in Sect. 1, some literatures ignore perturbations of the energy-momentum tensor of electromagnetic part for non-linear electrodynamics. Therefore, incomplete perturbations developed in these works lead to the wrong effective potentials. We study the article “Perturbation for gravitational and electromagnetic radiation in a Reissner–Nordström geometry” carefully, then come to conclusion that for the case of regular black hole spacetimes some equations in this article should be modified accordingly:

The last three equations of Page 861 in this article should be modified as

$$\begin{aligned} \delta E_{\mu \nu }^{(h)}= & {} - \frac{1}{4\pi } \left[ g^{\rho \alpha }g^{\sigma \beta }\left( F_{\rho _\mu } F_{\sigma _\nu }- \frac{1}{2}g_{\mu \nu }g^{k\lambda }F_{\rho k} F_{\sigma \lambda } \right) \right. \nonumber \\&\left. \times \text {L}(F) h_{\alpha \beta } + \frac{1}{4} \text {L}(F) h_{\mu \nu }\right] , \end{aligned}$$

(A1)

$$\begin{aligned} \delta E_{\mu \nu }^{(f)}= & {} \frac{1}{4\pi } \bigg [g^{\rho \sigma }(F_{\sigma _\nu } f_{\rho _\mu } + F_{\sigma \mu }f_{\rho \nu } )\nonumber \\&-\, F_{\sigma \mu } F^\sigma _\nu \delta \text {L}(F) - \frac{1}{2}g_{\mu \nu } g^{\alpha \rho } g^{\beta \sigma }F_{\alpha \beta }f_{\rho \sigma }\bigg ], \end{aligned}$$

(A2)

$$\begin{aligned} 4\pi (-g)^{\frac{1}{2}}j^\mu= & {} \bigg [(-g)^{\frac{1}{2}} ( g^{\nu \beta }g^{\mu \rho }g^{\alpha \sigma } + g^{\mu \alpha }g^{\nu \rho }g^{\beta \sigma } )F_{\alpha \beta }h_{\rho \sigma } \text {L}(F)\nonumber \\&-\, \frac{1}{2} (-g)^{\frac{1}{2}} g^{\mu \alpha }g^{\nu \beta } F_{\alpha \beta }\text {L}(F) h\bigg ]_{\nu }, \end{aligned}$$

(A3)

And the Eqs. (16), (17) and (19) in this article should be modified as:

$$\begin{aligned}&-\omega ^2 e^{-\nu }h_1 + i \omega e^{-\nu } \frac{ dh_0}{dr} - \frac{2i\omega }{r} e^{-\nu } h_0 + e^{\nu } \left( \nu ^{''} + \nu ^{'2} + \frac{2\nu '}{r} \right) h_1\nonumber \\&\quad +\, 2\lambda r^{-2} h_1 = 2 \text {L}(F) h_1 - 4F_{10} e^{-\nu } \tilde{f}_{02} + A_{12}, \end{aligned}$$

(A4)

$$\begin{aligned}&-\, e^{\nu } \frac{ d^2 h_0}{d^2r} - i \omega e^{\nu } \frac{ dh_1}{dr} - \frac{2i\omega }{r} h_1 + e^{\nu } \left( \nu ^{''} + \nu ^{'2} + \frac{2\nu '}{r} + \frac{2}{r^2} \right) h_0 \nonumber \\&\quad + 2\lambda r^{-2} h_0 = 2\text {L}(F) h_0 - 4F_{10} e^{\nu } \tilde{f}_{12} + A_{02}, \end{aligned}$$

(A5)

$$\begin{aligned}&e^{\nu } \frac{d}{dr} e^{\nu } \frac{ \tilde{f}_{23} }{dr} + \omega ^2 \tilde{f}_{23} - \frac{L(L+1)}{r^2} e^{\nu } \tilde{f}_{23} \nonumber \\&\quad = \text {L}(F) F_{10} L(L+1)e^{\nu } \left( i \omega h_1 + r^2 \frac{d}{dr} \frac{h_0}{r^2}\right) - 4\pi L(L+1)e^{\nu }y,\nonumber \\ \end{aligned}$$

(A6)

Then, the equation in (20) is modified as

$$\begin{aligned}&\frac{d^2 R^{(m)}_{LM}}{dr^{*2}}+ \omega ^2 R^{(m)}_{LM} - e^\nu \bigg [ \frac{(L-1)(L+2)}{r^2} \nonumber \\&\qquad +\, e^\nu \left( \frac{2}{r^2} + {\nu ^{'}}^2 + \nu ^{''}+\frac{\nu ^{'}}{r} \right) -2\text {L}(F)\bigg ] R^{(m)}_{LM}\nonumber \\&\quad = \frac{4i\omega }{r}F_{10} e^{\nu } f^{(m)}_{LM} - \frac{e^{2\nu }}{r} A_{12} + \frac{1}{2} r e^\nu { \frac{d}{dr} \left( \frac{e^\nu }{r^2}A_{22}\right) }, \end{aligned}$$

(A7)

By using the relation $e^{\nu } = f(r)$, an effective potential of the wavelike perturbation equation is obtained as

$$\begin{aligned} V(r) = f(r) \left( \frac{L(L+1)}{r^2} - 2 \frac{1-f(r)}{r^2} - \frac{1}{r}\frac{df(r)}{dr} - 2 \text {L}(F)\right) \end{aligned}$$

(A8)

For Reissner–Nordström black hole in Einstein-Maxwell theory, the $\text {L}(F) = F = F_{\mu \nu }F ^{\mu \nu }/4, f(r) = 1- \frac{2M}{r} + \frac{e^2}{r^2}$, so

$$\begin{aligned} V(r) = f(r) \left( \frac{L(L+1)}{r^2} -\frac{6M}{r^3} + \frac{4q^2}{r^4 } \right) , \end{aligned}$$

(A9)

which is consistent with the result in original paper.