1 Introduction

Over a few decades, relativistic astrophysics have gone through extensive developments, following the discovery of high energy phenomena in the universe such as gamma ray bursts. Compact objects like neutron stars have interesting physical properties, where the effect of strong gravity fields and hence general relativity are seen to play a fundamental role. A similar situation, involving a strong gravitational field, is that of a massive star undergoing a continual gravitational collapse at the end of its life cycle. This collapse phenomenon, dominated by the force of gravity, is fundamental in black hole physics and has received increasing attention in the past decades. The first systematic analysis of gravitational collapse in general relativity was given in 1939 by Oppenheimer and Snyder [1]. In this context, we also refer to the work by Datt [2]. Later developments in the study of gravitational collapse have been comprehensively summarized by Joshi [3, 4].

Scalar fields have been of great interest in theories of gravity for various reasons. A scalar field with a variety of potential can fit superbly for cosmological requirements such as playing the role of the driver of the past or the present accelerated expansion of the universe. Apart from cosmological aspect, a suitable scalar potential can often mimic various matter distribution, including fluids with different equations of state.

Collapsing models with scalar fields are also quite well studied in general relativity. The collapse of a zero mass scalar field was discussed by Christodoulou in [5]. Subsequently, the possibility of the formation of a naked singularity as an end product of a scalar field collapse has also been explored in [6]. Some variants of scalar field collapse and its implications are studied in [7,8,9,10,11,12,13,14,15,16,17] (see also [18,19,20,21,22,23]).

It is well known that the Einstein–Hilbert action can be generalized by adding higher order curvature terms which naturally arise from diffeomorphism property of the action. Such terms also have their origin in string theory from quantum corrections. In this context F(R) [24,25,26,27,28], Gauss–Bonnet (GB) [24, 25, 29,30,31,32,33] or more generally Lanczos–Lovelock [34,35,36] gravity are some of the candidates in higher curvature gravitational theory. The spacetime curvature inside a collapsing star gradually increases as the collapse continues and becomes very large near the final state of the collapse. Thus, for a collapsing geometry where the curvature becomes very large near the final state of the collapse, the higher curvature terms are expected to play a crucial role. Motivated by this idea, the collapsing scenarios in the presence of F(R) gravity have been recently discussed by Goswami et al. [37] and by Chakrabarti and Banerjee [38, 39].

In the present context, we take the route of Gauss–Bonnet gravity to investigate the role of the higher order curvature in a scalar field collapse in four dimension. The advantage of Gauss–Bonnet gravity is that the equations of motion do not contain any higher derivative terms (higher than two) of the metric, which lead to ghost free solution. The particular questions that we address in this paper are the following:

  1. 1.

    Is the scalar field collapse possible in the presence of Gauss–Bonnet gravity?

  2. 2.

    If such a collapsing scenario is found, what is then the end product of the collapse, a black hole or a naked singularity?

In order to address the above questions, we consider a “scalar-Einstein–Gauss–Bonnet” theory [40] where the scalar field is coupled non-minimally to the GB term. The equations in a relativistic theory of gravity is already highly nonlinear and the presence of the Gauss–Bonnet terms makes the situation even more difficult. In order to make the equations tractable, we start with a spatially homogeneous and isotropic model, i.e., essentially a Friedmann model. Except the scalar field, we do not consider any other matter such as a fluid, but the collapse is homogeneous and thus somewhat analogous to the Oppenheimer–Snyder collapse [1].

Our paper is organized as follows. In Sect. 2, we describe the model. In Sect. 3, we obtain the exact solution for the metric. Sects. 4 and 5 address the visibility of the singularity produced as a result of the collapse and a matching of the solution with an exterior spacetime, respectively. We end the paper with some concluding remarks in Sect. 6.

2 The model

To explore the effect of Gauss–Bonnet gravity on scalar field collapse, we consider a “scalar-Einstein–Gauss–Bonnet” theory in four dimension where the Gauss–Bonnet (GB) term is coupled with the scalar field. This coupling with the scalar field ensures the non-topological character of the GB term. The action for this model is given by

$$\begin{aligned} S= & {} \int \mathrm{d}^4x \sqrt{-g} \bigg [\frac{R}{2\kappa ^2} - \frac{1}{2}g^{\mu \nu }\partial _{\mu }\Phi \partial _{\nu }\Phi \nonumber \\&- V(\Phi )-\xi (\Phi )G\bigg ], \end{aligned}$$
(1)

where g is the determinant of the metric, R is the Ricci scalar, \(1/(2\kappa ^2)=M_{p}^2\) is the four dimensional squared Planck mass, \(G=R^2-4R_{\mu \nu }R^{\mu \nu }+R_{\mu \nu \alpha \beta } R^{\mu \nu \alpha \beta }\) is the GB term, \(\Phi \) denotes the scalar field also endowed with a potential \(V(\Phi )\). The coupling between scalar field and GB term is symbolized by \(\xi (\Phi )\) in the action. Variation of the action with respect to metric and scalar field leads to the field equations:

$$\begin{aligned}&\frac{1}{\kappa ^2} [-R^{\mu \nu }+\frac{1}{2}g^{\mu \nu }R] + \frac{1}{2}\partial ^{\mu }\Phi \partial ^{\nu }\Phi - \frac{1}{4}g^{\mu \nu }\partial _{\rho }\Phi \partial ^{\rho }\Phi \nonumber \\&\qquad + \frac{1}{2}g^{\mu \nu }\big [-V(\Phi )+\xi (\Phi )G\big ]\nonumber \\&\qquad - 2\xi (\Phi )RR^{\mu \nu } - 4\xi (\Phi )R^{\mu }_{\rho }R^{\nu \rho } - 2\xi (\Phi )R^{\mu \rho \sigma \tau }R^{\nu }_{\rho \sigma \tau } \nonumber \\&\qquad + 4\xi (\Phi )R^{\mu \rho \nu \sigma }R_{\rho \sigma }\nonumber \\&\qquad + 2[\nabla ^{\mu }\nabla ^{\nu }\xi (\Phi )]R - 2g^{\mu \nu }[\nabla ^2\xi (\Phi )]R \nonumber \\&\qquad - 4[\nabla _{\rho }\nabla ^{\mu }\xi (\Phi )]R^{\nu \rho } - 4[\nabla _{\rho }\nabla ^{\nu }\xi (\Phi )]R^{\mu \rho }\nonumber \\&\qquad + 4[\nabla ^2\xi (\Phi )]R^{\mu \nu } + 4g^{\mu \nu }[\nabla _{\rho }\nabla _{\sigma }\xi (\Phi )]R^{\rho \sigma } \nonumber \\&\qquad + 4[\nabla _{\rho }\nabla _{\sigma }\xi (\Phi )]R^{\mu \rho \nu \sigma } = 0 \end{aligned}$$
(2)

and

$$\begin{aligned} g^{\mu \nu }[\nabla _{\mu }\nabla _{\nu }\Phi ] - V'(\Phi ) - \xi '(\Phi )G = 0, \end{aligned}$$
(3)

where a prime denotes the derivative with respect to \(\Phi \). It may be noticed that the gravitational equation of motion does not contain any derivative of the metric components of order higher than two.

The aim here is to construct a continual collapse model and for this purpose, we consider the following spherically symmetric non-static metric ansatz for the interior:

$$\begin{aligned} \mathrm{d}s^2 = -\mathrm{d}t^2 + a^2(t)\big [\mathrm{d}r^2 + r^2\mathrm{d}\theta ^2 + r^2\sin ^2{\theta }\mathrm{d}\varphi ^2\big ] , \end{aligned}$$
(4)

where the factor a(t) solely governs the interior spacetime characterized by the coordinates t, r, \(\theta \) and \(\varphi \). For such metric, the expression of Ricci scalar R and GB term G take the following form:

$$\begin{aligned} R= & {} 6[2H^2 + \dot{H}]\\ G= & {} 24H^2[H^2 + \dot{H}] \end{aligned}$$

with \(H=\dot{a}/a\) and a dot denotes the derivative with respect to time (t). Using the metric presented in Eq. (4), the field equations can be simplified and turn out to be

$$\begin{aligned}&-(3/\kappa ^2)H^2 + (1/2)\dot{\Phi }^2 + V(\Phi ) + 24H^3\dot{\xi } = 0, \end{aligned}$$
(5)
$$\begin{aligned}&\quad \frac{1}{\kappa ^2}\big [2\dot{H}+3H^2\big ] + (1/2)\dot{\Phi }^2 - V(\Phi ) - 8H^2\ddot{\xi } \nonumber \\&\qquad - 16H\dot{H}\dot{\xi } - 16H^3\dot{\xi } = 0, \end{aligned}$$
(6)

and

$$\begin{aligned} \ddot{\Phi } +3H\dot{\Phi } + V'(\Phi ) + 24\xi '(\Phi )(H^4+H^2\dot{H}) = 0. \end{aligned}$$
(7)

To derive these equations, we consider the scalar field to be homogeneous in space. It is evident that due to the presence of GB term, cubic and quartic powers of H(t) appear in the above equations.

It is well known that Einstein–Gauss–Bonnet gravity in four dimensions reduces to standard Einstein gravity; the additional terms actually cancel each other. In the present case, the non-minimal coupling with the scalar field assists the contribution from the GB term survive [40]. It is easy to see, in all the field equations above, that a constant \(\xi \) (essentially no coupling) would immediately make the GB contribution trivial.

3 Exact solutions: collapsing models

In this section, we present a possible analytic solution of the field equations (Eqs. (5), (6) and (7)) and in order to do this, we consider a string inspired model [40] with

$$\begin{aligned} V(\Phi ) = V_0 e^{-\sqrt{3} \kappa \Phi } \end{aligned}$$

and

$$\begin{aligned} \xi (\Phi ) = \xi _0 e^{\sqrt{3} \kappa \Phi }, \end{aligned}$$
(8)

where \(V_0\) and \(\xi _0\) are constants. With these forms of \(V(\Phi )\) and \(\xi (\Phi )\), Eqs. (5), (6) and (7) turn out be

$$\begin{aligned}&-(3/\kappa ^2)H^2 + (1/2)\dot{\Phi }^2 + V_0 e^{-\sqrt{3} \kappa \Phi } \nonumber \\&\qquad + 24\sqrt{3}\kappa \xi _0H^3e^{\sqrt{3} \kappa \Phi }\dot{\Phi } = 0, \end{aligned}$$
(9)
$$\begin{aligned}&\frac{1}{\kappa ^2}\big [2\dot{H}+3H^2\big ]+(1/2)\dot{\Phi }^2 - V_0 e^{-\sqrt{3} \kappa \Phi }\nonumber \\&\qquad - 8\sqrt{3} \kappa \xi _0H^2e^{\sqrt{3} \kappa \Phi }\big (\ddot{\Phi }+\sqrt{3} \kappa \dot{\Phi }^2\big )\nonumber \\&\quad - 16\sqrt{3} \kappa \xi _0H\dot{H}e^{\sqrt{3} \kappa \Phi }\dot{\Phi } - 16\sqrt{3} \kappa \xi _0H^3e^{\sqrt{3} \kappa \Phi }\dot{\Phi } = 0,\nonumber \\ \end{aligned}$$
(10)

and

$$\begin{aligned} \ddot{\Phi }+ & {} 3H\dot{\Phi } - \sqrt{3} \kappa V_0 e^{-\sqrt{3} \kappa \Phi } \nonumber \\+ & {} 24\sqrt{3} \kappa \xi _0e^{\sqrt{3} \kappa \Phi }\big (H^4+H^2\dot{H}\big ) = 0, \end{aligned}$$
(11)

respectively. Here we are interested on the collapsing solutions where the radius of the two sphere ra(t) decreases monotonically with time. Keeping this in mind, the above three equations (Eqs. (9), (10), (11)) are solved for H(t), \(\Phi (t)\) and the solutions are as follows:

$$\begin{aligned} H(t) = -\frac{p}{(t_0 - t)}, \end{aligned}$$
(12)

and

$$\begin{aligned} \Phi (t) = \frac{2}{\sqrt{3} \kappa }\ln {\bigg [\frac{1}{\kappa }\big (t_0 - t\big )\bigg ]}, \end{aligned}$$
(13)

where \(t_0\) is a constant of integration and the constant p is related to \(V_0\) and \(\xi _0\) through the following two relations:

$$\begin{aligned}&-3\frac{p^2}{\kappa ^2} + \frac{2}{3\kappa ^2} + V_0\kappa ^2 + 48p^3\xi _0/\kappa ^2 = 0, \end{aligned}$$
(14)
$$\begin{aligned}&-\frac{2p}{\kappa ^2} + \frac{2}{3\kappa ^2} + V_0\kappa ^2 - 24p^3(p-1)\xi _0/\kappa ^2 = 0. \end{aligned}$$
(15)

From the above relations, it can easily be shown that in the absence of the coupling parameter \(\xi _0\) (i.e., if \(\xi _0=0\)), p takes the value as \(p=\frac{2}{3}\). Therefore, this particular value of the power exponent p (\(=\frac{2}{3}\)) is not possible in the present context where the spacetime geometry evolves in the presence of “Gauss–Bonnet” term. However, by substituting \(V_0\) from Eqs. (14) to (15), one can express the parameter p in terms of \(\xi _0\) as follows:

$$\begin{aligned} p - \frac{2}{3} = 8\xi _0 p^2(p+1). \end{aligned}$$
(16)

Clearly \(p=\frac{2}{3}\) when \(\xi _0\) becomes zero. Therefore in order to better understand the deviation of the present model from the usual Einstein-scalar theory (i.e \(\xi _0=0\)), we construct a perturbative expansion of p in powers of \(\xi _0\) by using Eq. (16). Up to the second order in \(\xi _0\), such an expansion of p takes the following form:

$$\begin{aligned} p = \frac{2}{3} + \frac{160}{27}\xi _0 + 126 \xi _0^2. \end{aligned}$$
(17)

Hence the presence of Gauss–Bonnet coupling takes the parameter p away from the value \(\frac{2}{3}\). Stronger the Gauss–Bonnet coupling, more the deviation of p from 2 / 3.

Equation (12) immediately leads to the evolution of scale factor a(t):

$$\begin{aligned} a(t) = a_0(t_0 - t)^p, \end{aligned}$$
(18)

where \(a_0\) is an integration constant. The expression of a(t) (see Eq. (18)) clearly reveals that ra(t) decreases monotonically with time for \(p > 0\). Therefore, the volume of the sphere of scalar field collapses with time and goes to zero at \(t\rightarrow t_0\), giving rise to a finite time zero proper volume singularity. It is interesting to note that without the non-minimal coupling, the solution reduces to the time-reversed standard spatially flat Friedmann solution for a dust distribution (pressure \(=0\)), here the solution is contracting rather than expanding.

In order to investigate whether the singularity is a curvature singularity or just an artifact of coordinate choice, one must look into the behavior of Kretschmann curvature (K) scalar at \(t\rightarrow t_0\). For the metric presented in Eq. (4), K has the following expression:

$$\begin{aligned} K = 6\bigg [\frac{\ddot{a}(t)^2}{a(t)^2} + \frac{\dot{a}(t)^4}{a(t)^4}\bigg ]. \end{aligned}$$
(19)

Using the solution of a(t) (see Eq. (18)), the above expression of K can be simplified to

$$\begin{aligned} K = 6p^2\bigg [(p-1)^2 + p^2\bigg ]\frac{1}{\big (t_0 - t\big )^4}. \end{aligned}$$
(20)

It is clear from Eq. (20) that the Kretschmann scalar diverges at \(t\rightarrow t_0\) and thus the collapsing sphere discussed here ends up in a curvature singularity.

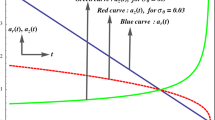
From Eq. (18), we obtain the plot (Fig. 1) between a(t) and t for two different values of p.

Fig. 1
figure 1

a(t) vs. t for various values of p

Full size image

Figure 1 clearly demonstrates that the spherical body collapses with time almost uniformly until t approaches a value close to \(t_0\), where it hurries towards a zero proper volume singularity. This qualitative behavior is almost not affected by different choices of p, only the rates of the changes. We have presented here two specific examples with \(p=0.5\) and \(p=0.2\).

4 Visibility of the singularity

Whether the curvature singularity is visible to an exterior observer depends on the formation of an apparent horizon. The condition for such a surface is given by

$$\begin{aligned} g^{\mu \nu } Z_{,\mu } Z_{,\nu }\bigg |_{r_{ah},t_{ah}} = 0 \end{aligned}$$
(21)

where Z is the proper radius of the two sphere, given by ra(t) in the present case, \(r_{ah}\) and \(t_{ah}\) being the comoving radial coordinate and time of formation of the apparent horizon, respectively. Using the form of \(g^{\mu \nu }\) presented in Eq. (4), the above expression can be simplified and turns out to be

$$\begin{aligned} r_{ah}^2 \dot{a}(t_{ah})^2 = 1 \end{aligned}$$
(22)

Due to the solution of a(t), Eq. (22) takes the following form:

$$\begin{aligned} \big [t_0 - t_{ah}\big ]^{2p-2} = \frac{1}{(r_{ah}^2 a_0^2 p^2)}. \end{aligned}$$
(23)

The above expression clearly reveals that \(t_{ah}\) is less than \(t_0\) (i.e. \(t_{ah} < t_0\)). Therefore the apparent horizon forms before the formation of singularity. Thus, the curvature singularity discussed here is always covered from an exterior observer by the formation of an apparent horizon. It may be mentioned that the singularity is independent of the radial coordinate r and it is covered by a horizon. This result is consistent with the result obtained by Joshi et al. [41] that unless one has a central singularity, it cannot be a naked singularity.

5 Matching of the interior spacetime with an exterior geometry

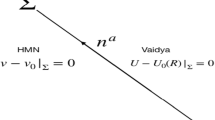
To complete the model, the interior spacetime geometry of the collapsing sphere needs to be matched to an exterior geometry. For the required matching, the Israel conditions are used, where the metric coefficients and extrinsic curvatures (first and second fundamental forms, respectively) are matched at the boundary of the sphere. Following references [17, 42], we match the interior spacetime with a generalized Vaidya exterior spacetime at the boundary hypersurface \(\Sigma \) given by \(r = r_0\). The metrics inside and outside of \(\Sigma \) are given by

$$\begin{aligned} \mathrm{d}s_{-}^2 = -\mathrm{d}t^2 + a^2(t)\bigg [\mathrm{d}r^2 + r^2\mathrm{d}\theta ^2 + r^2\sin ^2{\theta }\mathrm{d}\varphi ^2\bigg ] \end{aligned}$$
(24)

and

$$\begin{aligned} \mathrm{d}s_{+}^2= & {} -\bigg (1 - \frac{2M(r_v,v)}{r_v}\bigg )\mathrm{d}v^2 + 2\mathrm{d}v\mathrm{d}r_v + r_v^2\mathrm{d}\theta ^2\nonumber \\&+ r_v^2\sin ^2{\theta }d\varphi ^2, \end{aligned}$$
(25)

respectively, where \(r_v,v,\theta \) and \(\varphi \) are the exterior coordinates and \(M(r_v,v)\) is known as generalized mass function. The same hypersurface \(\Sigma \) can alternatively be defined by the exterior coordinates as \(r_v = R(t)\) and \(v = T(t)\). Then the metrics on \(\Sigma \) from the inside and outside coordinates turn out to be

$$\begin{aligned} \mathrm{d}s_{-,\Sigma }^2 = -\mathrm{d}t^2 + a^2(t)r_0^2 \mathrm{d}\Omega ^2 \end{aligned}$$

and

$$\begin{aligned} \mathrm{d}s_{+,\Sigma }^2 = -\bigg [\bigg (1 - \frac{2M_{\Sigma }(t)}{R(t)}\bigg )\dot{T}^2 - 2\dot{T}\dot{R}\bigg ]\mathrm{d}t^2 + R(t)^2 \mathrm{d}\Omega ^2 \end{aligned}$$

where \(M_{\Sigma }(t)\) (\(=M(R(t),T(t))\)) is the generalized mass function on \(\Sigma \), \(\mathrm{d}\Omega ^2\) denotes the line element on a unit two sphere and dot represents \(\frac{\mathrm{d}}{\mathrm{d}t}\). Matching the first fundamental form on \(\Sigma \) (i.e. \(\mathrm{d}s_{-,\Sigma }^2 = \mathrm{d}s_{+,\Sigma }^2\)) yields the following two conditions:

$$\begin{aligned} \frac{\mathrm{d}T(t)}{\mathrm{d}t} = \frac{1}{\sqrt{1 - \frac{2M_{\Sigma }(t)}{R(t)} - 2\frac{\mathrm{d}R(t)}{\mathrm{d}T(t)}}} \end{aligned}$$
(26)

and

$$\begin{aligned} R(t)= & {} r_0a(t)\nonumber \\= & {} r_0a_0 (t_0 - t)^{p} \end{aligned}$$
(27)

In order to match the second fundamental form, we calculate the normal of the hypersurface \(\Sigma \) from inside (\(\vec {n}_{-} = n_{-}^t\), \(n_{-}^r\), \(n_{-}^{\theta }\), \(n_{-}^{\varphi }\)) and outside (\(\vec {n}_{+} = n_{+}^v\), \(n_{+}^{r_v}\), \(n_{+}^{\theta }\), \(n_{+}^{\varphi }\)) coordinates as follows:

$$\begin{aligned} n_{-}^t = 0, \quad n_{-}^r = a(t), \quad n_{-}^{\theta } = n_{-}^{\varphi } = 0, \end{aligned}$$
(28)

and

$$\begin{aligned} n_{+}^v= & {} \frac{1}{\sqrt{1 - \frac{2M_{\Sigma }(t)}{R(t)} - 2\frac{\mathrm{d}R(t)}{\mathrm{d}T(t)}}},\nonumber \\ n_{+}^{r_v}= & {} \frac{1 - \frac{2M_{\Sigma }(t)}{R(t)} - \frac{\mathrm{d}R(t)}{\mathrm{d}T(t)}}{\sqrt{1 - \frac{2M_{\Sigma }(t)}{R(t)} - 2\frac{\mathrm{d}R(t)}{\mathrm{d}T(t)}}},\nonumber \\&n_{+}^{\theta } = n_{+}^{\varphi } = 0. \end{aligned}$$
(29)

The above expressions of \(\vec {n}_{-}\) and \(\vec {n}_{+}\) lead to the extrinsic curvature of \(\Sigma \) from interior and exterior coordinates, respectively, and they are given by

$$\begin{aligned} K_{tt}^- = 0,\quad K_{\theta \theta }^- = r_0a(t), \quad K_{\varphi \varphi }^- = r_0a(t)\sin ^2{\theta }, \end{aligned}$$
(30)

from the interior metric, and

$$\begin{aligned} K_{tt}^+= & {} \frac{\partial M_{\Sigma }(t)}{\partial R(t)} - \frac{M_{\Sigma }(t)}{r_0a(t)} - r_0^2 a(t)\ddot{a}(t), \nonumber \\ K_{\theta \theta }^+= & {} R(t) \frac{1 - \frac{2M_{\Sigma }(t)}{R(t)} - \frac{dR(t)}{dT(t)}}{\sqrt{1 - \frac{2M_{\Sigma }(t)}{R(t)} - 2\frac{dR(t)}{dT(t)}}}~~, \nonumber \\ K_{\varphi \varphi }^+= & {} R(t)\sin {\theta }^2 \frac{1 - \frac{2M_{\Sigma }(t)}{R(t)} - \frac{dR(t)}{dT(t)}}{\sqrt{1 - \frac{2M_{\Sigma }(t)}{R(t)} - 2\frac{dR(t)}{dT(t)}}}, \end{aligned}$$
(31)

from the exterior metric.

The equality of the extrinsic curvatures of \(\Sigma \) from both sides is therefore equivalent to the following two conditions:

$$\begin{aligned} r_0 a(t) = R(t) \frac{1 - \frac{2M_{\Sigma }(t)}{R(t)} - \frac{\mathrm{d}R(t)}{\mathrm{d}T(t)}}{\sqrt{1 - \frac{2M_{\Sigma }(t)}{R(t)} - 2\frac{\mathrm{d}R(t)}{\mathrm{d}T(t)}}} \end{aligned}$$
(32)

and

$$\begin{aligned} \frac{\partial M_{\Sigma }(t)}{\partial R(t)} = \frac{M_{\Sigma }(t)}{r_0a(t)} + r_0^2 a(t)\ddot{a}(t) \end{aligned}$$
(33)

By using Eqs. (26), (27) and (32), the mass function on \(\Sigma \) (i.e. \(M_{\Sigma }(t)\)) can be determined and is given by

$$\begin{aligned} M_{\Sigma }(t)= & {} \frac{1}{2} R(t)\dot{R}^2(t)\nonumber \\&\propto (t_0 - t)^{3p-2}\nonumber \\&\propto \rho a^3(t) \end{aligned}$$
(34)

where \(\rho \) (\(= \frac{1}{2}\dot{\Phi }^2 + V(\Phi )\)) is energy density of the scalar field \(\Phi \). Moreover, with Eqs. (26) and (34), one finally ends with the following expression:

$$\begin{aligned} \frac{dT(t)}{dt} = \frac{1}{\big (1 + r_0a_0 p(t_0 - t)^{p-1}\big )}. \end{aligned}$$
(35)

Equations (27), (33), (34) and (35) completely specify the matching at the boundary of the collapsing scalar field with an exterior generalized Vaidya geometry. However, all the matching conditions are not independent, but Eq. (33) can be derived from the other three conditions.

One important point, to be noted from Eq. (23), is that the horizon radius \(r_{ah}\) is independent of \(r_0\), which is the radial coordinate defining the separation between the interior and the exterior of the collapsing object. It also deserves mention that a horizon, if it forms, is outside the private content of the collapsing star, and the actual boundary of the matter content of the star is completely obscure for an observer outside the horizon.

At this stage, it deserves mention that the interior spacetime is matched with exterior “Schwarzschild geometry” for the only possible value of the parameter ’p’ i.e. \(p = \frac{2}{3}\). But as discussed earlier, for this particular value of p the Gauss–Bonnet coupling parameter (\(\xi _0\)) goes to zero, which in turn annihilates the GB term from the action. Thus in the present context, the presence of Gauss–Bonnet gravity spoils the matching of interior geometry of the collapsing cloud with an exterior Schwarzschild geometry. This is quite consistent because the presence of Gauss–Bonnet term generates an effective energy momentum tensor which cannot be zero (since it arises effectively from spacetime curvature) at the outside of \(\Sigma \) and hence no exterior vacuum like Schwarzschild solution is matched with the interior spacetime metric in the presence of the Gauss–Bonnet term.

6 Conclusion

We consider a “scalar-Einstein–Gauss–Bonnet” theory in four dimensions where the scalar field couples non-minimally with the Gauss–Bonnet term. This coupling with the scalar field ensures the non topological character of the GB term. In this scenario, we examine the possibility of collapse of the scalar field by considering a spherically symmetric spacetime metric.

With the aforementioned metric, an exact solution is obtained for the spacetime geometry, which clearly reveals that the radius of a two sphere decreases monotonically with time if the parameter p is taken to be greater than zero. This parameter p is actually determined by the strength of the coupling of the scalar field to the GB term and a parameter (\(V_0\)) by the relations (14) and (15).

From the behaviour of Kretschmann scalar, it is found that the singularity formed as a result of the collapse is a finite time curvature singularity. Moreover, the scalar field energy density also seems to be divergent at the singularity. The formation of apparent horizon is investigated and it turns out that the apparent horizon forms before the formation of singularity. Therefore the curvature singularity discussed here is hidden from exterior by an apparent horizon.

Finally, we match the interior spacetime geometry of the collapsing sphere with generalized Vaidya exterior geometry at the boundary of the cloud (\(\Sigma \)). For this matching, the Israel junction conditions are used where the metric coefficients and extrinsic curvatures are matched on \(\Sigma \). We determine the matching conditions given in Eqs. (27), (33), (34) and (35). We also investigate whether the interior geometry can be matched with a Schwarzschild exterior geometry or not. It is found that the interior spacetime is matched with the exterior Schwarzschild for the only possible value of ‘p’ as \(p = \frac{2}{3}\). But for this particular value of p (\(=\frac{2}{3}\)), the Gauss–Bonnet coupling parameter (\(\xi _0\)) goes to zero which in turn vanishes the GB term from the action. Thus in the present context, the presence of Gauss–Bonnet gravity spoils the matching of interior geometry of the collapsing cloud with an exterior Schwarzschild geometry. This result is in fact quite consistent because the presence of Gauss–Bonnet term generates an effective energy momentum tensor which cannot be zero (since it arises effectively from spacetime curvature) at the outside of \(\Sigma \) and hence no exterior vacuum like Schwarzschild solution is matched with the interior spacetime metric in the presence of Gauss–Bonnet term.

Another important point to be mentioned that the singularity formed is not a central singularity, it is formed at any value of r within the distribution. Such a singularity in general relativity is always covered by a horizon [41]. It is interesting to note that the result obtained in the present work in the presence of Gauss–Bonnet term is completely consistent with the corresponding GR result.