Abstract
The newly-discovered \(\Xi _{cc}^{++}\) decays into the \( \Lambda _{c}^+ K^-\pi ^+\pi ^+\), but the experimental data has indicated that this decay is not saturated by any two-body intermediate state. In this work, we analyze the multi-body weak decays of doubly heavy baryons \(\Xi _{cc}\), \(\Omega _{cc}\), \(\Xi _{bc}\), \(\Omega _{bc}\), \(\Xi _{bb}\) and \(\Omega _{bb}\), in particular the three-body nonleptonic decays and four-body semileptonic decays. We classify various decay modes according to the quark-level transitions and present an estimate of the typical branching fractions for a few golden decay channels. Decay amplitudes are then parametrized in terms of a few SU(3) irreducible amplitudes. With these amplitudes, we find a number of relations for decay widths, which can be examined in future.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Nowadays Lattice QCD is the sole approach that can study nonperturbative strong interactions from first principle. Despite the fact that there have been great progresses on Lattice QCD, hadron structures are still often encoded by phenomenological approaches like quark models or QCD sum rules. The quark model can be used to classify the hadrons, in which a baryon is assigned as a three-quark system. Among various baryonic states, doubly heavy baryons are of particular interest since they provide a platform to study the nonperturbative dynamics in the presence of heavy quarks. These states have been searched for a long time [1,2,3,4,5,6], and in 2017 the LHCb collaboration has announced an observation of the \(\Xi _{cc}^{++}(ccu)\) with the mass \( m_{\Xi _{cc}^{++}} = (3621.40\pm 0.72\pm 0.27\pm 0.14) \mathrm{MeV}\) [7]. This analysis is based on the 1.7 \(fb^{-1}\) data accumulated at 13 TeV, and confirmed in the additional sample of data collected at 8 TeV.
By all means the observation of \(\Xi _{cc}^{++}(ccu)\) is a milestone in hadron physics on both theoretical and experimental sides. One would anticipate that more experimental data on production and decays of doubly heavy baryons will be released based on the larger data sample to be collected by LHCb in future [8]. On the other side, to reveal the internal structures of doubly heavy baryons, more detailed theoretical efforts are needed [9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25].
To handle weak decays of heavy mesons, factorization approach is widely adopted in order to separate high-energy and low-energy degrees of freedoms. High-energy contributions are calculable using the ordinary perturbation theory. The low-energy degrees, or equivalently the long-distance contributions, are usually parameterized as low energy inputs such as light-cone distribution amplitudes. In terms of heavy baryon decays, neither the low-energy inputs nor the short-distance coefficients are available in the literature. Only recently the “decay constants” were studied in QCD sum rules [26].
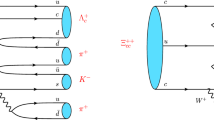
This work is an extension of a series of previous works [10, 11, 14, 24, 26]. In Ref. [14], instead of factorization, we have adopted the flavor SU(3) symmetry and classified various decays of doubly heavy baryons. In that work, however, we have limited ourselves to two-body nonleptonic decay modes. The \(\Xi _{cc}^{++}\) baryon has been firstly observed in the mode \(\Xi _{cc}^{++} \rightarrow \Lambda _{c}^+ K^-\pi ^+\pi ^+\) [7], and experimental data has indicated that this mode is not saturated by two-body intermediate state. This motivates us to study the multi-body decays. The main objective of this work is to do so, and we will focus on the cases where the final states contain one additional light meson, namely three-body nonleptonic decay and four-body semileptonic decays.
The rest of this paper is organized as follows. In Sect. 2, we will collect representations for the particle multiplets in the SU(3) symmetry. In Sect. 3, we will give a list of golden channels that can be used to reconstruct the doubly heavy baryons, and we present an estimate of their branching fractions. In Sect. 4, we will analyze the semileptonic decays of the doubly-heavy baryons, in which the final state contains two hadrons. The three-body nonleptonic decays of doubly-charmed baryons, doubly-bottom baryons and the baryons with b, c quarks are investigated in Sects. 5, 6 and Sect. 7, respectively. The last section contains a brief summary.
2 Particle multiplets
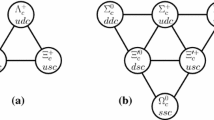
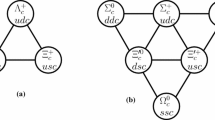
In this section, we start with the representations for the multiplets of the flavor SU(3) group. Quantum numbers of the doubly heavy baryons are derived from the quark model. These baryons can form an SU(3) triplet:
The light baryons form an SU(3) octet and a decuplet. The octet has the expression:
and the light decuplet is given as
In the meson sector, the light pseudo-scalar meson is an octet, which can be represented as:
and we shall not consider the flavor singlet \(\eta _1\) in this work. This is also applicable to the vector meson octet and other light mesons.
Charmed baryons form an anti-triplet or sextet:
Charmed mesons forms an SU(3) anti-triplet:
The above classification is also applicable to bottom mesons.
3 Golden decay channels
Before presenting the decay amplitudes for various channels, we will make a list of the golden channels and give an estimate of the decay branching fractions in this section [10]. In the following list we give, a hadron is generic and can be replaced by the states with the same quark structure, for instance one can replace \(\overline{K}^0\) by \(\overline{K}^{*0}\) which decays into \(K^-\pi ^+\). Since the \(\pi ^0, \eta \), \(\rho ^+\) (decaying into \(\pi ^+\pi ^0\)), and \(\omega \) (mainly decaying into \(\pi ^+\pi ^-\pi ^0\)) are difficult to reconstruct at LHC, we have removed the modes involving these hadrons.
3.1 \(\Xi _{cc}\) and \(\Omega _{cc}\)
The Feynman diagrams for the Cabibbo-allowed decays are given in Fig. 1. We only show one type of penguin diagrams. The \(C,C', B,E\) diagrams are suppressed by \(1/N_c\) compared to the tree amplitude T. For the \(\Xi _{cc}\) and \(\Omega _{cc}\) decays, we collect Cabibbo allowed decays in Table 1. From the D and \(\Lambda _c\) decay data, we infer that these Cabibbo allowed decay channels have typical branching fractions at a few percent level.
3.2 \(\Xi _{bc}\) and \(\Omega _{bc}\)
A list of possible modes to reconstruct the bcq baryons is given in Table 2. For the charm quark decay, the typical branching fractions might be a few percents. The final state contains either a bottom meson, or a bottom baryon, whose decay branching fraction is then at the order \(10^{-3}\). So the branching fraction to reconstruct the \(\Xi _{bc}\) and \(\Omega _{bc}\) is very likely at the order \(10^{-5}\).
If the bottom quark decay first in the bcq baryons, the branching fraction might be even smaller than \(10^{-3}\), since the total width of \(\Xi _{bc}\) and \(\Omega _{bc}\) is dominated by charm quark decay. In this case, the branching fraction to reconstruct \(\Xi _{bc}\) and \(\Omega _{bc}\) might be even smaller than \(10^{-5}\).
3.3 \(\Xi _{bb}\) and \(\Omega _{bb}\)
The channels that can be used to reconstruct the \(\Xi _{bb}\) and \(\Omega _{bb}\) are collected in Table 3. Their typical branching fractions are at the order \(10^{-3}\). However in order to reconstruct the bottom meson and bottom baryons in the final state, the price to pay is another factor of \(10^{-3}\). Including the fraction for \(J/\psi \) or D or charmed baryons, we have the largest decay branching fraction for \(\Xi _{bb}\) and \(\Omega _{bb}\) at the order of \(10^{-8}\).
4 Semi-Leptonic decays
4.1 \(\Xi _{cc}\) and \(\Omega _{cc}\) decays
The \(c\rightarrow q\bar{\ell }\nu \) transition is induced by the effective Hamiltonian:
where \(q=d,s\) and the \(V_{cd}\) and \(V_{cs}\) are CKM matrix elements. The heavy-to-light quark operators will form an SU(3) triplet, denoted as \(H_{ 3}\) with the components \((H_{ 3})^1=0,~(H_{ 3})^2=V_{cd}^*,~(H_{ 3})^3=V_{cs}^*\). At the hadron level, the effective Hamiltonian for decays of \(\Xi _{cc}\) and \(\Omega _{cc}\) into a singly charmed baryon and a light meson is constructed as:
Here the \(a_i\) are SU(3) irreducible amplitudes.
The decay amplitudes for different channels can be deduced from the Hamiltonian in Eq. (8), and given in Table 4. The channels with the CKM factor \(V_{cs}\) can have branching fractions about a few percents, while the \(c\rightarrow d\) induced channels have the branching fractions at the order of \(10^{-3}\). From these amplitudes, we can find the relations for decay widths in the SU(3) symmetry limit. For decays into a singly charmed baryon (anti-triplet), we have
Relations for decays into a singly charmed baryon (sextet) are given as:
4.2 Semileptonic \(\Xi _{bb}\) and \(\Omega _{bb}\) decays
The b quark decay is governed by the electro-weak Hamiltonian
with \(q'=u,c\). The \(b\rightarrow c\) transition is an SU(3) singlet, while the \(b\rightarrow u\) transition forms an SU(3) triplet \(H_{3}'\) with \((H_3')^1=1\) and \((H_3')^{2,3}=0\). The hadron level Hamiltonian for semileptonic \(\Xi _{bb}\) and \(\Omega _{bb}\) decays is constructed as
The decay amplitudes can be deduced from this Hamiltonian, and the results are given in Table 5.
For decays into a bcq, we have the relations for decay widths
For \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a singly bottom baryon, we have the relations for decay widths:
4.3 Semileptonic \(\Xi _{bc}\) and \(\Omega _{bc}\) decays
For the charm quark decays in \(\Xi _{bc}\) and \(\Omega _{bc}\), one can obtain the decay amplitudes from those for \(\Xi _{cc}\) and \(\Omega _{cc}\) decays with the replacement of \(T_{cc}\rightarrow T_{bc}\), \(T_c\rightarrow T_b\) and \(D\rightarrow B\). For the bottom quark decay, one can obtain them from those for \(\Xi _{bb}\) and \(\Omega _{bb}\) decays with \(T_{bb}\rightarrow T_{bc}\), \(T_b\rightarrow T_c\) and \(B\rightarrow D\). Thus we do not repeat the tedious results here.
5 Non-Leptonic \(\Xi _{cc}\) and \(\Omega _{cc}\) decays
Usually the charm quark decays into light quarks are classified into three groups: Cabibbo allowed, singly Cabibbo suppressed, and doubly Cabibbo suppressed:
Under the flavor SU(3) symmetry, the tree operators like \(\bar{s}c \bar{u}d\) transform as \(\mathbf{3}\otimes \bar{\mathbf{3}}\otimes \mathbf{3}=\mathbf{3}\oplus \mathbf{3}\oplus \bar{\mathbf{6}}\oplus \mathbf{{15}}\). So the hadron-level Hamiltonian can be decomposed in terms of a vector \((H_3)\), a traceless tensor antisymmetric in upper indices, \(H_\mathbf{\overline{6}}\), and a traceless tensor symmetric in upper indices, \(H_\mathbf{{15}}\). As we will show in the following, the representation \(H_3\) will vanishes from the unitarity of CKM matrix.
For the \(c\rightarrow s u \bar{d}\) transition, we have the nonzero matrix element:
while for the doubly Cabibbo suppressed transition \(c\rightarrow d u \bar{s}\), we have
For the transition \(c\rightarrow u \bar{d}d\), we have
with all other remaining entries zero. The overall CKM factor is \(V_{cd}^*V_{ud} \simeq -\sin (\theta _C)\). While for the transition \(c\rightarrow u \bar{s}s\), we have
with all other remaining entries zero. The overall CKM factor is \(V_{cs}^*V_{us} \simeq \sin (\theta _C)\). Since the CKM factors for \(c\rightarrow u \bar{d}d\) and \(c\rightarrow u \bar{s}s\) are almost equal in magnitudes, we combine the two transitions. Thus the singly Cabibbo-suppressed channel has the following hadron-level Hamiltonian:
5.1 Decays into a charmed baryon and two light mesons
With the above expressions, one may derive the effective Hamiltonian for decays involving the anti-triplet heavy baryons as
For the sextet baryon, we have the Hamiltonian
We have checked that the \(\overline{b}_{1}\) and \(\overline{b}_{9}\) terms give the same contribution as the \(b_1\) and \(b_9\), and the corresponding amplitudes always contain the factor \(b_1-\overline{b}_{1}\) for anti-triplet and \(b_9-\overline{b}_{9}\) for sextet. So we can remove \(\overline{b}_{1}\) and \(\overline{b}_{9}\) term in the expanded amplitude.
It should be mentioned that the dynamical mechanisms of these terms are not all the same. For the production of final two light mesons, some terms contain one QCD coupling while the others contain two QCD couplings. Expanding the above equations, we will obtain the decay amplitudes given in Tables 6, 7 for the anti-triplet baryon and Tables 8, 9, 10 for the sextet. Based on the expanded amplitudes, we derive the relations for decay widths collected in Appendix A 1.
5.2 Decays into a light baryon, a charmed meson and a light meson
The hadron-level Hamiltonian for the decays of \(T_{cc}\) into a light octet baryon, a charmed meson and a light meson is given as
Expanding the above equations, we will obtain the decay amplitudes given in Tables 11, 12 and 13. This leads to the relations for decay widths: in Appendix A 2.
For a light decuplet in the final state, the Hamiltonian is given as
The corresponding decay amplitudes are given in Table 14, and it leads to the relations for decay widths also collected in Appendix A 2.
6 Non-Leptonic \(\Xi _{bb}\) and \(\Omega _{bb}\) decays
For the bottom quark decay, there are generically four kinds of quark-level transitions:
with \(q_{1,2,3}\) as a light quark. Each of them can induce more than one types of decay modes at hadron level, which will be discussed in order.
6.1 \(b\rightarrow c\bar{c} d/s\): decays into \(J/\psi \), a bottom baryon and a light meson
These decays have the same topology with semileptonic \(b\rightarrow s\ell ^+\ell ^-\) decays, and thus the SU(3) relations derived in this subsection are also applicable to semileptonic \(b\rightarrow s\ell ^+\ell ^-\) decays. The transition operator \(b\rightarrow c\bar{c}d/s\) can form an SU(3) triplet, which leads to the effective Hamiltonian:
with \((H_{ 3})_{2}=V_{cd}^*\) and \((H_{ 3})_{3}=V_{cs}^*\). Decay amplitudes are given in Table 15, from which we derive the relations for decay widths: Appendix A 3.
6.2 \(b\rightarrow c\bar{c} d/s\): decays into a doubly heavy baryon bcq, an anti-charmed meson and a light meson
The \(b\rightarrow c\bar{c}d/s\) transition can induce another type of effective Hamiltonian:
This Hamiltonian denotes the decays into doubly heavy baryon bcq plus an anti-charmed meson. Decay amplitudes are given in Table 16. Thus we obtain the following relations for decay widths: Appendix A 4.
6.3 \(b\rightarrow c \bar{u} d/s\) transition: decays into a doubly heavy baryon bcq plus two light mesons
The operator to produce a charm quark from the b-quark decay, \(\bar{c} b \bar{q} u\), is given by
The light quarks in this effective Hamiltonian form an octet with the nonzero entry \( (H_{\mathbf{8}})^2_1 =V_{ud}^* \) for the \(b\rightarrow c\bar{u}d\) transition, and \((H_{\mathbf{8}})^3_1 =V_{us}^*\) for the \(b\rightarrow c\bar{u}s\) transition. The hadron-level effective Hamiltonian is then given as
Decay amplitudes are expanded in Table 17, which leads to the relations: Appendix A 5.
6.4 \(b\rightarrow c \bar{u} d/s\) transition: decays into a bottom baryon bqq, a charmed meson and a light meson
The effective Hamiltonian from the operator \(\bar{c} b \bar{q} u\) gives
Results are given in Table 18 for anti-triplet and Table 19 for sextet, thus we have the relations for decay amplitudes: Appendix A 6 for sextet. Actually, for the anti-triplet case there’s no definite relations between the decay withs.
6.5 \(b\rightarrow u \bar{c} d/s\): decays into a bottom baryon bqq plus anti-charmed meson and a light meson
For the anti-charm production, the operator having the quark contents \((\bar{u}b)(\bar{q}c)\) is given by
The two light anti-quarks form the \( \bar{\mathbf{3}}\) and \(\mathbf{6}\) representations. The anti-symmetric tensor \(H_{\bar{3}}''\) and the symmetric tensor \(H_{ 6}\) have nonzero components \( (H_{\bar{3}}'')^{13} =- (H_{\bar{3}}'')^{31} =V_{cs}^*\), \( (H_{\bar{6}})^{13}=(H_{\bar{6}})^{31} =V_{cs}^*, \) for the \(b\rightarrow u\bar{c}s\) transition. For the transition \(b\rightarrow u\bar{c}d\) one requests the interchange of \(2\leftrightarrow 3\) in the subscripts, and \(V_{cs}\) replaced by \(V_{cd}\).
The effective Hamiltonian is constructed as
Decay amplitudes for different channels are given in Tables 20 and 21. We derive relations for decay amplitudes given in Appendix A 7.
The \(\Xi _{bb}\) can decay into both \( D^0\) and \( D^0\). The \(D^0\) and \(\overline{D}^0\) can form the CP eigenstates \(D_{+}\) and \(D_-\). Thus using the \(\Xi _{bb}\) decays into the \( D_\pm \), one may construct the interference between the \(b\rightarrow c\bar{u}s\) and \(b\rightarrow u\bar{c}s\). The CKM angle \(\gamma \) can then be extracted from measuring decay widths of these channels, as in the case of \(B\rightarrow DK\) [27,28,29,30,31,32], \(B\rightarrow DK^*_{0,2}\) [33, 34] and others. This is also similar for the \(\Omega _{bb}\rightarrow D_\pm \) decays and the following \(\Xi _{bc}\rightarrow D_\pm \) and \(\Omega _{bc}\rightarrow D_{\pm }\) channels.
6.6 Charmless \(b\rightarrow q_1 \bar{q}_2 q_3\) decays: decays into a bottom baryon and two light mesons
The charmless \(b\rightarrow q\) (\(q=d,s\)) transition is controlled by the weak Hamiltonian \({\mathcal {H}}_{eff}\):
where \(O_{i}\) is a four-quark operator or a moment type operator. At the hadron level, penguin operators behave as the \(\mathbf{3}\) representation while tree operators can be decomposed in terms of a vector \(H_\mathbf{3}\), a traceless tensor antisymmetric in upper indices, \(H_\mathbf{\overline{6}}\), and a traceless tensor symmetric in upper indices, \(H_\mathbf{{15}}\). For the \(\Delta S=0 (b\rightarrow d)\)decays, the non-zero components of the effective Hamiltonian are [35,36,37]:
and all other remaining entries are zero. For the \(\Delta S=1(b\rightarrow s)\) decays the nonzero entries in the \(H_\mathbf{{3}}\), \(H_\mathbf{\overline{6}}\), \(H_\mathbf{{15}}\) are obtained from Eq. (30) with the exchange \(2\leftrightarrow 3\).
The effective hadron-level Hamiltonian for decays into the bottom anti-triplet is constructed as
while for the sextet baryon, we have
There also exists an extra term with irreducible amplitude \(\overline{c}_{5}\). We will remove this term since it always appears in the amplitude in the form of \(c_5-\overline{c}_{5}\). Decay amplitudes for different channels are given in Tables 22, 24 and 25 for \(b\rightarrow d\) transition; Tables 23, 26 and 27 for \(b\rightarrow s\) transition. Thus, it leads to the relations for decay widths given in Appendix A 8.
6.7 Charmless \(b\rightarrow q_1 \bar{q}_2 q_3\) decays: decays into a bottom meson, a light baryon octet and a light meson
The effective Hamiltonian is given as
Decay amplitudes for different channels are given in Tables 28 and 29 for \(b\rightarrow d\) transition; Tables 30 and 31 for \(b\rightarrow s\) transition respectively.
6.8 Charmless \(b\rightarrow q_1 \bar{q}_2 q_3\) Decays: Decays into a bottom meson, a light baryon decuplet and a light meson
The effective Hamiltonian is given as
Decay amplitudes for different channels are given in Tables 32 and 33 for \(b\rightarrow d\) transition; Tables 34 and 35 for \(b\rightarrow s\) transition. We summarize the corresponding relations for decay widths in Appendix A 9.
7 Non-Leptonic \(\Xi _{bc}\) and \(\Omega _{bc}\) decays
Decays of \(\Xi _{bc}\) and \(\Omega _{bc}\) can proceed via the b quark decay or the c quark decay. As we have shown in the semileptonic channels, for the charm quark decays, one can obtain the decay amplitudes from those for \(\Xi _{cc}\) and \(\Omega _{cc}\) decays with the replacement of \(T_{cc}\rightarrow T_{bc}\), \(T_c\rightarrow T_b\) and \(D\rightarrow B\). For the bottom quark decay, one can obtain them from those for \(\Xi _{bb}\) and \(\Omega _{bb}\) decays with \(T_{bb}\rightarrow T_{bc}\), \(T_b\rightarrow T_c\) and \(B\rightarrow D\). Thus we do not present the tedious results again.
8 Conclusions
Quite recently, the LHCb collaboration has observed the \(\Xi _{cc}^{++}\) in the final state \(\Lambda _c K^-\pi ^+\pi ^+\). Such an important observation will undoubtedly promote the research on both hadron spectroscopy and weak decays of doubly heavy baryons.
In this paper, we have analyzed weak decays of doubly heavy baryons \(\Xi _{cc}\), \(\Omega _{cc}\), \(\Xi _{bc}^{(\prime )}\), \(\Omega _{bc}^{(\prime )}\), \(\Xi _{bb}\) and \(\Omega _{bb}\) under the flavor SU(3) symmetry, where the final states involve one or two light mesons. This is inspired by the experimental fact that the \(\Xi _{cc}^{++}\rightarrow \Lambda _c K^-\pi ^+\pi ^+\) is not dominated by any two-body intermediate state. Decay amplitudes for various semileptonic and nonleptonic decays have been parametrized in terms of a few SU(3) irreducible amplitudes. We have found a number of relations or sum rules between decay widths, which can be examined in future measurements at experimental facilities like LHC [8], Belle II [38] and CEPC [39]. On the one hand, at first sight the number of relations is desperately large. On the other hand, once a few decay branching fractions were measured in future, these relations can provide richful important clues for the exploration of other decay modes.
It should be stressed that our analysis in this work using the flavor SU(3) symmetry is only applicable to non-resonant contributions. For a complete exploration of three-body decays, one should also take into account resonant contributions from two-body states and this has been given in Ref. [14]. Relative phases between them can be obtained in a Dalitz plot analysis or measurements of invariant mass distributions. In addition, SU(3) symmetry breaking effects might also be relevant. Such effects in the phase space can be incorporated once masses of all involved hadrons are known. This will remedy the relations for decay widths we derived. Actually, we have removed the channels kinematically prohibited. Further deviations, if found by experimentalists in future, would have the indications on decay dynamics in the doubly heavy baryon system. We hope this analysis together with experimental measurements in future will help to establish a QCD-rooted approach to handle the production and decays of doubly heavy baryons.
References
M. Mattson et al. [SELEX Collaboration], Phys. Rev. Lett. 89, 112001 (2002). https://doi.org/10.1103/PhysRevLett.89.112001. arXiv:hep-ex/0208014
A. Ocherashvili et al. [SELEX Collaboration], Phys. Lett. B 628, 18 (2005). https://doi.org/10.1016/j.physletb.2005.09.043. arXiv:hep-ex/0406033
Y. Kato et al. [Belle Collaboration], Phys. Rev. D 89(5), 052003 (2014). https://doi.org/10.1103/PhysRevD.89.052003. arXiv:1312.1026 [hep-ex]
R. Aaij et al. [LHCb Collaboration], JHEP 1312, 090 (2013). https://doi.org/10.1007/JHEP12(2013)090. arXiv:1310.2538 [hep-ex]
B. Aubert et al. [BaBar Collaboration], Phys. Rev. D 74, 011103 (2006). https://doi.org/10.1103/PhysRevD.74.011103. arXiv:hep-ex/0605075
S. P. Ratti, Nucl. Phys. Proc. Suppl. 115, 33 (2003). https://doi.org/10.1016/S0920-5632(02)01948-5
R. Aaij et al. [LHCb Collaboration], Phys. Rev. Lett. 119(11), 112001 (2017). https://doi.org/10.1103/PhysRevLett.119.112001. arXiv:1707.01621 [hep-ex]
R. Aaij et al. [LHCb Collaboration], Eur. Phys. J. C 73(4), 2373 (2013). https://doi.org/10.1140/epjc/s10052-013-2373-2. arXiv:1208.3355 [hep-ex]
H. X. Chen, Q. Mao, W. Chen, X. Liu, S. L. Zhu, Phys. Rev. D 96(3), 031501 (2017). https://doi.org/10.1103/PhysRevD.96.031501. arXiv:1707.01779 [hep-ph]
F. S. Yu, H. Y. Jiang, R. H. Li, C. D. Lü, W. Wang, Z. X. Zhao, arXiv:1703.09086 [hep-ph]
W. Wang, F. S. Yu, Z. X. Zhao, Eur. Phys. J. C 77(11), 781 (2017). https://doi.org/10.1140/epjc/s10052-017-5360-1. arXiv:1707.02834 [hep-ph]
H. S. Li, L. Meng, Z. W. Liu, S. L. Zhu, Phys. Rev. D 96(7), 076011 (2017). https://doi.org/10.1103/PhysRevD.96.076011. arXiv:1707.02765 [hep-ph]
L. Meng, N. Li, S. l. Zhu, arXiv:1707.03598 [hep-ph]
W. Wang, Z. P. Xing, J. Xu, Eur. Phys. J. C 77(11), 800 (2017). https://doi.org/10.1140/epjc/s10052-017-5363-y. arXiv:1707.06570 [hep-ph]
M. Karliner, J. L. Rosner, Phys. Rev. Lett. 119(20), 202001 (2017). https://doi.org/10.1103/PhysRevLett.119.202001. arXiv:1707.07666 [hep-ph]
T. Gutsche, M. A. Ivanov, J. G. Körner, V. E. Lyubovitskij, Phys. Rev. D 96(5), 054013 (2017). https://doi.org/10.1103/PhysRevD.96.054013. arXiv:1708.00703 [hep-ph]
H. S. Li, L. Meng, Z. W. Liu, S. L. Zhu, arXiv:1708.03620 [hep-ph]
Z. H. Guo, Phys. Rev. D 96(7), 074004 (2017). https://doi.org/10.1103/PhysRevD.96.074004. arXiv:1708.04145 [hep-ph]
Q. F. Lü, K. L. Wang, L. Y. Xiao, X. H. Zhong, arXiv:1708.04468 [hep-ph]
L. Y. Xiao, K. L. Wang, Q. f. Lu, X. H. Zhong, S. L. Zhu, Phys. Rev. D 96(9), 094005 (2017). https://doi.org/10.1103/PhysRevD.96.094005. arXiv:1708.04384 [hep-ph]
N. Sharma, R. Dhir, arXiv:1709.08217 [hep-ph]
Y. L. Ma, M. Harada, arXiv:1709.09746 [hep-ph]
L. Meng, H. S. Li, Z. W. Liu, S. L. Zhu, arXiv:1710.08283 [hep-ph]
R. H. Li, C. D. Lü, W. Wang, F. S. Yu, Z. T. Zou, Phys. Lett. B 767, 232 (2017). https://doi.org/10.1016/j.physletb.2017.02.003. arXiv:1701.03284 [hep-ph]
C. Y. Wang, C. Meng, Y. Q. Ma, K. T. Chao, arXiv:1708.04563 [hep-ph]
X. H. Hu, Y. L. Shen, W. Wang, Z. X. Zhao, arXiv:1711.10289 [hep-ph]
M. Gronau, D. Wyler, Phys. Lett. B 265, 172 (1991). https://doi.org/10.1016/0370-2693(91)90034-N
M. Gronau, D. London, Phys. Lett. B 253, 483 (1991). https://doi.org/10.1016/0370-2693(91)91756-L
I. Dunietz, Phys. Lett. B 270, 75 (1991). https://doi.org/10.1016/0370-2693(91)91542-4
D. Atwood, I. Dunietz, A. Soni, Phys. Rev. Lett. 78, 3257 (1997). https://doi.org/10.1103/PhysRevLett.78.3257. arXiv:hep-ph/9612433
D. Atwood, I. Dunietz, A. Soni, Phys. Rev. D 63, 036005 (2001). https://doi.org/10.1103/PhysRevD.63.036005. arXiv:hep-ph/0008090
A. Giri, Y. Grossman, A. Soffer, J. Zupan, Phys. Rev. D 68, 054018 (2003). https://doi.org/10.1103/PhysRevD.68.054018. arXiv:hep-ph/0303187
W. Wang, Phys. Rev. D 85, 051301 (2012). https://doi.org/10.1103/PhysRevD.85.051301. arXiv:1110.5194 [hep-ph]
C. S. Kim, R. H. Li, W. Wang, Phys. Rev. D 88(3), 034003 (2013). https://doi.org/10.1103/PhysRevD.88.034003. arXiv:1305.5320 [hep-ph]
M. J. Savage, M. B. Wise, Phys. Rev. D 39, 3346 (1989) Erratum: [Phys. Rev. D 40, 3127 (1989)]. https://doi.org/10.1103/PhysRevD.39.3346, https://doi.org/10.1103/PhysRevD.40.3127
X. G. He, Y. K. Hsiao, J. Q. Shi, Y. L. Wu, Y. F. Zhou, Phys. Rev. D 64, 034002 (2001). https://doi.org/10.1103/PhysRevD.64.034002. arXiv:hep-ph/0011337
Y. K. Hsiao, C. F. Chang, X. G. He, Phys. Rev. D 93(11), 114002 (2016). https://doi.org/10.1103/PhysRevD.93.114002. arXiv:1512.09223 [hep-ph]
T. Aushev et al., arXiv:1002.5012 [hep-ex]
The preliminary Conceptual Design Report can be found at: http://cepc.ihep.ac.cn/preCDR/main_preCDR.pdf
Acknowledgements
The authors are grateful to Jibo He, Xiao-Hui Hu, Cai-Dian Lü, Fu-Sheng Yu, Zhen-Xing Zhao for useful discussions. W.W. thanks Cai-Dian Lü, and Qiang Zhao for their hospitality when this work is finalized at IHEP, CAS. This work is supported in part by National Natural Science Foundation of China under Grant Nos. 11575110, 11655002, 11735010, Natural Science Foundation of Shanghai under Grant Nos. 15DZ2272100 and 15ZR1423100, Shanghai Key Laboratory for Particle Physics and Cosmology, and by MOE Key Laboratory for Particle Physics, Astrophysics and Cosmology.
Author information
Authors and Affiliations
Corresponding author
Appendix A: Relations between nonleptonic decay widths
Appendix A: Relations between nonleptonic decay widths
1.1 A.1: Doubly charmed baryon decays into a charmed baryon and two light mesons
For decays into an anti-triplet baryon, we have thee relations:
We derive the relations for decays into a sextet baryon:
1.2 A.2: \(\Xi _{cc}\) and \(\Omega _{c}\) decays into a octet baryon , a charmed meson and a light meson
The following relations are derived for decays into an octet baryon:
For a decuplet baryon, we have
1.3 A.3: \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a bottom baryon, \(J/\psi \) and a light meson
Decays into an anti-triplet baryon have the relations:
Decays into a sextet baryon have the relations:
1.4 A.4: \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a bcq, an anti-charmed meson and a light meson
1.5 A.5: \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a bcq and two light mesons
1.6 A.6: \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a bottom sextet, a charmed meson and a light meson
1.7 A.7: \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a bottom baryon, an anti-charmed meson and a light meson
Channels involving an anti-triplet baryon have
while decay modes involving a sextet baryon have
1.8 A.8: \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a bottom baryon and two light mesons
For the anti-triplet baryon, we have
Decays into a sextet heavy baryon have
1.9 A.9: \(\Xi _{bb}\) and \(\Omega _{bb}\) decays into a bottom meson, a light decuplet baryon and a light meson
The relations for decay widths are given as:
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Shi, YJ., Wang, W., Xing, Y. et al. Weak decays of doubly heavy baryons: multi-body decay channels. Eur. Phys. J. C 78, 56 (2018). https://doi.org/10.1140/epjc/s10052-018-5532-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-018-5532-7