Weak decays of doubly heavy baryons: SU(3) analysis

Abstract

Motivated by the recent LHCb observation of doubly charmed baryon $\Xi _{cc}^{++}$ in the $\Lambda _c^+ K^-\pi ^+\pi ^+$ final state, we analyze the weak decays of doubly heavy baryons $\Xi _{cc}$, $\Omega _{cc}$, $\Xi _{bc}$, $\Omega _{bc}$, $\Xi _{bb}$ and $\Omega _{bb}$ under the flavor SU(3) symmetry. The decay amplitudes for various semileptonic and nonleptonic decays are parametrized in terms of a few SU(3) irreducible amplitudes. We find a number of relations or sum rules between decay widths and CP asymmetries, which can be examined in future measurements at experimental facilities like LHC, Belle II and CEPC. Moreover, once a few decay branching fractions have been measured in the future, some of these relations may provide hints for exploration of new decay modes.

1 Introduction

The existence of doubly heavy baryons is predicted in the quark model, but the experimental search for doubly heavy baryons has been a while [1,2,3,4,5,6]. Recently, the LHCb collaboration has observed the doubly charmed baryon $\Xi _{cc}^{++}$ with the mass given as [7]

$$\begin{aligned} m_{\Xi _{cc}^{++}} = (3621.40\pm 0.72\pm 0.27\pm 0.14) \,{\mathrm{MeV}}. \end{aligned}$$

(1)

Without no doubt, this observation will make a great impact on the hadron spectroscopy and it will also trigger more interests in this research field [8, 9]. Moreover after this observation, we also anticipate more experimental investigations of decays of doubly heavy baryons. Thus theoretical studies on weak decays of doubly heavy baryons will be of great importance and are strongly required [10,11,12,13,14,15,16,17,18,19,20,21].

QCD as the fundamental theory for strong interactions shows two distinct facets. At high energy, the interaction strength is weak that allows the use of perturbation theory. At low energy, quarks and gluons are confined into hadrons. The large coupling constant prohibits a direct application of perturbative expansions. For a high-energy process with generic hard scattering, one often uses the factorization to separate the high-energy and low-energy degrees of freedoms. The factorization approach has been widely applied to heavy meson decays [22,23,24,25,26,27,28,29,30], in which the long-distance contributions are parametrized in terms of the low-energy inputs, mostly the light-cone distribution amplitudes. For heavy baryon decays, the factorization analysis is much more involved due to the lack of knowledge on low-energy inputs and the complicated hard-scattering kernels, and see Refs. [31,32,33,34,35,36] for some recent discussions.

Table 1 Quantum numbers for the ground state of doubly heavy baryons. The light quark q corresponds to u, d quark. The $J^P$ denotes the total spin and parity of the baryons. The label $S_{h}^{\pi }$ corresponds to the spin of the heavy quark system

In heavy quark decays, the flavor SU(3) symmetry is an useful tool [37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71]. There are a few advantages to adopt the SU(3) symmetry. First once the branching fractions for a few decay channels have been measured, the flavor SU(3) symmetry offers an opportunity to obtain the knowledge on the related channels. Secondly, the investigation of a few related decay channels can allow one to examine the CKM parameters with the help of SU(3) symmetry. Thirdly, when enough data is available, one may use the data to extract the SU(3) irreducible amplitudes. These amplitudes are expected to calculable in different factorization approaches, and can then be used to examine the factorization schemes themselves. Thus in this paper we will use the flavor SU(3) symmetry and analyze various decays of doubly heavy baryons.

The rest of this paper is organized as follows. In Sect. 2, we will collect the representations for the particle multiplets in the SU(3) symmetry. In Sect. 3, we will analyze the semileptonic decays of the doubly heavy baryons. The nonleptonic decays of doubly charmed baryons, doubly bottom baryons and the baryons with b, c quarks are investigated in Sects. 4, 5 and 6, respectively. The last section contains a brief summary.

2 Particle multiplets

In this section, we will collect the representations for the multiplets of the flavor SU(3) group.

Fig. 1

Anti-triplets (a) and sextets (b) of charmed baryons with one charm quark and two light quarks

Quantum numbers of the doubly heavy baryons are derived from the quark model [72] and are given in Table 1. These baryons can form an SU(3) triplet which are expressed as:

$$\begin{aligned}&T_{cc} = \left( \begin{array}{c} \Xi ^{++}_{cc}(ccu) \\ \Xi ^+_{cc}(ccd) \\ \Omega ^+_{cc}(ccs) \end{array}\right) \,,\;\; T_{bc} = \left( \begin{array}{c} \Xi ^+_{bc}(bcu) \\ \Xi ^0_{bc}(bcd) \\ \Omega ^0_{bc}(bcs) \end{array}\right) \,,\nonumber \\&\quad T_{bb} = \left( \begin{array}{c} \Xi ^0_{bb}(bbu) \\ \Xi ^-_{bb}(bbd) \\ \Omega ^-_{bb}(bbs) \end{array}\right) . \end{aligned}$$

(2)

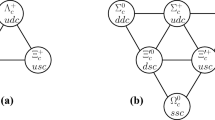
The singly charmed baryons can form an antitriplet or sextet as shown in Fig. 1. In the antitriplet case, we have the matrix expression:

$$\begin{aligned} T_{\mathbf{c}\bar{\mathbf{3}}}= \left( \begin{array}{ccc} 0 &{} \Lambda _c^+ &{} \Xi _c^+ \\ -\Lambda _c^+ &{} 0 &{} \Xi _c^0 \\ -\Xi _c^+ &{} -\Xi _c^0 &{} 0 \end{array} \right) \,. \end{aligned}$$

(3)

For the sextet, we have the multiplet:

$$\begin{aligned} T_{\mathbf{c6}} = \left( \begin{array}{ccc} \Sigma _c^{++} &{} \frac{1}{\sqrt{2}}\Sigma _c^+ &{} \frac{1}{\sqrt{2}} \Xi _c^{\prime +}\\ \frac{1}{\sqrt{2}}\Sigma _c^+&{} \Sigma _c^{0} &{} \frac{1}{\sqrt{2}} \Xi _c^{\prime 0} \\ \frac{1}{\sqrt{2}} \Xi _c^{\prime +} &{} \frac{1}{\sqrt{2}} \Xi _c^{\prime 0} &{} \Omega _c^0 \end{array} \right) \,. \end{aligned}$$

(4)

This is similar for baryons with a bottom quark.

The light baryons form an SU(3) octet and a decuplet. The octet has the expression:

$$\begin{aligned} T_8= \left( \begin{array}{ccc} \frac{1}{\sqrt{2}}\Sigma ^0+\frac{1}{\sqrt{6}}\Lambda ^0 &{} \Sigma ^+ &{} p \\ \Sigma ^- &{} -\frac{1}{\sqrt{2}}\Sigma ^0+\frac{1}{\sqrt{6}}\Lambda ^0 &{} n \\ \Xi ^- &{} \Xi ^0 &{} -\sqrt{\frac{2}{3}}\Lambda ^0 \end{array} \right) , \end{aligned}$$

(5)

while the light baryon decuplet is given as

$$\begin{aligned} (T_{10})^{111}= & {} \Delta ^{++},\;\;\; (T_{10})^{112}= (T_{10})^{121}\nonumber \\= & {} (T_{10})^{211}= \frac{1}{\sqrt{3}} \Delta ^+,\nonumber \\ (T_{10})^{222}= & {} \Delta ^{-},\;\;\; (T_{10})^{122}= (T_{10})^{212}\nonumber \\= & {} (T_{10})^{221}= \frac{1}{\sqrt{3}} \Delta ^0, \nonumber \\ (T_{10})^{113}= & {} (T_{10})^{131}=(T_{10})^{311}= \frac{1}{\sqrt{3}} \Sigma ^{\prime +},\;\;(T_{10})^{223} \nonumber \\= & {} (T_{10})^{232}=(T_{10})^{322}= \frac{1}{\sqrt{3}} \Sigma ^{\prime -},\nonumber \\ (T_{10})^{123}= & {} (T_{10})^{132}=(T_{10})^{213}=(T_{10})^{231}\nonumber \\= & {} (T_{10})^{312}=(T_{10})^{321}= \frac{1}{\sqrt{6}} \Sigma ^{\prime 0},\nonumber \\ (T_{10})^{133}= & {} (T_{10})^{313}=(T_{10})^{331}= \frac{1}{\sqrt{3}} \Xi ^{\prime 0},\;\;(T_{10})^{233} \nonumber \\= & {} (T_{10})^{323}=(T_{10})^{332}= \frac{1}{\sqrt{3}} \Xi ^{\prime -}, \nonumber \\ (T_{10})^{333}= & {} \Omega ^-. \end{aligned}$$

(6)

In the meson sector, the light pseudo-scalar meson is an octet, which can be written as:

$$\begin{aligned} M_{8}=\begin{pmatrix} \frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}} &{}\pi ^+ &{} K^+\\ \pi ^-&{}-\frac{\pi ^0}{\sqrt{2}}+\frac{\eta }{\sqrt{6}}&{}{K^0}\\ K^-&{}\bar{K}^0 &{}-2\frac{\eta }{\sqrt{6}} \end{pmatrix}, \end{aligned}$$

(7)

and we will not consider the flavor singlet $\eta _1$ in this paper. The following analysis is also applicable to the vector meson octet and other light mesons. The charmed meson forms an SU(3) antitriplet:

$$\begin{aligned} D_i=\left( \begin{array}{ccc} D^0,&D^+,&D^+_s \end{array} \right) , \end{aligned}$$

(8)

and the anticharmed meson forms an SU(3) triplet:

$$\begin{aligned} \overline{D}^i=\left( \begin{array}{ccc}\overline{D}^0,&D^-,&D^-_s \end{array} \right) . \end{aligned}$$

(9)

The above two SU(3) triplets are also applicable to the bottom mesons.

3 Semi-leptonic decays

3.1 $\Xi _{cc}$ and $\Omega _{cc}$ decays

The $c\rightarrow q\bar{\ell }\nu$ transition is induced by the effective Hamiltonian:

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} \frac{G_F}{\sqrt{2}} \left[ V_{cq}^* \bar{q} \gamma ^\mu (1-\gamma _5)c \bar{\nu }\gamma _\mu (1-\gamma _5) l\right] +h.c., \end{aligned}$$

(10)

where $q=d,s$ and the $V_{cd}$ and $V_{cs}$ are CKM matrix elements. The heavy-to-light quark operators will form an SU(3) triplet, denoted $H_{ 3}$ with the components $(H_{ 3})^1=0,~(H_{ 3})^2=V_{cd}^*,~(H_{ 3})^3=V_{cs}^*$. At the hadron level, the effective Hamiltonian for decays of $\Xi _{cc}$ and $\Omega _{cc}$ into a singly charmed baryon is constructed as:

$$\begin{aligned}&\mathcal{H}_{\mathrm{eff}}= a_1 (T_{cc})^i (H_{ 3})^j (\overline{T}_{\mathbf{c}\bar{\mathbf{3}}})_{[ij]}~\bar{\nu }_l l\nonumber \\&\quad \qquad +\,a_2 (T_{cc})^i (H_{ 3})^j (\overline{T}_\mathbf{{c 6}})_{\{ij\}} \bar{\nu }_l l\,. \end{aligned}$$

(11)

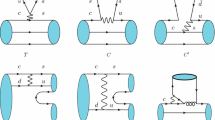
Here the $a_1$ and $a_2$ are SU(3) irreducible nonperturbative amplitudes. The Feynman diagrams for these decays are given in Fig. 2.

The decay amplitudes for different channels can be deduced from the Hamiltonian in Eq. (11), and given in Table 2. From these amplitudes, we can find the relations for decay widths in the SU(3) symmetry limit:

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Lambda _c^+l^+\nu \right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Xi _c^0l^+\nu \right) \nonumber \\= & {} \frac{|V_{cd}|^2}{|V_{cs}|^2}\Gamma (\Xi _{cc}^{++}\rightarrow \Xi _c^+l^+\nu ), \end{aligned}$$

(12)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Xi _c^+l^+\nu \right)= & {} \Gamma \left( \Xi _{cc}^{+}\rightarrow \Xi _c^0l^+\nu \right) , \end{aligned}$$

(13)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}l^+\nu \right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}l^+\nu \right) \nonumber \\= & {} \frac{1}{2}\Gamma \left( \Xi _{cc}^{+}\rightarrow \Sigma _{c}^{0}l^+\nu \right) \nonumber \\= & {} \frac{|V_{cd}|^2}{|V_{cs}|^2} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}l^+\nu \right) , \end{aligned}$$

(14)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}l^+\nu \right)= & {} { }\Gamma \left( \Xi _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}l^+\nu \right) \nonumber \\= & {} \frac{1}{2}\Gamma \left( \Omega _{cc}^{+}\rightarrow \Omega _{c}^{0}l^+\nu \right) . \end{aligned}$$

(15)

Recently, inspired by the LHCb observation of $\Xi _{cc}$, the weak decays of doubly heavy baryons have been studied in Ref. [21], where the authors first derived the hadronic form factors for these transitions in the light-front approach and then applied the results to predict the partial widths for the semi-leptonic and nonleptonic decays of doubly heavy baryons. The SU(3) symmetry can be confronted with these results. We should note that the same comparison in semileptonic $\Xi _{bb}$, $\Omega _{bb}$ and $\Xi _{bc}$, $\Omega _{bc}$ decays and in nonleptonic decays of doubly heavy baryons can also be made. Compared to these explicit model calculations, we found that the SU(3) symmetry works well for the bottom quark decays, while the symmetry breaking effects are sizable for the charm quark decays, largely due to the phase-space differences.

Fig. 2

The Feynman diagrams for the semileptonic decays of $\Xi _{cc}$ and $\Omega _{cc}$

Table 2 SU(3) amplitudes for doubly charmed baryons $\Xi _{cc}$ and $\Omega _{cc}$ decays into a singly charmed baryon

3.2 Semileptonic $\Xi _{bb}$ and $\Omega _{bb}$ decays

The b quark decay is controlled by the Hamiltonian

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} \frac{G_F}{\sqrt{2}} \left[ V_{q'b} \bar{q}' \gamma ^\mu (1-\gamma _5)b \bar{l}\gamma _\mu (1-\gamma _5) \nu \right] +h.c.,\nonumber \\ \end{aligned}$$

(16)

with $q'=u,c$. The $b\rightarrow c$ transition is an SU(3) singlet, while the $b\rightarrow u$ transition forms an SU(3) triplet $H_{3}'$ with $(H_3')^1=1$ and $(H_3')^{2,3}=0$. The Feynman diagrams can be obtained from Fig. 2 by replacing the c quark by b quark, and the final d / s quarks replaced by the c / u quark. The hadron-level Hamiltonian for the semileptonic $\Xi _{bb}$ and $\Omega _{bb}$ decays is constructed as

$$\begin{aligned} H_{\mathrm{eff}}= & {} a_3 (T_{bb})^i (\overline{T}_{bc})_i~\bar{l} \nu _l \,+ a_4 (T_{bb})^i (H_{ 3}')^j (\overline{T}_{\mathbf{b}{\bar{\mathbf{3}}}})_{[ij]}~\bar{l}\nu _l \nonumber \\&+\, a_5 (T_{bb})^i (H_{ 3}')^j (\overline{T}_\mathbf{{b6}})_{\{ij\}}~\bar{l} \nu _l. \end{aligned}$$

(17)

The Feynman diagrams for these decays are given in Fig. 3. The decay amplitudes can be deduced from this Hamiltonian, and the results are given in Table 3. It leads to the relations for the decay widths:

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{bc}^{+}l^-\bar{\nu }\right)= & {} { }\Gamma \left( \Xi _{bb}^{-}\rightarrow \Xi _{bc}^{0}l^-\bar{\nu }\right) \nonumber \\= & {} { }\Gamma \left( \Omega _{bb}^{-}\rightarrow \Omega _{bc}^{0}l^-\bar{\nu }\right) , \end{aligned}$$

(18)

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{-}\rightarrow \Lambda _b^0l^-\bar{\nu }\right)= & {} { }\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _b^0l^-\bar{\nu }\right) , \end{aligned}$$

(19)

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma _{b}^{+}l^-\bar{\nu }\right)= & {} 2\Gamma \left( \Xi _{bb}^{-}\rightarrow \Sigma _{b}^{0}l^-\bar{\nu }\right) \nonumber \\= & {} 2\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime 0}l^-\bar{\nu }\right) . \end{aligned}$$

(20)

Fig. 3

The Feynman diagrams for the semileptonic decays of $\Xi _{bb}$ and $\Omega _{bb}$

Table 3 Similar to Table 2 but for the doubly bottom baryons

Fig. 4

The Feynman diagrams for $\Xi _{cc}$ and $\Omega _{cc}$ decays into a charmed baryon and a light meson

3.3 Semileptonic $\Xi _{bc}$ and $\Omega _{bc}$ decays

The effective Hamiltonian for the semileptonic $\Xi _{bc}$ and $\Omega _{bc}$ decays is given by

$$\begin{aligned} \mathcal{H}_{\mathrm{eff}}= & {} a_6 (T_{bc})^i (\overline{T}_{cc})_i~\bar{l} \nu _l \,+a_7 (T_{bc})^i (H_{ 3}')^j (\overline{T}_{\mathbf{c}\bar{\mathbf{3}}})_{[ij]}~\bar{l}\nu _l \nonumber \\&+ \, a_{8} (T_{bc})^i (H_{ 3}')^j (\overline{T}_\mathbf{{c 6}})_{\{ij\}}~\bar{l}\nu _l \nonumber \\&+ \, a_{9} (T_{bc})^i (H_{ 3})^j (\overline{T}_{\mathbf{b}\bar{\mathbf{3}}})_{[ij]}~\bar{\nu }_l l \nonumber \\&+\, a_{10} (T_{bc})^i ( H_{ 3})^j (\overline{T}_\mathbf{{b6}})_{\{ij\}}~\bar{\nu }_l l. \end{aligned}$$

(21)

In this equation, we have included both charm quark and bottom quark decays. The decay amplitudes for different channels are obtained by expanding the above Hamiltonian and are collected in Table 4.

Table 4 Similar to Table 2 but for the doubly heavy bcq baryons

Apparently, the $\Xi _{bc}$ and $\Omega _{bc}$ decay amplitudes can be obtained by the ones for $T_{cc}$ and $T_{bb}$ decays. For the charm quark decays, one would derive the results with the replacement, $T_{cc}\rightarrow T_{bc}$, $T_c\rightarrow T_b$. The replacement in bottom quark decays is $T_{bb}\rightarrow T_{bc}$, $T_b\rightarrow T_{c}$. Thus we have the following relations for the decay widths:

$$\begin{aligned} \Gamma \left( \Xi _{bc}^{+}\rightarrow \Lambda _b^0 l^+\nu \right)= & {} { }\Gamma \left( \Omega _{bc}^{0}\rightarrow \Xi _b^- l^+\nu \right) \nonumber \\= & {} \frac{|V_{cd}|^2}{|V_{cs}|^2}\Gamma \left( \Xi _{bc}^{+}\rightarrow \Xi _b^0 l^+\nu \right) , \end{aligned}$$

(22)

$$\begin{aligned} \Gamma \left( \Xi _{bc}^{+}\rightarrow \Xi _b^0 l^+\nu \right)= & {} \Gamma \left( \Xi _{bc}^{0}\rightarrow \Xi _b^- l^+\nu \right) , \end{aligned}$$

(23)

$$\begin{aligned} \Gamma \left( \Xi _{bc}^{+}\rightarrow \Sigma _{b}^{0}l^+\nu \right)= & {} { }\Gamma \left( \Omega _{bc}^{0}\rightarrow \Xi _{b}^{\prime -}l^+\nu \right) \nonumber \\= & {} \frac{1}{2}\Gamma \left( \Xi _{bc}^{0}\rightarrow \Sigma _{b}^{-}l^+\nu \right) \nonumber \\= & {} \frac{|V_{cd}|^2}{|V_{cs}|^2}\Gamma \left( \Xi _{bc}^{+}\rightarrow \Xi _{b}^{\prime 0}l^+\nu \right) , \end{aligned}$$

(24)

$$\begin{aligned} \Gamma \left( \Xi _{bc}^{+}\rightarrow \Xi _{b}^{\prime 0}l^+\nu \right)= & {} { }\Gamma \left( \Xi _{bc}^{0}\rightarrow \Xi _{b}^{\prime -}l^+\nu \right) \nonumber \\= & {} \frac{1}{2}\Gamma \left( \Omega _{bc}^{0}\rightarrow \Omega _{b}^{-}l^+\nu \right) , \end{aligned}$$

(25)

$$\begin{aligned} \Gamma \left( \Xi _{bc}^{+}\rightarrow \Xi _{cc}^{++}l^-\bar{\nu }\right)= & {} { }\Gamma \left( \Xi _{bc}^{0}\rightarrow \Xi _{cc}^{+}l^-\bar{\nu }\right) \nonumber \\= & {} { }\Gamma \left( \Omega _{bc}^{0}\rightarrow \Omega _{cc}^{+}l^-\bar{\nu }\right) , \end{aligned}$$

(26)

$$\begin{aligned} \Gamma \left( \Xi _{bc}^{0}\rightarrow \Lambda _c^+l^-\bar{\nu }\right)= & {} { }\Gamma \left( \Omega _{bc}^{0}\rightarrow \Xi _c^+l^-\bar{\nu }\right) , \end{aligned}$$

(27)

$$\begin{aligned} \Gamma \left( \Xi _{bc}^{+}\rightarrow \Sigma _{c}^{++}l^-\bar{\nu }\right)= & {} 2\Gamma \left( \Xi _{bc}^{0}\rightarrow \Sigma _{c}^{+}l^-\bar{\nu }\right) \nonumber \\= & {} 2\Gamma \left( \Omega _{bc}^{0}\rightarrow \Xi _{c}^{\prime +}l^-\bar{\nu }\right) . \end{aligned}$$

(28)

4 Nonleptonic $\Xi _{cc}$ and $\Omega _{cc}$ decays

Usually the charm quark decays into light quarks are categorized into three groups: Cabibbo-allowed, singly Cabibbo-suppressed, and doubly Cabibbo-suppressed:

$$\begin{aligned} c\rightarrow s \bar{d} u, \quad c\rightarrow u \bar{d}d/\bar{s}s, \quad c\rightarrow d \bar{s} u. \end{aligned}$$

(29)

The tree operators transform under the flavor SU(3) symmetry as $\mathbf{3}\otimes {\bar{\mathbf{3}}}\otimes \mathbf{3}=\mathbf{3}\oplus \mathbf{3}\oplus {\bar{\mathbf{6}}}\oplus \mathbf{{15}}$. So the Hamiltonian can be decomposed in terms of a vector $(H_3)$, a traceless tensor antisymmetric in upper indices, $H_\mathbf{\overline{6}}$, and a traceless tensor symmetric in upper indices, $H_\mathbf{{15}}$. As we will show in the following, the vector representation $H_3$ will vanishes as an approximation.

For the $c\rightarrow s u \bar{d}$ transition, we have

$$\begin{aligned} (H_{\overline{6}})^{31}_2=-(H_{\overline{6}})^{13}_2=1, \quad (H_{15})^{31}_2= (H_{15})^{13}_2=1, \end{aligned}$$

(30)

while, for the $c\rightarrow d u \bar{s}$ transition, which is doubly Cabibbo-suppressed, we have

$$\begin{aligned} (H_{\overline{6}})^{21}_3{=}-(H_{\overline{6}})^{12}_3{=}\sin ^2\theta _C, (H_{15})^{21}_3= (H_{15})^{12}_3{=}\sin ^2\theta _C. \nonumber \\ \end{aligned}$$

(31)

For the transition $c\rightarrow u \bar{d}d$, we have

$$\begin{aligned}&(H_{3})^1=1,\;\;\;(H_{\overline{6}})^{21}_2=-(H_{\overline{6}})^{12}_2=(H_{\overline{6}})^{13}_3\nonumber \\&\quad =-(H_{\overline{6}})^{31}_3=\frac{1}{2},\nonumber \\&\frac{1}{3}(H_{15})^{21}_2= \frac{1}{3}(H_{15})^{12}_2\quad =-\frac{1}{2}(H_{15})^{11}_1= -(H_{15})^{13}_3\nonumber \\&=-(H_{15})^{31}_3=\frac{1}{4}, \end{aligned}$$

(32)

with all other remaining entries zero. The overall factor is $V_{cd}^*V_{ud} \simeq -\sin (\theta _C)$. Meanwhile, for the transition $c\rightarrow u \bar{s}s$, we have

$$\begin{aligned}&(H_{3})^1=1,\;\;\;(H_{\overline{6}})^{31}_3=-(H_{\overline{6}})^{13}_3\nonumber \\&\quad =(H_{\overline{6}})^{12}_2=-(H_{\overline{6}})^{21}_2=\frac{1}{2},\nonumber \\&\frac{1}{3}(H_{15})^{31}_3= \frac{1}{3}(H_{15})^{13}_3=-\frac{1}{2}(H_{15})^{11}_1\nonumber \\&\quad = -(H_{15})^{12}_2=-(H_{15})^{21}_2=\frac{1}{4}, \end{aligned}$$

(33)

with all other remaining entries zero. The overall factor is $V_{cs}^*V_{us} \simeq \sin (\theta _C)$. With both the $c\rightarrow u \bar{d}d$ and the $c\rightarrow u \bar{s}s$, the singly Cabibbo-suppressed channel has the following effective Hamiltonian:

$$\begin{aligned}&(H_{\overline{6}})^{31}_3 =-(H_{\overline{6}})^{13}_3 =(H_{\overline{6}})^{12}_2 =-(H_{\overline{6}})^{21}_2 =\sin (\theta _C),\nonumber \\&\quad (H_{15})^{31}_3= (H_{15})^{13}_3=-(H_{15})^{12}_2\nonumber \\&=-(H_{15})^{21}_2= \sin (\theta _C). \end{aligned}$$

(34)

Table 5 Doubly charmed baryons decays into a cqq (antitriplet) and a light meson

Table 6 Doubly charmed baryons decays into a cqq (sextet) and a light meson

4.1 Decays into a charmed baryon and a light meson

With the above expressions, one may derive the effective Hamiltonian for decays involving the antitriplet heavy baryons as

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} b_3(T_{cc})^i (\overline{T}_{c\bar{3}})_{[ij]} M^{k}_{l} (H_{\overline{6}})^{jl}_{k}\nonumber \\&+ \, b_4(T_{cc})^i (\overline{T}_{c\bar{3}})_{[jl]} M^{k}_{i} (H_{\overline{6}})^{jl}_{k}\nonumber \\&+ \, b_5(T_{cc})^i (\overline{T}_{c\bar{3}})_{[jk]} M^{k}_{l} (H_{\overline{6}})^{jl}_{i} \nonumber \\&+ \, b_6(T_{cc})^i (\overline{T}_{c\bar{3}})_{[ij]} M^{k}_{l} (H_{15})^{jl}_{k}\nonumber \\&+ \, b_7(T_{cc})^i (\overline{T}_{c\bar{3}})_{[jk]} M^{k}_{l} (H_{15})^{jl}_{i}. \end{aligned}$$

(35)

For the sextet baryon, we have the Hamiltonian

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} b_{10}(T_{cc})^i (\overline{T}_{c6})_{\{ij\}} M^{k}_{l} (H_{15})^{jl}_{k}\nonumber \\&+ \, b_{11}(T_{cc})^i (\overline{T}_{c6})_{\{jl\}} M^{k}_{i} (H_{15})^{jl}_{k}\nonumber \\&+ \, b_{12}(T_{cc})^i (\overline{T}_{c6})_{\{jk\}} M^{k}_{l} (H_{15})^{jl}_{i} \nonumber \\&+ \, b_{13}(T_{cc})^i (\overline{T}_{c6})_{\{ij\}} M^{k}_{l} (H_{\overline{6}})^{jk}_{l}\nonumber \\&+ \, b_{14}(T_{cc})^i (\overline{T}_{c6})_{\{jk\}} M^{k}_{l} (H_{\overline{6}})^{jl}_{i}. \end{aligned}$$

(36)

The Feynman diagrams for these decays are given in Fig. 4.

Table 7 Doubly charmed baryons decays into a light baryon in the octet and a charmed meson

Expanding the above equations, we will obtain the decay amplitudes given in Table 5 for the antitriplet baryon and Table 6 for the sextet. Thus we have the following relations for decay widths:

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Lambda _c^+\pi ^+ \right)= & {} { }\Gamma \left( \Xi _{cc}^{++}\rightarrow \Xi _c^+K^+ \right) , \end{aligned}$$

(37)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{+}\rightarrow \Xi _c^+K^0 \right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Lambda _c^+\overline{K}^0 \right) , \end{aligned}$$

(38)

$$\begin{aligned} \Gamma \left( \Omega _{cc}^{+}\rightarrow \Xi _c^0\pi ^+ \right)= & {} { }\Gamma \left( \Xi _{cc}^{+}\rightarrow \Xi _c^0K^+ \right) . \end{aligned}$$

(39)

For the decays into the sextet, we have

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Sigma _{c}^{++}\pi ^0 \right)= & {} \frac{1}{3}\Gamma (\Xi _{cc}^{++}\rightarrow \Sigma _{c}^{++}\eta ), \end{aligned}$$

(40)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Sigma _{c}^{+}\pi ^+ \right)= & {} { }\Gamma \left( \Xi _{cc}^{++}\rightarrow \Xi _{c}^{\prime +}K^+ \right) , \end{aligned}$$

(41)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{+}\rightarrow \Sigma _{c}^{++}\pi ^- \right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Sigma _{c}^{++}K^- \right) , \end{aligned}$$

(42)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{+}\rightarrow \Sigma _{c}^{0}\pi ^+ \right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Omega _{c}^{0}K^+ \right) , \end{aligned}$$

(43)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{+}\rightarrow \Xi _{c}^{\prime +}K^0 \right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Sigma _{c}^{+}\overline{K}^0 \right) , \end{aligned}$$

(44)

$$\begin{aligned} \Gamma \left( \Omega _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}\pi ^+ \right)= & {} { }\Gamma \left( \Xi _{cc}^{+}\rightarrow \Xi _{c}^{\prime 0}K^+ \right) . \end{aligned}$$

(45)

Table 8 Doubly charmed baryons decays into a light baryon in the decuplet and a charmed meson

Table 9 Relations for Cabibbo-allowed, singly Cabibbo-suppressed and doubly Cabibbo-suppressed processes in Tables 5 and 7

Table 10 Relations for Cabibbo-allowed, singly Cabibbo-suppressed and doubly Cabibbo-suppressed processes in Table 6

Table 11 Decay width relations for Cabibbo-allowed, singly Cabibbo-suppressed and doubly Cabibbo-suppressed processes in Table 8

Fig. 5

The Feynman diagrams for $\Xi _{cc}$ and $\Omega _{cc}$ decays into a light baryon and a charmed meson

4.2 Decays into a light octet baryon and a charmed meson

The effective Hamiltonian for the decays of $T_{cc}$ into a light octet baryon and a charmed meson is given as

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} c_4(T_{cc})^l \overline{D} ^m \epsilon _{ijk} (T_8)^{k}_{l} (H_{6})^{ij}_m \nonumber \\&+\,c_5(T_{cc})^l \overline{D}^m \epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{ij}_l \nonumber \\&+\,c_6(T_{cc})^l \overline{D} ^i\epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{jm}_l\nonumber \\&+\,c_7(T_{cc})^i \overline{D}^l\epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{jm}_l \nonumber \\&+\,c_8(T_{cc})^l \overline{D}^i\epsilon _{ijk} (T_8)^{k}_{m} (H_{15})^{jm}_l\nonumber \\&+\,c_9(T_{cc})^i \overline{D}^l\epsilon _{ijk} (T_8)^{k}_{m} (H_{15})^{jm}_l. \end{aligned}$$

(46)

In the above Hamiltonian we find the following relations:

$$\begin{aligned} (T_{cc})^l \overline{D} ^m \epsilon _{ijk} (T_8)^{k}_{l} (H_{6})^{ij}_m= -2 (T_{cc})^i \overline{D}^l\epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{jm}_l, \nonumber \\ (T_{cc})^l \overline{D}^m \epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{ij}_l= -2 (T_{cc})^l \overline{D} ^i\epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{jm}_l.\nonumber \\ \end{aligned}$$

(47)

Thus two of the reduced matrix elements are not independent. In the following, we will eliminate the $c_4$ and $c_5$ and use the effective Hamiltonian:

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} c_6(T_{cc})^l \overline{D} ^i\epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{jm}_l\nonumber \\&+\,c_7(T_{cc})^i \overline{D}^l\epsilon _{ijk} (T_8)^{k}_{m} (H_{6})^{jm}_l\nonumber \\&+\,c_8(T_{cc})^l \overline{D}^i\epsilon _{ijk} (T_8)^{k}_{m} (H_{15})^{jm}_l\nonumber \\&+\,c_9(T_{cc})^i \overline{D}^l\epsilon _{ijk} (T_8)^{k}_{m} (H_{15})^{jm}_l. \end{aligned}$$

(48)

The Feynman diagrams for these decays are given in Fig. 5. Expanding the above equations, we will obtain the decay amplitudes given in Table 7, which leads to the relations for decay widths:

$$\begin{aligned}&\Gamma \left( \Xi _{cc}^{++}\rightarrow {p}D^+\right) = { }\Gamma \left( \Xi _{cc}^{++}\rightarrow \Sigma ^+D^+_s\right) ,\;\;\;\nonumber \\&\Gamma \left( \Omega _{cc}^{+}\rightarrow \textstyle \sum ^+ D^0\right) = \Gamma \left( \Xi _{cc}^+\rightarrow p_{}D^0\right) . \end{aligned}$$

(49)

4.3 Decays into a light decuplet baryon and a charmed meson

The effective Hamiltonian for a light decuplet in the final state is given as

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} d_4(T_{cc})^l \overline{D} ^m (T_{10})_{ijl} (H_{15})^{ij}_m \nonumber \\&+\,d_5(T_{cc})^l \overline{D}^m (T_{10})_{ijm} (H_{15})^{ij}_l . \end{aligned}$$

(50)

The Feynman diagrams for these decays are the same as in Fig. 5. The corresponding decay amplitudes are given in Table 8 and it leads to the relations for decay widths:

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{++}\rightarrow \Delta ^{+}D^+\right)= & {} { }\Gamma \left( \Xi _{cc}^{++}\rightarrow \Sigma ^{\prime +}D^+_s\right) , \end{aligned}$$

(51)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{+}\rightarrow \Delta ^{0}D^+\right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Xi ^{\prime 0}D^+_s\right) , \end{aligned}$$

(52)

$$\begin{aligned} \Gamma \left( \Xi _{cc}^{+}\rightarrow \Sigma ^{\prime +}D^0\right)= & {} { }\Gamma \left( \Xi _{cc}^{+}\rightarrow \Xi ^{\prime 0}D^+_s\right) , \end{aligned}$$

(53)

$$\begin{aligned} \Gamma \left( \Omega _{cc}^{+}\rightarrow \Delta ^{+}D^0\right)= & {} { }\Gamma \left( \Omega _{cc}^{+}\rightarrow \Delta ^{0}D^+\right) , \end{aligned}$$

(54)

$$\begin{aligned} \Gamma \left( \Omega _{cc}^{+}\rightarrow \Sigma ^{\prime 0}D^+\right)= & {} { }\Gamma \left( \Xi _{cc}^{+}\rightarrow \Sigma ^{\prime 0}D^+_s\right) .\nonumber \\ \Gamma \left( \Xi _{cc}^{++}\rightarrow \Delta ^{+}D^+_{s}\right)= & {} { }\Gamma \left( \Xi _{cc}^{++}\rightarrow \Delta ^{0}D^+_s\right) ,\nonumber \\ \Gamma \left( \Xi _{cc}^{++}\rightarrow \Sigma ^{\prime +}D^+\right)= & {} { }\Gamma \left( \Omega _{cc}^{++}\rightarrow \Xi ^{\prime 0}D^+\right) ,\nonumber \\ \Gamma \left( \Xi _{cc}^{++}\rightarrow \Delta ^{+}D^{0}\right)= & {} { }\Gamma \left( \Omega _{cc}^{++}\rightarrow \Sigma ^{\prime +}D^0\right) , \end{aligned}$$

(55)

In addition from the decay amplitudes, one can see that there are relations between the widths between Cabibbo-allowed, singly Cabibbo-suppressed and doubly Cabibbo-suppressed decay modes:

$$\begin{aligned} r ^2 = \frac{\Gamma ({\mathrm{channel}} \;\; 1)}{\Gamma ({\mathrm{channel}}\;\; 2)}. \end{aligned}$$

(56)

These relations are given in Tables 9, 10 and 11, respectively.

5 Nonleptonic $\Xi _{bb}$ and $\Omega _{bb}$ decays

For the bottom quark decay, there are generically four kinds of quark-level transitions:

$$\begin{aligned} b\rightarrow c\bar{c} d/s, \; b\rightarrow c \bar{u} d/s, \; b\rightarrow u \bar{c} d/s, \; b\rightarrow q_1 \bar{q}_2 q_3, \end{aligned}$$

(57)

with $q_{1,2,3}$ being the light quarks. Each of them will induce more than one types of decay modes at hadron level, which will be analyzed in order in the following.

Fig. 6

The Feynman diagrams for $\Xi _{bb}$ and $\Omega _{bb}$ decays into $J/\psi$ and a bottom baryon

5.1 $b\rightarrow c\bar{c} d/s$

5.1.1 Decays into $J/\psi$ plus a bottom baryon

Such decays have the same topology as semileptonic $b\rightarrow s\ell ^+\ell ^-$ decays. The transition operator $b\rightarrow c\bar{c}d/s$ can form an SU(3) triplet, leadings to the effective Hamiltonian:

$$\begin{aligned} H_{\mathrm{eff}}= & {} a_1 (T_{bb})^i (H_{ 3})^j (\overline{T}_\mathbf{{b}\overline{3}})_{[ij]}~ J/\psi \nonumber \\&+ \, a_2 (T_{bb})^i (H_{ 3})^j (\overline{T}_\mathbf{{b6}})_{\{ij\}}~J/\psi , \end{aligned}$$

(58)

with $(H_{ 3})_{2}=V_{cd}^*$ and $(H_{ 3})_{3}=V_{cs}^*$. Feynman diagrams for these decays are given in Fig. 6.

The decay amplitudes are given in Table 12. Thus we have the following relations for decay widths:

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Lambda _b^0J/\psi \right)= & {} { }\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _b^-J/\psi \right) , \end{aligned}$$

(59)

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _b^0J/\psi \right)= & {} { }\Gamma \left( \Xi _{bb}^{-}\rightarrow \Xi _b^-J/\psi \right) , \end{aligned}$$

(60)

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma _{b}^{0}J/\psi \right)= & {} { }\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime -}J/\psi \right) \nonumber \\= & {} \frac{1}{2}\Gamma \left( \Xi _{bb}^{-}\rightarrow \Sigma _{b}^{-}J/\psi \right) , \end{aligned}$$

(61)

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{b}^{\prime 0}J/\psi \right)= & {} { }\Gamma \left( \Xi _{bb}^{-}\rightarrow \Xi _{b}^{\prime -}J/\psi \right) \nonumber \\= & {} \frac{1}{2}\Gamma \left( \Omega _{bb}^{-}\rightarrow \Omega _{b}^{-}J/\psi \right) . \end{aligned}$$

(62)

Table 12 Doubly bottom baryons decays into a $J/\psi$ and a light baryon

5.1.2 Decays into a doubly heavy baryon bcq plus a anticharmed meson

The $b\rightarrow c\bar{c}d/s$ transition can lead to another type of effective Hamiltonian:

$$\begin{aligned} H_{\mathrm{eff}}= a_3 (T_{bb})^i (H_{ 3})^j (\overline{T}_{bc})_i D_j+ a_4 (T_{bb})^i (H_{ 3})^j (\overline{T}_{bc})_j D_i,\nonumber \\ \end{aligned}$$

(63)

which corresponds to the decays into doubly heavy baryon bcq plus a anticharmed meson. The Feynman diagrams for these decays are given in Fig. 7. The decay amplitudes are given in Table 13. Thus we obtain the following relations for the decay widths:

$$\begin{aligned}&\Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{bc}^{0}\overline{D}^0\right) = { }\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _{bc}^{0}D^-_s\right) ,\;\;\;\nonumber \\&\quad \Gamma \left( \Xi _{bb}^{0}\rightarrow \Omega _{bc}^{0}\overline{D}^0\right) = { }\Gamma \left( \Xi _{bb}^{-}\rightarrow \Omega _{bc}^{0}D^-\right) .\nonumber \\&\Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{bc}^{+} D^-\right) = { }\Gamma \left( \Omega _{bb}^{-}\rightarrow \Omega _{bc}^{0}D^-\right) ,\;\;\;\nonumber \\&\quad \Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{bc}^{+} D^-_{s}\right) = { }\Gamma \left( \Xi _{bb}^{-}\rightarrow \Xi _{bc}^{0}D^-_{s}\right) . \end{aligned}$$

(64)

Fig. 7

The Feynman diagrams for $\Xi _{bb}$ and $\Omega _{bb}$ decays into a doubly heavy baryon and an anticharmed meson

Table 13 Doubly bottom baryons decays into a bcq and an anticharmed meson

Fig. 8

The Feynman diagrams for $\Xi _{bb}$ and $\Omega _{bb}$ decays into a doubly heavy baryon and a light meson

Table 14 Doubly bottom baryons decays into a bcq and a light meson

5.2 $b\rightarrow c \bar{u} d/s$ transition

5.2.1 Decays into a doubly heavy baryon bcq plus a light meson

The operator to produce a charm quark from the b-quark decay, $\bar{c} b \bar{q} u$, is given by

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} \frac{G_{F}}{\sqrt{2}} V_{cb} V_{uq}^{*} \big [ C_{1} O^{\bar{c}u}_{1} + C_{2} O^{\bar{c}u}_{2}\Big ] +{\mathrm{h.c.}} . \end{aligned}$$

(65)

The light quarks in this effective Hamiltonian form an octet with the non-zero entry

$$\begin{aligned} (H_{\mathbf{8}})^2_1 =V_{ud}^*, \end{aligned}$$

(66)

for the $b\rightarrow c\bar{u}d$ transition, and $(H_{\mathbf{8}})^3_1 =V_{us}^*$ for the $b\rightarrow c\bar{u}s$ transition. The hadron-level effective Hamiltonian is then given as

$$\begin{aligned} \mathcal{H}_{\mathrm{eff}}= & {} a_5 (T_{bb})^i (\overline{T}_{bc})_i M^k_j (H_{\mathbf{8}})^j_k\nonumber \\&+\, a_6 (T_{bb})^i (\overline{T}_{bc})_j M^k_i (H_{\mathbf{8}})^j_k\nonumber \\&+a_7 (T_{bb})^i (\overline{T}_{bc})_k M^k_j (H_{\mathbf{8}})^j_i. \end{aligned}$$

(67)

The Feynman diagrams for these decays are given in Fig. 8. The decay amplitudes are given in Table 14, which leads to:

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Omega _{bc}^{0}\pi ^0 \right) = \frac{1}{2}\Gamma \left( \Xi _{bb}^{-}\rightarrow \Omega _{bc}^{0}\pi ^- \right) . \end{aligned}$$

(68)

5.2.2 Decays into a bottom baryon bqq plus a charmed meson

The effective Hamiltonian from the operator $\bar{c} b \bar{q} u$ gives

$$\begin{aligned} \mathcal{H}_{\mathrm{eff}}= & {} a_8 (T_{bb})^i (\overline{T}_{b\bar{3}})_{[ij]} \overline{D}^k (H_{\mathbf{8}})^j_k\nonumber \\&+\, a_9 (T_{bb})^i (\overline{T}_{b\bar{3}})_{[jk]} \overline{D}^k (H_{\mathbf{8}})^j_i \nonumber \\&+\, a_{10} (T_{bb})^i (\overline{T}_{b6})_{\{ij\}} \overline{D}^k (H_{\mathbf{8}})^j_k\nonumber \\&+ \,a_{11} (T_{bb})^i (\overline{T}_{b6})_{\{jk\}} \overline{D}^k (H_{\mathbf{8}})^j_i. \end{aligned}$$

(69)

The Feynman diagrams for these decays are given in Fig. 9. Results are given in Table 15, thus we have the relations for decay amplitudes:

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma _{b}^{-}D^+\right)= & {} 2\Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{b}^{\prime -}D^+_s\right) ,\;\;\nonumber \\ \Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{b}^{\prime -}D^+\right)= & {} \frac{1}{2}\Gamma \left( \Xi _{bb}^{0}\rightarrow \Omega _{b}^{-}D^+_s\right) .\nonumber \\ \Gamma \left( \Xi _{bb}^{-}\rightarrow \Sigma _{b}^{-}D^0\right)= & {} 2\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime -}D^0\right) ,\nonumber \\ \Gamma \left( \Xi _{bb}^{-}\rightarrow \Xi _{b}^{\prime -}D^0\right)= & {} \frac{1}{2}\Gamma \left( \Omega _{bb}^{-}\rightarrow \Omega _{b}^{-}D^0\right) . \end{aligned}$$

(70)

Fig. 9

The Feynman diagrams for $\Xi _{bb}$ and $\Omega _{bb}$ decays into a bottom baryon and a charmed meson

Table 15 Doubly bottom baryons decays into a bqq and a charmed meson

5.3 $b\rightarrow u \bar{c} d/s$: decays into a bottom baryon bqq plus an anticharmed meson.

For the anticharm production, the operator having the quark contents $(\bar{u}b)(\bar{q}c)$ is given by

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} \frac{G_{F}}{\sqrt{2}} V_{ub} V_{cq}^{*} \big [ C_{1} O^{\bar{u}c}_{1} + C_{2} O^{\bar{u}c}_{2}\Big ]+ {\mathrm{h.c.}}. \end{aligned}$$

(71)

The two light antiquarks form the $\overline{\mathbf {3}}$ and $\mathbf{6}$ representations. The antisymmetric tensor $H_{\bar{3}}''$ and the symmetric tensor $H_{ 6}$ have non-zero components

$$\begin{aligned} \left( H_{\bar{3}}''\right) ^{13} =- \left( H_{\bar{3}}''\right) ^{31} =V_{cs}^*,\;\;\; \left( H_{\bar{6}}\right) ^{13} =\left( H_{\bar{6}}\right) ^{31} =V_{cs}^*,\nonumber \\ \end{aligned}$$

(72)

for the $b\rightarrow u\bar{c}s$ transition. For the transition $b\rightarrow u\bar{c}d$ one requires the interchange of $2\leftrightarrow 3$ in the subscripts, and $V_{cs}$ replaced by $V_{cd}$.

The effective Hamiltonian is constructed as

$$\begin{aligned} \mathcal{H}_{\mathrm{eff}}= & {} b_{1} (T_{bb})^i (\overline{T}_{b\bar{3}})_{[ij]} D_k (H_{\bar{3}}'')^{jk}\nonumber \\&+\,b_{2} (T_{bb})^k (\overline{T}_{b\bar{3}})_{[ij]} D_k (H_{\bar{3}}'')^{ij}\nonumber \\&+\,b_{3} (T_{bb})^i (\overline{T}_{b\bar{3}})_{[ij]} D_k (H_{ 6}'')^{jk} \nonumber \\&+ \, b_{4} (T_{bb})^i (\overline{T}_{b6})_{\{ij\}} D_k (H_{ 6}'')^{jk}\nonumber \\&+\,b_{5} (T_{bb})^k (\overline{T}_{b6})_{\{ij\}} D_k (H_{\bar{6}}'')^{ij}\nonumber \\&+\,b_{6} (T_{bb})^i (\overline{T}_{b6})_{\{ij\}} D_k (H_{\bar{3}}'')^{jk}. \end{aligned}$$

(73)

The Feynman diagrams for these decays are given in Fig. 10. The decay amplitudes for different channels are given in Table 16.

Thus we have the relations for decay amplitudes:

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma _{b}^{+}D^{-}\right)= & {} 2\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime 0}D^{-}\right) ,\nonumber \\ \Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma _{b}^{+} D^{-}_{s}\right)= & {} 2\Gamma \left( \Xi _{bb}^{-}\rightarrow \Sigma _{b}^{0}D^{-}_{s}\right) ,\nonumber \\ \Gamma \left( \Xi _{bb}^{-}\rightarrow \Sigma _{b}^{-}\overline{D}^{0}\right)= & {} 2\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi _{b}^{\prime -}\overline{D}^{0}\right) ,\nonumber \\ \Gamma \left( \Xi _{bb}^{-}\rightarrow \Xi _{b}^{\prime -}\overline{D}^{0}\right)= & {} \frac{1}{2}\Gamma \left( \Omega _{bb}^{-}\rightarrow \Omega _{b}^{-}\overline{D}^{0}\right) . \end{aligned}$$

Fig. 10

The Feynman diagrams for $\Xi _{bb}$ and $\Omega _{bb}$ decays into a bottom baryon and an anticharmed meson

Table 16 Doubly bottom baryons decays into a bqq and an anticharmed meson

As one can see, the $\Xi _{bb}$ can decay into both $\Xi _{b} D^0$ and $\Xi _{b} \overline{D}^0$. The $D^0$ and $\overline{D}^0$ can form the CP eigenstate $D_{+}$ and $D_-$. Thus using the $\Xi _{bb}$ decays into the $\Xi _{b}D_\pm$, one may construct the interference between the $b\rightarrow c\bar{u}s$ and $b\rightarrow u\bar{c}s$. The CKM angle $\gamma$ can then be extracted from measuring decay widths of these channels, as in the case of $B\rightarrow DK$ [73,74,75,76,77,78], $B\rightarrow DK^*_{0,2}$ [79, 80] and others. This is also similar for the $\Omega _{bb}\rightarrow \Omega ^-D_\pm$ decays and the following $\Xi _{bc}\rightarrow \Xi _c D_\pm$ and $\Omega _{bc}\rightarrow \Omega ^0 D_{\pm }$ modes.

5.4 Charmless $b\rightarrow q_1 \bar{q}_2 q_3$ decays

5.4.1 Decays into a bottom baryon and a light meson

The charmless $b\rightarrow q$ ($q=d,s$) transition is controlled by the weak Hamiltonian $\mathcal{H}_\mathrm{{eff}}$:

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} \frac{G_{F}}{\sqrt{2}} \bigg \{ V_{ub} V_{uq}^{*} \big [ C_{1} O^{\bar{u}u}_{1} + C_{2} O^{\bar{u}u}_{2}\Big ]- V_{tb} V_{tq}^{*} \bigg [{\sum \limits _{i=3}^{10}} C_{i} O_{i} \bigg ]\bigg \}+ \text{ h.c. } ,\nonumber \\ \end{aligned}$$

(74)

where $O_{i}$ is a four-quark operator or a moment type operator. At the hadron level, penguin operators behave as the $\mathbf{3}$ representation while tree operators can be decomposed in terms of a vector $H_\mathbf{3}$, a traceless tensor antisymmetric in upper indices, $H_\mathbf{\overline{6}}$, and a traceless tensor symmetric in upper indices, $H_\mathbf{{15}}$. For the $\Delta S=0 (b\rightarrow d)$ decays, the non-zero components of the effective Hamiltonian are [37, 45, 58]

$$\begin{aligned}&(H_3)^2=1,\;\;\;(H_{\overline{6}})^{12}_1=-(H_{\overline{6}})^{21}_1\nonumber \\&\quad =(H_{\overline{6}})^{23}_3=-(H_{\overline{6}})^{32}_3=1,\nonumber \\&2(H_{15})^{12}_1= 2(H_{15})^{21}_1=-3(H_{15})^{22}_2\nonumber \\&\quad = -6(H_{15})^{23}_3=-6(H_{15})^{32}_3=6, \end{aligned}$$

(75)

and all other remaining entries are zero. For the $\Delta S=1(b\rightarrow s)$ decays the non-zero entries in the $H_\mathbf{{3}}$, $H_\mathbf{\overline{6}}$, $H_\mathbf{{15}}$ are obtained from Eq. (75) with the exchange $2\leftrightarrow 3$.

The effective hadron-level Hamiltonian for decays into the bottom antitriplet is constructed as

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} c_1(T_{bb})^i (\overline{T}_{b\bar{3}})_{[ij]} M^{j}_{l} (H_{3})^l \nonumber \\&+c_2(T_{bb})^i (\overline{T}_{b\bar{3}})_{[jl]} M^{j}_{i} (H_{3})^l \nonumber \\&+ \, c_3(T_{bb})^i (\overline{T}_{b\bar{3}})_{[ij]} M^{k}_{l} (H_{\bar{6}})^{jl}_{k}\nonumber \\&+ \, c_4(T_{bb})^i (\overline{T}_{b\bar{3}})_{[jl]} M^{k}_{i} (H_{\bar{6}})^{jl}_{k}\nonumber \\&+ \, c_5(T_{bb})^i (\overline{T}_{b\bar{3}})_{[jk]} M^{k}_{l} (H_{\bar{6}})^{jl}_{i} \nonumber \\&+ \, c_6(T_{bb})^i (\overline{T}_{b\bar{3}})_{[ij]} M^{k}_{l} (H_{15})^{jl}_{k}\nonumber \\&+ \, c_7(T_{bb})^i (\overline{T}_{b\bar{3}})_{[jk]} M^{k}_{l} (H_{15})^{jl}_{i}, \end{aligned}$$

(76)

while, for the sextet baryon, we have

Fig. 11

The Feynman diagrams for $\Xi _{bb}$ and $\Omega _{bb}$ decays into a bottom baryon and a light meson

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} c_8(T_{bb})^i (\overline{T}_{b6})_{\{ij\}} M^{j}_{l} (H_{3})^l \nonumber \\&+c_9(T_{bb})^i (\overline{T}_{b6})_{\{jl\}} M^{j}_{i} (H_{3})^l \nonumber \\&+\, c_{10}(T_{bb})^i (\overline{T}_{b6})_{\{ij\}} M^{k}_{l} (H_{15})^{jl}_{k}\nonumber \\&+ \,c_{11}(T_{bb})^i (\overline{T}_{b6})_{\{jl\}} M^{k}_{i} (H_{15})^{jl}_{k}\nonumber \\&+ \,c_{12}(T_{bb})^i (\overline{T}_{b6})_{\{jk\}} M^{k}_{l} (H_{15})^{jl}_{i} \nonumber \\&+ \, c_{13}(T_{bb})^i (\overline{T}_{b6})_{\{ij\}} M^{k}_{l} (H_{\bar{6}})^{jl}_{k}\nonumber \\&+ \, c_{14}(T_{bb})^i (\overline{T}_{b6})_{\{jk\}} M^{k}_{l} (H_{\bar{6}})^{jl}_{i}. \end{aligned}$$

(77)

The Feynman diagrams for these decays are given in Fig. 11. The decay amplitudes for different channels are given in Tables 17 and 18 for the $b\rightarrow d$ transition and the $b\rightarrow s$ transition, respectively. Thus, it leads to the relations for the decay widths,

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma _{b}^{-}\pi ^+ \right)= & {} 2\Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{b}^{\prime -}K^+ \right) , \end{aligned}$$

(78)

$$\begin{aligned} \Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi _{b}^{\prime -}\pi ^+ \right)= & {} \frac{1}{2}\Gamma \left( \Xi _{bb}^{0}\rightarrow \Omega _{b}^{-}K^+ \right) . \end{aligned}$$

(79)

Table 17 Doubly bottom baryons decays into a bqq and a light meson induced by the charmless $b\rightarrow d$ transition

5.4.2 Decays into a bottom meson and a light baryon octet

The effective Hamiltonian is given as

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} d_1(T_{bb})^i \overline{B} ^j \epsilon _{ijk} (T_8)^{k}_{l} (H_{3})^l \nonumber \\&+ \, d_2(T_{bb})^i \overline{B} ^l \epsilon _{ijk} (T_8)^{k}_{l} (H_{3})^j\nonumber \\&+ \, d_3(T_{bb})^l \overline{B} ^j \epsilon _{ijk} (T_8)^{k}_{l} (H_{3})^i \nonumber \\&+ \, d_4(T_{bb})^l \overline{B} ^n \epsilon _{ijk} (T_8)^{k}_{l} (H_{6})^{ij}_n \nonumber \\&+\, d_5(T_{bb})^l \overline{B} ^n \epsilon _{ijk} (T_8)^{k}_{n} (H_{6})^{ij}_l \nonumber \\&+\, d_6(T_{bb})^l \overline{B} ^i\epsilon _{ijk} (T_8)^{k}_{n} (H_{6})^{jn}_l \nonumber \\&+\,d_7(T_{bb})^i \overline{B}^l\epsilon _{ijk} (T_8)^{k}_{n} (H_{6})^{jn}_l\nonumber \\&+\,d_8(T_{bb})^l \overline{B} ^i\epsilon _{ijk} (T_8)^{k}_{n} (H_{15})^{jn}_l \nonumber \\&+\,d_9(T_{bb})^i \overline{B}^l\epsilon _{ijk} (T_8)^{k}_{n} (H_{15})^{jn}_l. \end{aligned}$$

(80)

Table 18 Doubly bottom baryons decays into a bqq and a light meson induced by the charmless $b\rightarrow s$ transition

Fig. 12

The Feynman diagrams for $\Xi _{bb}$ and $\Omega _{bb}$ decays into a bottom meson and a light baryon

Similarly, we find the reduced matrix elements $d_4,d_7$ and $d_5, d_6$ are not independent. So we use the following effective Hamiltonian:

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} d_1(T_{bb})^i \overline{B} ^j \epsilon _{ijk} (T_8)^{k}_{l} (H_{3})^l \nonumber \\&+ \, d_2(T_{bb})^i \overline{B} ^l \epsilon _{ijk} (T_8)^{k}_{l} (H_{3})^j\nonumber \\&+ \, d_3(T_{bb})^l \overline{B} ^j \epsilon _{ijk} (T_8)^{k}_{l} (H_{3})^i \nonumber \\&+ \, d_6(T_{bb})^l \overline{B} ^i\epsilon _{ijk} (T_8)^{k}_{n} (H_{6})^{jn}_l \nonumber \\&+ \, d_7(T_{bb})^i \overline{B}^l\epsilon _{ijk} (T_8)^{k}_{n} (H_{6})^{jn}_l \nonumber \\&+ \, d_8(T_{bb})^l \overline{B} ^i\epsilon _{ijk} (T_8)^{k}_{n} (H_{15})^{jn}_l \nonumber \\&+ \, d_9(T_{bb})^i \overline{B}^l\epsilon _{ijk} (T_8)^{k}_{n} (H_{15})^{jn}_l. \end{aligned}$$

(81)

The Feynman diagrams for these decays are given in Fig. 12. The decay amplitudes for different channels are given in Tables 19 and 20 for the $b\rightarrow d$ transition and the $b\rightarrow s$ transition, respectively.

5.4.3 Decays into a bottom meson and a light baryon decuplet

The effective Hamiltonian is given as

$$\begin{aligned} \mathcal{H}_\mathrm{{eff}}= & {} f_3(T_{bb})^l \overline{B} ^j (T_{10})_{ijl} (H_{3})^i \nonumber \\&+\, f_4(T_{bb})^l \overline{B} ^n (T_{10})_{ijl} (H_{15})^{ij}_n \nonumber \\&+ \, f_5(T_{bb})^l \overline{B} ^n (T_{10})_{ijn} (H_{15})^{ij}_l. \end{aligned}$$

(82)

The Feynman diagrams for these decays are the same as in Fig. 12. The decay amplitudes for different channels are given in Tables 19 and 20 for the $b\rightarrow d$ transition and the $b\rightarrow s$ transition, respectively.

We summarize the relations for decay widths for $\Xi _{bb}$ and $\Omega _{bb}$ decay into a bottom meson and a light baryon,

$$\begin{aligned}&\Gamma \left( \Xi _{bb}^{0}\rightarrow \Delta ^{0}\overline{B}^0\right) = 2\Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma ^{\prime 0}\overline{B}^0_s\right) , \end{aligned}$$

(83)

$$\begin{aligned}&\Gamma \left( \Xi _{bb}^{-}\rightarrow \Delta ^{-}\overline{B}^0\right) \nonumber \\&\quad = 3\Gamma \left( \Xi _{bb}^{-}\rightarrow \Sigma ^{\prime -}\overline{B}^0_s\right) = 3\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi ^{\prime -}\overline{B}^0_s\right) \nonumber \\&\quad = 3\Gamma \left( \Omega _{bb}^{-}\rightarrow \Sigma ^{\prime -}\overline{B}^0\right) ,\end{aligned}$$

(84)

$$\begin{aligned}&\Gamma \left( \Xi ^{-}_{bb}\rightarrow \Delta ^{0}B^{-}\right) = 2\Gamma \left( \Omega ^{-}_{bb}\rightarrow \Sigma ^{\prime 0}B^{-}\right) .\nonumber \\&\Gamma \left( \Xi ^{-}_{bb}\rightarrow \Delta ^{0}B^{-}\right) = 2\Gamma \left( \Omega ^{-}{bb}\rightarrow \Sigma ^{\prime 0}B^{-}\right) .\nonumber \\&\Gamma \left( \Xi _{bb}^{0}\rightarrow \Sigma ^{\prime 0}\overline{B}^0\right) = \frac{1}{2}\Gamma \left( \Xi _{bb}^{0}\rightarrow \Xi ^{\prime 0}\overline{B}^0_s\right) , \end{aligned}$$

(85)

$$\begin{aligned}&\Gamma \left( \Xi _{bb}^{-}\rightarrow \Sigma ^{\prime -}\overline{B}^0\right) = { }\Gamma \left( \Xi _{bb}^{-}\rightarrow \Xi ^{\prime -}\overline{B}^0_s\right) \nonumber \\&\quad =\Gamma \left( \Omega _{bb}^{-}\rightarrow \Xi ^{\prime -}\overline{B}^0\right) = \frac{1}{3}\Gamma \left( \Omega _{bb}^{-}\rightarrow \Omega ^{-}\overline{B}^0_s\right) .\nonumber \\&\Gamma \left( \Xi ^{-}_{bb}\rightarrow \Xi ^{\prime 0}B^{-}\right) = \frac{1}{2}\Gamma \left( \Omega ^{-}{bb}\rightarrow \Xi ^{\prime 0}B^{-}\right) . \end{aligned}$$

(86)

Table 19 Doubly bottom baryons decays into a bottom meson and a light baryon induced by the charmless $b\rightarrow d$ transition

Table 20 Doubly bottom baryons decays into a bottom meson and a light baryon induced by the charmless $b\rightarrow s$ transitio

5.4.4 U-spin for $\Xi _{bb}$ and $\Omega _{bb}$ decays

For $\Xi _{bb},\Omega _{bb}$ decays induced by the $b\rightarrow q_1q_2q_3$, there are two amplitudes with different CKM factors. We consider the connected decays with the decay amplitudes

$$\begin{aligned} A(\Delta S=0)= & {} r\left( V_{ub}V^*_{ud}A_{\Xi _{bb},\Omega _{bb}}^T+ V_{tb}V_{td}^*A_{\Xi _{bb},\Omega _{bb}}^P \right) , \nonumber \\ A(\Delta S=1)= & {} V_{ub}V^*_{us}A_{\Xi _{bb},\Omega _{bb}}^T+ V_{tb}V_{ts}^*A_{\Xi _{bb},\Omega _{bb}}^P . \end{aligned}$$

(87)

As pointed out in Refs. [40, 43, 44], there exists a relation for the CP violating quantity $\Delta =\Gamma -\bar{\Gamma }$. The relation about decay widths $\Gamma (\Delta S=i)$ and CP asymmetry $A_{CP}(\Delta S=i)$ is

$$\begin{aligned} \frac{A_{CP}(\Delta S=0)}{A_{CP}(\Delta S=1)}= -r^2 \frac{\Gamma (\Delta S=1)}{\Gamma (\Delta S=0)}. \end{aligned}$$

(88)

In Tables 21 and 22, we collect the $\Xi _{bb},\Omega _{bb}$ decay pairs related by U-spin. The CP asymmetries and decay widths for these pairs satisfy relation in Eq. (88). The experimental data in the future is important to test flavor SU(3) symmetry and also the CKM mechanism for CP violation.

Table 21 U-spin relations for $\Xi _{bb},\Omega _{bb}$ decays into a bottom baryon and a light meson. Results in the “channel 1” are for $b\rightarrow d$ processes and the ones in the “channel 2” are for $b\rightarrow s$ processes. r denotes the ratio of the two amplitudes

Table 22 U-spin relations for $\Xi _{bb},\Omega _{bb}$ decays into a bottom meson and a light baryon. Results in the “channel 1” are for $b\rightarrow d$ processes and the ones in the “channel 2” are for $b\rightarrow s$ processes. r denotes the ratio of the two amplitudes

6 Nonleptonic $\Xi _{bc}$ and $\Omega _{bc}$ decays

The decays of $\Xi _{bc}$ and $\Omega _{bc}$ can proceed via the b quark decay or the c quark decay, which are induced by the following quark transitions:

$$\begin{aligned}&c\rightarrow s \bar{d} u, \;\;\; c\rightarrow u \bar{d}d/\bar{s}s, \;\;\; c\rightarrow d \bar{s} u,\nonumber \\&\quad b\rightarrow \bar{c}c d/s, \;\; b\rightarrow c \bar{u}d/s, \;\; b\rightarrow u \bar{c}d/s, \;\; b\rightarrow q_1\bar{q}_2 q_3.\nonumber \\ \end{aligned}$$

(89)

As we have shown in the semileptonic case, for the charm quark decays, one can obtain the decay amplitudes from those for the $\Xi _{cc}$ and $\Omega _{cc}$ decays with the replacement of $T_{cc}\rightarrow T_{bc}$, $T_c\rightarrow T_b$ and $D\rightarrow B$. For the bottom quark decay, one can obtain them from those for $\Xi _{bb}$ and $\Omega _{bb}$ decays with $T_{bb}\rightarrow T_{bc}$, $T_b\rightarrow T_c$ and $B\rightarrow D$. Thus it is not necessary to repeat the tedious calculations here.

7 Conclusions

Quite recently, the LHCb collaboration has observed the doubly charmed baryon $\Xi _{cc}^{++}$ in the final state $\Lambda _c K^-\pi ^+\pi ^+$. Such an important observation will undoubtedly promote the research on the hadron spectroscopy and also on weak decays of doubly heavy baryons.

In this paper, we have analyzed the weak decays of doubly heavy baryons $\Xi _{cc}$, $\Omega _{cc}$, $\Xi _{bc}^{(\prime )}$, $\Omega _{bc}^{(\prime )}$, $\Xi _{bb}$ and $\Omega _{bb}$ under the flavor SU(3) symmetry. The decay amplitudes for various semileptonic and nonleptonic decays have been parametrized in terms of a few SU(3) irreducible amplitudes. We have found a number of relations or sum rules between decay widths and CP asymmetries, which can be examined in future measurements at experimental facilities like LHC, Belle II and CEPC. Moreover, once a few decay branching fractions have been measured in the future, some of these relations may provide hints for the exploration of new decay modes.