1 Introduction

Radiation fluid stars have crucial importance in astrophysics. They can describe the core of neutron stars which is a collection of cold degenerate (non-interacting) fermions [1,2,3,4] and self-gravitating photon stars [4,5,6,7,8]. Such radiative stars, which are called Radiation Pressure Supported Stars (RPSS), are possible even in Newtonian gravity [9] and their relativistic extension, which is called Relativistic Radiation Pressure Supported Stars (RRPSS) [10], can describe the gravitational collapse of massive matter clouds to a very high density fluid. There are also some investigations related with gedanken experiments such as black hole formation and evaporation with self-gravitating gas confined by a spherical symmetric box. These investigations [11, 12] can lead to new insights into the nature of Quantum Gravity.

The radiation fluid stars have the radiative equation of state with \(\rho = 3p \), which is the high density limit of the general isothermal spheres satisfying the linear barotropic equation of state \(\rho = kp \) with constant k. The entropy and thermodynamic stability of self-gravitating charge-less radiation fluid stars were firstly calculated in [5] using Einstein equations. This work was extended to the investigation of structure, stability, and thermodynamic parameters of the isothermal spheres involving photon stars and the core of neutron stars [7, 8]. Also, the numerical study of such a charge-less radiative star which consists of photon gas conglomerations can be found in [6]. Some interesting interior solutions of the general relativistic field equations in isotropic coordinates with the linear barotropic equation of state were presented by Mak and Harko [13,14,15] for dense astrophysical objects without charge.

Furthermore, a spherically symmetric fluid sphere which contains a constant surface charge can be more stable than the charge-less case [16]. The gravitational collapse of a spherically symmetric star may be prevented by charge [17], since the repulsive electric force contributes to counterpoising the gravitational attraction [18]. It is interesting to note that the interior of a strange quark star can be described by a charged solution admitting a one-parameter group of conformal motions [19] for the equation of state \(\rho = 3p + 4B \), which is known as the MIT bag model. The physical properties and structure of the radiation fluid stars in the model with hybrid metric-Palatini gravity [20] and Eddington-inspired Born–Infeld (EIBI) gravity [21] were obtained numerically. It is a challenging problem to find exact interior solutions of the charged radiation fluid stars, since the trace of the gravitational field equations gives a zero Ricci scalar for the radiative equation of state \(\rho =3p\). Therefore it is important to find a modified gravity model which can describe the radiation fluid stars analytically.

In this study we propose a non-minimally coupled modified gravity model in \( Y(R)F^2 \)-form in order to find exact solutions to the radiation fluid stars. Here \(F^2\) is the Maxwell invariant and Y(R) is a function of the Ricci scalar R. We will determine the non-minimal function from physically applicable solutions of the field equations and boundary conditions. Such a coupling in \(RF^2\) form was first introduced by Prasanna [22] to understand the intricate nature between all energy forms, electromagnetic fields, and curvature. Later, a class of such couplings was investigated to gain more insight on charge conservation and curvature [23]. These non-minimal terms can be obtained from the dimensional reduction of a five-dimensional Gauss–Bonnet gravity action [24] and \(R^2\)-type action [25, 26]. The calculation of QED photon propagation in a curved background metric [27] leads to these terms. A generalization of the non-minimal model to \(R^nF^2\)-type couplings [28,29,30,31,32,33] may explain the generation of seed magnetic fields during inflation and the origin of large-scale magnetic fields in the universe [28,29,30]. Another generalization of the non-minimal \(RF^2\) model to non-Riemannian space-times [34] can give more insights into torsion and electromagnetic fields. Then it is possible to consider the more general couplings with any function of the Ricci scalar and the electromagnetic fields such as \(Y(R) F^2\)-form. These non-minimal models in \(Y(R) F^2\)-form have very interesting solutions, such as regular black hole solutions to avoid a singularity [35], spherically symmetric static solutions to explain the rotation curves of galaxies [33, 36,37,38], cosmological solutions to explain cosmic acceleration of the universe [32, 39,40,41], and pp-wave solutions [42].

In order to investigate astrophysical phenomena concerned with charge one can consider Einstein–Maxwell theory, which is a minimal coupling between gravitational and electromagnetic fields. But when the astrophysical phenomena have high density, pressure, and charge such as neutron stars and quark stars, new interaction types between gravitational and electromagnetic fields may appear. Then non-minimally coupled \(Y(R)F^2\) gravity can be ascribed to such new interactions and we can apply the theory to the charged compact stellar system. In this study we focus on exact solutions of the radiation fluid stars for the non-minimally coupled model, inspired by the solution in [19]. We construct the non-minimal coupling function Y(R) with the parameter \(\alpha \) and the corresponding model. We give interior and exterior solutions of the model. Similarly to [19], our interior solutions turn out to be the solution given by Misner and Zapolsky [2] with \(b=0\) and \(Q=0\), describing an ultra high density neutron star or the relativistic Fermi gas. We determine the total mass, charge, and surface gravitational redshift of the stars depending on the boundary radius \(r_b\) and the parameter \(\alpha \) using the matching conditions. We give the general restrictions for the ratios and redshift of the charged compact stars and compare them with the bound given in [43] and the Buchdahl bound [44].

The organization of the present work is as follows: The general action in \(Y(R)F^2\) form and the corresponding field equations are given in Sect. 2 to describe a charged compact star. The spherically symmetric, static exact solutions under conformal symmetry and the structure of the non-minimal function Y(R) are obtained in Sect. 3. Using the continuity and boundary conditions, the gravitational mass, total charge, and redshift of the star are derived in Sect. 4. The conclusions are given in the last section.

2 The model with \(Y(R)F^2 \)-type coupling for a compact star

The recent astronomical observations as regards problems such as dark matter [45, 46] and dark energy [47,48,49,50,51,52] strongly support the idea that Einstein’s theory of gravity needs modification at large scales. Therefore Einstein–Maxwell theory also may be modified [28,29,30, 32, 33, 36,37,38,39,40,41] to explain these observations. Furthermore, since such astrophysical phenomena as neutron stars or quark stars have high energy density, pressure, and electromagnetic fields, new interaction types between gravitational and electromagnetic fields in \(Y(R)F^2\) form might appear. When the extreme conditions are removed, this model turns out to be the minimal Einstein–Maxwell theory. We write the following action to describe the interior of a charged compact star by adding the matter part \(L_\mathrm{mat}\) and the source term \(A\wedge J\) to the \(Y(R)F^2 \)-type non-minimally coupled model in [33, 35,36,37,38,39,40,41]:

$$\begin{aligned} I= & {} \int _M \left\{ \frac{1}{2\kappa ^2} R*1 -Y(R) F\wedge *F + 2A\wedge J \right. \nonumber \\&\left. + L_\mathrm{mat} + \lambda _a\wedge T^a \right\} \end{aligned}$$
(1)

depending on the fundamental variables such that we have the co-frame 1-form \(\{e^a\}\), the connection 1-form \({\{\omega ^a}_b\}\), and the homogeneous electromagnetic field 2-form F. We derive F from the electromagnetic potential 1-form A by \(F=dA\). We constrain the model to the case with zero torsion connection by \(\lambda _a\), a Lagrange multiplier 2-form. Then the variation of \(\lambda _a\) leads to the Levi-Civita connection, which can be found from \(T^a = de^a + \omega ^{a}_{\;\;b} \wedge e^b=0\). In the action (1), J is the electric current density 3-form for the source fluid inside the star, and Y(R) is any function of the curvature scalar R. The scalar can be derived from the curvature tensor 2-forms \( R^{a}_{\;\;b} = d\omega ^{a}_{\;\;b} + \omega ^{a}_{\;\;c} \wedge \omega ^{c}_{\;\;b} \) via the interior product \( \iota _{a}\) such as \( \iota _{b} \iota _{a} R^{ab}= R \). We denote the space-time metric by \(g = \eta _{ab} e^a \otimes e^b\) which has the signature \((-+++)\). Then we set the volume element with \(*1 = e^0 \wedge e^1 \wedge e^2 \wedge e^3 \) on the four dimensional manifold.

For a charged isotropic perfect fluid, electromagnetic and gravitational field equations of the non-minimal model are found from the infinitesimal variations of the action (1)

$$\begin{aligned} d(*Y F)= & {} J \; , \ \end{aligned}$$
(2)
$$\begin{aligned} \ \ dF= & {} 0 \;, \ \end{aligned}$$
(3)
$$\begin{aligned} - \frac{1}{2 \kappa ^2} R_{bc} \wedge *e^{abc}= & {} Y (\iota ^a F \wedge *F - F \wedge \iota ^a *F) \nonumber \\&+ Y_R F_{mn} F^{mn}*R^a \nonumber \\&+ D [ \iota _b\;d(Y_R F_{mn} F^{mn} )]\wedge *e^{ab} \nonumber \\&+ \ (\rho +p )u^a*u + p*e^a, \end{aligned}$$
(4)

where \(Y_R = \frac{\mathrm{{d}}Y}{\mathrm{{d}}R}\) and \(u= u_a e^a \) is the velocity 1-form associated with an inertial time-like observer, \(u_au^a =-1 \). The modified Maxwell equation (2) can be written as

$$\begin{aligned} d*\mathcal {G} = J \end{aligned}$$
(5)

where \(\mathcal {G}=YF\) is the excitation 2-form in the interior medium of the star. A more detailed analysis of this subject can be found in [42, 53, 54]. Following Ref. [40] we write the gravitational field equations (4) as follows:

$$\begin{aligned} G^a = \kappa ^2 \tau ^a_{N} + \kappa ^2 \tau ^a_\mathrm{mat}, \end{aligned}$$
(6)

where \(G^a \) is Einstein tensor \( G^a = - \frac{1}{2 } R_{bc} \wedge *e^{abc} \;, \) \(\tau ^a_{N} \) and \(\tau ^a_\mathrm{mat}\) are two separate effective energy-momentum tensors, namely, the energy-momentum tensor of the non-minimally coupled term introduced in [35, 40] and the energy-momentum tensor of matter, respectively,

$$\begin{aligned} \tau ^a_{N}= & {} Y (\iota ^a F \wedge *F - F \wedge \iota ^a *F) + Y_R F_{mn} F^{mn}*R^a \nonumber \\&+ D [ \iota _b\;d(Y_R F_{mn} F^{mn} )]\wedge *e^{ab}, \end{aligned}$$
(7)
$$\begin{aligned} \tau ^a_\mathrm{mat}= & {} \frac{\delta L_\mathrm{mat}}{\delta e_a } = (\rho +p )u^a*u + p*e^a. \end{aligned}$$
(8)

We take the exterior covariant derivative of the modified gravitational equation (6) in order to show that for the conservation of the total energy-momentum tensor, \(\tau ^a = \tau ^a_{N} + \tau ^a_\mathrm{mat} \),

$$\begin{aligned} DG^a = D\tau ^a. \end{aligned}$$
(9)

The left hand side of Eq. (9) is identically zero, \(DG^a = 0\). The right hand side of Eq. (9) is calculated term by term as follows:

$$\begin{aligned}&D[ Y (\iota ^a F \wedge *F - F \wedge \iota ^a *F)] = 2 J\wedge F^a\nonumber \\&\qquad -\frac{1}{2} F_{mn}F^{mn}\mathrm{{d}}Y \wedge *e^a,\end{aligned}$$
(10)
$$\begin{aligned}&D(Y_RF_{mn}F^{mn} *R^a) = d(Y_RF_{mn}F^{mn}) \wedge *R^a \nonumber \\&\qquad + \frac{1}{2}F_{mn}F^{mn} Y_R \mathrm{{d}}R\wedge *e^a ,\end{aligned}$$
(11)
$$\begin{aligned}&D\left[ D[ \iota _b d(Y_R F_{mn} F^{mn} )]\wedge *e^{ab} \right] \nonumber \\&\quad = D^2 [ \iota _b d(Y_R F_{mn} F^{mn} )]\wedge *e^{ab} ,\end{aligned}$$
(12)
$$\begin{aligned}&\quad = {R_b}^c\wedge \imath _c\;d(Y_R F_{mn} F^{mn} ) *e^{ab} ,\end{aligned}$$
(13)
$$\begin{aligned}&\quad = -d(Y_R F_{mn} F^{mn} )\wedge *R^a\;. \end{aligned}$$
(14)

If we substitute all the expressions in (9) we find

$$\begin{aligned} 0 = D\tau ^a = 2J\wedge F^a + D\tau ^a_\mathrm{mat}, \end{aligned}$$
(15)

which leads to

$$\begin{aligned} D\tau ^a_\mathrm{mat} =-2J\wedge F^a, \end{aligned}$$
(16)

which is similar to the minimally coupled Einstein–Maxwell theory, but where \(J = d(*YF)\) from (2). Then in this case without source, \(J=0\), the conservation of the energy-momentum tensor becomes \( D\tau ^a = 0 = D\tau ^a_\mathrm{mat}.\)

The isotropic matter has the following energy density and pressure: \( \rho = \tau _\mathrm{mat}^{0,0} \), \( p= \tau _\mathrm{mat}^{1,1} = \tau _\mathrm{mat}^{ 2,2} = \tau _\mathrm{mat}^{3,3} \) as the diagonal components of the matter energy-momentum tensor \(\tau ^a_\mathrm{mat}\) in the interior of the star. In order to get over higher order derivatives and the complexity of the last term in (7) we take the following constraint:

$$\begin{aligned} Y_R F_{mn} F^{mn} = \frac{K}{ \kappa ^2} \end{aligned}$$
(17)

where K is a non-zero constant. If one take K is zero, then the non-minimal function Y becomes a constant and this is not different from the well known minimally coupled Einstein–Maxwell theory. The constraint (17) has the following features: First of all, this constraint (17) is not an independent equation from the field equations, since the exterior covariant derivative of the gravitational field equations under the condition gives the constraint again in addition to the conservation equation. Secondly, the field equations (2)–(4) under the condition (17) with \(K=-1\) can be interpreted [40] as the field equations of the trace-free Einstein gravity [55, 56] or unimodular gravity [57, 58] coupled to the electromagnetic energy-momentum tensor with the non-minimal function Y(R), which are viable for astrophysical and cosmological applications. Thirdly, the constraint allows us to find the other physically interesting solutions of the non-minimal model [32, 33, 35, 36, 38, 40, 41]. Fourthly, when we take the trace of the gravitational field equation (4) as done in Ref. [40], we obtain

$$\begin{aligned} \frac{K+1}{\kappa ^2} R*1 = (\rho - 3p)*1. \end{aligned}$$
(18)

We can consider two cases satisfying (18) for the non-minimal \(Y(R)F^2\) coupled model:

  1. 1.

    \(K=-1\), which leads to the equation of state \(\rho = 3 p\) for the radiation fluid stars.

  2. 2.

    \(K\ne - 1 \) with the equation \(R = \frac{\kappa ^2 ( \rho - 3p)}{K+1}\).

Then we set \(K= -1\) in (17) and (18), since we concentrate on the radiation fluid star for the non-minimal model. Therefore we see that the trace of the gravitational field equations does not give a new independent equation as another feature of the condition (17) with \(K=-1\). One may refer to Ref. [40] for a detailed discussion of the physical properties and features of \(\tau _{N}^{a}\) for the case \(K=-1\). We leave the second case with \(K\ne - 1 \), \(\rho \ne 3p\) for next studies. We also note that the non-minimally coupled \(Y(R)F^2\) model does not give any new solution for the MIT bag model \(\rho -3p = 4B\) with \(B \ne 0\), since the curvature scalar R becomes a constant in (18) therewith Y(R) must be constant. Thus this case is not a new model but the minimal Einstein–Maxwell case.

3 Static, spherically symmetric, charged solutions

We seek solutions to the model with \(Y(R)F^2\)-type coupling describing a radiative compact star for the following most general (1+3)-dimensional spherically symmetric, static metric:

$$\begin{aligned} \mathrm{{d}}s^2 = -f^2(r)\mathrm{{d}}t^2 + g^2(r)\mathrm{{d}}r^2 + r^2\mathrm{{d}}\theta ^2 +r^2\sin (\theta )^2 \mathrm{{d}} \phi ^2 \end{aligned}$$
(19)

and the following electromagnetic tensor 2-form with the electric field component E(r):

$$\begin{aligned} F = E(r) e^1\wedge e^0 . \end{aligned}$$
(20)

We take the electric current density as a source of the field which has only the electric charge density component \(\rho _e(r)\),

$$\begin{aligned} J = {\rho } _e(r) e^{1}\wedge e^{2} \wedge e^{3} = {\rho } _e g r^2 \sin \theta \mathrm{{d}}r \wedge \mathrm{{d}}\theta \wedge \mathrm{{d}}\phi . \end{aligned}$$
(21)

Using the Stokes theorem, the integral form of the Maxwell equation (2) can be written as

$$\begin{aligned} \int _{V} d*YF = \int _{\partial V} *YF = \int _V J =4\pi q(r) \end{aligned}$$
(22)

over the sphere which has the volume V and the boundary \(\partial V\). When we take the integral, we find the charge inside the volume with the radius r,

$$\begin{aligned} YEr^2 = q(r) = \int \limits _{0}^{r} {\rho } _e(x) g(x) x^2 \mathrm{{d}}x. \end{aligned}$$
(23)

In (23), the second equality says that the electric charge can also be obtained from the charge density \(\rho _e(r)\) of the star. Then the gravitational field equations (4) lead to the following differential equations for the metric (19) and electromagnetic field (20) of the radiation fluid star \(\rho = 3 p\):

$$\begin{aligned}&\frac{1}{\kappa ^2 g^2}\left( \frac{f''}{f} -\frac{f'g'}{fg} + \frac{2f'}{rf} + \frac{2g'}{rg} + \frac{g^2-1}{r^2} \right) \nonumber \\&\quad = YE^2 + \rho , \end{aligned}$$
(24)
$$\begin{aligned}&\frac{1}{\kappa ^2 g^2}\left( \frac{f''}{f} -\frac{f'g'}{fg} - \frac{2f'}{rf} - \frac{2g'}{rg} + \frac{g^2-1}{r^2} \right) \nonumber \\&\quad = YE^2 - \rho /3, \end{aligned}$$
(25)
$$\begin{aligned}&\frac{1}{ \kappa ^2 g^2}\left( \frac{f''}{f} - \frac{f'g'}{fg} + \frac{g^2 -1 }{r^2} \right) \nonumber \\&\quad = Y E^2 + \rho /3, \end{aligned}$$
(26)

and we have the following conservation relation from the covariant exterior derivative of the gravitational field equations (16):

$$\begin{aligned} p' + 4 p\frac{f'}{f} = 2(YE)'E + \frac{4YE^2}{r} , \end{aligned}$$
(27)

together with the constraint from (17)

$$\begin{aligned} \frac{\mathrm{{d}}Y}{\mathrm{{d}}R} = \frac{1}{ 2\kappa ^2 E^2} \end{aligned}$$
(28)

where the curvature scalar is

$$\begin{aligned} R = \frac{2}{g^2} \left( - \frac{f''}{f} + \frac{f' g' }{fg} - \frac{2f'}{fr} + \frac{2g'}{gr} + \frac{g^2 -1 }{r^2} \right) . \end{aligned}$$
(29)

3.1 Exact solutions under conformal symmetry

We assume that the existence of a one-parameter group of conformal motions for the metric (19)

$$\begin{aligned} L_\xi g_{ab} = \phi (r) g_{ab} \end{aligned}$$
(30)

where \( L_\xi g_{ab}\) is the Lie derivative of the interior metric with respect to the vector field \(\xi \) and \(\phi (r)\) is an arbitrary function of r. The interior gravitational field of stars can be described by using this symmetry [19, 59,60,61]. The metric functions \(f^2(r) \) and \(g^2(r)\) satisfying this symmetry were obtained:

$$\begin{aligned} f^2(r)= & {} a^2 r^2, \quad g^2(r) = \frac{\phi ^2_0}{\phi ^2} \end{aligned}$$
(31)

in [59] where a and \( \phi _0 \) are integration constants. Introducing a new variable \(X = \frac{\phi ^2}{\phi _0^2}\) in (31) and using this symmetry, Eqs. (24)–(28) turn out to be the three differential equations

$$\begin{aligned} -\frac{X'}{\kappa ^2 r} + \frac{2X +2}{\kappa ^2 r^2} - 2\rho= & {} 2 YE^2\;, \end{aligned}$$
(32)
$$\begin{aligned} \frac{X'}{\kappa ^2 r} - \frac{2X}{\kappa ^2 r^2} +\frac{2\rho }{3}= & {} 0 \;,\end{aligned}$$
(33)
$$\begin{aligned} p' + \frac{4p}{r} - 2(YE)'E - \frac{4YE^2}{r}= & {} 0\;. \end{aligned}$$
(34)

Here we note that the constraint (28) is not an independent equation from (32) and (33), since we find the constraint eliminating \(\rho \) from (32)–(33) and taking the derivative of the resulting equation as in [35] (where \( \rho =3p\)). Thus, we have three differential equations (32)–(34) and four unknowns (\(X, \rho , Y, E\)). So a given theory or a non-minimal coupling function Y(R), it may be possible to find the corresponding exact solutions for the functions X, E, and \(\rho \), or inversely, for a convenient choice of any one of the functions X, E, and \(\rho \), we may find the corresponding non-minimal theory via the non-minimal function Y(R). In this paper we will continue with the second case, offering physically acceptable metric solutions. In the second case, one of the challenging problems is to solve r from R(r) and re-express the function Y depending on R.

When we choose the metric function \(g^2(r) = \frac{1}{X } =\frac{3}{ 1 - br^2}\) as a result in [19] with a constant b, we find the constant curvature scalar \(R =4b \) and a constant non-minimal function Y(R). Then this model (1) turns out to be the minimal Einstein–Maxwell case. Therefore we need the non-constant curvature scalar to obtain non-trivial solutions of the non-minimal theory. Inspired by [19], for \(\alpha > 2\) real numbers and \(b\ne 0\), we offer the following metric function:

$$\begin{aligned} g^2(r) = \frac{1}{X} = \frac{3}{ 1 + br^\alpha }, \end{aligned}$$
(35)

which is regular at the origin, \(r=0\), giving the following non-constant and regular curvature scalar:

$$\begin{aligned} R= - b(\alpha +2) r^{\alpha -2}. \end{aligned}$$
(36)

We note that if \(b=0\) the curvature scalar R becomes zero and Y is a constant again. Therefore, here we consider the case with \(b\ne 0\) and obtain the following solutions to Eqs. (32)–(35):

$$\begin{aligned} \rho (r)= & {} \frac{2- br^\alpha (\alpha -2)}{2\kappa ^2 r^2} , \end{aligned}$$
(37)
$$\begin{aligned} Y(r)= & {} c \left[ 1 + b(\alpha -2)r^\alpha \right] ^{-\frac{3(\alpha +2)}{2\alpha }}, \end{aligned}$$
(38)
$$\begin{aligned} E^2(r)= & {} \frac{ \left[ 1 + b(\alpha -2)r^\alpha \right] ^{ \frac{5\alpha +6}{2\alpha } }}{3c \kappa ^2 r^2} . \end{aligned}$$
(39)

Here c is a non-zero integration constant and it will be determined by the exterior Einstein–Maxwell Lagrangian (48) as \(c=1\). Using the charge–radius relation (23), we calculate the total charge inside the volume with radius r,

$$\begin{aligned} q^2(r) =( YEr^2)^2 = \frac{c r^2 \left[ 1+b(\alpha -2)r^\alpha \right] ^{-\frac{\alpha +6}{2\alpha } }}{3\kappa ^2} \;. \end{aligned}$$
(40)

We see that the charge is regular at the origin \(r=0\) for the theory with \(\alpha >2\). Obtaining by the inverse of R(r) from (36)

$$\begin{aligned} r= \left( \frac{-R}{\alpha b + 2b} \right) ^{1/(\alpha -2)} \end{aligned}$$
(41)

the non-minimal coupling function is calculated as

$$\begin{aligned} Y(R)= c \left[ 1 + b(\alpha -2) \left( \frac{-R}{\alpha b +2b} \right) ^{\frac{\alpha }{\alpha -2}} \right] ^{-\frac{3\alpha +6}{2\alpha } }. \end{aligned}$$
(42)

The non-minimal function (42) turns into \(Y(R) = c\) for the vacuum case \(R=0\) and we can choose \(c=1\) to obtain the well-known minimal Einstein–Maxwell theory at the exterior region. Thus the Lagrangian of our non-minimal gravitational theory (1)

$$\begin{aligned} L= & {} \frac{1}{2\kappa ^2} R*1\nonumber \\&- \left[ 1+ b(\alpha -2) \left( \frac{-R}{\alpha b +2b} \right) ^{\frac{\alpha }{\alpha -2} } \right] ^{\frac{-3(\alpha +2)}{2\alpha }} F\wedge *F \nonumber \\&+ 2A\wedge J + L_{mat} + \lambda _a\wedge T^a \ \ \ \ \ \ \end{aligned}$$
(43)

admits the following metric:

$$\begin{aligned} \mathrm{{d}}s^2 = - a^2r^2\mathrm{{d}}t^2 + \frac{3}{1+br^\alpha } \mathrm{{d}}r^2 + r^2(\mathrm{{d}}\theta ^2 +sin^2\theta \mathrm{{d}}\phi ^2 ),\nonumber \\ \end{aligned}$$
(44)

together with the energy density, electric field, and electric charge,

$$\begin{aligned} \rho (r)= & {} \frac{2- br^\alpha (\alpha -2)}{2\kappa ^2 r^2} , \end{aligned}$$
(45)
$$\begin{aligned} E^2(r)= & {} \frac{ \left[ 1 + b(\alpha -2)r^\alpha \right] ^{ \frac{5\alpha +6}{2\alpha } }}{3 \kappa ^2 r^2} ,\end{aligned}$$
(46)
$$\begin{aligned} q^2(r)= & {} \frac{ r^2 \left[ 1+b(\alpha -2)r^\alpha \right] ^{-\frac{\alpha +6}{2\alpha } }}{3\kappa ^2} \; \end{aligned}$$
(47)

under the conformal symmetry (30) describing the interior of the radiation fluid star with \(\alpha >2\). The parameter b in the model will be determined by the matching condition (62) and the parameter \(\alpha \) can be determined by the related observations.

On the other hand, since the exterior region does not have any matter and source the above non-minimal Lagrangian (43) turns into the following sourceless minimal Einstein–Maxwell Lagrangian:

$$\begin{aligned} L = \frac{1}{2\kappa ^2} R*1 - F\wedge *F + \lambda _a\wedge T^a, \end{aligned}$$
(48)

which is the vacuum case with \(Y(R)=1\), and the field equations of the non-minimal theory (2)–(4) turn into the following Einstein–Maxwell field equations due to \(Y_R=0\):

$$\begin{aligned}&d* F = 0 \; , \ \ \ \ dF= 0 \;, \ \end{aligned}$$
(49)
$$\begin{aligned}&- \frac{1}{2 \kappa ^2} R_{bc} \wedge *e^{abc} = \iota ^a F \wedge *F - F \wedge \iota ^a *F, \end{aligned}$$
(50)

which lead to \(R=0\) by the trace equation and admit the following Reissner–Nordstrom metric:

$$\begin{aligned} \mathrm{{d}}s^2= & {} -\left( 1-\frac{2M}{r} + \frac{\kappa ^2Q^2}{r^2}\right) \mathrm{{d}}t^2 \nonumber \\&+ \left( 1-\frac{2M}{r} + \frac{\kappa ^2Q^2}{r^2}\right) ^{-1}\mathrm{{d}}r^2 \nonumber \\&+ r^2(\mathrm{{d}}\theta ^2 +sin^2\theta \mathrm{{d}}\phi ^2 ) \end{aligned}$$
(51)

with the electric field

$$\begin{aligned} E(r) = \frac{Q}{ r^2} \end{aligned}$$
(52)

at the exterior region. Here M is the total gravitational mass and \(Q=q(r_b)\) is the total charge of the star. Since the Ricci scalar is zero for the Reissner–Nordstrom solution, the non-minimal function (42) becomes \(Y=1\) consistent with the above considerations. As we see from (49) the excitation 2-form \(\mathcal {G}= YF\) is replaced by the Maxwell tensor F at the exterior vacuum region. In order to see a concrete example of this non-minimally coupled theory we look at the simplest case where \(\alpha =3\), then the non-minimal Lagrangian is

$$\begin{aligned} L= & {} \frac{1}{2\kappa ^2} R*1 - \left( 1 - \frac{R^3}{5^3b^2} \right) ^{-\frac{5}{2} } F\wedge *F\nonumber \\&+ 2A\wedge J + L_\mathrm{mat} + \lambda _a\wedge T^a \end{aligned}$$
(53)

and its corresponding field equations admit the following interior metric:

$$\begin{aligned} \mathrm{{d}}s^2 = - a^2r^2\mathrm{{d}}t^2 + \frac{3}{1+br^3} \mathrm{{d}}r^2 + r^2(\mathrm{{d}}\theta ^2 +sin^2\theta \mathrm{{d}}\phi ^2 ).\nonumber \\ \end{aligned}$$
(54)

Using the curvature scalar \( R = - 5b r \), we find the energy density, electric field, and charge to be

$$\begin{aligned} \rho (r)= & {} \frac{1}{\kappa ^2 r^2} - \frac{b}{2\kappa ^2}r ,\end{aligned}$$
(55)
$$\begin{aligned} E^2(r)= & {} \frac{(1 + br^3 )^{ \frac{7}{2}}}{3 \kappa ^2 r^2}, \end{aligned}$$
(56)
$$\begin{aligned} q(r)= & {} \frac{r^2(1+br^3)^{-3/2}}{3\kappa ^2}. \end{aligned}$$
(57)

For the exterior region (\(R=0\)), the model (53) turns into the well-known Einstein–Maxwell theory, which admits the above Reissner–Nordstrom solution.

4 Matching conditions

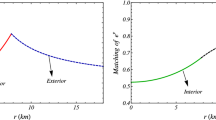
We will match the interior and exterior metric (44), (51) at the boundary of the star \(r=r_b\) for continuity of the gravitational potential,

$$\begin{aligned} a^2r_b^2= & {} 1-\frac{2M}{r_b} + \frac{\kappa ^2 Q^2}{r_b^2}, \end{aligned}$$
(58)
$$\begin{aligned} \frac{3}{1 + br_b^\alpha }= & {} \left( 1-\frac{2M}{r_b} + \frac{\kappa ^2 Q^2}{ r_b^2} \right) ^{-1} . \end{aligned}$$
(59)

The matching conditions (58) and (59) give

$$\begin{aligned} a^2 = \frac{\kappa ^2 Q^2 - 2Mr_b + rb^2 }{r_b^4}\;,\end{aligned}$$
(60)
$$\begin{aligned} b =\frac{ 2r_b^2 - 6Mr_b + 3\kappa ^2Q^2 }{r_b^{2+\alpha }}\;. \end{aligned}$$
(61)

The vanishing pressure condition at the boundary \(r_b\) requires that

$$\begin{aligned} p(r_b) = \frac{2- b(\alpha -2)r_b^\alpha }{6\kappa ^2 r_b^2} = 0, \end{aligned}$$
(62)

and it determines the constant b in the non-minimal model (43) as

$$\begin{aligned} b = \frac{2}{(\alpha -2)r_b^\alpha } \;. \end{aligned}$$
(63)

The interior region of the star can be considered as a specific medium and the exterior region as a vacuum. Then the excitation 2-form \(\mathcal {G}=YF \) in the interior turns into the Maxwell tensor F at the exterior, because of \(Y=1\) in this vacuum region. That is, we use the continuity of the tensor at the boundary which leads to the continuity of the total charge in which a volume V. Then the total charge for the exterior region is obtained from the Maxwell equation (49), \(d*F=0\), taking the integral \(\frac{1}{4\pi }\int _{\partial V} *F= Er^2= Q\), while the total charge in the interior region is given by (23). Thus the total charge Q is determined by setting \(r=r_b\) in (47) as a last matching condition

$$\begin{aligned} q^2(r_b) = \frac{ r_b^2 \left[ 1+b(\alpha -2)r_b^\alpha \right] ^{-\frac{\alpha +6}{2\alpha } }}{3\kappa ^2}= & {} Q^2 \;. \end{aligned}$$
(64)

Substituting (63) in (64) we obtain the following total charge–boundary radius relation:

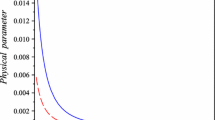
$$\begin{aligned} Q^2= & {} \frac{ r_b^2 }{ \kappa ^2 3^{\frac{3\alpha +6}{2\alpha } }}. \end{aligned}$$
(65)

The ratio \(\frac{\kappa ^2Q^2}{r_b^2}=3^{-\frac{3\alpha +6}{2\alpha } }\), which is obtained from (65) is plotted in Fig. 1 depending on the parameter \(\alpha \) of the model for different \(\alpha \) intervals. As we see from (65) the charge–radius ratio has the upper limit

$$\begin{aligned} \frac{\kappa ^2 Q^2}{r_b^2} = \frac{1}{3\sqrt{3}} \approx 0.1924. \end{aligned}$$
(66)
Fig. 1
figure 1

The square of the charge–radius ratio versus the parameter \(\alpha \)

Full size image

When we compare (63) with (61), we find the following mass–charge relation for the model with the non-minimally coupled electromagnetic fields to gravity:

$$\begin{aligned} M= \left( \frac{\alpha -3}{\alpha -2}\right) \frac{r_b}{3} + \frac{\kappa ^2 Q^2}{2r_b} \; . \end{aligned}$$
(67)

Substituting the total charge (65) in (67) we find the total mass of the star depending on the boundary radius \(r_b\) and the parameter \(\alpha \) of the model

$$\begin{aligned} M= \left( \frac{\alpha -3}{\alpha -2}\right) \frac{r_b}{3} + 3^{-\frac{3\alpha +6}{2\alpha } }\; \frac{r_b}{2}. \end{aligned}$$
(68)

This mass–radius relation is shown in Fig. 2 for two different \(\alpha \) intervals. Taking the limit \(\alpha \rightarrow \infty \;\), we can find the upper bound for the mass–radius ratio,

$$\begin{aligned} \frac{M}{r_b} < \frac{1}{3} + \frac{1 }{6\sqrt{3}} \approx 0.4295, \end{aligned}$$
(69)

which is slightly smaller than the Buchdahl bound [44] and the bound given in [43] for general relativistic charged objects.

Fig. 2
figure 2

The gravitational mass–radius ratio versus the parameter \(\alpha \)

Full size image

Also, the matter mass component of the radiation fluid star is obtained from the following integral of the energy density \(\rho \):

$$\begin{aligned} M_m = \frac{\kappa ^2}{2} \int _0^{r_b} \rho r^2 \mathrm{{d}}r = \frac{\alpha }{2(\alpha +1)} r_b. \end{aligned}$$
(70)

The upper bound of the matter mass for the radiative star is found as \( M_m = \frac{r_b}{2} \; \) taking by the limit \( \alpha \rightarrow \infty \). The dependence of the matter mass–radius ratio on the parameter \(\alpha \) can be seen in Fig. 3.

Fig. 3
figure 3

The matter mass–radius ratio versus the parameter \(\alpha \)

Full size image

Here we emphasize that each different value of \(\alpha \) corresponds to a different non-minimally coupled theory in (43) and each different theory gives a different mass–radius relation.

Fig. 4
figure 4

The gravitational surface redshift versus the parameter \(\alpha \)

Full size image

Additionally, the gravitational surface redshift z is calculated from

$$\begin{aligned} z= \left( 1-\frac{2M}{r_b} + \frac{\kappa ^2 Q^2}{r_b^2}\right) ^{- \frac{1}{2}} -1 = \sqrt{\frac{3(\alpha -2)}{\alpha } } -1. \end{aligned}$$
(71)

Taking the limit \(\alpha \rightarrow \infty \), the inequality for the redshift is found as \(z < \sqrt{3} -1 \approx 0.732\), which is smaller than the bound given in [43] and the Buchdahl bound \(z \le 2\). We plot the redshift depends on the \(\alpha \) in Fig. 4.

For the case \(\alpha =3\), we calculate all the parameters as \(M= \frac{\sqrt{3} r_b}{54}\approx 0.032 r_b \), \( M_m = \frac{3r_b}{8}=0.375r_b\), \( Q^2=\frac{\sqrt{3} r_b^2 }{ 27 \kappa ^2} \approx \frac{0.064r_b^2 }{\kappa ^2} \) from (68), (70), (65). In this case, because of \(\frac{2M}{r_b} = \frac{\kappa ^2 Q^2}{r_b^2}\) at the boundary, the metric functions are equal to 1, \(f(r_b) = g(r_b) = 1 \). This means that the total gravitational mass M together with the energy of the electromagnetic field inside the boundary is exactly balanced by the energy of the electromagnetic field outside the boundary and then the gravitational surface redshift becomes zero from (71) for this case \(\alpha =3\).

In Table 1, we determine some \(\alpha \) values in the model for some specific mass–radius relations in the literature. As we see from Eq. (68) each \(\alpha \) gives a mass–radius ratio. Then taking also the observed mass values of some neutron stars from the literature we can find the corresponding values of the parameters such as the boundary radius, charge–radius ratio, and redshift.

5 Conclusion

We have analyzed the exact solutions of the non-minimally coupled \(Y(R)F^2\) theory for the the radiation fluid stars which have the equation of state \(\rho = 3 p\), assuming the existence of a one-parameter group of conformal motions. We have found new solutions which lead to regular metric functions and regular Ricci scalar inside the star. We have obtained non-negative matter density \(\rho \) and pressure p which vanish at the boundary of the star \(r=r_b\), \(\rho = 3 p = \frac{r_b^{\alpha } -r^\alpha }{\kappa ^2 r^2 r_b^2}\). The derivatives of the density and pressure are negative as required for an acceptable interior solution, that is, \(\frac{\mathrm{{d}}\rho }{\mathrm{{d}}r} = 3 \frac{\mathrm{{d}}p}{\mathrm{{d}}r} = - \frac{(\alpha -2)r^\alpha + 2r_b^\alpha }{\kappa ^2r_b^\alpha r^3} \) (where \(\alpha >2\)). The speed of sound \((\frac{\mathrm{{d}}p}{\mathrm{{d}}\rho } )^{1/2} = \frac{1}{\sqrt{3}} < 1\) satisfies the implication of causality, since it does not exceed the speed of light \( \mathtt {c} =1\). But the mass density \(\rho \) and charge density \(\rho _e\) have singularity at the center of the star as the same feature in [19]. However, this feature is physically acceptable since the total charge and mass became finite for the model.

Table 1 Some values of \(\alpha \) and the corresponding other parameters for some given mass and mass–radius relations of neutron stars
Full size table

After obtaining the exterior and interior metric solutions of the non-minimal theory, we matched them at the boundary \(r_b\). Using the vanishing pressure condition and total charge at the boundary, we obtained the square of the total charge–radius ratio \(\frac{\kappa ^2Q^2}{r_b^2}\), the mass–radius ratio \(\frac{M}{r_b}\), and the gravitational surface redshift z depending on the parameter \(\alpha \) of the model. Taking the limit \(\alpha \rightarrow \infty \), we found the ratio \(\frac{\kappa ^2Q^2}{r_b^2}\), which has the upper bound \(\frac{1}{3\sqrt{3} }\approx 0.1924\) and the mass–radius ratio which has the upper bound \( \frac{M}{r_b} = \frac{1}{3} + \frac{1 }{6\sqrt{3}} \approx 0.4295\). We note that this maximum mass–radius ratio is smaller than the bound which was found by Mak et al. [43] for charged general relativistic objects even also Buchdahl bound 4 / 9 [44] for uncharged compact objects. Also we found the upper limit \(z = \sqrt{3} -1 \approx 0.732\) for the gravitational surface redshift in the non-minimal model and it satisfies the bound given in [43] for charged stars. On the other hand the minimum redshift \(z=0\) corresponds to the parameter \(\alpha =3\). We have plotted all these quantities in dependence on the parameter \(\alpha \).

We determined some values of the parameter \(\alpha \) in Table 1 for some specific mass–radius relations given by the literature. Also using the observed mass values we found the corresponding parameters such as the boundary radius, charge–radius ratio, and redshift for some known neutron stars. It would be interesting to generalize the analysis to the extended theories of gravity [20, 62] coupled to the Maxwell theory in future studies.