CGC/saturation approach for high energy soft interactions: ‘soft’ Pomeron structure and $v_{n}$ in hadron and nucleus collisions from Bose–Einstein correlations

Abstract

In the framework of our model of soft interactions at high energy based on the CGC/saturation approach, we show that Bose–Einstein correlations of identical gluons lead to large values of $v_n$. We demonstrate how three dimensional scales of high energy interactions, hadron radius, typical size of the wave function in diffractive production of small masses (size of the constituent quark), and the saturation momentum, influence the values of BE correlations, and in particular, the values of $v_n$. Our calculation shows that the structure of the ‘dressed’ Pomeron leads to values of $v_n$ which are close to experimental values for proton–proton scattering, 20 % smaller than the observed values for proton–lead collisions and close to lead–lead collisions for 0–10 % centrality. Bearing this result in mind, we conclude that it is premature to consider that the appearance of long range rapidity azimuthal correlations are due only to the hydrodynamical behaviour of the quark–gluon plasma.

1 Introduction

In Ref. [1] we showed that Bose–Einstein correlations lead to strong azimuthal angle correlations, which do not depend on the difference in rapidity of the two produced hadrons (long range rapidity LRR correlations). The mechanism suggested by us has a general origin, and thus manifests itself in hadron–hadron, hadron–nucleus and nucleus–nucleus interactions, and it generates the correlation that has been observed experimentally [2–25]. The fact that Bose–Einstein correlations lead to strong LRR azimuthal angle correlations, was found long ago in the framework of Gribov Pomeron calculus [26, 27], and it has been re-discovered recently in Refs. [28–30] in the CGC/saturation approach [31]. In Ref. [1] it was noticed that these correlations give rise to $v_n$ for odd and even n, while all other mechanisms in the CGC/saturation approach, including the correlations observed in [28–30], generate only $v_n$ with even n.

The LRR correlations in the CGC/saturation approach originate from the production of two parton showers (see Fig. 1). The double inclusive cross section is described by the Mueller diagram of Fig. 1b, in which the production of gluons from the parton cascade is described by the exchange of the BFKL Pomeron (wavy double line in Fig. 1b), while, due to our poor theoretical knowledge of the confinement of quarks and gluons, the upper and lower blobs in Fig. 1b require modelling.

Fig. 1

Production of two gluons with $(y_1,\varvec{{p}}_{T1})$ and $(y_2,\varvec{{p}}_{T2})$ in two parton showers (a). b The double inclusive cross section in the Mueller diagram technique [36]. The wavy lines denote the BFKL Pomerons [37–40]

Fig. 2

Production of two identical gluons with $(y_1,\varvec{p}_{T1})$ and $(y_2,\varvec{p}_{T2})$ in two parton showers. The diagrams in the Mueller diagram technique [36] are shown in a and b. The wavy lines denote the BFKL Pomerons [37–40]

If the two produced gluons have the same quantum numbers, one can see that in addition to the Mueller diagram for different gluons (see Fig. 1b), we need to take into account a second Mueller diagram of Fig. 2b, in which two gluons with $(y_1,\varvec{{p}}_{T2})$ and $(y_2,\varvec{{p}}_{T1})$ are produced. When $\varvec{{p}}_{T1} \rightarrow \varvec{{p}}_{T2}$, the two production processes become identical, leading to the cross section $\sigma \left( \text{ two } \text{ identical } \text{ gluons }\right) = 2 \sigma \left( \text{ two } \text{ different } \text{ gluons }\right)$, as one expects. When $|\varvec{{p}}_{T2} - \varvec{{p}}_{T1}| \gg 1/R$, where R is the size of the emitter [32], the interference diagram becomes small and can be neglected.

The angular correlation emanates from the diagram of Fig. 2b, in which the upper BFKL Pomerons carry momentum $\varvec{{k}} - \varvec{{p}}_{T,12}$ with $\varvec{{p}}_{T, 12}=\varvec{{p}}_{T1}- \varvec{{p}}_{T2}$, while the lower BFKL Pomerons have momenta $\varvec{{k}}$. The Mueller diagrams for the correlation between two gluons are shown in Fig. 2.

After integration over $k_T$, the sum of diagrams Fig. 2a and b can be written as

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\left( \mathrm{identical}\,\, \mathrm{gluons}\right) \,\, \nonumber \\&\quad =\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\left( \mathrm{different}\,\, \mathrm{gluons}\right) \nonumber \\&\qquad \times \left( 1 + C\left( R |{\varvec{p}}_{T2} - {\varvec{p}}_{T1}|\right) \right) ; \end{aligned}$$

(1)

Eq. (1) coincides with the general formula for the Bose–Einstein correlations [32–35]

$$\begin{aligned} \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\left( \mathrm{identical\,\, gluons}\right) \propto { \langle } 1+e^{i r_\mu Q_\mu }{\rangle } \end{aligned}$$

(2)

where averaging $\langle \cdots \rangle$ includes the integration over $r_\mu = r_{1,\mu } - r_{2,\mu }$. There is only one difference: $Q_\mu = p_{1.\mu } -p_{2,\mu }$ degenerates to $\varvec{{Q}}\,\equiv \,\varvec{{p}}_{T,12}$, due to the fact that the production of two gluons from the two parton showers do not depend on the rapidities. Note, that the contribution of Fig. 2b does not depend on the rapidity difference $y_1 - y_2$ nor on $y_1$ and $y_2$. For $y_1=y_2$ Eq. (1) follows directly from the general Eq. (2), and the interference diagram of Fig. 3b leads to Eq. (1), and allows us to calculate the typical correlation radius and the correlation function $C\left( R |\varvec{{p}}_{T2} - \varvec{{p}}_{T1}|\right)$. On the other hand, for $y_1 \ne y_2$ but for $\varvec{p}_{T1} = \varvec{{p}}_{T,2}$ Eq. (1), gives a constant which does not depend on $y_1$ and $y_2$. However, in general case $y_1 \ne y_2$ and $\varvec{{p}}_{T1} \ne \varvec{{p}}_{T,2}$ the diagram of Fig. 2b looks problematic,¹ since it seems to describe the interference between two different final states. In Appendix A we demonstrate that the contribution of Fig. 2b does not vanish even in this general case. Note that, for $y_1 = y_2$, the sum of two Mueller diagrams, indeed, relates to the interference between two diagrams, as is shown in Fig. 3a and b. For these kinematics, as we have mentioned

$$\begin{aligned} C\left( R |{\varvec{p}}_{T2} - {\varvec{p}}_{T1}|\right) = { \langle } e^{i {\varvec{r}}_T\cdot {\varvec{Q}}_T}{\rangle }\quad \text{ where }\quad {\varvec{Q}}_T={\varvec{p}}_{T,12}. \end{aligned}$$

(3)

For $\varvec{{p}}_{T1} = \varvec{{p}}_{T2}$, the sum of two Mueller diagrams can also be viewed as the interference of the two diagrams of Fig. 3c and d, leading to

$$\begin{aligned} C\left( | 0 |\right) = { \langle } e^{i {\varvec{r}}^+ {\varvec{Q}}_-\,+i {\varvec{r}}^-\, {\varvec{Q}}_+}{\rangle } \end{aligned}$$

(4)

The calculation of the Mueller diagram shows that this average does not depend on $y_1$ and $y_2$.

Fig. 3

The interferences between two states for the production of two identical gluons in two specific cases: $y_1=y_2$ (a, b) and $\varvec{p}_{T1} = \varvec{p}_{T2}$ (c, d)

Remembering that for two parton showers in each order of perturbative QCD (or, in other words, at fixed multiplicity of the produced gluons) the amplitude can be written in the factorized form $A = A_L\left( r_+, r_-\right) \,A_T\left( \varvec{{r}}_T\right)$ leading to

$$\begin{aligned} { \langle } e^{i r_\mu \,Q_\mu }{\rangle } =\underbrace{{ \langle } e^{i \varvec{{r}}_T\cdot \varvec{{Q}}_T}{\rangle }}_{\text{ averaging } \text{ over } r_T} \times \underbrace{{ \langle } e^{i \varvec{{r}}^+\, \varvec{{Q}}_- + i \varvec{{r}}^-\, \varvec{{Q}}_+} {\rangle }}_{\text{ averaging } \text{ over } \, r_+, r_-}. \end{aligned}$$

(5)

In our opinion, the above discussion shows that the Mueller diagram of Fig. 2b does not characterize the interference between two orthogonal state but is an economical way to describe the independence of identical gluon production on rapidities, providing the smooth analytical description of the cross section from $y_1=y_2$ to the general case $y_1 \ne y_2$. Since this point is not obvious we would like to recall the main features of the leading $\mathrm{log}(1/x)$ approximation (LLA). In the LLA we account for the following kinematic region [37–40] for the production of two parton showers (see Fig. 4):

$$\begin{aligned}&\text{ first } \text{ parton } \text{ shower } \rightarrow Y>\cdots> \nonumber \\&\quad y_i>\cdots>y_{n_1}> y_1> y_{n_2}> \cdots> y_i>\cdots>0;\nonumber \\&\text{ second } \text{ parton } \text{ shower } \rightarrow Y>\cdots> y_i>\cdots> \nonumber \\&\quad y_{n_3}>y_2>y_{n_4}>\cdots> y_i> \cdots >0;\nonumber \\&\text{ parameters } \text{ of } \text{ LLA }: \bar{\alpha }_S\ll 1\,\, \bar{\alpha }_S\left( y_{i+1} - y_i\right) \ge 1;\nonumber \\&\quad \bar{\alpha }_S\left( Y - y_i\right) \ge 1;\quad \bar{\alpha }_S\left( y_i - 0 \right) \ge 1;\quad \bar{\alpha }_S\left( Y - y_1\right) \ge 1;\nonumber \\&\quad \bar{\alpha }_S\left( Y - y_2\right) \ge 1;\quad \bar{\alpha }_S\left( y_1 - 0\right) \ge 1;\nonumber \\&\quad \bar{\alpha }_S\left( y_2 - 0 \right) \ge 1;\quad \bar{\alpha }_S\left( y_1 - y_2\right) \ge 1. \end{aligned}$$

(6)

Fig. 4

The amplitude of production of $n=n_1+n_2+n_3+n_4$ particles, $A^\mathrm{different\,gluons}\left( 2 \rightarrow n | \{ y_i, p_{Ti}\}; y_1, \varvec{p}_{T1} ; y_2, \varvec{p}_{T2} \right)$ (see Eq. (7a))

The cross sections of double inclusive productions can be calculated in LLA for the production of two parton showers in the following way:

$$\begin{aligned}&{\frac{\mathrm{d}^2 \sigma ^{\text {different gluons}}}{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}} \nonumber \\&\quad =\sum ^\infty _{n_1+n_2-2>2}\,\, \sum ^\infty _{n_3+n_4-2>2} \,\int \mathrm{d}\Phi ^{(1)}_{n_1 + n_2} \mathrm{d} \Phi ^{(2)}_{n_3+n_4}\, \nonumber \\&\qquad \times |A^{\text {different gluons}} \left( \{y_i,p_{Ti}\}; y_1,p_{T1}; y_2,p_{T2}\right) |^2 \nonumber \\&\quad =\sum _{n_1+n_2 =n-2>2}^\infty \,\,\,\,\prod ^{n_1}_{Y> y_i> y_1} \nonumber \\&\quad \int ^{y_{i+1}}_{y_{i-1}} \times \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \prod ^{n_2}_{y_1> y_i> 0 } \int ^{y_{i+1}}_{y_{i-1}} \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \nonumber \\&\quad \times \,\sum _{n_3+n_4 =n'-2>2}^\infty \,\,\,\,\prod ^{n_3}_{Y> y_i> y_2} \nonumber \\&\quad \int ^{y_{i+1}}_{y_{i-1}} \times \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \prod ^{n_4}_{y_2> y_i > 0 } \int ^{y_{i+1}}_{y_{i -1}} \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \,\nonumber \\&\quad \times | \Gamma ^2 A_{n_1 n_2}\left( 2 \rightarrow n | \{ y_i, p_{Ti}\}; y_1, \varvec{p}_{T1} \right) A_{n_3 n_4}\nonumber \\&\quad \times \left( 2 \rightarrow n | \{ y_i, p_{Ti}\}; y_2, \varvec{p}_{T2} \right) ]^2 \end{aligned}$$

(7a)

$$\begin{aligned}&\xrightarrow {\text {LLA}} \sum _{n_1+n_2 =n-2>2}^\infty \,\,\,\,\prod ^{n_1}_{Y> y_i> y_1} \nonumber \\&\quad \times \int ^{y_{i+1}}_{y_{i-1}} \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \,\,\, \prod ^{n_2}_{y_1> y_i> 0 } \int ^{y_{i+1}}_{y_{i-1}} \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \nonumber \\&\quad \times \,\sum _{n_3+n_4 =n'-2>2}^\infty \,\,\,\,\prod ^{n_3}_{Y> y_i> y_2} \nonumber \\&\quad \int ^{y_{i+1}}_{y_{i-1}} \times \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \prod ^{n_4}_{y_2> y_i > 0 } \int ^{y_{i+1}}_{y_{i -1}} \mathrm{d} y_i \mathrm{d}^2 p_{T,i} \,\nonumber \\&\quad \times | \Gamma ^2 A_{n_1 n_2}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_1=0, \varvec{p}_{T1} \right) \nonumber \\&\quad \times A_{n_3 n_4}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_2=0, \varvec{p}_{T2} \right) |^2 \end{aligned}$$

(7b)

where $\mathrm{d} \Phi ^{(1)}_{n_1+n_2}$ and $\mathrm{d} \Phi ^{(2)}_{n_3+n_4}$ are the phase spaces of the produced gluons in the first and second parton showers. $A^\mathrm{different \,gluons}\left( \{y_i,p_{Ti}\}; y_1,p_{T1}; y_2,p_{T2}\right)$ = $\Gamma ^2 A_{n_1 n_2}\left( 2 \!\rightarrow \! n | \{ y_i, p_{Ti}\}; y_1, \varvec{p}_{T1} \right) A_{n_3 n_4}\left( 2 \!\rightarrow \! n | \{ y_i, p_{Ti}\}; y_2, \varvec{p}_{T2} \right)$ (see Fig. 4) and all other notations are shown in Fig. 4.

The transition from Eq. (7a) to (7b), occurs due to the fact that we want to obtain the log contribution $\propto (y_{i+1} - y_{i -1})$ for each $d y_i$, These logarithms stem from the integration of the phase space of produced particles, while we can neglect the $y_i$ dependence of the production amplitude. In other words, the production amplitudes are functions only of the transverse momenta and Eq. (7b) shows that the longitudinal degrees of freedom can be factorize out [37–40].

Equation (7a), after integrations over $y_i$, can be re-written in a more efficacious form, viz.

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} =\sum _{n_1+n_2 =n-2>2}^\infty \,\sum _{n_1+n_2 =n'-2>2}^\infty \nonumber \\&\quad \times \underbrace{ \frac{1}{n_1!} \left( Y - y_1\right) ^{n_1} \, \frac{1}{n_2!} \left( y_1 - 0\right) ^{n_2\,} \frac{1}{n_3!} \left( Y - y_2 \right) ^{n_3}\, \frac{1}{n_4!} \left( y_2 -0 \right) ^{n_4}}_\mathrm{integral\,over\,the \,longitudinal\,phase\,space}\nonumber \\&\quad \times \int \prod _i \mathrm{d}^2 p_{Ti}\, |\Gamma ^2 A_{n_1 n_2}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_1=0, \varvec{p}_{T1} \right) \nonumber \\&\quad \times A_{n_3 n_4}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_2=0, \varvec{p}_{T2} \right) |^2. \end{aligned}$$

(8)

Summing over $n_i$ we obtain the Mueller diagram of Fig. 1.

For identical particles we need to replace

$$\begin{aligned}&A^\mathrm{different \,gluons}\left( \{y_i=0,p_{Ti}\}; y_1=0,p_{T1}; y_2=0,p_{T2}\right) \,\nonumber \\&\quad = \Gamma ^2 A_{n_1 n_2}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_1=0, \varvec{p}_{T1} \right) \nonumber \\&\qquad \times A_{n_3 n_4}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_2=0, \varvec{p}_{T2} \right) \nonumber \\&\quad \rightarrow A^\mathrm{identical \,gluons}\left( \{y_i=0,p_{Ti}\}; y_1=0,p_{T1}; y_2=0,p_{T2}\right) \nonumber \\&\quad = A^\mathrm{different \,gluons}\left( \{0,p_{Ti}\}; y_1=0,p_{T1}; y_2=0,p_{T2}\right) \, \nonumber \\&\qquad +\,A^\mathrm{different \,gluons}\left( \{0,p_{Ti}\}; y_2=0,p_{T2};y_1=0,p_{T1}\right) \, \nonumber \\&\quad = \Gamma ^2 A_{n_1,n_2}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_1=0, \varvec{p}_{T1} \right) \nonumber \\&\qquad \times A_{n_3 n_4}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_2=0, \varvec{p}_{T2} \right) \,\, \nonumber \\&\qquad +\, \Gamma ^2 A_{n_1 n_2}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_2=0, \varvec{p}_{T2} \right) \nonumber \\&\qquad \times A_{n_3 n_4}\left( 2 \rightarrow n | \{ y_i=0, p_{Ti}\}; y_1=0. \varvec{p}_{T1} \right) \end{aligned}$$

(9)

We wish to stress that in Eq. (9) we use the Bose–Einstein symmetry for the production amplitudes, which are only functions of the transverse momenta of produced particles.

Such a replacement leads to the sum of the diagrams of Fig. 2a and b.

The goal of this paper is to calculate the function $\,C\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right)$, which tends to 1 at $\varvec{p}_{T2} \rightarrow \varvec{p}_{T1}$, and vanishes for $R |\varvec{p}_{T2} - \varvec{p}_{T1}| \gg 1$. To estimate $C\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right)$, it is sufficient to know the double inclusive cross section for $y_1 = y_2$, where Fig. 2b contributes significantly.

Fig. 5

The structure of $N_{\mathbb {P}h} \left( k^2_T \right)$

To obtain the double inclusive cross section, we need to add the cross section for two different gluon production, which has the form

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}=\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} \nonumber \\&\quad \left( \mathrm{different\, gluons} \right) \nonumber \\&\quad \times \left( 1+\frac{1}{N^2_c - 1}\,\,C\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right) \right) . \end{aligned}$$

(10)

In Eq. (10) we take into account that we have $N^2_c - 1$ pairs of the identical gluons, where $N_c$ is the number of colours, and that the polarizations of the identical gluons should be the same. The latter leads to a suppression of $\frac{1}{2}$ of the second term in Eq. (10). Using Eq. (10) we can find $v_n$, since

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\propto 1\nonumber \\&\quad +\, 2 \sum _n V_{ n \Delta } \left( p_{T1}, p_{T2}\right) \,\cos \left( \Delta \, \varphi \right) \end{aligned}$$

(11)

where $\Delta \varphi$ is the angle between $\varvec{p}_{T1}$ and $\varvec{p}_{T2}$. $v_n$ is determined from $V_{n \Delta } \left( p_{T1}, p_{T2}\right)$:

$$\begin{aligned}&1.~~ v_n\left( p_T\right) = \sqrt{V_{n \Delta }\left( p_T, p_T\right) }; \nonumber \\&2.~~~~ v_n\left( p_T\right) = \frac{V_{n \Delta }\left( p_T, p^\mathrm{Ref}_T\right) }{\sqrt{V_{n \Delta }\left( p^\mathrm{Ref}_T, p^\mathrm{Ref}_T\right) }}; \end{aligned}$$

(12)

Eqs. (12)-1 and (12)-2 depict two methods of how the values of $v_n$ have been extracted from the experimentally measured $V_{n \Delta } \left( p_{T1}, p_{T2}\right)$. $p^\mathrm{Ref}_T$ denotes the momentum of the reference trigger. These two definitions are equivalent if $V_{n \Delta }\left( p_{T1}, p_{T2}\right)$ can be factorized as $V_{n \Delta }\left( p_{T1}, p_{T2}\right) = v_n\left( p_{T1}\right) \,v_n\left( p_{T2}\right)$. We will show below that in our approach this is the case for the restricted kinematic region $R\,p_{Ti}\ll 1$.

The first problem that we face in calculating $C\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right)$, is to estimate the value of R, which increases with energy (see for example LHC data of Refs. [41–44]). On the other hand, the BFKL Pomeron [37–40] does not lead to the shrinkage of the diffraction peak, as it has no slope for the Pomeron trajectory. The only way to obtain a size which increases with energy is to use the unitarity constraints, $A^\mathrm{BFKL} \left( Y,b\right) \propto e^{\Delta _\mathrm{BFKL} \,Y} a(b)< 1$ [45, 46], where $\Delta _\mathrm{BFKL}$ is the intercept of the BFKL Pomeron and b is the impact factor. However, in QCD $a\left( b\right)$ decreases as a power of b and the unitarity constraints lead to $R \propto \exp \left( \Delta _\mathrm{BFKL}\,Y\right)$ [28]. Therefore, to obtain the energy behaviour of R, we need to introduce a non-perturbative correction at large b, which ensures $a(b) \propto \exp \left( - \mu _\mathrm{soft} b\right)$, and we also to take into account the multi Pomeron interactions which satisfy the unitarity constraints. Fortunately, the second part of the problem has been solved in the CGC/saturation approach [31], but the first needs modelling of the unknown confinement of quarks and gluons. Hence, we are doomed to build a model which includes everything that we know theoretically regarding the CGC/saturation approach, but in addition, one needs to introduce some phenomenological descriptions of the hadron structure, and the large b behaviour of the BFKL Pomeron.

Such a model for hadron–hadron interactions at high energy has been developed in Refs. [49–52], and it successfully describes the experimental data on total, inelastic and diffractive cross sections, as well as the inclusive production and LRR correlations. The goal of this paper is to show that the structure of the ‘dressed’ Pomeron in this model leads to strong BE correlations, and generates $v_n$ both for even and odd n, in hadron and nucleus interactions. In the next section we consider the contribution to $C( R |\varvec{p}_{T2} - \varvec{p}_{T1}|)$ from the first Mueller diagram, and discuss the different sources of BE correlations. In Sect. 3 we give a brief review of the structure of the Pomeron in our model, in which we incorporate the solution to the CGC/saturation equations with additional non-perturbative assumptions: the large b behaviour for the saturation momentum, and the structure of the hadrons. It has been known for a long time [26, 27, 53–55] in the framework of Gribov Pomeron calculus and has been re-considered in the CGC/saturation approach [56, 56–63] that the LRR correlations stem from the production of gluon jets from two different parton showers (see Fig. 1). In Sect. 4 we evaluate the BE correlations that result from the dressed Pomeron of our model, and show that they are able to describe the main features of the experimental data.

2 Calculation of the first diagram

2.1 Proton–proton scattering

The first Mueller diagram which contributes to $C( R |\varvec{p}_{T2} - \varvec{p}_{T1}|)$, and which we need to calculate, is shown in Fig. 2e and can be written in the form [64]:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}= \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}}\left( \mathrm{different}\, \mathrm{gluons} \right) \nonumber \\&\qquad \times \left( \frac{1}{N^2_c - 1}\,\,C\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right) \right) \nonumber \\&\quad =\, \left( \frac{\bar{\alpha }_S\,C_F}{2 \pi }\right) ^2 \int \mathrm{d}^2 k_T \,N_{\mathbb {P}h}\left( k^2_T\right) \, \nonumber \\&\qquad \times N_{\mathbb {P}h}\left( \left( \ \varvec{k_T} + \varvec{p}_{T,12}\right) ^2\right) \, \frac{\mathrm{d} \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}} \nonumber \\&\qquad \times \left( k_T, | \varvec{k_T} + \varvec{p}_{T,12}|\right) \frac{\mathrm{d} \sigma }{\mathrm{d} y_2 \mathrm{d}^2 p_{T2}}\left( k_T, | \varvec{k_T} + \varvec{p}_{T,12}| \right) \end{aligned}$$

(13)

where $\varvec{p}_{T,12} = \varvec{p}_{T1} -\varvec{p}_{T2}$ and

$$\begin{aligned}&\frac{\mathrm{d} \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}}\left( k_T, | \varvec{k_T} + \varvec{p}_{T,12}|\right) \nonumber \\&\quad =\,\int \mathrm{d}^2 q_T\, \phi ^\mathrm{BFKL}\left( q_T,\varvec{k}_T - \varvec{q}_T\right) \,\Gamma _\mu \left( q_T, p_{T1}\right) \nonumber \\&\qquad \times \Gamma _\mu \left( \varvec{k}_T - \varvec{q}_T, p_{T2}\right) \,\phi ^\mathrm{BFKL}\left( q_T,\varvec{k}_T + \varvec{p}_{T,12} - \varvec{q}_T\right) \nonumber \\ \end{aligned}$$

(14)

In Eq. (14) $\phi ^\mathrm{BFKL}$ denotes the parton density of the BFKL Pomeron, with momentum transferred by the Pomeron $\varvec{k}_T$ or $\varvec{k}_T + \varvec{p}_{T,12}$. The Lipatov vertex $\Gamma _\mu$, as well as the equations for $\phi ^\mathrm{BFKL}$ will be discussed in Appendix A. Generally speaking, $N_{\mathbb {P}h}$ has a structure which is shown in Fig. 5:

$$\begin{aligned} N_{\mathbb {P}h}\left( k^2_T\right)= & {} \sum ^{M_0}_{M_n}\,g^2_{\mathbb {P}n}\left( k^2_T\right) \delta \left( M^2 - M^2_{n}\right) \nonumber \\&+\,g_{\mathbb {P}h}\left( 0\right) \,G_{3 \mathbb {P}}\left( k^2_T\right) \, e^{\Delta _\mathrm{BFKL} Y} \end{aligned}$$

(15)

where $M_n$ denotes the mass of the resonances, $\Delta _\mathrm{BFKL}$ the intercept of the BFKL Pomeron, and $G_{3 \mathbb {P}}$ the triple Pomeron vertex. Considering the contribution of the first term to $N_{\mathbb {P}h}$, we can neglect, in the first approximation, the dependence of $\phi ^\mathrm{BFKL}$ on the momentum transferred, since $Q_T$ turns out to be of the order of the saturation momentum $Q_s \gg 1/R_h$, where $R_h$ is the hadron size incorporated in $N_{\mathbb {P}h}$.

Fig. 6

$v_n$ versus $p_T$ for proton–proton scattering at $W = 13\,\mathrm{TeV}$, using Eqs. (12) and (19). a $v_n$ that stem from Eq. (12)-1. In b the estimates from Eq. (12)-2 for $p^\mathrm{Ref}_T = 2 \,\mathrm{GeV}$ are plotted. c The same $v_n$ as in b, where $p^\mathrm{Ref}_T$ is taken in the interval 0.5–5 GeV, as is measured in Ref. [21]

This is not the case for the second term in Eq. (15), which has $Q_T \sim Q_s$. It leads to the BFKL Pomeron calculus which takes the Pomeron interactions into account. We will discuss this contribution in Sects. 3 and 4. In this section we restrict ourselves to the first term in the sum in Eq. (5). Collecting all formulae, we find that in the first diagram

$$\begin{aligned}&C\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right) \propto \int \mathrm{d}^2 k_T \,g^2_{\mathbb {P},\mathrm{pr}} \left( k^2_T\right) \, g^2_{\mathbb {P},\mathrm{tr}} \left( \left( \varvec{k} - \varvec{p}_{T,12}\right) ^2\right) {\bigg /} \nonumber \\&\quad \times \int \mathrm{d}^2 k_T \,g^2_{\mathbb {P},\mathrm{pr}} \left( k^2_T\right) \, g^2_{\mathbb {P},\mathrm{tr}} \left( k^2_T\right) . \end{aligned}$$

(16)

To obtain the first estimates for the vertices of the soft Pomeron interaction with the projectile and target, we use the following parameterizations:

$$\begin{aligned} g_\mathrm{pr}( k^2) = g^0_\mathrm{pr}\,e^{- \frac{1}{2}B_\mathrm{pr}\,k^2_T};\quad g_\mathrm{tr}( k^2) = g^0_\mathrm{tr}\,e^{- \frac{1}{2}B_\mathrm{tr}\,k^2_T}. \end{aligned}$$

(17)

For proton–proton collisions we take $B_\mathrm{pr} = B_\mathrm{tr} = B$.

In this case [1, 26, 27]

$$\begin{aligned}&C\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right) \nonumber \\&\quad =\exp \left( - B_R\,\left( p^2_{T1} - 2 p_{T1} p_{T2} \cos \left( \Delta \varphi \right) + p^2_{T2}\right) \right) \end{aligned}$$

(18)

with $B_R = B_\mathrm{pr} B_\mathrm{tr}/\left( B_\mathrm{pr} + B_\mathrm{tr}\right)$. $B_R = \frac{1}{2}B$ for proton–proton scattering.

In Ref. [1] it is shown that Eq. (18) leads to $V_{\Delta n}$ of Eq. (11) which is equal to

$$\begin{aligned}&V_{\Delta \, n} = I_n\left( 2 B_R p_{T1} p_{T2}\right) \nonumber \\&\quad \times \frac{e^{-B_R\left( p^2_{T1} + p^2_{T2}\right) }}{N^2_C - 1 + I_0\left( 2 B_R p_{T1} p_{T2}\right) \,e^{-B_R\left( p^2_{T1} + p^2_{T2}\right) }} \end{aligned}$$

(19)

where $I_n$ is the modified Bessel function of the first kind.

In Fig. 6 taking $B_R = 5 \,\mathrm{GeV}^{-2}$, we plot the prediction for $v_n$ using Eqs. (12) and (19). This value of $B_R$ corresponds to the slope of the elastic cross section for proton–proton scattering at $W = 13\,\mathrm{GeV}$. One can see that Eq. (12)-1 and (12)-2 give different predictions, demonstrating that we do not have factorization $V_{n \Delta }\left( p_{T1}, p_{T2}\right) \ne v_n\left( p_{T1}\right) \,v_n\left( p_{T2}\right)$. Fig. 6c shows $v_n$ for $p^\mathrm{min}_T \le p_{T2} = p^\mathrm{Ref}_{T} \le p^\mathrm{max}_T$ with $p^\mathrm{min}_T =0.5 \,\mathrm{GeV}$ and $p^\mathrm{max}_T = 5 \,\mathrm{GeV}$, as done in Ref. [21]. To calculate such a $v_n$, we need to know the dependence of the cross section on $p_{T2}$. Indeed, we need to take Eq. (10) and integrate it over $p_{T2}$: viz.

$$\begin{aligned}&H\left( p_{T1},\Delta \varphi \right) = \int ^{p^\mathrm{max}_{T2}}_{p^\mathrm{min }_{T2}} \mathrm{d} p^2_{T2}\, \frac{\mathrm{d}^2 \sigma {(\mathrm{Eq.(10}))}}{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} \nonumber \\&\quad \propto 1 + 2 \sum _n V_{ n \Delta } \left( p_{T1}\right) \,\cos \left( \Delta \,\varphi \right) . \end{aligned}$$

(20)

For Fig. 6c, we need to know the behaviour of the double inclusive cross section on $p_{T1}$ and $p_{T2}$. We assume that $\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2\, \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} \propto 1/\left( p^2_{T1}\, p^2_{T2}\right)$ for the cross sections given by Fig. 1b and by Fig. 2c and d. In Appendix A we show that the cross section for Fig. 2e $\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2\, \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} \left( (\mathrm{Fig}. 2{\text {-}}\mathrm{e})\right) \propto \big ( 1/p^2_{T1} + 1/p^2_{T2}\big )^2$.

We took the energy dependence into account by calculating the $B_R$ from the slope of the elastic scattering at given energy W, which was taken from Ref. [49].

Fig. 7

$v_2$ versus $p_T$ for proton–proton scattering at $W=2.76\,\mathrm{TeV}$ and at $W = 13\,\mathrm{TeV}$. a $v_n$ that stem from Eq. (12)-2 for $p^\mathrm{Ref}_T$, which is taken in the interval 0.5–5 GeV, as is measured in Ref. [21]. b The experimental data taken from Ref. [21]

One can see that the calculated values, as well as energy dependence (Fig. 7) are close to the experimental data of Ref. [21]. The main difference is in the $p_T$ dependence, which suggests the necessity to include the diffractive dissociation process or, in other words, the entire sum in Eq. (15), as well as the enhanced diagrams that are generated by the BFKL Pomeron calculus (see Fig. 5).

We can estimate the sum over resonances or, in other words, the diffraction production of states with low mass, by using our model (see Appendix B for necessary formulae). In Fig. 8 we plot the correlation function $C\left( p_{T,12}\right)$ as defined in Eq. (10) for $|\varvec{p}_{T1}|=|\varvec{p}_{T2}|$, which is the result of these calculations. One can see that the effective $p_{T,12}$ dependence of the slope, turns out to be much smaller than our estimates from the first diagrams that we obtained above. The slope that we used for the calculation shown in Fig. 6 was estimated as $\frac{1}{4}B_\mathrm{el}$, where $B_\mathrm{el} = 20\,\mathrm{GeV}^{-2}$ is the slope of the elastic cross section at $W = 13 \,\mathrm{TeV}$. We see two reasons for such a drastic change in the $p_{T,12}$ dependence: first, we took into account the diffractive production processes which were neglected in Fig. 6; and second, in our model the effective shrinkage of the diffraction peak originates from the shadowing corrections, as the BFKL Pomeron has no inherent shrinkage. Such corrections are stronger in net diagrams of Fig. 14b that are responsible for elastic scattering than for the fan diagrams of Fig. 25 that contribute to inclusive production. Recall that $B_\mathrm{shr}\approx 10\, \mathrm{GeV}^{-2}$ at $W = 13 \,\mathrm{TeV}$, comes from the shrinkage of the diffraction peak.

Fig. 8

Correlation function $C\left( p_{T,12}\right)$ as it is defined in Eq. (10), versus $p_{T,12} = |\varvec{p}_{T1} - \varvec{p}_{T2}|$. Dashed line corresponds to $\exp ({-}B p^2_{T,12})$ with $B = 1.7 \,\mathrm{GeV}^{-2}$, while the dotted line shows the dependence that we used in Sect. 2 to calculate the first diagram: $\exp ({-}B\,p^2_{T,12})$ with $B = 5 \,\mathrm{GeV}^{-2}$

The calculation of $v_n$ are shown in Fig. 9. One can see that we obtain large $v_n$ for both odd and even n. The value of $v_2$ from Fig. 9c is about 10 % larger, than the experimental one from Ref. [21] (see Fig. 7b). However, our calculations lead to narrower distributions in $p_T$ than the experimental one. The factorization $V_{n \Delta }\left( p_{T1}, p_{T2}\right) = v_n\left( p_{T1}\right) \,v_n\left( p_{T2}\right)$ is strongly violated, as in the case of estimates of the first diagram.

Fig. 9

$v_n$ versus $p_T$ for proton–proton scattering at $W = 13\,\mathrm{TeV}$, using Eqs. (B9) and (12). a $v_n$ that stem from Eq. (12)-1. In b the estimates from Eq. (12)-2 for $p^\mathrm{Ref}_T = 2 \,\mathrm{GeV}$ are plotted. b The same $v_n$ as in Fig. 6c but $p^\mathrm{Ref}_T$ is taken in the interval 0.5–5 GeV, as is measured in Ref. [21]

Figure 7 illustrates the energy dependence of $v_n$ for proton–proton scattering, showing $v_2$ for two energies $W=2.56 \,\mathrm{TeV}$ and $W=13 \,\mathrm{TeV}$. Note that $v_2$ does not depend on energy, in accord with the experimental data of Ref. [21].

Therefore, we can conclude that the first term in Eq. (15) leads to a value of $v_n$, which is large and of the order of the experimental one; the inclusion of diffraction in the region of small mass (sum over resonances in Eq. (15) leads to a decrease of the interaction volume, but cannot reproduce the experimental $p_T$ distributions of $v_n$, and BE correlations show the experimentally observed independence on energy.

Fig. 10

a Comparison Eq. 22 with the same equation where $S_A^2(k^2_T)$ is replaced by $\delta (k_T)$. $R_A = 6.5\,\mathrm{fm}$ for gold. $B = 10 \,\mathrm{GeV}^{-2}$ for proton at $W =13$ TeV. b Correlation function $C(p_{T,12})$ for proton–lead scattering at $W = 5$ TeV in our model (see Appendix C) as it is defined in Eq. (10), versus $p_{T,12} = |\varvec{p}_{T1} - \varvec{p}_{T2}|$. Dashed line corresponds to $\exp ({-} B p^2_{T,12})$ with $B=4.2 \,\mathrm{GeV}^{-2}$, while the dotted line shows the dependence that we used in Sect. 2 to calculate the first diagram: $\exp ({-} B\,p^2_{T,12})$ with $B = 10 \,\mathrm{GeV}^{-2}$

Fig. 11

$v_n$ versus $p_T$ for proton–gold (a–c) scattering at $W = 13 \,\mathrm{TeV}$ and proton–lead scattering at $W = 5\,\mathrm{TeV}$ (c, d), using Eqs. (12) and (19). a, d $v_n$ that stem from Eq. (12)-1. In b and e the estimates from Eq. (12)-2 for $p^\mathrm{Ref}_T = 2 \,\mathrm{GeV}$ are plotted. c, f The same $v_n$ as in Fig. 6c but $p^\mathrm{Ref}_T$ is taken in the interval 1–3 GeV as it is measured in Ref. [22–25]

2.2 Hadron–nucleus and nucleus–nucleus interaction

For a nucleus we can simplify the calculation, considering cylindrical nuclei which have a form factor

$$\begin{aligned} S_A\left( k_T\right) = \frac{R_A}{k_T}\,J_1\left( k_T R_A\right) \end{aligned}$$

(21)

where $J_1$ is the Bessel function. Taking Eq. (21) into account one can see that

$$\begin{aligned}&C_{pA}\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right) \propto \int \mathrm{d}^2 k_T \, g^2_{\mathbb {P},\mathrm{tr}} \left( \left( \varvec{k}_T - \varvec{p}_{T,12}\right) ^2\right) \nonumber \\&\qquad \,S_A^2 \left( k^2_T\right) {\bigg /}\int \mathrm{d}^2 k_T \, g^2_{\mathbb {P},\mathrm{tr}} \left( \left( k^2_T\right) ^2\right) \,S_A^2\left( k^2_T\right) \nonumber \\&\quad =\int \mathrm{d}^2 k_T \, e^{-B\left( k^2_T + p^2_{T,12}\right) } \,I_0\left( 2 B \,k_T\, p_{T,12}\right) \,\nonumber \\&\qquad S_A^2 \left( k^2_T\right) {\bigg /}\int \mathrm{d}^2 k_T \,\, e^{ - B k^2_T} \,\,S_A^2\left( k^2_T\right) . \end{aligned}$$

(22)

We expect that $S_A\left( k_T\right)$ leads to small $k_T \sim 1/R_A$, since the radius of nucleus is large. In Fig. 10a we compare Eq. (22) with $\exp \,(- B p^2_{T,12})$, which follows from Eq. (22), replacing $S_A^2\left( k^2_T\right)$ by $\delta \left( k_T\right)$. The agreement is impressive.

Fig. 12

$v_n$ versus $p_T$ for proton–lead scattering at $W = 5\,\mathrm{TeV}$ measured by ATLAS collaboration [21] (Fig. 9 from this paper)

Fig. 13

$v_n$ versus $p_T$ for gold–gold scattering at $W = 13\,\mathrm{TeV}$, using Eqs. (12) and (19). a $v_n$ that stem from Eq. (12)-1. In b the estimates from Eq. (12)-2 for $p^\mathrm{Ref}_T = 2 \,\mathrm{GeV}$ is plotted. c, d The difference between proton–gold and gold–gold interactions

In Fig. 11 we plot the prediction for proton–gold scattering. One can see that the Bose–Einstein correlations generate large $v_n$ for $n \ge 3$. Actually, we have several mechanisms (see, for example, review of Ref. [65]) for $v_n$ with even n, therefore, it is instructive to note that the simple estimates in this section lead to large $v_{2n - 1}$, larger than has been measured [22–25]. It should be stressed that using a more general approach which includes the diffractive production of small masses, as well as the shadowing corrections that lead to the shrinkage of diffractive peak, we obtain the predictions (see formulae in Appendix C) which repeat the main features of our estimates in the simple model of Eq. (22). These calculations are plotted in Fig. 11d–f. In Fig. 10b estimates for $C( p_{T,12})$ in our model (see Appendix C) are shown. One can see that $C( p_{T,12})$ are different, and the model gives a smaller interaction volume. However, all qualitative features turn out to be the same: larger interaction volume than for proton–proton scattering, $v_2$ is much smaller than the experimental value (see Fig. 12); $v_3$, $v_4$ and even $v_5$ are close to the experimental values; and the value of the typical $p_T$ is about $1 \,\mathrm{GeV}$ instead of $p_T = 3$–4 GeV in the experimental data.

For the nucleus–nucleus interaction $C_{AA}\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right)$ takes the form

$$\begin{aligned}&C_{AA}\left( R |\varvec{p}_{T2} - \varvec{p}_{T1}|\right) \propto \int \mathrm{d}^2 k_T \, S_A^2 \left( \left( \varvec{k}_T - \varvec{p}_{T,12}\right) ^2\right) \, \nonumber \\&\quad \times S_A^2\left( k^2_T\right) {\bigg /} \int \mathrm{d}^2 k_T \, S^2_A \left( \left( k^2_T\right) ^2\right) \,S_A^2\left( k^2_T\right) ; \end{aligned}$$

(23)

Fig. 13 shows $v_n$ for gold–gold scattering. One can see three major differences: $v_n$ values turns out to be smaller than for proton–nucleus scattering, especially when $p_{T2} = p^\mathrm{Ref}_T$ differs from $p_{T1}$; the momentum distribution is much narrower than for pA scattering, and $v_n$ are the same for all n.

Comparing Figs. 6, 11 and 13 we can conclude that the simplest estimates lead to sufficiently large $v_n$ for both even and odd n, which are similar to those obtained in proton–proton and proton–nucleus collisions, but they are considerably smaller for the nucleus–nucleus case. Comparing these predictions with the experimental data of Refs. [2–25] we see that the BE correlations should be taken into account in all three reactions, since they give sizable contributions.

3 A brief review of our model

In this section we will give a brief review of our model which has been developed in Refs. [49, 50]. The advantage of the model is that it describes the experimental data on diffractive and elastic production [49]; the inclusive production [51] and large rapidity range (LRR) correlations [52].

Fig. 14

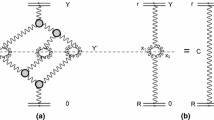
a The set of the diagrams in the BFKL Pomeron calculus that produce the resulting (dressed) Green function of the Pomeron in the framework of high energy QCD. The red blobs denote the amplitude of dipole–dipole interaction at low energy. In b the net diagrams, which include the interaction of the BFKL Pomerons with colliding hadrons, are shown. The sum of the diagrams after integration over positions of $G_{3 \mathbb {P}}$ in rapidity, reduces to c

As has been mentioned we need to build a model which incorporates at least two non-perturbative phenomena: the correct large b behaviour of the amplitude (see Refs. [47, 48]) and the hadron structure. These need to be incorporated so as to reproduce in the framework of one approach, the main features of the experimental data, such as the increase of the interaction radius with energy, a sufficiently large cross section of diffraction production, as well as energy and multiplicity dependence of inclusive cross sections and two particle correlations. On the other hand, we wish to include as much information as possible from a theoretical approach based on QCD.

3.1 Theoretical input and ‘dressed’ Pomeron Green function

At the moment, the effective theory for QCD at high energies exists in two different formulations: the CGC/saturation approach [66–82], and the BFKL Pomeron calculus [37, 38, 83–105]. In building our model we rely on the BFKL Pomeron calculus, since the relation to diffractive physics is more evident in this approach. However, we are aware that the CGC/saturation approach gives a more general pattern [101–104]. In Refs. [103, 104] it was proven that these two approaches are equivalent for

$$\begin{aligned} Y \le \frac{2}{\Delta _{{\tiny \mathrm{BFKL}}}}\,\ln \left( \frac{1}{\Delta ^2_{ {\tiny \mathrm{BFKL}}}}\right) \end{aligned}$$

(24)

where $\Delta _{{\tiny \mathrm{BFKL}}}$ denotes the intercept of the BFKL Pomeron. As we will see, in our model $\Delta _{{\tiny \mathrm{BFKL}}} \approx 0.2$–0.25 leading to $Y_\mathrm{max} = 20$–30, which covers all accessible energies. In addition in Refs. [103, 104] it is shown that for such Y, we can safely use the Mueller–Patel–Salam–Iancu (MPSI) approach [106–109], which allows us to calculate the contribution to the resulting BFKL Pomeron Green function (see Fig. 14a):

$$\begin{aligned}&G^{{\tiny \mathrm{dressed}}}_\mathbb {P}\left( Y, r, R; b \right) \nonumber \\&\quad =\int \prod _{i =1} \mathrm{d}^2 r_i\, \mathrm{d}^2 b_i\, \mathrm{d}^2 r'_i\, \mathrm{d}^2 b'_i\, N\left( Y- Y', r, \{ r_i,b - b_i\}\right) \, \nonumber \\&\qquad \times A^\mathrm{BA}_{{\tiny \mathrm{dipole-dipole}} }\left( r_i, r'_i, \varvec{b}_i - \varvec{b'}_i\right) N\left( Y', R, \{ r'_i,b'_i\}\right) \nonumber \\ \end{aligned}$$

(25)

where $A^{BA}_{{\tiny \mathrm{dipole-dipole}}}$ is the dipole–dipole scattering amplitude in the Born approximation of perturbative QCD, and is shown in Fig. 14a by the red circles.

We need to find the amplitude for the production of dipoles of size $r_i$ at impact parameters $b_i$. This amplitude can be written as (see Fig. 14c)

$$\begin{aligned}&N\left( Y- Y', r, \{ r_i,b_i\}\right) \nonumber \\&\quad = \sum ^{\infty }_{n=1} \,\left( - \,1\right) ^{n+1} \widetilde{C}_n\left( \phi _0, r\right) \prod ^n_{i=1} G_\mathbb {P}\left( Y - Y'; r, \,\, r_i , b_i \right) \nonumber \\&\quad =\,\sum ^{\infty }_{n=1} \,\left( - \,1\right) ^{n+1} \widetilde{C}_n\left( \phi _0, r\right) \prod ^n_{i=1} G_\mathbb {P}\left( z - z_i\right) . \end{aligned}$$

(26)

$\widetilde{C}_n\left( \phi _0, r\right)$ is shown as the multi-Pomeron amplitudes (pink ovals) in Fig. 14c.

Table 1 Fitted parameters of the model. The values are taken from Ref. [49]

The solution to the non-linear equation is of the following general form:

$$\begin{aligned} N\left( G_\mathbb {P}\left( \phi _0,z\right) \right) = \sum ^{\infty }_{n=1} \,\left( - \,1\right) ^{n+1} C_n\left( \phi _0\right) G_\mathbb {P}^n\left( \phi _0,z\right) . \end{aligned}$$

(27)

Comparing Eq. (26) with Eq. (27) we see

$$\begin{aligned} \widetilde{C}_n\left( \phi _0, r\right) = C_n\left( \phi _0\right) . \end{aligned}$$

(28)

The coefficients $C_n$ can be found from the solution to the Balitsky–Kovchegov equation [72–74] in the saturation region (see Ref. [105]);

$$\begin{aligned} N^\mathrm{BK}\left( G_\mathbb {P}\left( \phi _0,z\right) \right)= & {} a\,\left( 1 - \exp \left( - G_\mathbb {P}\left( \phi _0,z\right) \right) \right) \nonumber \\&+\,\left( 1 - a\right) \frac{ G_\mathbb {P}\left( \phi _0,z\right) }{1 + G_\mathbb {P}\left( \phi _0,z\right) }, \end{aligned}$$

(29)

with a = 0.65. Equation (29) is a convenient parameterization of the numerical solution within accuracy better than 5 %. Having $C_n$ we can calculate the Green function of the dressed BFKL Pomeron using Eq. (25) and the property of the BFKL Pomeron exchange:

$$\begin{aligned}&\frac{\alpha _S^2}{4 \pi } \,\,G_\mathbb {P}\left( Y - 0, r, R; b \right) \nonumber \\&\quad =\int \mathrm{d}^2 r' \mathrm{d}^2 b' \, \mathrm{d}^2 r'' \,\mathrm{d}^2 b'' \,G_\mathbb {P}\left( Y - Y', r, r', \varvec{b} - \varvec{b}^{\,'} \right) \, \, \nonumber \\&\qquad \times \,G_\mathbb {P}\left( Y' r'', R, \varvec{b}^{\,''} \right) \,\,A^\mathrm{BA}_{{\tiny \mathrm{dipole-dipole}}}\left( r', r'', \varvec{b''} - \varvec{b'}\right) .\nonumber \\ \end{aligned}$$

(30)

Carrying out the integrations in Eq. (25), we obtain the Green function of the dressed Pomeron in the following form:

$$\begin{aligned}&G^{{\tiny \mathrm{dressed}}}\left( T\right) = a^2 (1 - \exp \left( -T\right) ) \nonumber \\&\quad +\, 2 a (1 - a)\frac{T}{1 + T} + (1 - a)^2 G\left( T\right) \nonumber \\&\qquad \text{ with }\quad G\left( T\right) = 1 - \frac{1}{T} \exp \left( \frac{1}{T}\right) \Gamma \left( 0, \frac{1}{T}\right) \end{aligned}$$

(31)

where $\Gamma \left( s, z\right)$ is the upper incomplete gamma function (see Ref. [139] formula 8.35) and T is the BFKL Pomeron in the vicinity of the saturation scale

$$\begin{aligned} T\left( r_\bot , s, b\right) = \phi _0 \left( r^2_\bot Q^2_s\left( Y, b\right) \right) ^{\bar{\gamma }} \end{aligned}$$

(32)

3.2 Phenomenological assumptions and phenomenological parameters

The first phenomenological idea, is to fix the large impact parameter behaviour by assuming that the saturation momentum depends on b in the following way:

$$\begin{aligned} Q^2_s\left( b, Y\right) = Q^2_{0s}\left( b, Y_0\right) \,e^{\lambda \,(Y - Y_0)} \end{aligned}$$

(33)

with

$$\begin{aligned}&Q^2_{0s}\left( b, Y_0\right) = \left( m^2\right) ^{1 - 1/\bar{\gamma }}\,\left( S\left( b, m\right) \right) ^{1/\bar{\gamma }} \nonumber \\&S\left( b , m \right) = \frac{m^2}{2 \pi } e^{ - m b}\quad \text{ and }\quad \bar{\gamma }= 0.63. \end{aligned}$$

(34)

We have introduced a new phenomenological parameter m to describe the large b behaviour (see Refs. [47, 48]). The Y dependence as well as $r^2$ dependence, can be found from CGC/saturation approach [31], since $\phi _0$ and $\lambda$ can be calculated in the leading order of perturbative QCD. However, since the higher order corrections turn out to be large [110, 111] we treat them as parameters to be fitted. m is non-perturbative parameter which determines the typical sizes of dipoles inside hadrons. As one can see from Table 1 from the fit $m = 5.25$ GeV, supporting our main assumption that we can apply the BFKL Pomeron calculus, based on perturbative QCD, to the soft interaction since $m \gg \mu _\mathrm{soft}$ where $\mu _\mathrm{soft}$ is the scale of soft interaction, which is of the order of the mass of pion or $\Lambda _\mathrm{QCD}$.

Unfortunately, since the confinement problem is far from being solved, we have to assume a phenomenological approach for the structure of the colliding hadrons. We use a two channel model, which allows us to calculate the diffractive production in the region of small masses. In this model, we replace the rich structure of the diffractively produced states, by a single state with the wave function $\psi _D$, a la Good and Walker [112]. The observed physical hadronic and diffractive states are written in the form

$$\begin{aligned}&\psi _h = \alpha \,\Psi _1+\beta \,\Psi _2;\quad \psi _D = -\beta \,\Psi _1+\alpha \,\Psi _2;\nonumber \\&\text{ where }\quad \alpha ^2+\beta ^2 = 1; \end{aligned}$$

(35)

Functions $\psi _1$ and $\psi _2$ form a complete set of orthogonal functions $\{ \psi _i \}$ which diagonalize the interaction matrix T

$$\begin{aligned} A^{i'k'}_{i,k}=\langle \psi _i\,\psi _k|\mathbf {T}|\psi _{i'}\,\psi _{k'}\rangle = A_{i,k}\,\delta _{i,i'}\,\delta _{k,k'}. \end{aligned}$$

(36)

The unitarity constraints take the form

$$\begin{aligned} 2\,\text{ Im }\,A_{i,k}\left( s,b\right) =|A_{i,k}\left( s,b\right) |^2 +G^{in}_{i,k}(s,b), \end{aligned}$$

(37)

where $G^{in}_{i,k}$ denotes the contribution of all non-diffractive inelastic processes, i.e. it is the summed probability for these final states to be produced in the scattering of a state i off a state k. In Eq. (37) $\sqrt{s}=W$ denotes the energy of the colliding hadrons, and b the impact parameter. A simple solution to Eq. (37) at high energies has the eikonal form with an arbitrary opacity $\Omega _{ik}$, where the real part of the amplitude is much smaller than the imaginary part. We have

$$\begin{aligned}&A_{i,k}(s,b)=i \left( 1 -\exp \left( - \Omega _{i,k}(s,b)\right) \right) ,\end{aligned}$$

(38)

$$\begin{aligned}&G^{in}_{i,k}(s,b)=1-\exp \left( - 2\,\Omega _{i,k}(s,b)\right) . \end{aligned}$$

(39)

Equation (39) implies that $P^S_{i,k}=\exp \left( - 2\,\Omega _{i,k}(s,b) \right)$, is the probability that the initial projectiles (i, k) reach the final state interaction unchanged, regardless of the initial state re-scatterings.

3.3 Small parameters from the fit and the scattering amplitude

The first approach is to use the eikonal approximation for $\Omega$ in which

$$\begin{aligned}&\Omega _{i,k}(r_\bot , Y - Y_0,b) \nonumber \\&\quad = \int \mathrm{d}^2 b'\,\mathrm{d}^2 b''\, g_i\left( \varvec{b}'\right) \,G^{{\tiny \mathrm{dressed}}}\left( T\left( r_\bot , Y - Y_0, \varvec{b}''\right) \right) \nonumber \\&\qquad \times \,g_k\left( \varvec{b} - \varvec{b}'\ - \varvec{b}''\right) \end{aligned}$$

(40)

We propose a more general approach, which takes into account new small parameters, which come from the fit to the experimental data (see Table 1 and Fig. 14 for notations):

$$\begin{aligned} G_{3\mathbb {P}}/g_i(b = 0 ) \ll 1;\quad m\,\gg \, m_1\quad \text{ and }\quad m_2. \end{aligned}$$

(41)

The second equation in Eq. (41) leads to the fact that $b''$ in Eq. (40) is much smaller than b and $b'$, therefore, Eq. (40) can be re-written in a simpler form:

$$\begin{aligned}&\Omega _{i,k}(r_\bot , Y - Y_0, b) = \Bigg (\int \mathrm{d}^2 b''\, G^{{\tiny \mathrm{dressed}}}\left( T\left( r_\bot , Y - Y_0, \varvec{b}''\right) \right) \Bigg ) \nonumber \\&\qquad \times \,\int \mathrm{d}^2 b' g_i\left( \varvec{b}'\right) \,g_k\left( \varvec{b} - \varvec{b}'\right) \,\nonumber \\&\quad =\,\tilde{G}^{{\tiny \mathrm{dressed}}}\left( r_\bot , Y - Y_0\right) \,\, \int \mathrm{d}^2 b' g_i\left( \varvec{b}'\right) \,g_k\left( \varvec{b} - \varvec{b}'\right) \end{aligned}$$

(42)

Using the first small parameter of Eq. (41), we can see that the main contribution stems from the net diagrams shown in Fig. 14b. The sum of these diagrams [49] leads to the following expression for $\Omega _{i,k}(s,b)$:

$$\begin{aligned}&\Omega \left( r_\bot , Y-Y_0; b\right) = \int \mathrm{d}^2 b' \nonumber \\&\quad \times \frac{ g_i\left( \varvec{b}'\right) \,g_k\left( \varvec{b} - \varvec{b}'\right) \,\tilde{G}^{{\tiny \mathrm{dressed}}}\left( r_\bot , Y - Y_0\right) }{1 + G_{3\mathbb {P}}\,\tilde{G}^{{\tiny \mathrm{dressed}}}\left( r_\bot , Y - Y_0\right) \left[ g_i\left( \varvec{b}'\right) + g_k\left( \varvec{b} - \varvec{b}'\right) \right] };\end{aligned}$$

(43)

$$\begin{aligned}&g_i\left( b \right) = g_i \,S_p\left( b; m_i \right) ; \end{aligned}$$

(44)

where

$$\begin{aligned} S_p\left( b,m_i\right) = \frac{1}{4 \pi } m^3_i \,b \,K_1\left( m_i b \right) \end{aligned}$$

(45)

$$\begin{aligned} \tilde{G}^{{\tiny \mathrm{dressed}}}\left( r_\bot , Y -Y_0\right) \!=\! \int \mathrm{d}^2 b \,\,G^{{\tiny \mathrm{dressed}}}\left( T\left( r_\bot , Y \!-\! Y_0, b\right) \right) \nonumber \\ \end{aligned}$$

(46)

where $T\left( r_\bot , Y - Y_0, b\right)$ is given by Eq. (32).

Note that $\tilde{G}^{{\tiny \mathrm{dressed}}}\left( Y - Y_0\right)$ does not depend on b. In all previous formulae, the value of the triple BFKL Pomeron vertex is known: $G_{3 \mathbb {P}} = 1.29\,\mathrm{GeV}^{-1}$.

To simplify further discussion, we introduce the notation

$$\begin{aligned}&N^\mathrm{BK}\left( G^i_\mathbb {P}\left( r_\bot , Y,b \right) \right) = a\,\left( 1 - \exp \left( - G^i_\mathbb {P}\left( r_\bot , Y, b\right) \right) \right) \nonumber \\&\quad +\,\left( 1 - a\right) \frac{ G^i_\mathbb {P}\left( r_\bot , Y, b\right) }{1 + G^i_\mathbb {P}\left( r_\bot , Y, b\right) }, \end{aligned}$$

(47)

with $a = 0.65$. Equation (47) is an analytical approximation to the numerical solution for the BK equation [105]. $G^{i}_\mathbb {P}\left( r_\bot , Y; b\right) = g_i\left( b \right) \,\tilde{G}^{{\tiny \mathrm{dressed}}}\left( r_\bot , Y - Y_0\right)$. We recall that the BK equation sums the ‘fan’ diagrams.

Fig. 15

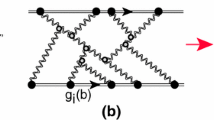
The Mueller diagrams for the BE correlation for the ‘dressed’ Pomeron. A blob denotes the vertex for gluon emission $a_{\mathbb {P}\mathbb {P}}$ (see Eq. (50))

For the elastic amplitude we have

$$\begin{aligned} a_{el}(b) = \left( \alpha ^4 A_{1,1} + 2 \alpha ^2\,\beta ^2\,A_{1,2} + \beta ^4 A_{2,2}\right) . \end{aligned}$$

(48)

We will discuss the inclusive production as well as LRR correlations in Appendix B.

4 Azimuthal angle correlation and the structure of the ‘dressed’ Pomeron

As has been discussed, our model includes three dimensional scales: m, $m_1$ and $m_2$. $m_1$ and $m_2$ describe two typical sizes in the proton wave function, which could be associated with the distance between constituent quarks (size of proton) $R_p \sim 1/m_1$ and the size of the constituent quark $R_q \sim 1/m_2$ in the framework of the constituent quark model [117–123]. The third scale: m, characterizes the impact parameter behaviour of the saturation scale, and is intimately related to the structure of the dressed Pomeron in our model. In Sect. 2 we discussed how two scales in the proton wave function arise in the BE correlations. Here, we would like to show that the third scale leads to the BE correlations which can explain the values of $v_n$ observed experimentally.

As we have discussed in Sect. 3.1, the dressed Pomeron is the sum of enhanced diagrams (see Fig. 14a), which is given by Eq. (31). Therefore, the exchange of the dressed Pomeron generates the production of an infinite number of the parton showers and, in particular, two parton showers which generate the BE correlations as is shown in Fig. 15. Integration over rapidities of triple Pomeron vertices [100] reduces the diagrams of Fig. 15a and b to the diagrams of Fig. 15c and d. We can calculate the probability to find two parton showers ($P_2$) inside of the dressed Pomeron expanding Eq. (31):

$$\begin{aligned} P_2=(2 - 2 a + a^2/3) = 0.91\quad \text{ for }\quad a =0.65 \end{aligned}$$

(49)

and the contribution of two parton showers production to the double inclusive cross section for the diagrams of Fig. 15a, is equal to

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} \nonumber \\&\quad =\,a^2_{\mathbb {P}\mathbb {P}}\,P^2_2 \,\int \mathrm{d}^2 k_T \, \, T\left( k_T, Y- y_1\right) \,T\left( k_T, Y- y_2\right) \, \nonumber \\&\qquad \times T\left( k_T, y_1\right) \,T\left( k_T,\ y_2\right) \end{aligned}$$

(50)

where $a_{\mathbb {P}\mathbb {P}}$ denotes the Mueller vertex of gluon emission (see Fig. 15). In our estimates for the calculation of $v_n$, we do not need to know the probability $P_2$, as well as the vertex $a_{\mathbb {P}\mathbb {P}}$, assuming that $a_{\mathbb {P}\mathbb {P}}$ is the same in Fig. 15a and b. In Eq. (50) all rapidities are in the laboratory frame.

$T\left( k_T, y\right)$ is the Fourier image of $T\left( b, y\right)$ defined in Eqs. (32)–(34) and it takes the form

$$\begin{aligned} T\left( k_T, y \right) = \phi _0\,\frac{1}{\left( 1 + \frac{k^2_T}{m^2}\right) ^{3/2}}\,e^{\lambda \,\bar{\gamma }\left( Y - Y_0\right) }. \end{aligned}$$

(51)

Fig. 16

The Mueller diagrams for the BE correlation for the ‘dressed’ Pomeron for proton–nucleus scattering. Black blob denotes the vertex for gluon emission $a_{\mathbb {P}\mathbb {P}}$ (see Eq. (41), the grey blob stands for the triple Pomeron vertex

Fig. 17

Graphic form of equation for $T_A\left( y, k_T\right)$. The wavy double lines denote $T\left( Y,k_T\right)$ of Eq. (51), while the wavy lines stand for $T_A \left( y, k_T=0\right)$

For the interaction with nuclei, we need to take into account the interaction of the Pomeron with the nucleons inside the nucleus, as shown in Fig. 16. The equation for the resulting $T_A\left( y, k_T\right)$ takes the form (see Fig. 17a)

$$\begin{aligned}&T_A\left( y, k_T\right) = T\left( y, k_T\right) - \Gamma _{3 \mathbb {P}} \nonumber \\&\quad \times \int ^y_0\,\mathrm{d} y'\,T\left( y - y', k_T\right) \nonumber \\&\quad \times \int \mathrm{d}^2 k'_T\, G_A\left( y', \varvec{k} - \varvec{k}'\right) \,T_A\left( y', k'_T \right) . \end{aligned}$$

(52)

The triple Pomeron vertex $\Gamma _{3\mathbb {P}}$ will be calculated in our model below.

The typical $| \varvec{k} - \varvec{k}'| \sim 1/R_A \ll 1/m$ and, therefore, we can replace $G_A( y', \varvec{k} - \varvec{k}')$ by $\widetilde{G}_A( y' ) \delta ^{(2)}( \varvec{k} - \varvec{k}' )$. Note that the normalization is such that the first diagram for $\widetilde{G}_A = S_A( b = 0) T( y,k_T=0)$, where $S_A(b)$ is defined in Eq. (C4). After integration over $k'_T$, Eq. (52) reduces to the following equation:

$$\begin{aligned}&T_A\left( y, k_T\right) = T\left( y, k_T\right) -\Gamma _{3 \mathbb {P}}\nonumber \\&\quad \times \int ^y_0\,\mathrm{d} y'\,T\left( y - y', k_T\right) \widetilde{G}_A\left( y' \right) \,T_A\left( y', k'_T \right) . \end{aligned}$$

(53)

For $\widetilde{G}_A$ we have the equation of Fig. 17b, which has the following analytical form:

$$\begin{aligned}&\widetilde{G}_A\left( y \right) = S_A\left( b=0\right) \,T\left( y, k_T=0 \right) \nonumber \\&\quad -\,\Gamma _{3 \mathbb {P}}\int ^y_0\,\mathrm{d} y'\,\,T \left( y - y', k_T\right) \widetilde{G}^2_A\left( y' \right) \end{aligned}$$

(54)

The solution to these two equations (Eqs. (53) and (54)) can be written as follows:

$$\begin{aligned} T_A\left( y,k_T\right) = \frac{T\left( y,k_T\right) }{1 + \tilde{\Gamma }_{3 \mathbb {P}} \,S_A\left( b=0 \right) \,T\left( y,k_T\right) } \end{aligned}$$

(55)

where $\tilde{\Gamma }_{3 \mathbb {P}} = \Gamma _{3 \mathbb {P}}/\left( \lambda \,\bar{\gamma }\right) = P_2$.

$T\left( y, k_T\right)$ has a physical meaning, of the BFKL amplitude in the vicinity of the saturation scale, where it has a geometric scaling behaviour [124–127], and it depends on one variable $z = \ln \left( r^2 Q^2_s(Y)\right)$. For diagrams of Fig. 15 typically $r \sim 1/m_i$ and $z \rightarrow \lambda Y$. It is well known that the main contribution to the inclusive cross section stems from vicinity of the saturation scale, since this cross section is proportional to $\nabla ^2_r N \left( r, b; Y\right)$, which tends to zero inside the saturation domain (see Eq. (A9)). N is the scattering amplitude of the dipole with size r. The fact that we are dealing with the amplitude in the region where it has geometric scaling behaviour, is the reason why a non-linear equation of the BK type [72–74] is degenerate to one dimensional equations (see Eqs. (53)–(55)).

Using Eq. (50) we can calculate $C( | \varvec{p}_{T1} - \varvec{p}_{T2}|)$ for proton–proton scattering, given by Eq. (1) which is equal to

$$\begin{aligned} C_\mathrm{pp}\left( | \varvec{p}_{T1} - \varvec{p}_{T2}|\right) = \frac{1}{N^2_c - 1} \frac{ \,\int \mathrm{d}^2 k_T \, \, T\left( k_T, Y- y_1\right) \,T\left( k_T, Y- y_2\right) \, T\left( \varvec{k}_T - \varvec{p}_{T,12}, y_1\right) \,T\left( \varvec{k}_T -\varvec{p}_{T,12},\ y_2\right) }{ \,\int \mathrm{d}^2 k_T \, \, T\left( k_T, Y- y_1\right) \,T\left( k_T, Y- y_2\right) \, T\left( k_T, y_1\right) \,T\left( k_T,\ y_2\right) }.\qquad \qquad \quad \end{aligned}$$

(56)

For proton–nucleus scattering we have

$$\begin{aligned} C_\mathrm{pA}\left( | \varvec{p}_{T1} - \varvec{p}_{T2}|\right) = \frac{1}{N^2_c - 1} \frac{ \,\int \mathrm{d}^2 k_T \, \, T_A\left( k_T, Y- y_1\right) \,T_A\left( k_T, Y- y_2\right) \, T\left( \varvec{k}_T -\varvec{p}_{T,12}, y_1\right) \,T\left( \varvec{k}_T -\varvec{p}_{T,12},\ y_2\right) }{ \,\int \mathrm{d}^2 k_T \, \, T\left( k_T, Y- y_1\right) \,T\left( k_T, Y- y_2\right) \, T\left( k_T, y_1\right) \,T\left( k_T,\ y_2\right) }\qquad \qquad \end{aligned}$$

(57)

and for nucleus–nucleus $C_\mathrm{AA}$ has the form

$$\begin{aligned} C_\mathrm{AA}\left( | \varvec{p}_{T1} - \varvec{p}_{T2}|\right) = \frac{1}{N^2_c - 1} \frac{ \,\int \mathrm{d}^2 k_T \, \, T_A\left( k_T, Y- y_1\right) \,T_A\left( k_T, Y- y_2\right) \, T_A\left( \varvec{k}_T -\varvec{p}_{T,12}, y_1\right) \,T_A\left( \varvec{k}_T -\varvec{p}_{T,12},\ y_2\right) }{ \,\int d^2 k_T \, \, T\left( k_T, Y- y_1\right) \,T\left( k_T, Y- y_2\right) \, T\left( k_T, y_1\right) \,T\left( k_T,\ y_2\right) }.\qquad \,\,\, \end{aligned}$$

(58)

The results of calculations for $C\left( R_\mathrm{cor} p_{T,12}\right)$ using Eqs. (56)–(58) are plotted in Fig. 18, One can see that the radius of correlations ($R_\mathrm{cor}^2 =B$) turns out to be very small in comparison with the same radius in Figs. 8 and 10.

From $C( R_\mathrm{cor} p_{T,12})$ we can calculate $v_n$ using Eqs. (11) and (12)-1. However, $C( R_\mathrm{cor} p_{T,12})$ shown in Fig. 18, are calculated for the production of gluon jets, while experimentally $v_n$ are measured for a hadron. Following Refs. [128–130] we explore the local parton–hadron duality(LPHD) suggested in Refs. [131–133].

Fig. 18

$C( | \varvec{p}_{T1} - \varvec{p}_{T2}| = p_{T,12})$, calculated using Eqs. (56)–(58), versus $p_{T,12}$ for three reactions: proton–proton, proton–lead and lead–lead collisions at energy $W = 13\,\mathrm{TeV}$. The long dashed curves correspond to $\exp ({-} B\, p^2_{T,12})$ with $B_\mathrm{pp} =0.035\,\mathrm{GeV}^{-2}$, $B_\mathrm{pA} = 0.027\,\mathrm{Ge}4\mathrm{V}^{-2}$ and $B_\mathrm{AA} = 0.022\,\mathrm{GeV}^{-2}$

Fig. 19

$v_n$ versus $p_T$ at $W = 13\,\mathrm{TeV}$ for proton–proton (a), proton–lead (b) and lead–lead (c) scatterings, using Eqs. (11) and (12)-1

Fig. 20

$v_n$ versus $p_T$ for lead–lead collisions. a and b are taken from Refs. [25] and [13], respectively

In our approach the hadrons originate from the decay of a gluon jet, and their transverse momenta are

$$\begin{aligned} \varvec{p}_\mathrm{hadron,\, T} = z\,\varvec{p}_\mathrm{jet,\,T} + \varvec{p}_\mathrm{intristic,\,T} \end{aligned}$$

(59)

where z is the fraction of energy of the jet, carried by the hadron. $\varvec{p}_\mathrm{intristic,\,T}$ is the transverse momentum of the hadron in the mini-jet that has only longitudinal momentum. From Eq. (59) we find that the average $p_T$ of hadrons is equal to

$$\begin{aligned} \langle p_\mathrm{hadron,\, T}\rangle = \sqrt{z^2\,p^2_\mathrm{jet,\,T} + p^2_\mathrm{intristic,\,T}}. \end{aligned}$$

(60)

In Refs. [128–130] we found that we need to take $z =0.5$ and $p_\mathrm{intristic,\,T} = m_{\pi }$ to describe the inclusive spectra of hadron at the LHC. Using Eq. (60) we recalculate $v_n$ for a gluon jet to $v_n$ for hadrons, as shown in Fig. 19. Comparing with the experimental data [2–25], and Figs. 7b and 12, we see that we describe the proton–proton scattering rather well, while for proton–nucleus scattering we obtain $v_2$ which is smaller by 15–20 %.

The data are given for different multiplicities of the produced particles. As suggested in Ref. [116], we do not expect that the our predictions will depend on these multiplicities. We wish to stress that this is our initial basic approach, and needs to be developed in more detail, to enable us to discuss multiplicity and centrality for the hadron–nucleus and nucleus interactions. We plan to generalize our model for the interactions with nuclei in the near future.

Fig. 21

$v_2$ versus $p_T$ at $W = 13\,\mathrm{TeV}$ for proton–proton (a) and proton–lead (b) for the sum of two contributions: the ‘dressed’ Pomeron structure and the diffractive production, discussed in Sect. 2. The percents indicate the fraction of diffractive production in the Pomeron structure

Fig. 22

The ratio $r_n$ versus $p_T$ at $W = 5\,\mathrm{TeV}$ for proton–lead collisions

Comparing our estimates of Fig. 19c for lead–lead collisions with the experimental data (see Fig. 20), one can see that the value of $v_2$ is half of the experimental value [13, 25]. However, for central events with centrality 5–10 % the measured $v_2$, is very close to our estimates. For centrality 0–5 %, $v_n$ with $n \ge 3$, are in good agreement with the experimental data. A further shortcoming of our present approach, is that it lacks the theoretical basis to predict the centrality dependence of the values of $v_n$. We also intend studying this problem in the near future. The weak energy dependence of $v_n$ stems from the general properties of the two parton shower production (see Fig. 7a for illustration), and it is clearly seen in the experimental data (see Fig. 20b and Ref. [13]). We wish to remind the reader that, for $v_{2n}$, Bose–Einstein correlations give one of the many contributions in the framework of perturbative QCD [56–65, 116], while for $v_n$ with odd n ($v_{2n - 1}$), this mechanism is unique. For this reason, it is important to stress that we are successful in describing the values of $v_{2n - 1}$. In particular, we are successful in reproducing $v_3$ and $v_5$ for centrality 5–10 % (see Fig. 20a and Ref. [25]).

In general the $p_T$ distribution is wider than the experimental one. The LPHD approach and Eq. (60) are very approximate, and we need to use a more advanced jet fragmentation function. Second, we need to add together the two mechanisms: one discussed in this section and one discussed in Sect. 2. We need to include a more advanced fragmentation function, together with more careful accounting of the emission vertex in QCD (see Appendix A). We will consider these in a future publication.

The estimates from our model show that the mechanism that has been discussed in Sect. 2 yields about 10–20 % of the contribution which we now consider. In Fig. 21 one can see how the sum of two mechanism occur in $v_2$. One can see that the sum has a wider $p_T$ distribution and a smaller maximal value. For proton–proton collisions both effects make predictions closer to the experimentally observed values of $v_2$ [21]. Figure 21 shows that the Bose–Einstein correlations in our approach cannot be characterized by one correlation radius. We need to introduce at least two radii: the size of the hadron and the typical size of the BFKL Pomeron, which in our approach is the saturation scale. Hence we confirm the structure of the Bose–Einstein correlation suggested in Refs. [134, 135].

One of the properties that has been violated in the estimates in Sect. 2, was the factorization $r_n = 1$ where

$$\begin{aligned} r_n = \frac{V_{n \Delta }\left( p_{T1}, p_{T2}\right) }{\sqrt{V_{n \Delta }\left( p_{T1}, p_{T1}\right) \,V_{n \Delta }\left( p_{T2}, p_{T2}\right) }} = 1. \end{aligned}$$

(61)

Figure 22 shows that Eq. (61) holds at least for $p_T \le 4\,\mathrm{GeV}$ in accordance with the experimental data (see Refs. [22–25]).

5 Conclusions

In this paper we showed how three different dimensional scales in high energy scattering, arise in the Bose–Einstein correlations that generates $v_n$, for even and odd n. The first two scales are intimately related to the structure of the wave function of the hadron, and have an interpretation in the constituent quark model, as the distance between the constituent quarks and the size of the quark. In a more formal way they characterize the size of the vertex of the BFKL Pomeron interaction with the hadron, and the typical size of the same vertex for the diffraction production, in the region of small mass. We demonstrated that these sizes lead to BE correlations which are large, but narrowly distributed in $p_T$.

The third size is the value of the saturation momentum in the CGC/saturation approach and has been used in the construction of our model for the high energy soft interactions. This size is incorporated in the structure of the ‘dressed’ Pomeron in our model. It turns out that this size leads to values of $v_n$ which are close to the experimental values both for even and odd n, and they are broadly distributed in $p_T$. In proton–proton scattering this mechanism is able to describe the experimental data both for even and odd $v_n$, while for proton–nucleus and nucleus-nucleus collisions we obtain smaller values of $v_2$: 20–30 % smaller for proton–lead scattering, and two times smaller for lead–lead collisions. However, we would like to stress that, for centrality 0–10 %, the structure of the Pomeron gives values of $v_n$ which are very close to the experimentally observed ones.

We would like to emphasize that the main result of this paper is the observation that Bose–Einstein correlations in perturbative QCD, generate $v_n$ for odd values of n ($v_{2n - 1}$), while other mechanisms for the azimuthal angle correlations in the framework of perturbative QCD lead only to $v_n$ with even n (see Refs. [56–65]). The fact that our estimates give $v_{2n-1}$ that are close to the experimental data is encouraging and supports our plan for more precise estimates of the Bose–Einstein correlation, based on a more general basis than our particular model for high energy interactions.

Regarding Ref. [116], in which we calculated the value of $v_2$, in the framework of the density variation mechanism proposed in Ref. [64]. The sources of the azimuthal angle correlations considered in this paper are quite different from the Bose–Einstein correlations and, therefore, one should add this mechanism for $v_2$ estimated in Ref. [116] to the Bose–Einstein correlations discussed in this paper.

All estimates were made in the framework of our model for soft interactions which is based on the CGC/saturation approach, but introduces non-perturbative parameters which describe the wave function of the hadron, and the large impact parameter behaviour of the saturation momentum. We describe in this model the total, elastic and diffractive cross sections as well as the inclusive production and long range rapidity correlations, and therefore we trust that we can rely on the model when discussing the azimuthal angle correlations.

We demonstrated in this paper that BE correlations in the framework of CGC/saturation approach are able to explain a substantial part if not the entire, experimental values of $v_n$ for both even and odd n. Therefore, we believe that it is premature to conclude that the origin of the observed long range rapidity correlations are only due to elliptic flow.

Appendices

Appendix A: BFKL contribution for the interference diagram

In this appendix we derive the BFKL contribution (see Fig. 23) to $\frac{\mathrm{d} \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}}\left( k_T, | \varvec{k_T} + \varvec{p}_{T,12}|\right)$ given by Eq. (14).

The Lipatov vertices $\Gamma _\mu ( q_T,p_{T1})$ and $\Gamma _\mu ( q_{T1}, p_{T2})$ have the form (see Ref. [31] for example):

$$\begin{aligned}&\Gamma _\mu \left( q_T,p_{T1}\right) = \frac{1}{p_{T1}^2}\left( \,q^2_T\, \varvec{p}_{T1} -\varvec{q}_T\,p^2_{T1}\right) ;\nonumber \\&\Gamma _\mu \left( q_{T1},p_{T2}\right) = \frac{1}{p_{T2}^2}\left( \,q^2_{T1}\, \varvec{p}_{T2} -\varvec{q}_{T1}\,p^2_{T2}\right) ; \end{aligned}$$

(A1)

and

$$\begin{aligned}&\Gamma _\mu \left( q_T,p_{T1}\right) \, \Gamma _\mu \left( q_{T1},p_{T2}\right) = \frac{q^2_{T1}\,\left( \varvec{q}_T - \varvec{p}_{T2}\right) ^2}{p^2_{T2}} \nonumber \\&\quad +\,\frac{q^2_{T}\,\left( \varvec{q}_{T1} - \varvec{p}_{T1}\right) ^2}{p^2_{T1}} - k^2_T - p^2_{T,12}\frac{q^2_T\,q^2_{T1}}{p^2_{T1}\,p^2_{T2}} \end{aligned}$$

(A2)

where $\varvec{p}_{T,12} = \varvec{p}_{T1} - \varvec{p}_{T2}$, $\varvec{q}^{\,'}_T = \varvec{q}_T - \varvec{p}_{T1}$, $\varvec{q}^{\,'}_{T1} = \varvec{q}_{T1} - \varvec{p}_{T2}$, and $\varvec{q}_{T1} = \varvec{q}_T - \varvec{k}_T$. Equation (A2) can be re-written as

$$\begin{aligned}&\Gamma _\mu \left( q_T,p_{T1}\right) \, \Gamma _\mu \left( q_{T1},p_{T2}\right) \nonumber \\&\quad = \,\frac{q^2_{T1}\,\left( \varvec{q}^{\,'}_T + \varvec{p}_{T,12}\right) ^2}{p^2_{T2}} + \frac{q^2_{T}\,\left( \varvec{q}^{\,'}_{T1} - \varvec{p}_{T,12}\right) ^2}{p^2_{T1}}\nonumber \\&\qquad -\,k^2_T - p^2_{T,12}\frac{q^2_T\,q^2_{T1}}{p^2_{T1}\,p^2_{T2}} \end{aligned}$$

(A3)

$\phi ^\mathrm{BFKL}$ satisfies the following equation:

$$\begin{aligned}&\frac{\partial \phi ^\mathrm{BFKL}\left( Y; q_T,k_T\right) }{\partial \,Y} \nonumber \\&\quad =\bar{\alpha }_S\,\int \frac{\mathrm{d}^2 q'_T}{\pi }\, K\left( k_T,q'_T\right) \,\phi ^\mathrm{BFKL} \left( Y; q'_T,k_T\right) \end{aligned}$$

(A4)

where

$$\begin{aligned}&K\left( k_T,q'_T\right) \nonumber \\&\quad =\left( \frac{q^2_{T1}\,q'^2_T}{p^2_{T}} + \frac{q^2_{T}\,q'^2_{T1}}{p^2_{T}} - k^2_T\right) \frac{1}{q'^2_T\, q'^2_{T1}}\, \nonumber \\&\qquad -\,\left\{ q^2_T \int \frac{\mathrm{d}^2 p_T}{p^2_T\,\left( \varvec{q}_T - \varvec{p}_T\right) ^2} + q'^2_T \int \frac{\mathrm{d}^2 p_T}{p^2_T\,\left( \varvec{q}^{\,'}_T - \varvec{p}_T\right) ^2} \right\} \nonumber \\&\qquad \times \, \delta ^{(2)}\left( \varvec{q}^{\,'}_t - \varvec{q}_T\right) . \end{aligned}$$

(A5)

Equation (A4) is the BFKL equation in the momentum representation, which has the following form in the coordinate representation [39, 40, 70, 71]:

$$\begin{aligned}&\frac{\partial N^\mathrm{BFKL}\left( Y; x_{12}, b\right) }{\partial \,Y} \nonumber \\&\quad =\bar{\alpha }_S\,\int \frac{\mathrm{d}^2 x_3}{\pi }\,\frac{x^2_{12}}{x^2_{13}\,x^2_{23}}\bigg \{N\left( Y; x_{13}, \varvec{b} - \frac{1}{2}{x}_{23}\right) \,\nonumber \\&\qquad +\,N\left( Y; x_{23}, \varvec{b} - \frac{1}{2}{x}_{13}\right) - N\left( Y; x_{13}, b\right) \bigg \} \end{aligned}$$

(A6)

where [31, 113]

$$\begin{aligned}&\frac{1}{\left( \varvec{q}_T + \frac{1}{2}\varvec{k}_T\right) ^2\,\left( \frac{1}{2}\varvec{k}_T - \varvec{q}_T\right) ^2}\phi ^\mathrm{BFKL}\left( q_T,k_T\right) \nonumber \\&\quad =\,\frac{2\,C_F}{\bar{\alpha }_S(2 \pi )^3}\int \mathrm{d}^2 b\,\mathrm{d}^2 x_{12}\,e^{i \varvec{q}_T \cdot \varvec{x}_{12} + i \varvec{k}_T \cdot \varvec{b}} \, N^\mathrm{BFKL}\left( Y; x_{12}, b\right) \nonumber \\ \end{aligned}$$

(A7)

For diagrams Fig. 2c and d $\varvec{p}_{12} = 0$ and plugging Eq. (A7) into Eq. (14) we obtain that

$$\begin{aligned}&\frac{\mathrm{d} \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}}\left( k_T, k_T \right) = \left( \frac{2\, C_F}{\bar{\alpha }_S(2 \pi )^3}\right) ^2\nonumber \\&\quad \times \int \mathrm{d}^2 x_{12} \,\mathrm{d}^2 b\,\mathrm{d}^2 b'\, e^{i \varvec{p}_{T1}\cdot \varvec{x}_{12} + i \varvec{k}_T \cdot \varvec{b}} \nonumber \\&\quad \times \bigg \{ \frac{1}{p_{T1}^2}\left( \left( \left( \frac{1}{2}\varvec{\nabla }_b + \varvec{\nabla }_{x_{12}}\right) ^2 N^\mathrm{BFKL}\left( Y - y; x_{12}, \varvec{b} - \varvec{b}'\right) \right) \,\right. \nonumber \\&\quad \times \left. \left( \left( \frac{1}{2}\varvec{\nabla }_{b'} -\varvec{\nabla }_{x_{12}}\right) ^2\,N^\mathrm{BFKL}\left( y; x_{12}, \varvec{b}'\right) \right) \,\right. \nonumber \\&\quad \left. +\,\left( \left( \frac{1}{2}\varvec{\nabla }_b -\varvec{\nabla }_{x_{12}}\right) ^2 N^\mathrm{BFKL}\left( Y - y; x_{12}, \varvec{b} - \varvec{b}'\right) \right) \,\right. \nonumber \\&\quad \times \left. \left( \left( \frac{1}{2}\varvec{\nabla }_{b'} + \varvec{\nabla }_{x_{12}}\right) ^2\,N^\mathrm{BFKL}\left( y; x_{12}, \varvec{b}'\right) \right) \right) \nonumber \\&\quad -\,\left( \varvec{\nabla }_b N^\mathrm{BFKL}\left( Y - y; x_{12}, \varvec{b} - \varvec{b}' \right) \right) \nonumber \\&\quad \times \left( \varvec{\nabla }_{b'}N^\mathrm{BFKL}\left( y; x_{12}, \varvec{b}'\right) \right) \bigg \}. \end{aligned}$$

(A8)

Equation (A8) in the limit $k_T \rightarrow 0$ degenerates to the expression for the inclusive cross section which has the elegant form derived in Ref. [113],

$$\begin{aligned}&\frac{\mathrm{d} \sigma }{\mathrm{d} y_1 \mathrm{d}^2 p_{T1}}\left( k_T=0, k_T=0 \right) =\left( \frac{2\,C_F}{\bar{\alpha }_S(2 \pi )^3}\right) ^2 \frac{1}{p^2_{T1}}\, \nonumber \\&\qquad \times \int \mathrm{d}^2 x_{12}\,e^{i \varvec{p}_{T1} \cdot x_{12}}\left( \nabla ^2_{x_{12}}\int \mathrm{d}^2 b\, N^\mathrm{BFKL}\left( Y - y; x_{12}, \varvec{b}\right) \right) \,\nonumber \\&\qquad \times \left( \nabla ^2_{x_{12}}\int \mathrm{d}^2 b'\, N^\mathrm{BFKL}\left( y; x_{12}, \varvec{b}'\right) \right) . \end{aligned}$$

(A9)

The interesting feature of Eqs. (A8) and (A9) is that they remain correct, if we replace $2 N^\mathrm{BFKL}$ by $N_G = 2\, N - N^2$, where N is the solution of the Balitsky–Kovchegov equation [72–74]. Inside the saturation domain where $N \rightarrow 1$, both equations lead to negligible contributions. In other words, in both equations the main contributions stem from the vicinity of the saturation scale, where $x^2_{12}\,Q^2_s \approx 1$.

The solution for the scattering amplitude of two dipoles $r_1$ and $r_2$ to Eq. (A6) is well known [39, 40]

$$\begin{aligned}&N_\mathbb {P}\left( r_1,r_2; Y, b \right) \nonumber \\&\quad =\sum _{n=0}^{\infty } \int \frac{\mathrm{d} \gamma }{2\,\pi \,i}\,\phi ^{(n)}_{in}(\gamma ; r_2) \,\,\mathrm{d}^2\, R_1 \,\,\mathrm{d}^2\,R_2 \nonumber \\&\qquad \times \delta (\varvec{R}_1 - \varvec{R}_2 - \varvec{b})\, e^{\omega (\gamma , n )\,Y} \,E^{\gamma ,n}\left( r_1, R_1\right) \,E^{1 - \gamma ,n}\left( r_2, R_2 \right) \nonumber \\ \end{aligned}$$

(A10)

where the functions $\phi ^{(n)}_{in}(\gamma ; r_2)$ are determined by the initial conditions at low energies and

$$\begin{aligned}&\omega (\gamma , n) = \bar{\alpha }_S\chi (\gamma , n) \nonumber \\&\quad =\bar{\alpha }_S\left( 2 \psi \left( 1 \right) - \psi \left( \gamma + |n|/2\right) -\psi \left( 1 - \gamma + |n|/2\right) \right) \nonumber \\ \end{aligned}$$

(A11)

where $\psi \left( \gamma \right) = d \ln \Gamma \left( \gamma \right) /\mathrm{d} \gamma$ and $\Gamma \left( \gamma \right)$ is Euler gamma function. Functions $E^{n, \gamma } \left( \rho _{1a},\rho _{2a}\right)$ are given by the following equations:

$$\begin{aligned} E^{n, \gamma } \left( \rho _{1a},\rho _{2a}\right) = \left( \frac{\rho _{12}}{\rho _{1a} \, \rho _{2a}}\right) ^{1 - \gamma + n/2} \, \left( \frac{\rho ^*_{12}}{\rho ^*_{1a} \, \rho ^*_{2a}} \right) ^{1 - \gamma - n/2}. \end{aligned}$$

(A12)

In Eq. (A12) we use complex numbers to characterize the point on the plane

$$\begin{aligned} \rho _i = x_{i,1} + i \, x_{i,2};\quad \rho ^*_i = x_{i,1} - i \, x_{i,2} \end{aligned}$$

(A13)

where the indices 1 and 2 denote two transverse axes. Note that

$$\begin{aligned}&\rho _{12}\,\rho ^*_{12} = r^2_i;\quad \rho _{1 a}\,\rho ^*_{1 a} = \left( \varvec{R}_i -\frac{1}{2}\varvec{r}_{i}\right) ^2 \nonumber \\&\rho _{2 a}\,\rho ^*_{2a} =\left( \varvec{R}_i + \frac{1}{2}\varvec{r}_{i}\right) ^2. \end{aligned}$$

(A14)

At large values of Y, the main contribution stems from the first term with $n =0$. For this term, Eq. (A12) can be re-written in the form

$$\begin{aligned} E^{\gamma ,0}\left( r_i,R_i\right) = \left( \,\frac{r^2_{i}}{(\varvec{R}_i + \frac{1}{2}\varvec{r}_{i})^2\,\, (\varvec{R}_i - \frac{1}{2}\varvec{r}_{i})^2}\,\right) ^{1 - \gamma }. \end{aligned}$$

(A15)

The integrals over $R_1$ and $R_2$ were taken in Refs. [39, 40, 136–138] and at $n=0$ we have

$$\begin{aligned}&H^\gamma \left( w, w^*\right) \equiv \int \mathrm{d}^2\,R_1\,E^{\gamma ,0}\left( r_{1},R_1\right) \, E^{1 - \gamma , 0}\left( r_{2}, \varvec{R}_1 -\varvec{b}\right) \nonumber \\&\quad = \frac{ (\gamma - \frac{1}{2})^2}{( \gamma (1 - \gamma ) )^2} \bigg \{b_\gamma \,w^\gamma \,{w^*}^\gamma \,F\left( \gamma , \gamma , 2\gamma , w\right) \, F\left( \gamma , \gamma , 2\gamma , w^*\right) \nonumber \\&\qquad + b_{1 - \gamma } w^{1 - \gamma }{w^*}^{1-\gamma } \nonumber \\&F\left( 1 - \gamma , 1 -\gamma , 2 - 2\gamma , w\right) \,F\left( 1 - \gamma ,1 -\gamma ,2 -2\gamma , w^*\right) \bigg \}\nonumber \\&\quad \xrightarrow {b\,\gg \, r_1\, \text{ and/or } \,r_2}\,\,\frac{ (\gamma - \frac{1}{2})^2}{( \gamma (1 - \gamma ) )^2} \nonumber \\&\quad \bigg \{b_\gamma \,w^\gamma \,{w^*}^\gamma + b_{1 - \gamma } w^{1 - \gamma }{w^*}^{1-\gamma }\bigg \}\, \nonumber \\&\quad =\,\frac{ (\gamma - \frac{1}{2})^2}{( \gamma (1 - \gamma ) )^2} \bigg \{b_\gamma \,\left( \frac{r^2_1\,r^2_2}{b^4}\right) ^\gamma + b_{1 - \gamma } \left( \frac{r^2_1\,r^2_2}{b^4}\right) ^{1- \gamma }\bigg \}\nonumber \\ \end{aligned}$$

(A16)

Fig. 23

The graphical representation of Eq. (14)

where F is the hypergeometric function [139]. In Eq. (A16) $w\,w^*$ and $b_{\gamma }$ are equal,

$$\begin{aligned}&w\,w^* = \frac{r^2_{1}\,r^2_{2}}{\left( \varvec{b} - \frac{1}{2}\left( \,\varvec{r}_{1} - \varvec{r}_{2}\right) \right) ^2 \,\left( \varvec{b} + \frac{1}{2}\left( \,\varvec{r}_{1} - \varvec{r}_{2}\right) \right) ^2}; \nonumber \\&b_{\gamma } = \pi ^3 \, 2^{4(1/2 - \gamma )} \, \frac{\Gamma \left( \gamma \right) }{ \Gamma \left( 1/2 - \gamma \right) } \, \frac{\Gamma \left( 1 - \gamma \right) }{\Gamma \left( 1/2 + \gamma \right) }. \end{aligned}$$

(A17)

Therefore, at large b, $N^\mathrm{BFKL}$ decreases as a power of b, which violates the Froissart theorem [28]. At present, as has been mentioned above, we cannot suggest a modification of the equation of the CGC/saturation approach in which the correct [45, 46] exponential behaviour at large b would be incorporated. So we doomed to build a model. We discussed our model in Sect. 3 (Fig. 23).

1.1 Born diagrams

The spirited discussions with our colleagues showed us that it would be beneficial to add a general discussion of the BFKL contribution, by calculating of the first Born diagrams for the production of two identical gluons that have rapidities $y_1$ and $y_2$, and carry momenta $\varvec{p}_{T1}$ and $\varvec{p}_{T2}$. These diagrams are shown in Fig. 24 for the scattering of the bound states of two oniums (two dipoles). Such a model for the scattering systems allows us to use the perturbative QCD approach, and has the analogy in the simplest bound system: deuteron.

Fig. 24

The Born interference diagram for production of two identical gluons with rapidities: $y_1$ and $y_2$ and transverse momenta $\varvec{p}_{T1}$ and $\varvec{p}_{T2}$. $\varvec{R}_i = \frac{1}{2}( \varvec{x}_i +\varvec{y}_i)$, $\varvec{p}_{T,12} = \varvec{p}_{T1} - \varvec{p}_{T2}$. Red rectangle shows function $\Phi ( \varvec{k}, \varvec{p}_{T1},\varvec{p}_{T2})$ (see text)

The two onium bound state is described by the wave function $\Psi \left( \varvec{R}_1 - \varvec{R}_2\right)$, where $R_i$ is the coordinate of the onium which is equal $\varvec{R}_i = \frac{1}{2}( \varvec{x}_i +\varvec{y}_i)$ where $\varvec{x}_i$ and $\varvec{y}_i$ are coordinates of quark and antiquark in the onium (see Fig. 24). We introduce two new functions that describe the form factor of our bound state ($G\left( q \right)$), and the interaction of two gluons with the onium:

$$\begin{aligned}&G\left( q\right) = \int \mathrm{d}^2 R \,|\Psi \left( R\right) |^2\, \,e^{i\,\varvec{q} \cdot \varvec{R}}\quad \text{ with }\quad \varvec{R} = \varvec{R}_1 - \varvec{R}_2;\nonumber \\&\phi _\mathrm{onium}\left( q, k\right) = 2\,\int \mathrm{d}^2 r_i \,|\psi _\mathrm{onium}\left( r_i \right) |^2\,\,e^{i\,\frac{1}{2}\varvec{k}\cdot \varvec{r}_i} \left( 1 + e^{i \varvec{q}\cdot \varvec{r}_i}\right) \nonumber \\&\quad \text{ with }\quad \varvec{r}_i = \varvec{x}_i - \varvec{y}_i. \end{aligned}$$

(A18)

The contribution of the diagram of Fig. 24 can be written as²

$$\begin{aligned} \sigma _\mathrm{interference} \propto \int \frac{\mathrm{d}^2 k}{4 \pi ^2}\,G\left( k\right) \,G\left( \varvec{k} + \varvec{p}_{T,12}\right) \,I^2\left( \varvec{k},\varvec{p}_{T1},\varvec{p}_{T2} \right) \nonumber \\ \end{aligned}$$

(A19)

where

$$\begin{aligned}&I\left( \varvec{k},\varvec{p}_{T1},\varvec{p}_{T2}\right) \propto \int \frac{\mathrm{d}^2 q}{4\, \pi ^2}\,\,\phi _\mathrm{onium}\left( \varvec{k},\varvec{q}\right) \,\phi _\mathrm{onium} \nonumber \\&\quad \times \left( \varvec{k} - \varvec{p}_{T,12},\varvec{q}\right) \nonumber \\&\quad \times \bigg \{\frac{1}{q^2\,\left( \varvec{k} - \varvec{q}\right) ^2} \, \Gamma _\mu \left( q_T, p_{T1}\right) \, \Gamma _\mu \left( q_{T1}, p_{T2}\right) \nonumber \\&\quad \times \frac{1}{\left( \varvec{q} - \varvec{p}_{T1}\right) ^2\,\left( \varvec{k} - \varvec{p}_{T,12} - \varvec{q}\right) ^2}\bigg \} \end{aligned}$$

(A20)

where $\Gamma _\mu \left( q_T, p_{T1}\right) \, \Gamma _\mu \left( q_{T1}, p_{T2}\right)$ is given by Eqs. (A2) and (A3).

One can see from Eqs. (A19) and (3) that the typical $q \approx 1/r$, where r is he size of the onium, while the typical values of $k \propto 1/R$, where R is the size of the bound state. Assuming that $R \gg r$, we see that $k \ll q$. Anticipating $p_{T,12} \propto 1/R$, we can reduce the contribution of the interference diagram to the following form:

$$\begin{aligned}&\sigma _\mathrm{interference} \propto \frac{1}{p^2_{T1} \,p^2_{T,2}}\int \frac{\mathrm{d}^2 k}{4 \pi ^2}\,G\left( k\right) \,G\left( \varvec{k} + \varvec{p}_{T,12}\right) \nonumber \\&\quad \times \bigg (\int \frac{\mathrm{d}^2 q}{4 \pi ^2}\frac{1}{q^2\,\left( \varvec{q} - \varvec{p}_{T1}\right) ^2}\bigg )^2. \end{aligned}$$

(A21)

In Eq. (A21) we assume that $p_{T1} \approx p_{T2}$ and one can see that $p_{T,12}$ from this equation is indeed of the order of 1 / R, being much smaller than $p_{Ti}$ if they are of the order of 1 / r. For $1/R \ll p_{Ti} \ll 1/r$ we need to take $\Gamma _\mu \left( q_T, p_{T1}\right) \, \Gamma _\mu \left( q_{T1}, p_{T2}\right) = \big ( \frac{1}{p^2_{T1}} + \frac{1}{p^2_{T2}}\big )\, \frac{1}{q^4}$.

Appendix B: BE correlations in the model: diffractive production in the small mass region

a. Inclusive production

The inclusive production in the framework of the CGC/saturation approach comprises two stages: the gluon mini-jet productions and the decay of this mini-jet into hadrons. For mini-jet production, we use the $k_T$ factorization formula, which has been proven in Ref. [113] in the framework of the CGC/saturation approach (see the appendix for details).

$$\begin{aligned}&\frac{\mathrm{d} \sigma }{\mathrm{d} y \,\mathrm{d}^2 p_T} \nonumber \\&\quad =\frac{2 \pi \bar{\alpha }_S}{C_F}\frac{1}{p^2_T}\,\int \mathrm{d}^2 k_{T}\,\,\phi ^{h_1}_G\left( x_1;\varvec{k}_T\right) \,\phi ^{h_2}_G\left( x_2; \varvec{p}_T -\varvec{k}_T\right) \nonumber \\ \end{aligned}$$

(B1)

where $\phi ^{h_i}_G$ denotes the probability to find a gluon that carries the fraction $x_i$ of energy with $k_T$ transverse momentum, and $\bar{\alpha }_S= \alpha _SN_c/\pi$, with the number of colours equal to $N_c$. $\frac{1}{2}Y + y = \ln (1/x_1)$ and $\frac{1}{2}Y - y =\ln (1/x_2)$. $\phi ^{h_i}_G$ is the solution of the Balitsky–Kovchegov (BK) [72–74] non-linear evolution equation, and can be viewed as the sum of ‘fan’ diagrams of the BFKL Pomeron interactions, shown in Fig. 25.

Fig. 25

The graphic representation of Eq. (B1) (see a). For the sake of simplicity all other indices in $\phi \left( x_1,p_T - k_T\right)$ and $\phi \left( x_2,k_T\right)$ are omitted. The wavy lines denote the BFKL Pomerons, while the helical lines illustrate the gluons. In b the Mueller diagram for inclusive production is shown

In our model the sum of ‘fan’ diagrams is given by Eq. (29). Assuming that the main contribution to

$$\begin{aligned} \frac{\mathrm{d} \sigma }{\mathrm{d} y } = \int \mathrm{d}^2 p_T\,\frac{\mathrm{d} \sigma }{\mathrm{d} y \,\mathrm{d}^2 p_T} \end{aligned}$$

stems from $p_T \le Q_s$, we obtain the following formula:

$$\begin{aligned}&\frac{\mathrm{d} \sigma }{\mathrm{d} y} = \int \mathrm{d}^2 p_T\,\frac{\mathrm{d} \sigma }{\mathrm{d} y \,\mathrm{d}^2 p_T} = a_{\mathbb {P}\mathbb {P}}\,\ln \left( W/W_0\right) \nonumber \\&\quad \times \bigg ( \alpha ^2 \,\mathrm{In}^{(1)}\left( \frac{1}{2}Y + y\right) + \beta ^2 \, \mathrm{In}^{(2)}\left( \frac{1}{2}Y + y\right) \bigg )\nonumber \\&\quad \times \bigg ( \alpha ^2 \,\mathrm{In}^{(1)}\left( \frac{1}{2}Y - y\right) +\beta ^2 \, In^{(2)}\left( \frac{1}{2}Y - y\right) \bigg ) \end{aligned}$$

(B2)

where

$$\begin{aligned}&\mathrm{In}^{(i)}\left( y\right) = \int \mathrm{d}^2 b \,\,N^\mathrm{BK}\left( g^{(i)}\,S\left( m_i, b\right) \,\tilde{G}_\mathbb {P}\left( y\right) \right) \quad \text{ or } \nonumber \\&\mathrm{In}^{(i)}\left( y \right) = I^\mathrm{BK}_i\left( y, Q_T=0\right) ;\quad \text{ with }\quad I^\mathrm{BK}_i\left( y, Q_T\right) \nonumber \\&\quad =\,\int \mathrm{d}^2 b \,e^{i \varvec{b} \cdot \varvec{Q}_T}\,\,N^\mathrm{BK}\left( g^{(i)}\,S\left( m_i, b\right) \,\tilde{G}_\mathbb {P}\left( y\right) \right) \end{aligned}$$

(B3)

where $\tilde{G}_\mathbb {P}\left( y\right)$ and $N^\mathrm{BK}$ have been defined in Eq. (46) and in Eq. (29), respectively. Regarding the factor in front of Eq. (B2) i.e. $\ln \left( W/W_0\right)$, where $W = \sqrt{s}$ is the energy of collision in c.m. frame, and $W_0$ is the value of energy from which we start our approach. One can see that Eq. (B1) is divergent in the region of small $p_T < Q_s$. Indeed, in this region $\phi$’s in Eq. (B1) do not depend on $p_T$, since $k_T \approx Q_s > p_T$, and the integration over $p_T$ leads to $\ln ( Q^2_s/m^2_\mathrm{soft})$, where $m_\mathrm{soft}$ is the non-perturbative scale, that includes the confinement of quarks and gluons ($m_\mathrm{soft} \sim \Lambda _\mathrm{QCD})$.

Fig. 26

The Mueller diagram for the rapidity correlation between two particles produced in two parton showers. a The first Mueller diagram, while b indicates the structure of general diagrams. The double wavy lines describe the dressed BFKL Pomerons. The blobs stand for the vertices as shown in the legend

1.1 b. LRR correlations

In Ref. [52], we showed that in the framework of our model that has been described above, the main source of the long range rapidity correlation, is the correlation between two parton showers. In other words, it was shown that the contribution to the correlation function from enhanced and semi-enhanced diagrams, turns out to be negligibly small.

The appropriate Mueller diagrams are shown in Fig. 26. Examining this diagram, we see that the contribution to the double inclusive cross section, differs from the product of two single inclusive cross sections. This difference generates the rapidity correlation function, which is defined as

$$\begin{aligned} R\left( y_1, y_2\right) = \frac{\frac{1}{\sigma _{in}} \frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1\,\mathrm{d} y_2}}{\frac{1}{\sigma _{in}} \frac{\mathrm{d} \sigma }{\mathrm{d} y_1} \, \frac{1}{\sigma _{in}} \frac{\mathrm{d} \sigma }{\mathrm{d} y_2} } - 1. \end{aligned}$$

(B4)

There are two reasons for the difference between the double inclusive cross section due to production of two parton showers, and the products of inclusive cross sections: the first, is that in the expression for the double inclusive cross section, we integrate the product of the single inclusive cross sections, over b or $Q_T$(see Fig. 25a and Eq. (13)). The second, is that the summation over i and k for the product of single inclusive cross sections, is for fixed i and k (see Fig. 25a).

Introducing the following new function enables us to write the analytical expression for the double inclusive cross section:

$$\begin{aligned}&I^{(i,k)}\left( y, b \right) = \tilde{a}_{\mathbb {P}\mathbb {P}} \,\int \mathrm{d}^2 b' \,\,N^\mathrm{BK} \bigg ( g^{(i)}\,S\left( m_i,b'\right) \nonumber \\&\quad \times \, \tilde{G}^{{\tiny \mathrm{dressed}}}\left( r_\bot = 1/m, \frac{1}{2}Y + y \right) \bigg )\,\nonumber \\&\quad \times \, N^\mathrm{BK}\bigg ( g^{(k)}\,S\left( m_k, \varvec{b} - \varvec{b}^{\,'}\right) \tilde{G}^{{\tiny \mathrm{dressed}}}\left( r_\bot =1/m,\frac{1}{2}Y- y \right) \bigg )\nonumber \\ \end{aligned}$$

(B5)

where $\tilde{a}_{\mathbb {P}\mathbb {P}} = a_{\mathbb {P}\mathbb {P}} \,\ln \left( W/W_0\right)$.

Using Eq. (B5) we can write the double inclusive cross section in two equivalent forms

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{{\tiny }\mathrm{2 parton\, showers}}}{ \mathrm{d} y_1\,\,\mathrm{d} y_2} = \int \mathrm{d}^2p_{1T}\,\mathrm{d}^2 p_{2T}\frac{\mathrm{d}^2 \sigma ^{{\tiny } \mathrm{2 parton\, showers}}}{ \mathrm{d} y_1\,\,\mathrm{d} y_2\,\mathrm{d}^2 p_{1T}\,\mathrm{d}^2 p_{2T}} \nonumber \\&\quad =\,\int \mathrm{d}^2 b \,\,\bigg \{ \alpha ^4 \,I^{(1,1)}\left( y_1, b \right) \,I^{(1,1)}\left( y_2, b \right) + \alpha ^2\,\beta ^2\, \nonumber \\&\qquad \times \left( I^{(1,2)}\left( y_1, b \right) \,I^{(1,2)}\left( y_2, b \right) +,I^{(2,1)}\left( y_1, b \right) \,I^{(2,1)}\left( y_2, b \right) \right) \nonumber \\&\qquad +\,\beta ^4\,I^{(2,2)}\left( y_1, b \right) \,I^{(2,2)}\left( y_2, b \right) \bigg \} \end{aligned}$$

(B6)

$$\begin{aligned}&\quad =\frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{p^2_{T1}\,p^2_{T2}}\, \nonumber \\&\qquad \times \int \mathrm{d}^2 Q_T \bigg ( \alpha ^2 I^\mathrm{BK}_1\left( \frac{1}{2}Y +y_1; Q_T\right) I^\mathrm{BK}_1\left( \frac{1}{2}Y +y_2; Q_T\right) \,\nonumber \\&\qquad +\,\beta ^2\, I^\mathrm{BK}_2\left( \frac{1}{2}Y +y_1; Q_T\right) I^\mathrm{BK}_2\left( \frac{1}{2}Y +y_2; Q_T\right) \bigg ) \nonumber \\&\qquad \times \, \bigg ( \alpha ^2 I^\mathrm{BK}_1\left( \frac{1}{2}Y -y_1; Q_T\right) I^\mathrm{BK}_1\left( \frac{1}{2}Y -y_2; Q_T\right) \,\nonumber \\&\qquad +\, \beta ^2\, I^\mathrm{BK}_2\left( \frac{1}{2}Y -y_1; Q_T\right) I^\mathrm{BK}_2\left( \frac{1}{2}Y -y_2; Q_T\right) \bigg ) \,\nonumber \\&\quad \equiv \frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{p^2_{T1}\,p^2_{T2}} \nonumber \\&\qquad \times \,\int \mathrm{d}^2 Q_T \,F^\mathrm{BK}_{12}\left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; Q_T\right) \nonumber \\&\qquad \times F^\mathrm{BK}_{12}\left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2; Q_T\right) \end{aligned}$$

(B7)

where $F^\mathrm{BK}_{12}$ is equal to

$$\begin{aligned}&F^\mathrm{BK}_{12}\left( Y_1, Y_2; Q_T\right) = \alpha ^2 I^\mathrm{BK}_1\left( Y_1; Q_T\right) I^\mathrm{BK}_1\left( Y_2; Q_T\right) \,\nonumber \\&\quad +\, \beta ^2\, I^\mathrm{BK}_2\left( Y_1; Q_T\right) I^\mathrm{BK}_2\left( Y_2; Q_T\right) \end{aligned}$$

(B8)

Recall that all rapidities are in the c.m. frame.

1.1.1 c. $v_n$ for proton–proton collisions

Using Eq. (B7), Eq. (10) can be re-written in the following form:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} = \frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{p^2_{T1}\,p^2_{T2}}\,\nonumber \\&\quad \times \int \mathrm{d}^2 k_T \, F^\mathrm{BK}_{12}\left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; k_T\right) \,\nonumber \\&\quad \times F^\mathrm{BK}_{12}\left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2; k_T\right) \nonumber \\&\quad +\,\frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{N^2_c - 1}\,\frac{1}{4}\left( \frac{1}{p^2_{T1}} + \frac{1}{p^2_{T2}}\right) ^2 \nonumber \\&\quad \times \int \mathrm{d}^2 k_T \,F^\mathrm{BK}_{12}\left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; \varvec{k}_T \right) \,\nonumber \\&\quad \times \,F^\mathrm{BK}_{12}\left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2;\varvec{k}_T + \varvec{p}_{T,12} \right) . \end{aligned}$$

(B9)

In Eq. (B9) we neglected the contribution $\propto p^2_{T,12}$ in the vertex of gluon emission in Fig. 23 (see Appendix A1), as well as the dependence of the BFKL Pomeron on the momentum transfer. The small size of both quantities stem from the fact that in our model, $k_T$ dependence in Eq. (B9) is determined by the proton structure and the typical $k_T \sim m_1 \mathrm{}$ or $m_2$ (see Table 1), while typical transverse momentum in the BFKL Pomeron is about $Q_s$ or m, and it is much larger than $m_1$ or $m_2$.

Appendix C: Hadron–nucleus interaction in the model

In the case of the hadron–nucleus interaction the general formula of Eq. (B7) can be re-written in the form [114]

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma ^{{\tiny } \mathrm{2 parton\, showers}}}{ \mathrm{d} y_1\,\mathrm{d} y_2} = \int \mathrm{d}^2p_{1T}\,\mathrm{d}^2 p_{2T}\frac{\mathrm{d}^2 \sigma ^{{\tiny }\mathrm{2 parton\, showers}}}{ \mathrm{d} y_1\,\,\mathrm{d} y_2\,\mathrm{d}^2 p_{1T}\,\mathrm{d}^2 p_{2T}} \end{aligned}$$

(C1)

$$\begin{aligned}&\quad =\frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{p^2_{T1}\,p^2_{T2}}\, \int \mathrm{d}^2 Q_T \nonumber \\&\qquad \times \bigg ( \alpha ^2 I^\mathrm{BK}_1\left( \frac{1}{2}Y +y_1; Q_T\right) I^\mathrm{BK}_1\left( \frac{1}{2}Y +y_2; Q_T\right) + \beta ^2\, \nonumber \\&\qquad \times I^\mathrm{BK}_2\left( \frac{1}{2}Y +y_1; Q_T\right) I^\mathrm{BK}_2\left( \frac{1}{2}Y +y_2; Q_T\right) \bigg ) \nonumber \\&\qquad \times \, I^\mathrm{BK}_A\left( \frac{1}{2}Y -y_1; Q_T\right) \,I^\mathrm{BK}_A\left( \frac{1}{2}Y -y_2; Q_T\right) \ \,\nonumber \\&\quad \equiv \frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{p^2_{T1}\,p^2_{T2}}\, \int \mathrm{d}^2 Q_T \,F^\mathrm{BK}_{12}\left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; Q_T\right) \, \nonumber \\&\qquad \times F^\mathrm{BK}_{A}\left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2; Q_T\right) \end{aligned}$$

(C2)

where

$$\begin{aligned}&I^\mathrm{BK}_A\left( y,Q_T\right) = \int \mathrm{d}^2 b e^{i \varvec{b} \cdot \varvec{Q}_T} \,N^\mathrm{BK} \nonumber \\&\quad \times \left( \left( \alpha ^2 In^{(1)}\left( y\right) + \beta ^2\,In^{(2)}\left( y\right) \right) S_A\left( b \right) \right) \end{aligned}$$

(C3)

where $\mathrm{In}^{(i)}$ are defined in Eq. (B3) and $S_A\left( b \right)$ is the nucleus Wood–Saxon distribution [115] given by

$$\begin{aligned}&S_A\left( b \right) = \int ^\infty _{- \infty } \mathrm{d} z \,\frac{\rho _0}{1 + \exp \bigg ( \frac{\sqrt{z^2 + b^2} - R_A}{h}\bigg )}\nonumber \\&\quad \text{ where }\quad \int \mathrm{d}^2 b \,S_A\left( b \right) = A. \end{aligned}$$

(C4)

For gold we have $R_A = 6.38 \,\mathrm{fm}$ and $h = 0.535 \,\mathrm{fm}$, while for lead we have $R_A=6.68 \,\mathrm{fm}$ and $h=0.546\,\mathrm{fm}$ [115]. In Eq. (C2) we have taken into account that the typical impact parameters in the hadron–hadron interaction are much smaller than the radius of nucleus ($R_A$). Indeed, the typical b in hadron–hadron collisions are $\alpha '_\mathrm{eff} Y$ or less, where $\alpha '_\mathrm{eff}$ is the effective slope of the BFKL Pomeron trajectory, which occurs in our model as a result of shadowing corrections.

Using Eq. (C2) we can re-write Eq. (B9) for proton–proton in the following form for proton–nucleus scattering:

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} = \frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{p^2_{T1}\,p^2_{T2}}\, \nonumber \\&\quad \times \int \mathrm{d}^2 k_T \,F^\mathrm{BK}_{12}\left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; k_T\right) \,\nonumber \\&\quad \times \,F^\mathrm{BK}_{A}\left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2; k_T\right) \nonumber \\&\quad +\,\frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{N^2_c - 1}\,\frac{1}{4}\left( \frac{1}{p^2_{T1}} + \frac{1}{p^2_{T2}}\right) ^2 \nonumber \\&\quad \times \int \mathrm{d}^2 k_T \,F^\mathrm{BK}_{12}\left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; \varvec{k}_T + \varvec{p}_{T,12}\right) \nonumber \\&\quad \times \,F^\mathrm{BK}_{A}\left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2;\varvec{k}_T \right) , \end{aligned}$$

(C5)

and for nucleus–nuclues scattering we have

$$\begin{aligned}&\frac{\mathrm{d}^2 \sigma }{\mathrm{d} y_1 \,\mathrm{d} y_2 \mathrm{d}^2 p_{T1} \mathrm{d}^2 p_{T2}} = \frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{p^2_{T1}\,p^2_{T2}}\, \nonumber \\&\quad \times \int \mathrm{d}^2 k_T \,F^\mathrm{BK}_{12}\left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; k_T\right) \,\,F^\mathrm{BK}_{A}\nonumber \\&\quad \times \left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2; k_T\right) \nonumber \\&\quad +\,\frac{ \tilde{a}^2_{\mathbb {P}\mathbb {P}}}{N^2_c - 1}\,\frac{1}{4}\left( \frac{1}{p^2_{T1}} + \frac{1}{p^2_{T2}}\right) ^2 \nonumber \\&\quad \times \int \mathrm{d}^2 k_T \,F^\mathrm{BK}_{A} \nonumber \\&\quad \times \left( \frac{1}{2}Y + y_1, \frac{1}{2}Y + y_2; \varvec{k}_T + \varvec{p}_{T,12}\right) \,\nonumber \\&\quad \times F^\mathrm{BK}_{A}\left( \frac{1}{2}Y - y_1, \frac{1}{2}Y - y_2;\varvec{k}_T \right) . \end{aligned}$$

(C6)