1 Introduction

Gravity in more than four dimensions has been the subject of interest in recent years for a variety of reasons. This leads to significant features of black holes (BHs) like uniqueness, dynamical stability, spherical topology, and the laws of BH mechanics. It has been found that the laws of BH mechanics are universal, while the properties of the BH are dimension dependent. The concept of higher dimensions became prominent in the 20th century with the Kaluza–Klein theory which unified gravitation and electromagnetism in five dimensions [1, 2]. Later on, development of string and M-theories led to further progress in higher dimensional gravity. String theory is the most promising candidate of quantum gravity—the fascinating theory of high energy physics. M-theory is the generalization of superstring theory that gave the concept of 11 dimensions. Charged BHs in string theory play an important role in understanding the BH entropy near the extremal limits [3]. Callan and Maldacena [4] calculated the Hawking temperature, the radiation rate, and the entropy for the extremal Reissner–Nordstr\(\ddot{\mathrm{o}}\)m BH in the context of string theory and proposed that quantum evolution of BH does not lead to information loss. Itzhaki et al. [5] studied D-brane solutions in string theory for the region where curvature is very small.

The study of BHs in higher dimensions has attracted many researchers. Tangherlini [6] was the first who generalized the Schwarzschild BH to arbitrary extra dimensions (\(D>4\)), while Myers and Perry generalized the Kerr BH [7]. There also exist black rings [8, 9] and multi BH solutions like black Saturns and multi black rings [10–13]. Carter and Neupane [14] studied stability and thermodynamics of higher dimensional Kerr–anti de Sitter BH and found stability for equal rotation parameters. Dias et al. [15] investigated perturbations of the Myers–Perry (MP) BH and found stability in five and seven dimensions. Murata [16] found instabilities of D-dimensional MP BH and concluded that there is no evidence of instability in five dimensions, however, for \(D=7,9,11,13\), the spacetime became unstable due to large angular momenta.

Galactic rotation curves are based on the measurement of red–blue shifts of emitted light from distant stars. Due to rotation of the galaxy, one side of the galaxy will appear to be blue shifted as it rotates toward the observer and the other will be red-shifted as it rotates away from the observer [17, 18]. Nucamendi et al. [19] studied the rotation curves of galaxies by measuring the frequency shifts of spherically symmetric spacetime. Lake [20] showed that the galactic potential can be linked to red–blue shifts of the galactic rotation curves. Bharadwaj and Kar [21] proposed that the flat rotation curves of the spiral galaxies can be explained by dark matter halos having anisotropic pressure. Moreover, the deflection of light ray is sensitive to the pressure of the dark matter. Faber and Visser [22] argued that observations of galactic rotation curves together with gravitational lensing describe the deduction of galactic mass and this provides information as regards the pressure of the galactic fluid. Herrera-Aguilar et al. [23] presented a useful technique to study red–blue shifts for a spiral galaxy by generalizing the galactic rotation curves for spherically symmetric spacetime to an axisymmetric metric. This approach has been used to express the Kerr BH parameters in terms of red–blue shift functions [24].

The Penrose process is related to the energy extraction from a rotating BH which depends upon the conservation of angular momentum. Chandrasekhar [25] studied the Penrose process for the Kerr BH and discussed the nature of this process and examined the limits on the extracted energy. He found that in the equatorial plane, only retrograde particles possess negative energy and the particles should remain inside the static limit (ergosphere). Bhat et al. [26] investigated the Penrose process for the Kerr–Newman BH and concluded that the energy becomes highly negative in the presence of electromagnetic field, while for neutral particles, the gain energy decreases in the presence of charge of the BH. Recently, Lasota et al. [27] presented the generalized Penrose process and stated that “for any matter or field, tapping the BH rotation energy is possible if and only if negative energy and angular momentum are absorbed by BH and no torque at the BH horizon is necessary (or possible)”. There are some other important results [28–30] in the context of Penrose process.

The collision energy of particles in the frame of the center of mass results in the formation of new particles and the energy produced in this process is known as the center of mass energy. The center of mass energy of two colliding particles is infinitely high near the event horizon of a maximally spinning Kerr BH [31]. This approach is very useful as it describes the rotating BH as a particle accelerator at the Planck energy scale. Lake [32] examined particle collisions for a non-extremal Kerr BH at the inner horizon and found center of mass energy to be finite. The center of mass energy is also analyzed for the Kerr–Newman BH, which shows the dependence on the spin and charge of the BH [33]. The same mechanism was employed on the Kerr–Newman Tuab [34] and rotating Hayward BH [35]. Other important aspects related to the center of mass energy have been explored in [36–44].

In this paper, we study the dynamics of particles for a D-dimensional MP BH in the equatorial plane. The paper is organized as follows. In the next section, we review timelike geodesics in higher dimensions. In Sect. 3, we study red–blue shifts of MP BH and formulate BH parameters in terms of red–blue shift functions. Section 4 explores the Penrose process and Sect. 5 is devoted to the study of the center of mass energy for this BH. We conclude our results in the last section.

2 Review of geodesics in higher dimensions

The generalization of a Kerr BH in higher dimensions, i.e., \(D>4\), is known as MP BH [7] and shares many properties with the Kerr BH. This plays a significant role in the exploration of gravity in higher dimensions as it provides a new vision about important features of event horizons. There are several choices of rotation axis as well as angular momentum regarding particular rotation plane. We consider a simple case by considering a single spinning parameter a. The D-dimensional MP BH in Boyer–Lindquist coordinates is given as [45, 46]

$$\begin{aligned} \mathrm{d}s^{2}= & {} -\left( \frac{\Delta -a^2\sin ^2\theta }{\rho ^2}\right) \mathrm{d}t^2 +\frac{\rho ^2}{\Delta }\mathrm{d}r^2+\rho ^2\mathrm{d}\theta ^2 \nonumber \\&+\frac{(r^2+a^2)^2-\Delta a^2\sin ^2\theta }{\rho ^2}\sin ^2\theta \mathrm{d}\phi ^2 \nonumber \\&-2\frac{(r^2+a^2)-\Delta }{\rho ^2}a\sin ^2\theta \mathrm{d}t\mathrm{d}\phi +r^2\cos ^2\theta \mathrm{d}\Omega ^2_{D-4},\nonumber \\ \end{aligned}$$
(1)

where

$$\begin{aligned} \rho ^{2}= & {} r^{2}+a^2\cos \theta ^{2},\quad \Delta =r^2+a^2-\mu r^{5-D},\\ \mu= & {} \frac{16\pi GM}{(D-2)\Omega _{(D-2)}},\quad \Omega _{D-2}=\frac{2\pi ^{\frac{D-1}{2}}}{\Gamma \left( \frac{D-1}{2}\right) }, \end{aligned}$$

and

$$\begin{aligned} \Omega ^{2}_{D-2}= & {} \mathrm{d}\theta ^{2}_{1}+\sin ^{2}\theta _{1}\mathrm{d}\theta ^{2}_{2}+ \sin ^{2}\theta _{1}\sin ^{2}\theta _{2}\mathrm{d}\theta ^{2}_{3}\\&+\cdots + \prod ^{D-3}_{\lambda =1}\sin ^{2}\theta _{\lambda }\mathrm{d}\theta ^{2}_{D-2} \end{aligned}$$

describes the \((D-4)\) unit sphere. This metric is for an asymptotically flat, vacuum spacetime with ADM mass \(\mu \) and D may be even or odd. For \(D=4\) it reduces to the Kerr BH, while \(a=0\) leads to the Schwarzschild BH. The event horizon of (1) is the largest root of \(\Delta =0\),

$$\begin{aligned} r^2_{h}+a^2-\mu r^{5-D}_{h}=0. \end{aligned}$$

The extremal limit exists for \(D=4,5\) \(\left( a<\frac{\mu }{2}\ \mathrm{and}\ a<\sqrt{\mu }\right) \). For \(D\ge 6\), there is only one positive root when \(a>0\), which indicates that there is no extremal limit in higher dimensions [46]. The behavior of horizons along the spin parameter can be seen in Fig. 1.

Fig. 1
figure 1

Horizons with respect to a

Full size image

The particle motion can be described by the Lagrangian

$$\begin{aligned} \mathcal {L}=\frac{1}{2}g_{\nu \sigma }\dot{x}^{\nu }\dot{x}^{\sigma }, \end{aligned}$$
(2)

where \(\dot{x}^{\nu }=u^{\nu }=\mathrm{d}x^{\nu }/\mathrm{d}\tau \) and \(u^{\nu }\) is the particle’s D-velocity and \(\tau \) is the affine parameter. In the equatorial plane (\(\theta =\frac{\pi }{2},~\dot{\theta }=0\)), Eq. (2) takes the form

$$\begin{aligned} 2\mathcal {L}= & {} -\left( 1-\frac{\mu }{r^{D-3}}\right) \dot{t}^2 -2a\left( \frac{\mu }{r^{D-3}}\right) \dot{t}\dot{\phi } +\frac{r^2}{\Delta }\dot{r}^2\nonumber \\&+ \left( r^2+a^2+\frac{\mu a^2}{r^{D-3}}\right) \dot{\phi }^2. \end{aligned}$$
(3)

The generalized momenta for (1) are calculated as

$$\begin{aligned} -k_{t}= & {} -\left( 1-\frac{\mu }{r^{D-3}}\right) \dot{t} -\left( \frac{a\mu }{r^{D-3}}\right) \dot{\phi }=E,\end{aligned}$$
(4)
$$\begin{aligned} k_{\phi }= & {} -\left( \frac{a\mu }{r^{D-3}}\right) \dot{t}+\left( r^2+a^2+\frac{\mu a^2}{r^{D-3}}\right) \dot{\phi }=L,\end{aligned}$$
(5)
$$\begin{aligned} k_{r}= & {} \frac{r^2}{\Delta }\dot{r}, \end{aligned}$$
(6)

where a dot represents the derivative with respect to \(\tau \). We find that the Lagrangian is independent of t and \(\phi \), therefore \(k_{t}\) and \(k_{\phi }\) are conserved and hence this describes stationary and axisymmetric characteristics of MP BH.

The Hamiltonian can be written as

$$\begin{aligned} H=k_{t}\dot{t}+k_{\phi }\dot{\phi }+k_{r}\dot{r}-\mathcal {L}. \end{aligned}$$
(7)

For the metric (1), it takes the following form:

$$\begin{aligned} 2H= & {} -\left[ \left( 1-\frac{\mu }{r^{D-3}}\right) \dot{t} +\left( \frac{a\mu }{r^{D-3}}\right) \dot{\phi }\right] \dot{t}\nonumber \\&+\left[ -\left( \frac{a\mu }{r^{D-3}}\right) \dot{t}+\left( r^2+a^2+\frac{\mu a^2}{r^{D-3}}\right) \dot{\phi }\right] \dot{\phi }+\frac{r^2}{\Delta }\dot{r}^2 \nonumber \\= & {} -E\dot{t}+L\dot{\phi }+\frac{r^2}{\Delta }\dot{r}^2=\delta =\text {constant}, \end{aligned}$$
(8)

where \(\delta =0,-1,1\) describe null (lightlike), timelike, and spacelike geodesics. From Eqs. (4) and (5), we obtain

$$\begin{aligned} \dot{t}= & {} \frac{1}{\Delta } \left[ \frac{a\mu }{r^{D-3}}E+\left( 1-\frac{a\mu }{r^{D-3}}\right) L\right] ,\end{aligned}$$
(9)
$$\begin{aligned} \dot{\phi }= & {} \frac{1}{\Delta }\left[ \left( r^2+a^2+\frac{\mu a^2}{r^{D-3}}\right) E-\frac{a\mu }{r^{D-3}}L\right] . \end{aligned}$$
(10)

Inserting Eqs. (9) and (10) into (8), we find the radial equation of motion

$$\begin{aligned} r^2\dot{r}^2=r^2E^2+\frac{\mu }{r^{D-3}}(aE-L)^2+(a^2E^2-L^2)+\Delta \delta .\nonumber \\ \end{aligned}$$
(11)

Equations (9)–(11) are very important as they can be used to study various features related to particle motion around (1). Following some algebraic manipulation, the energy and angular momentum can be written as

$$\begin{aligned} E= & {} \frac{1}{\sqrt{\zeta _{\pm }}}\left[ 1-\mu y^{D-3}\mp a\sqrt{(D-3)(\mu /2) y^{D-1}}\right] , \nonumber \\ L= & {} \mp \frac{\sqrt{(D-3)(\mu /2)y^{D-4}}}{y\zeta _{\mp }}\nonumber \\&\times \left[ 1+a^2y^2\pm \sqrt{\frac{(\mu /2) y^{D-1}}{D-3}}\right] , \end{aligned}$$
(12)

where \(y=1/r\) and \(\zeta _{\pm }=1-(D-1)(\mu /2)y^{D-3}\pm 2a\sqrt{(D-3)(\mu /2)y^{D-1}}\). These are the same as obtained in [45] for \(M=\mu /2\) (M is a parameter related to the BH mass). Here, we do not consider this substitution, as we are interested in finding our results with the ADM mass.

3 Red–blue shifts of Myers–Perry BH

This section is devoted to the study of red–blue shifts in higher dimensions for MP BH. Herrera-Aguilar et al. [23] discussed red–blue shifts for an axially symmetric spacetime and presented a convenient approach to study the galactic rotational curves of spiral galaxies. Since spiral galaxies possess axial symmetry, this method provides information as regards the interior of the gravitational field of such galaxies. Herrera-Aguilar [24] extended this technique for the Kerr BH and found parameters in terms of red–blue shifts in the equatorial plane. Following [23, 24], we generalize these results for the MP BH. We consider two observers \(O_{d}\) and \(O_{e}\), corresponding to detector and light emitter (star) placed at points \(P_{d}\) and \(P_{e}\), respectively. The detector and emitter possess D-velocities \(u^{\nu }_{d}\) and \(u^{\nu }_{e}\). We assume that the stars are moving in the galactic plane such that the polar angle is fixed (\(\theta =\frac{\pi }{2}\)). In this case, we have \(u^{\nu }_{e}=(u^{t},~u^{r},0,\ldots ,0,~u^{\phi })_{e}\), where \(u^{\nu }=\mathrm{d}x^{\nu }/\mathrm{d}\tau \) and \(\tau \) is the proper time of the particle. The D-velocity of the detector, \(u_{d}=(u^{t},~u^{r},0,\ldots ,0,~u^{\phi })_{d}\), is located far away from the source. The component \(u^{\phi }\) is related to the observer’s dragging at point \(P_{d}\) due to galactic rotation and its effect is present when measuring red–blue shifts in our galaxy (Milky Way) or nearby galaxies [23].

The general frequency expression of photon measured by an observer is

$$\begin{aligned} \omega _{c}=-k_{\nu }u^{\nu }_{c}|_{P_{c}}, \end{aligned}$$
(13)

where \(k^{\nu }=(k^{t},k^{r},0,\ldots ,0,k^{\phi })_{c}\) is the D-momentum in the equatorial plane and the index c corresponds to emitter (e) or detector (d) for the spacetime at point \(P_{c}\). The light frequencies detected by an observer at \(P_{d}\) and measured by an observer moving with the emitted particle at point \(P_{e}\) are

$$\begin{aligned} \omega _{d}=-k_{\nu }u^{\nu }_{d},\quad \omega _{e}=-k_{\nu }u^{\nu }_{e}. \end{aligned}$$
(14)

The frequency shift corresponding to emission as well as detection has the form

$$\begin{aligned} 1+z=\frac{\omega _{e}}{\omega _{d}} =\frac{(Eu^{t}-Lu^{\phi }-g_{rr}u^{r}k^{r})|_{e}}{(Eu^{t}-Lu^{\phi } -g_{rr}u^{r}k^{r})|_{d}}. \end{aligned}$$
(15)

Since we have considered circular orbital motion (\(u^{r}=0\)), the above equation becomes

$$\begin{aligned} 1+z=\frac{(Eu^{t}-Lu^{\phi })|_{e}}{(Eu^{t}-Lu^{\phi })|_{d}}= \frac{u^{t}_{e}-b_{e}u^{\phi }_{e}}{u^{t}_{d}-b_{d}u^{\phi }_{d}}, \end{aligned}$$
(16)

where \(b=\frac{L}{E}\) is the impact parameter for the observer located at infinity. This parameter is zero when it is measured from either side of the center of galaxy. In this case, Eq. (16) can be written as

$$\begin{aligned} 1+z= \frac{u^{t}_{e}}{u^{t}_{d}}. \end{aligned}$$
(17)

Subtracting (17) from (16), the kinematical red shift can be obtained:

$$\begin{aligned} z_{\kappa }=z-z_{c}= \frac{u^{t}_{e}u^{\phi }_{d}b_{d}-u^{t}_{d}u^{\phi }_{e}b_{e}}{u^{t}_{d} (u^{t}_{d}-b_{d}u^{\phi }_{d})}. \end{aligned}$$

It is important to mention here that the impact parameter remains constant along the path of the photon, i.e. \(b_{e}=b_{d}\). This is due to the fact that energy and angular momentum are preserved from emission to detection along the null geodesics. We are interested in red–blue shifts from either side of the galactic center, which requires two values of b to calculate the red–blue shifts. The impact parameter can be calculated from the radial null geodesic \(k^{\nu }k_{\nu }=0\) [23],

$$\begin{aligned} b_{\pm }=\frac{-g_{t\phi } \pm \sqrt{g^{2}_{t\phi }-g_{tt}g_{\phi \phi }}}{g_{tt}}, \end{aligned}$$
(18)

where \(b_{-}\) and \(b_{+}\) lead to the red–blue shifts of the photons emitted from an object moving away or approaching toward a far away observer located at infinity [23],

$$\begin{aligned} z_\mathrm{red}=\frac{u^{t}_{e}u^{\phi }_{d}b_{d_{-}}-u^{t}_{d}u^{\phi }_{e} b_{e_{-}}}{u^{t}_{d}(u^{t}_{d}-u^{\phi }_{d}b_{d_{-}})},\end{aligned}$$
(19)
$$\begin{aligned} z_\mathrm{blue}=\frac{u^{t}_{e}u^{\phi }_{d}b_{d_{+}}-u^{t}_{d}u^{\phi }_{e} b_{e_{+}}}{u^{t}_{d}(u^{t}_{d}-u^{\phi }_{d}b_{d_{+}})}, \end{aligned}$$
(20)

where \(z_\mathrm{red}\ne z_\mathrm{blue}\), in general. The angular velocity can be defined as

$$\begin{aligned} \frac{u^{\phi }_{d}}{u^{t}_{d}}=\frac{\mathrm{d} \phi }{\mathrm{d}t} \equiv \Omega _{d}. \end{aligned}$$
(21)

When the observer is located far away from the source (emitter) such that \(u^{\phi }_{d}<<u^{t}_{d}\), then \(\Omega _{d}<<1\). Using Eqs. (21), (19), and (20) we have

$$\begin{aligned} z_\mathrm{red}=\frac{u^{t}_{e}\Omega _{d} b_{d_{-}}-u^{\phi }_{e}b_{e_{-}}}{u^{t}_{d}(1-\Omega _{d}b_{d_{-}})},\end{aligned}$$
(22)
$$\begin{aligned} z_\mathrm{blue}=\frac{u^{t}_{e}\Omega _{d} b_{d_{+}}-u^{\phi }_{e}b_{e_{+}}}{u^{t}_{d}(1-\Omega _{d}b_{d_{+}})}. \end{aligned}$$
(23)

In order to calculate red–blue shifts for the MP BH, we consider the D-velocity components corresponding to (9) and (10) for the circular orbits in the equatorial plane

$$\begin{aligned} u^{t}= & {} \frac{1}{\Delta }\left[ \frac{(a\mu )E-(r^{D-3}-\mu )L}{r^{D-3}}\right] ,\end{aligned}$$
(24)
$$\begin{aligned} u^{\phi }= & {} \frac{1}{\Delta }\left[ \frac{(r^{D-1}+a^2r^{D-3}+a^2\mu )E-(a\mu )L}{r^{D-3}}\right] , \end{aligned}$$
(25)

where

$$\begin{aligned} E= & {} \frac{r^{\frac{D-1}{2}}-\mu r^{\frac{5-D}{2}}\mp a [(D-3)(\mu /2)]^{\frac{1}{2}}}{r^{\frac{D-1}{4}}[r^{\frac{D-1}{2}}-(D-1)(\mu /2)r^{\frac{5-D}{2}}\pm 2a[(D-3)(\mu /2)]^{\frac{1}{2}}]^{\frac{1}{2}}},\nonumber \\ \end{aligned}$$
(26)
$$\begin{aligned} L= & {} \frac{\pm ((D-3)(\mu /2))^{\frac{1}{2}}[r^2+a^2 \mp 2a(\frac{(\mu /2)}{D-3})^{\frac{1}{2}}r^{\frac{5-D}{2}}]}{r^{\frac{D-1}{4}}[r^{\frac{D-1}{2}}-(D-1)(\mu /2)r^{\frac{5-D}{2}}\pm 2a[(D-3)(\mu /2)]^{\frac{1}{2}}]^{\frac{1}{2}}},\nonumber \\ \end{aligned}$$
(27)

here ± sign describe direct and retrograde objects which may be emitter or detector with respect to angular velocity. Using Eqs. (26) and (27) in (24) and (25), we obtain

$$\begin{aligned} u^{\phi }= & {} \frac{\pm [(D-3)(\mu /2)]^{\frac{1}{2}}}{r^{\frac{D-1}{4}}[r^{\frac{D-1}{2}}-(D-1)(\mu /2)r^{\frac{5-D}{2}}\pm 2a[(D-3)(\mu /2)]^{\frac{1}{2}}]^{\frac{1}{2}}},\nonumber \\ \end{aligned}$$
(28)
$$\begin{aligned} u^{t}= & {} \frac{\pm [(D-3)(\mu /2)]^{\frac{1}{2}}[r^{\frac{D-1}{2}}\pm ((D-3)(\mu /2))^{\frac{1}{2}}]}{r^{\frac{D-1}{4}}[r^{\frac{D-1}{2}}-(D-1)(\mu /2)r^{\frac{5-D}{2}}\pm 2a[(D-3)(\mu /2)]^{\frac{1}{2}}]^{\frac{1}{2}}}.\nonumber \\ \end{aligned}$$
(29)

The angular velocity of the orbiting source (emitter or detector) around the MP BH can easily be calculated from Eqs. (28) and (29):

$$\begin{aligned} \Omega _{\pm }=\frac{\pm [(D-3)(\mu /2)]^{\frac{1}{2}}}{r^{\frac{D-1}{2}}\pm [(D-3)(\mu /2)]^{\frac{1}{2}}}. \end{aligned}$$
(30)

The impact parameter for the equatorial circular orbits in D dimensions can be obtained from Eq. (18),

$$\begin{aligned} b_{\pm }=\frac{-a\mu \pm r^{D-3}[r^2+a^2-\mu r^{5-D}]^{\frac{1}{2}}}{r^{D-3}-\mu }. \end{aligned}$$
(31)

The red–blue shifts for (1) are found from Eqs. (22) and (23):

$$\begin{aligned} z_\mathrm{red}= & {} \frac{\pm \sqrt{(D-3)(\mu /2)}}{\beta \gamma \left( r^{\frac{D-1}{2}}_{d}\pm a\sqrt{(D-3)(\mu /2)}\right) } \nonumber \\&\times \alpha \left( r^{\frac{{D-1}}{2}}_{d}-r^{\frac{{D-1}}{2}}_{e}\right) \nonumber \\&\times \left[ a\mu +r^{D-3}_{e}\sqrt{r^2_{e}+a^2-\mu r^{D-3}_{e}}\right] , \end{aligned}$$
(32)
$$\begin{aligned} z_\mathrm{blue}= & {} \frac{\pm \sqrt{(D-3)(\mu /2)}}{\beta \varrho (r^{\frac{D-1}{2}}_{d}\pm a\sqrt{(D-3)(\mu /2)})}\nonumber \\&\times \alpha \left( r^{\frac{{D-1}}{2}}_{d}-r^{\frac{{D-1}}{2}}_{e}\right) \nonumber \\&\times \left[ a\mu -r^{D-3}_{e}\sqrt{r^2_{e}+a^2-\mu r^{D-3}_{e}}\right] , \end{aligned}$$
(33)

where \(r_{d}\) and \(r_{e}\) are the orbit radii of detector and emitter, and

$$\begin{aligned} \alpha= & {} r^{\frac{{D-1}}{4}}_{d}\left[ r^{\frac{{D-1}}{2}}_{d}- (D-1)(\mu /2)r^{\frac{{5-D}}{2}}_{d}\pm 2a\sqrt{(D-3)(\mu /2)}\right] ^{\frac{1}{2}},\\ \beta= & {} r^{\frac{{D-1}}{4}}_{e}\left[ r^{\frac{{D-1}}{2}}_{e}- (D-1)(\mu /2)r^{\frac{{5-D}}{2}}_{e}\pm 2a\sqrt{(D-3)(\mu /2)}\right] ^{\frac{1}{2}},\\ \gamma= & {} r^{\frac{D-1}{2}}_{d}(r^{D-3}_{e}-\mu )\pm ar^{D-3}_{e}\sqrt{(D-3)(\mu /2)} \\&\pm \sqrt{(D-3)(\mu /2)}r^{D-3}_{e}\sqrt{r^2_{e}+a^2-\mu r^{D-3}_{e}}, \\ \varrho= & {} r^{\frac{D-1}{2}}_{d}(r^{D-3}_{e}-\mu )\pm ar^{D-3}_{e}\sqrt{(D-3)(\mu /2)} \\&\mp \sqrt{(D-3)(\mu /2)}r^{D-3}_{e}\sqrt{r^2_{e}+a^2-\mu r^{D-3}_{e}}. \end{aligned}$$

The relation \(b_{e}=b_{d}\) yields the equation relating the radius of emitter and detector,

$$\begin{aligned}&r^{2(D-2)}_{d}-\mu r^{D-1}_{d}-r^{2(D-3)}_{d}(b^2_{e}-a^2) \nonumber \\&\quad +2b_{e}\mu (b_{e}-a)r^{D-3}_{d}-(\mu )^2(b^2_{e}-a^2)^2=0. \end{aligned}$$
(34)

When the detector is far away from the source and \(r_{d}>>\mu \ge a\), the red–blue shifts reduce to

$$\begin{aligned} z_\mathrm{red}&=\frac{\pm \sqrt{(D-3)(\mu /2)} \left[ a\mu +r^{D-3}_{e}\sqrt{r^2_{e}+a^2-\mu r^{D-3}_{e}}\right] }{\beta (r^{D-3}_{e}-\mu )},\nonumber \\ \end{aligned}$$
(35)
$$\begin{aligned} z_\mathrm{blue}&=\frac{\pm \sqrt{(D-3)(\mu /2)} \left[ a\mu -r^{D-3}_{e}\sqrt{r^2_{e}+a^2-\mu r^{D-3}_{e}}\right] }{\beta (r^{D-3}_{e}-\mu )}.\nonumber \\ \end{aligned}$$
(36)

From Eqs. (35) and (36), the parameters of the MP BH can be expressed in terms of red–blue shift of the photons emitted from the source. The spin parameter in terms of red–blue shifts is given as

$$\begin{aligned} a^2=\frac{r^{3(D-3)}_{e}(r^{5-D}_{e}-\mu )(z_\mathrm{red}+z_\mathrm{blue})^2}{\mu ^2(z_\mathrm{red}-z_\mathrm{blue})^2-r^{2(D-3)}_{e}(z_\mathrm{red}+z_\mathrm{blue})^2}. \end{aligned}$$
(37)

The mass parameter corresponding to red–blue shifts can be obtained from the following expression:

$$\begin{aligned}&2(D-3)r^{4D-14}_{e}\mu (z_\mathrm{red}+z_\mathrm{blue})^2(r^{5-D}_{e}-\mu ) (r^{D-3}_{e}-\mu )^4 \nonumber \\&\qquad \times [\mu ^2(z_\mathrm{red}-z_\mathrm{blue})^2-r^{2(D-3)}_{e}(z_\mathrm{red}+z_\mathrm{blue})^2] \nonumber \\&\quad =[2\mu ^3r^{3D-11}_{e}(D-3)(r^{5-D}_{e}-\mu ) -(\mu ^2(z_\mathrm{red}-z_\mathrm{blue})^2\nonumber \\&\qquad -r^{2(D-3)}_{e} (z_\mathrm{red}+z_\mathrm{blue})^2)\times (r^{D-3}_{e}-(D-1)(\mu /2))\nonumber \\&\qquad \times (r^{D-3}_{e}-\mu )^2]^2. \end{aligned}$$
(38)

Equations (37) and (38) reduce to the results of Kerr BH when \(D=4\). These equations may provide a useful model for the researchers interested in higher dimensions using experimental data. One can easily observe how the photons emitted from the source (e.g. stars) can be red- or blue-shifted near the higher dimensional BH. The mass as well as the rotation of MP BH affects the emitted photons. Another interesting phenomenon caused by the BH rotation is the Penrose process that takes place within the ergosphere. In the next section, we examine the particle motion and its consequences as it enters the ergosphere.

3.1 The Penrose process

The rotation of a spinning BH corresponds to a reservoir of usable energy and is related to the properties of particles (e.g. photons) inside the ergosphere (the stationary limit surface) where the particles can orbit with total negative energy with respect to a distant observer. The orbits with negative energies have negative angular momenta with respect to the BH. Non-rotating BHs do not have such stationary limit surfaces; however, rotating BHs (e.g. Kerr BH) do have such surfaces, called ergospheres. The particles orbiting with negative energy can exchange energy with other particles. It was first pointed out by Penrose that this process can be used to extract energy from the spinning BH. Following [25], we study the Penrose process in higher dimensions for the MP BH. Equation (11) gives

$$\begin{aligned}&E^2[r^{D-3}(r^2+a^2)+\mu a^2]-2a\mu EL -L^2(r^{D-3}-\mu )\\&\quad + r^{D-3}\delta \Delta =0. \end{aligned}$$

Solving this equation for E and L, we obtain

$$\begin{aligned} E= & {} \frac{a\mu L \pm \sqrt{r^{2(D-3)}L^2-r^{D-3}\delta [r^{D-3}(r^2+a^2)+ a^2\mu ]}\sqrt{\Delta }}{r^{D-3}(r^2+a^2)+a^2\mu },\nonumber \\ \end{aligned}$$
(39)
$$\begin{aligned} L= & {} \frac{-a\mu \pm \sqrt{r^{2(D-3)}E^2+(r^{D-3}-\mu )\delta r^{D-3}}\sqrt{\Delta }}{r^{D-3}-\mu }, \end{aligned}$$
(40)

where we have used the following identity:

$$\begin{aligned} r^2\Delta -a^2\mu ^2= & {} [r^{D-3}(r^2+a^2)+a^2\mu ](r^{D-3}-\mu ). \end{aligned}$$
(41)

Equation (39) can describe conditions for which E can be negative (seen by an observer at infinity).

First we assign \(E=1\) to the particle at rest at infinity with unit mass [25]. We consider \(+\) sign of Eq. (39) which requires \(L<0\) for \(E<0\) and

$$\begin{aligned} a^2L^2\mu ^2 >\Delta [L^2r^{D-3}-(r^{2(D-3)}(r^2+a^2)+a^2\mu r^{D-3})]\delta . \end{aligned}$$

Using Eq. (41), this can be written as

$$\begin{aligned}&[r^{2(D-3)}(r^2+a^2)+a^2\mu r^{D-3}]\\&\quad \times \left[ L^2\left( 1-\frac{\mu }{r^{D-3}}\right) -\delta \Delta \right] <0. \end{aligned}$$

It follows from the above equation that \(E<0\) if and only if \(L<0\) and

$$\begin{aligned} (r^{D-3}-\mu )<\frac{r^{D-3}\Delta }{L^2}\delta . \end{aligned}$$

We conclude that in higher dimensions only particles with retrograde motion can have negative energy on the equatorial plane. Also, it is necessary that the particle remains inside the ergosphere.

3.2 The original Penrose process

The Penrose process describes that the particle with positive energy enters into the ergosphere and breaks up into two parts such that one will have a negative energy, while the other part will have positive energy. The particle with negative energy will be absorbed by the BH and the particle with positive energy will escape to infinity. The particle leaving the ergosphere will have more energy than the original particle. The whole process results in a decreasing mass and angular momentum of the BH. Hence, the rotational energy is extracted from the BH in this process [47]. Here, we suppose that the photon absorbed by the BH (by crossing the event horizon) possesses negative energy, while the photon that escapes to infinity has an energy exceeding the original particle (which came from infinity). Let \( E^{(1)}=1,~L^{(1)},~E^{(2)},~L^{(2)},~E^{(3)},~ L^{(3)}\) be the energies and angular momenta of the original particle arriving from infinity and the two photons (one that enters the event horizon and the other which escapes to infinity). The angular momentum of the particle arriving from infinity by timelike geodesics can be obtained from Eq. (40) by setting \(E=1\) and \(\delta =-1\),

$$\begin{aligned} L^{(1)}=\frac{-a\mu +\sqrt{\mu r^{D-3}}\sqrt{\Delta }}{r^{D-3}-\mu }=\sigma ^{(1)}. \end{aligned}$$
(42)

The relationship between energies and angular momenta of the photon that crosses the event horizon and the photon which escapes to infinity can be obtained by setting \(\delta =0\) and considering both negative and positive signs in Eq. (40),

$$\begin{aligned} L^{(2)}= & {} \frac{\left[ -a\mu -\sqrt{\Delta }r^{D-3}\right] E^{(2)}}{r^{D-3}-\mu }=\sigma ^{(2)}E^{(2)},\end{aligned}$$
(43)
$$\begin{aligned} L^{(3)}= & {} \frac{\left[ -a\mu -\sqrt{\Delta }r^{D-3}\right] E^{(3)}}{r^{D-3}-\mu }=\sigma ^{(3)}E^{(3)}. \end{aligned}$$
(44)
Fig. 2
figure 2

Energy gain versus a

Full size image
Fig. 3
figure 3

Center of mass energy with respect to r for \(a=0.25\) (left) and \(a=0.6\) (right). Here, the curves show \(E_\mathrm{cm}/\sqrt{m^2_{0}}\), while vertical dashed lines are event horizons

Full size image

The conservation of energy and of angular momentum yield

$$\begin{aligned}&E^{(2)}+E^{(3)}=E^{(1)}=1,\quad L^{(2)}+L^{(3)}=\sigma ^{(2)}E^{(2)}\\&\qquad \quad +\sigma ^{(2)}E^{(3)}=L^{(1)}=\sigma ^{(1)}, \end{aligned}$$

which implies that

$$\begin{aligned} E^{(2)}=\frac{\sigma ^{(1)}-\sigma ^{(3)}}{\sigma ^{(2)}-\sigma ^{(3)}}, \quad E^{(3)}=\frac{\sigma ^{(2)}-\sigma ^{(1)}}{\sigma ^{(2)}-\sigma ^{(3)}}. \end{aligned}$$

Inserting \(\sigma ^{(1)},~\sigma ^{(2)}\), and \(\sigma ^{(3)}\) from Eqs. (42)-(44), we obtain

$$\begin{aligned} E^{(2)}=-\frac{1}{2}\left[ \sqrt{\frac{\mu }{r^{D-3}}}-1\right] , ~ E^{(3)}=\frac{1}{2}\left[ \sqrt{\frac{\mu }{r^{D-3}}}-1\right] . \end{aligned}$$

The photon that escapes to infinity has more energy than the original particle \(E^{(1)}=1\). Thus the gained energy (\(\Delta E\)) can be written as

$$\begin{aligned} \Delta E=\frac{1}{2}\left[ \sqrt{\frac{\mu }{r^{D-3}}}-1\right] =-E^{(2)}. \end{aligned}$$

According to the Penrose process, the particle arriving from infinity can attain a maximum gain in energy at the event horizon. Thus

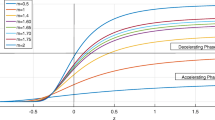
$$\begin{aligned} \Delta E\le \frac{1}{2}\left[ \sqrt{\frac{\mu }{r^{D-3}_{h+}}}-1\right] . \end{aligned}$$

The maximum energy gain by the Kerr BH (in extreme limit) can be achieved for \(D=4\), i.e., \(\Delta E=0.207\). The energy gain for a MP BH can be seen in Fig. 2. It is found that for \(D=4\) we have \(\Delta E\) for the Kerr BH. For \(D=5\), the energy gain is higher than all dimensions, while for \(D=6\), it has an almost similar behavior as the Kerr BH. We have shown the energy gain for the particles with positive spin as the behavior for the negative spin remains the same due to symmetry. In all (11) dimensions, the energy gain has an increasing behavior but its value varies with respect to dimensions.

4 Center of mass energy in higher dimensions

The rotating BHs have many interesting features, such as their effects on the frequency shift on the photons that are traveling near them as well as the extraction of rotational energy as the photon with positive energy enters into the static limit of the BH. One of the important features of rotating BHs is that they can also act as particle accelerators. In this section, we study the center of mass energy (\(E_\mathrm{cm}\)) of the accelerating particles near the MP BH in the equatorial plane. The center of mass energy is defined as the sum of the rest masses and their kinetic energies of the two colliding particles. It depends upon the nature of interacting particles as well as astrophysical objects (BH or naked singularity) and the gravitational field surrounding such objects. It is interesting to study the collision of particles, as it is a naturally occurring process in the universe. We consider two neutral colliding particles having rest masses \(m_{1}\) and \(m_{2}\). The conserved energies and angular momenta of two particles are \(E_{1}\), \(E_{2}\), \(L_{1}\), and \(L_{2}\). The angular momentum of the \(i\mathrm{th}\) particle is defined as

$$\begin{aligned} k^{\nu }_{i}=m_{i}u^{\nu }_{i}, \quad i=1,2. \end{aligned}$$
(45)

The center of mass energy of the colliding particles is given as

$$\begin{aligned} E^2_\mathrm{cm}=-k^{\nu }_{i}k_{i\nu }. \end{aligned}$$
(46)

Using Eq. (45) in (46), we obtain

$$\begin{aligned} \frac{E_\mathrm{cm}}{\sqrt{2m_{1}m_{2}}}=\sqrt{\frac{(m_{1}- m_{2})^2}{2m_{1}m_{2}}+(1-g_{\nu \eta }u^{\nu }_{1}u^{\eta }_{2})}. \end{aligned}$$

Substituting the values of \(g_{\nu \eta }\), \(u_{1}^{\nu }\), and \(u_{2}^{\eta }\), the center of mass energy in D dimensions becomes

$$\begin{aligned}&\frac{E_\mathrm{cm}}{\sqrt{2m_{1}m_{2}}}=\left[ \frac{(m_{1}- m_{2})^2}{2m_{1}m_{2}}+\frac{1}{r^{D-3}\Delta }\right. \\&\quad \times \left[ r^{D-3}\Delta + E_{1}E_{2}(r^{D-1}+a^2r^{D-3}+a^2\mu ) \right. \\&\quad \left. \left. -(E_{2}L_{1}\!+\! E_{1}L_{2})(a\mu )\!-\!L_{1}L_{2}(r^{D-3}\!-\!\mu )\!-\!\sqrt{R_{1}R_{2}}\right] \right] ^{\frac{1}{2}}, \end{aligned}$$

where

$$\begin{aligned}&R_{i}=r^{D-1}E^2_{i}\!+\!\mu (aE_{i}\!-\!L_{i})^2\!-\!r^{D-3}L^2_{i}-r^{D-1}+\mu r^2,\\&\quad i=1,2. \end{aligned}$$

For the sake of simplicity, we take \(m_{1}=m_{2}=m_{0}\) and \(E_{1}=E_{2}=E=1\) such that the above equation takes the form

$$\begin{aligned}&\frac{E_\mathrm{cm}}{\sqrt{m^2_{0}}}=\left[ \frac{1}{r^{D-3}\Delta }\left[ r^{D-3}\Delta + (r^{D-1}+a^2r^{D-3}+a^2\mu ) \right. \right. \\&\left. \left. -(L_{1}+L_{2})(a\mu )-L_{1}L_{2}(r^{D-3}-\mu )-\sqrt{R_{1}R_{2}}\right] \right] ^{\frac{1}{2}}, \end{aligned}$$

where

$$\begin{aligned} R_{i}=\mu (a-L_{i})^2-r^{D-3}L^2_{i}+\mu r^2, \quad i=1,2. \end{aligned}$$

For \(D=4\), the above equation reduces to [31]. Figure 3 shows the behavior of the center of mass energy for \(M=1,L_{1}=2,L_{2}=2.5\) up to 11 dimensions. We found that the center of mass energy has decreasing behavior in all dimensions.

5 Final remarks

When a light wave (from an approaching galaxy which is moving toward an observer) gets scrunched to the shorter wavelength, this is known as the galactic blue shift. On the other hand, if a light wave from a galaxy moving away from the observer gets stretched to the longer wavelength then this is called galactic red shift. Slipher discovered that the Andromeda galaxy possesses a large blue shift which indicates that this galaxy moves toward the Earth. He further investigated other spiral galaxies and found that most of them have a large red shift, indicating that they are moving away from us. Hubble observations indicate that relative to the Earth and all the observed galactic objects, galaxies are receding in every direction. The velocities calculated from their observed red shifts are directly proportional to their distance from each other as well as from the Earth. Hubble was the pioneer in explaining the expanding universe and red shift phenomena [48, 49].

It is well known that there is a supermassive BH (SgrA*) in the center of Milky Way, as is the case in many other spiral galaxies. In this paper, we assume a higher dimensional MP BH as a supermassive BH at the galactic center. Motivated by [23, 24], we generalize the mass and angular momentum parameter in arbitrary extra dimensions in terms of red–blue shifts of the photons emitted from circular timelike geodesic and traveling along the null geodesic. For this purpose, we have first calculated red–blue shifts of the photons in higher dimensions for an observer located far away. We have taken circular as well as equatorial orbits to find these shifts. We have expressed the corresponding mass, rotation parameter and radius of the detector in terms of red–blue shifts. In this way, we have generalized the results for the Kerr BH. We have only discussed the analytical model, however, these results may be useful if they can be calculated using the observational data. The generalized results can provide information as regards the behavior of BH parameters in dimensions \(D\ge 4\).

It is believed that the supermassive BHs (powering the active galaxies and quasars) are the rapidly rotating BHs. Such BHs produce powerful jets of gas (whose direction is sometimes stable over a million of years) whose source of energy may be the rotation of BH. It may be possible that this rotational energy is extracted due to the Penrose process [47]. Following [25], we have studied the Penrose process for the MP BH. We have found that a particle will have negative energy for a retrograde motion (\(L<0\)) in higher dimensions. We have also seen that the energy gain of the particle is dimension dependent. The energy gains for \(D=4\) and \(D=6\) have the same values, while for \(D=5\), it has the highest value.

We have also examined the influence of higher dimensions on the center of mass energy of two colliding particles. We have plotted \(E_\mathrm{cm}\) by considering two different values of the rotating parameters. The center of mass energy decreases with increasing radius. For \(a=0.25\), the center of mass energy for \(D=6~\text {and}~ 8\), it lies inside the event horizon, while for other dimensions, it crosses the event horizon. For \(a=0.6\), the center of mass energy crosses the event horizon in all dimensions. In both cases, the center of mass energy for \(D=4\) is greater than that of \(D\ge 5\). Finally, we conclude that the motion of particles in higher dimensions experiences a very different behavior than the four dimensions.