1 Introduction

The advantages of working in lower-dimensional gravity, specifically in \( 2+1\) dimensions has been highlighted extensively during the recent decades. The interest started all with the discovery of a \(2+1\)-dimensional black hole solution by Banados, Teitelboin and Zanelli (BTZ) [1–4]. The physical source of the BTZ black hole was a cosmological constant, which was subsequently extended with the presence of different sources [5–17]. How significant are these sources physically? The addition of scalar [18–23] and electromagnetic fields, both linear and non-linear, has almost become a routine, while exotic and phantom fields also found room of applications in the problem. A source that is less familiar is a cloud of strings [24–34], which was considered in Einstein’s general relativity. Within this context in \(3+1\) dimensions the importance of a string cloud has been attributed to the action-at-a distance interaction between particles. For a detailed geometrical description of a string cloud we refer to [24–34]. In this study we extend such a source to the \(f\left( R\right) =R^{n}\) gravity which is a modified version of general relativity [35–39]. In D-dimensional spacetime the energy-momentum tensor for a string cloud is represented by \(T_{\mu }^{\nu }=\frac{\xi }{r^{D-2}}\mathrm{diag}\left( 1,1,0,0,\ldots ,0\right) \) where \(\xi \) is a positive constant. In 3 dimensions, which will be our concern here, this amounts to \( T_{0}^{0}=T_{1}^{1}=\frac{\xi }{r},\) with \(T_{2}^{2}=0\) where our labeling of coordinates is \(x^{\mu }=\left( t,r,\theta \right) .\) Compared with the energy-momentum of the scalar and electromagnetic sources, which are of the order \(\frac{1}{r^{2}}\) in \(2\,+\,1\) dimensions, the order \(\frac{1}{r}\) for a string cloud may play an important role. Briefly the singularity at \(r=0\) is weaker in comparison with different sources. This forms the motivation for us to conduct the present study. We note that our cloud of strings is reminiscent of the wormhole “fur coat” model in the 5D Reissner–Nordström black hole case [40].

Such a cloud of 1-dimensional strings plays the role of particles in analogy with 1-dimensional gas atoms. The spatial geometry is confined to the polar plane with the cyclic angular coordinate. With the addition of a time variable the sheet description of the string becomes more evident. The strings are open, originating at the singular origin and extending to infinity, vanishing with \(r\rightarrow \infty .\) Thus, for \(r\rightarrow \infty \) our model reduces to the source-free (vacuum) \(f\left( R\right) \) model, which derives its power from the curvature of geometry. For \(\xi =0\) in \(f\left( R\right) =R\) model the spacetime is automatically flat unless supplemented by other sources. In \(f\left( R\right) \) gravity, on the other hand, even though we can take \(\xi =0\) we have still room for a non-flat metric albeit this may not be a black hole.

We investigate the field equations of \(f\left( R\right) \) gravity in the presence of a string cloud. In general, these are highly non-linear differential equations but owing to the simplicity of our source and the \( 2+1\) dimensions we are fortunate to obtain a large class of exact solutions. For a particular choice of the parameter n our solution can be interpreted as black holes, while for other choices it corresponds to cosmological models.

2 String-cloud source in \(f\left( R\right) =R^{n}\) gravity

Let us start with the action of the \(2+1\)-dimensional \(f\left( R\right) -\) gravity coupled to the cloud of strings,

$$\begin{aligned} I=\frac{1}{16\pi G}\int d^{3}x\sqrt{-g}f\left( R\right) +I_{S} \end{aligned}$$
(1)

in which \(f\left( R\right) =R^{n}\) is a function of the Ricci scalar R,  n is a real constant, and

$$\begin{aligned} I_{S}=\int _{\Sigma }m\sqrt{h}d\lambda ^{0}d\lambda ^{1} \end{aligned}$$
(2)

where \(\lambda ^{A}\), \((A=0,1)\) are the string parameters. The world-sheet bivector is defined by

$$\begin{aligned} \sum \nolimits ^{\mu \nu }=\epsilon ^{AB}\frac{\partial x^{\mu }}{\partial h^{A}}\frac{\partial x^{\nu }}{\partial h^{B}}, \end{aligned}$$
(3)

in which \(\epsilon ^{01}=1=-\epsilon ^{10}\) is the 2-dimensional Levi-Civita symbol. Note that the string metric has the line element

$$\begin{aligned} \mathrm{d}s_{s}^{2}=h_{AB}\mathrm{d}h^{A}\mathrm{d}h^{B}. \end{aligned}$$
(4)

Accordingly the corresponding energy-momentum tensor of the string cloud is

$$\begin{aligned} T^{\mu \nu }=\rho \frac{\sum \nolimits ^{\mu \alpha }\sum \nolimits _{\alpha }^{\nu }}{\sqrt{-h}} \end{aligned}$$
(5)

where \(\rho \) is the energy-density and \(h=\det \left( h_{AB}\right) \) refers to the world sheet of the string. The latter expression for \(T^{\mu \nu }\) is meaningful as long as \(h<0.\)

Variation of the action I with respect to \(g_{\mu \nu }\) provides the field equations (in a metric formalism),

$$\begin{aligned} \frac{\mathrm{d}f}{\mathrm{d}R}R_{\mu }^{\nu }-\frac{1}{2}f\delta _{\mu }^{\nu }-\nabla ^{\nu }\nabla _{\mu }\frac{\mathrm{d}f}{\mathrm{d}R}+\delta _{\mu }^{\nu }\square \frac{\mathrm{d}f}{\mathrm{d}R} =T_{\mu }^{\nu } \end{aligned}$$
(6)

in which \(\square \) is the covariant Laplacian and

$$\begin{aligned} T_{\mu }^{\nu }=\frac{\xi }{r}\mathrm{diag}.\left[ 1,1,0\right] \end{aligned}$$
(7)

is the energy-momentum tensor of the cloud of strings in which \(\xi \) is a real constant. The static and circular symmetric line element is set to be

$$\begin{aligned} \mathrm{d}s^{2}=-U\left( r\right) \mathrm{d}t^{2}+\frac{1}{V\left( r\right) } \mathrm{d}r^{2}+r^{2}\mathrm{d}\theta ^{2} \end{aligned}$$
(8)

with two unknown functions \(U\left( r\right) \) and \(V\left( r\right) .\) The field equations explicitly written are

$$\begin{aligned} \frac{\mathrm{d}f}{\mathrm{d}R}R_{t}^{t}-\frac{f}{2}+V\left( R^{\prime 2}\frac{\mathrm{d}^{3}f}{\mathrm{d}R^{3}} \frac{\mathrm{d}^{2}f}{\mathrm{d}R^{2}}R^{\prime \prime }\right) \nonumber \\ +\left( \frac{V^{\prime }}{2}+\frac{V}{r}\right) R^{\prime }\frac{\mathrm{d}^{2}f}{ \mathrm{d}R^{2}}=\frac{\xi }{r}, \end{aligned}$$
(9)
$$\begin{aligned} \frac{\mathrm{d}f}{\mathrm{d}R}R_{r}^{r}-\frac{f}{2}+\left( \frac{VU^{\prime }}{2U}+\frac{V}{r} \right) R^{\prime }\frac{\mathrm{d}^{2}f}{\mathrm{d}R^{2}}=\frac{\xi }{r} \end{aligned}$$
(10)

and

$$\begin{aligned} \frac{\mathrm{d}f}{\mathrm{d}R}R_{\theta }^{\theta }-\frac{f}{2}+V\left( R^{\prime 2}\frac{ \mathrm{d}^{3}f}{\mathrm{d}R^{3}}+\frac{\mathrm{d}^{2}f}{\mathrm{d}R^{2}}R^{\prime \prime }\right) \nonumber \\ +\left( \frac{VU^{\prime }}{2U}+\frac{V^{\prime }}{2}\right) R^{\prime }\frac{ \mathrm{d}^{2}f}{\mathrm{d}R^{2}}=0 \end{aligned}$$
(11)

in which

$$\begin{aligned} R_{t}^{t}=-\frac{\left[ V^{\prime }U^{\prime }Ur+2VU^{\prime \prime }Ur-VU^{\prime 2}r+2VU^{\prime }U\right] }{4rU^{2}}, \end{aligned}$$
(12)
$$\begin{aligned} R_{r}^{r}=-\frac{\left[ V^{\prime }U^{\prime }Ur+2VU^{\prime \prime }Ur-VU^{\prime 2}r+2V^{\prime }U^{2}\right] }{4rU^{2}} \end{aligned}$$
(13)

and

$$\begin{aligned} R_{\theta }^{\theta }=-\frac{\left( rVU^{\prime }+rUV^{\prime }\right) }{ 2r^{2}U}. \end{aligned}$$
(14)

Note that a prime stands for the derivative with respect to r. A set of solutions to the above field equations are given by

$$\begin{aligned} U\left( r\right) =r^{2\left( n-1\right) }\left( C-\frac{2n^{2}\xi r^{\frac{ 1-2n+2n^{2}}{n}}}{\alpha \left( 1-2n+2n^{2}\right) \left( 4n^{2}-6n+1\right) }\right) \nonumber \\ \end{aligned}$$
(15)

and

$$\begin{aligned} V\left( r\right) =r^{\frac{2\left( 1-n\right) \left( 2n-1\right) }{n} }U\left( r\right) , \end{aligned}$$
(16)

in which C is an integration constant and

$$\begin{aligned} \alpha ^{n}=n^{n}\left( \frac{4n^{2}-6n+1}{4\left( 2n-1\right) \xi }\right) ^{1-n}. \end{aligned}$$
(17)

To complete the set of solutions we provide also the explicit form of the Ricci scalar R, which reads

$$\begin{aligned} R=\frac{4\xi n\left( 2n-1\right) }{\left( 4n^{2}-6n+1\right) \alpha r^{\frac{ 1}{n}}}. \end{aligned}$$
(18)

Let us note that \(n\ne 1/2\) is a real constant which must exclude also the values \(\frac{3\pm \sqrt{5}}{4}\) since they are the roots of the denominator of R.

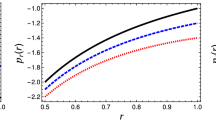
We would like to add also that, due to the arbitrary values for n and \(\xi \), our solution is a three parameter solution. For any specific value of n one has to choose an appropriate sign for \(\xi \), for which in some cases both signs may be acceptable. Setting n and the sign of \(\xi \) gives us an equation for \(\alpha \) given by (17). Depending on the number of real solutions this equation may admit, we will get different metric functions. For instance let us consider \(n=2.\) In this case one finds \(\alpha ^{2}=4\left( \frac{ 12\xi }{5}\right) \), which imposes \(\xi >0\), and consequently there are two solutions for \(\alpha \), given by \(\alpha =\pm 2\sqrt{\frac{12\xi }{5}}.\) For positive/negative \(\alpha \) one finds

$$\begin{aligned} U_{\pm }\left( r\right) =r^{2}\left( C\mp \frac{2\sqrt{15\xi }r^{\frac{5}{2}} }{75}\right) . \end{aligned}$$
(19)

Here clearly \(U_{-}\left( r\right) \) is a black hole solution considering \( C<0\) and therefore we may rewrite the metric as

$$\begin{aligned} U_{-}\left( r\right) =r^{2}\left| C\right| \left( \left( \frac{r}{ r_{h}}\right) ^{\frac{5}{2}}-1\right) , \end{aligned}$$
(20)

in which the horizon is located at

$$\begin{aligned} r_{h}=\left( \frac{75\left| C\right| }{2\sqrt{15\xi }}\right) ^{ \frac{2}{5}}. \end{aligned}$$
(21)

In general, for \(n\ge 2\) an even integer number the picture is the same as \( n=2\) i.e., \(\alpha =\pm n\left( \frac{4n^{2}-6n+1}{4\left( 2n-1\right) \xi } \right) ^{\frac{1-n}{n}}\) with \(\xi >0.\) The general solution hence can be cast as a black hole solution provided \(C<0\) and negative \(\alpha \) such that

$$\begin{aligned} U_{-}\left( r\right) =r^{2\left( n-1\right) }\left| C\right| \left( \left( \frac{r}{r_{h}}\right) ^{\frac{1-2n+2n^{2}}{n}}-1\right) \end{aligned}$$
(22)

in which the location of the horizon is given by

$$\begin{aligned} r_{h}=\left( \frac{2\left( 1-2n+2n^{2}\right) \left( 2n-1\right) \left| C\right| }{n\left( \frac{4\left( 2n-1\right) }{4n^{2}-6n+1}\xi \right) ^{ \frac{1}{n}}}\right) ^{\frac{n}{1-2n+2n^{2}}}. \end{aligned}$$
(23)

For odd integers and other real numbers as we mentioned above, one must carefully go through any individual case and find the final form of the spacetime. Ultimately it gives either a black hole solution, as we mentioned above, or a particle solution. For instance, in the case of \(n=2\) the positive branch, i.e., \(U_{+}\left( r\right) \) with positive C, the solution represents a particle solution [41].

2.1 \(f\left( R\right) =R\) with geodesics

In the second example we consider \(n=1\), which simply gives the Einstein R gravity coupled to the cloud of strings minimally. Let us note that this solution was found first by Bose et al. in [42]. The solution becomes

$$\begin{aligned} U\left( r\right) =V\left( r\right) =-M+2\xi r \end{aligned}$$
(24)

and

$$\begin{aligned} R=-\frac{4\xi }{r}. \end{aligned}$$
(25)

As one observes, there is no restriction on the sign of \(\xi \) and therefore the solution represents either a singular black hole or a naked singularity. In the case of the black hole the singularity is hidden behind an event horizon located at

$$\begin{aligned} r_{h}=\frac{M}{2\xi }. \end{aligned}$$
(26)

2.1.1 Geodesics confinement for \(f\left( R\right) =R\)

The black hole solution in R gravity given by (24) is rather interesting if we assume \(M,\xi >0\). In this section we investigate the null and timelike geodesics of this solution. Let us start with the Lagrangian

$$\begin{aligned} L=\frac{1}{2}g_{\mu \nu }\frac{\mathrm{d}x^{\mu }}{\mathrm{d}\lambda }\frac{\mathrm{d}x^{\nu }}{ \mathrm{d}\lambda } \end{aligned}$$
(27)

in which \(\lambda \) is an arbitrary parameter. We also introduce the null (\( \epsilon =0\)) and timelike (\(\epsilon =1\)) geodesics by

$$\begin{aligned} g_{\mu \nu }\frac{\mathrm{d}x^{\mu }}{\mathrm{d}\lambda }\frac{\mathrm{d}x^{\nu }}{\mathrm{d}\lambda }=-\epsilon . \end{aligned}$$
(28)

The line element

$$\begin{aligned} \mathrm{d}s^{2}=-U\mathrm{d}t^{2}+\frac{\mathrm{d}r^{2}}{U}+r^{2}\mathrm{d}\theta ^{2} \end{aligned}$$
(29)

in which \(U=-M+2\xi r\) admits two Killing vectors, i.e., \(\partial _{t}\) and \(\partial _{\theta }\) corresponding to the conserved energy and angular momentum given by

$$\begin{aligned} E=-U\frac{\mathrm{d}t}{\mathrm{d}\lambda } \end{aligned}$$
(30)

and

$$\begin{aligned} \ell =r^{2}\frac{\mathrm{d}\theta }{\mathrm{d}\lambda }. \end{aligned}$$
(31)

Considering these one finds the only equation to be solved as

$$\begin{aligned} \left( \frac{\mathrm{d}r}{\mathrm{d}\lambda }\right) ^{2}+U\left( \epsilon +\frac{\ell ^{2}}{ r^{2}}\right) =E^{2}. \end{aligned}$$
(32)

For the null radial geodesics with \(\epsilon =\ell ^{2}=0\) one finds

$$\begin{aligned} r_{\pm }=r_{0}e^{\pm 2\xi \left( t-t_{0}\right) }+r_{h}\left( 1-e^{\pm 2\xi \left( t-t_{0}\right) }\right) \end{aligned}$$
(33)

in which \(r_{0}\) and \(t_{0}\) are the initial location and time of the null particle with respect to a distant observer. The sign \(\pm \) stands for the direction of the initial velocity, positive for outward and negative for inward motion. As one can see

$$\begin{aligned} \frac{\mathrm{d}r_{\pm }}{\mathrm{d}t}=\pm 2\xi \left( r_{\pm }-r_{h}\right) \end{aligned}$$
(34)

and

$$\begin{aligned} \lim _{t\rightarrow \infty }r_{+}= & {} \infty \nonumber \\ \lim _{t\rightarrow \infty }\frac{\mathrm{d}r_{+}}{\mathrm{d}t}= & {} \infty , \end{aligned}$$
(35)

while

$$\begin{aligned} \lim _{t\rightarrow \infty }r_{-}= & {} r_{h}. \nonumber \\ \lim _{t\rightarrow \infty }\frac{\mathrm{d}r_{-}}{\mathrm{d}t}= & {} 0. \end{aligned}$$
(36)

In the case of timelike radial geodesics with \(\epsilon =1,\ell ^{2}=0\) one finds (for \(\lambda =\tau \))

$$\begin{aligned} r=r_{0}-\frac{1}{2}\xi \tau ^{2}, \end{aligned}$$
(37)

in which \(\tau \) is the proper time and \(r_{0}\) is the initial position of the particle. To reach the horizon, the proper time needed by the particle is just \(\tau _{h}=\sqrt{\frac{2\left( r_{0}-r_{h}\right) }{\xi }}\). In terms of the coordinate time t the equation of motion becomes

$$\begin{aligned} \left( \frac{\mathrm{d}r}{\mathrm{d}t}\right) ^{2}=U^{2}\left( 1-\frac{U}{E^{2}}\right) . \end{aligned}$$
(38)

If we consider the particle to be at rest at \(t=t_{0}\) we find \(E^{2}=M\left( \frac{r_{0}}{r_{h}}-1\right) \), which consequently implies

$$\begin{aligned} \left( \frac{\mathrm{d}r}{\mathrm{d}t}\right) ^{2}=4\xi ^{2}\left( r-r_{h}\right) ^{2}\left( \frac{r_{0}-r}{r_{0}-r_{h}}\right) , \end{aligned}$$
(39)

which admits the solution

$$\begin{aligned} r=r_{0}-\left( r_{0}-r_{h}\right) \tanh ^{2}\left[ \xi \left( t-t_{0}\right) \right] . \end{aligned}$$
(40)

Clearly the particle is attracted toward the black hole and when \( t\rightarrow \infty \) the limit goes to \(r=r_{h}.\) This time is not comparable with the proper time interval needed for the particle to cross the horizon.

In circular motion for a null particle one finds the only unstable orbit is located at \(r_{c}=2r_{h}\) (photon circle’s radius) at which for the null particle one finds

$$\begin{aligned} \frac{E^{2}}{\ell ^{2}}=\frac{\xi }{2r_{h}}. \end{aligned}$$
(41)

This can easily be justified from Eq. (32), by considering the potential of the particle given by

$$\begin{aligned} V\left( r\right) =U\left( r\right) \left( \epsilon +\frac{\ell ^{2}}{r^{2}} \right) -E^{2} \end{aligned}$$
(42)

whose derivative satisfies \(\frac{\mathrm{d}V}{\mathrm{d}r}=0\), at \(r=r_{c},\) and \(\epsilon =0\) for the null geodesics. For the timelike geodesics a similar analysis applies with the substitution \(\epsilon =1.\)

Furthermore, for a timelike particle we find the stable orbit at \(r=r_{c}\) where the angular momentum and the energy of the particle are given by

$$\begin{aligned} \ell ^{2}=\frac{r_{c}^{3}}{r_{c}-2r_{h}} \end{aligned}$$
(43)

and

$$\begin{aligned} E^{2}=4\xi \frac{\left( r_{c}-r_{h}\right) r_{h}}{\left( r_{c}-2r_{h}\right) }. \end{aligned}$$
(44)

We see clearly that \(r_{c}>2r_{h}\), which is outside a photon circle around the black hole.

2.1.2 Generalization to \(f\left( R\right) =R^{n}\) with n an even integer and \(n\ge 2\)

The geodesic analysis given in the previous part can be generalized with \( f\left( R\right) =R^{n}.\) As we are interested in the black hole geodesics, we impose n to be even integer bigger than 1, i.e., \(n\ge 2.\) In order to keep the mathematical expression analytic we only consider the radial, null geodesics. Accordingly one finds from the Euler–Lagrange equations

$$\begin{aligned} \pm \frac{\mathrm{d}r}{\mathrm{d}\lambda }=Er^{\frac{\left( 1-n\right) \left( 2n-1\right) }{n}} \end{aligned}$$
(45)

and

$$\begin{aligned} \pm \frac{\mathrm{d}t}{\mathrm{d}\lambda }=\frac{E}{U}, \end{aligned}$$
(46)

in which E is the energy of the particle and \(\lambda \) is an affine parameter. Combining these two equations we find

$$\begin{aligned} \frac{\mathrm{d}r}{\mathrm{d}t}=\pm r^{\frac{\left( 1-n\right) \left( 2n-1\right) }{n}}U \end{aligned}$$
(47)

with its integral expression in the form

$$\begin{aligned} \int _{r_{0}}^{r}\frac{r^{\frac{\left( n-1\right) \left( 2n-1\right) }{n}}\mathrm{d}r}{ U}=\pm \left( t-t_{0}\right) \end{aligned}$$
(48)

where \(t_{0}\) is the initial time when the particle is located at \( r_{0}>r_{h}\) and \(r_{h}\) is the event horizon. Plugging (22) into the latter equation we reexpress

$$\begin{aligned} \int _{r_{0}}^{r}\frac{r^{\frac{1-n}{n}}\mathrm{d}r}{\left| C\right| \left( \left( \frac{r}{r_{h}}\right) ^{\frac{1-2n+2n^{2}}{n}}-1\right) }=\pm \left( t-t_{0}\right) . \end{aligned}$$
(49)

Obviously an exact integral of this expression is out of our reach. Even for particular values of n we have to appeal to the asymptotic behavior. Considering r to be large i.e., \(\frac{r_{h}}{r}\ll 1\) and \(n>0\), one approximately finds

$$\begin{aligned} r^{2\left( 1-n\right) }-r_{0}^{2\left( 1-n\right) }\simeq \mp \omega \left( t-t_{0}\right) \end{aligned}$$
(50)

in which the constant \(\omega \) is given by

$$\begin{aligned} \omega =2\left( n-1\right) \left| C\right| \left( \frac{1}{r_{h}} \right) ^{\frac{1-2n+2n^{2}}{n}}. \end{aligned}$$
(51)

Let us add that considering \(\frac{r_{h}}{r}\ll 1\) in (49) implicitly implies that the initial location of the particle is far from the horizon, i.e., \( \frac{r_{h}}{r_{0}}\ll 1\) too. The latter equation implies that at least for this specific choice the motion is confined.

3 Conclusion

In search of alternative black holes to the BTZ in \(2+1\) dimensions a particular case was considered in Einstein’s theory of \(f\left( R\right) =R\) in which the source is a cloud of strings [42]. Projected in the polar plane the string can be considered as radial lines originating at the origin and extending in radial in/out directions. This excludes the possibility of a closed string in such a geometry. The advantage of such a choice of source becomes evident when substituted into the complicated \(f\left( R\right) =R^{n}\) gravity which we consider here. In other words our geometry is powered by such a cloud of strings in the \(f\left( R\right) =R^{n}\) gravity with the energy-momentum tensor \(T_{0}^{0}=T_{1}^{1}=\frac{\xi }{r}\) and \( T_{2}^{2}=0\) with \(\xi =\)constant. Obviously this satisfies the null energy conditions. Although n can be arbitrary in principle there are restrictions on the choice of n for a meaningful expression. For instance, \(n=\frac{1}{2}\) and \(n=\frac{3\pm \sqrt{5}}{4}\) are to be excluded in the class of metric solutions. Depending on the other values of n we obtain an infinite class of possible metrics that describe black holes/naked singularities in \(2+1\)-dimensional \(f\left( R\right) =R^{n}\) gravity theory. An interesting physical conclusion to be drawn from these solutions is the role that the power n plays in the confinement of (especially) null geodesics. Although the most general analytic integration of the geodesics is lacking we obtain an approximate connection between the parameter n and the confinement of the null geodesics for n an even integer greater than 1. Whether a similar relation occurs in higher dimensions \((D>3)\) for a cloud of strings as source remains to be seen.