Abstract
We construct a toy model for compact stars based on the Finslerian structure of spacetime. By assuming a particular mass function, we find an exact solution of the Finsler–Einstein field equations with an anisotropic matter distribution. The solutions are revealed to be physically interesting and pertinent for the explanation of compact stars.
Similar content being viewed by others
1 Introduction
Spherically symmetric spacetime related astrophysical problems have been always interesting to mathematician as well as physicists. This is because of the fact that phenomena such as black holes, wormholes and compact stars (starting from dwarf stars via neutron stars to quark/strange stars through the vigorous process of gravitational collapse) have been originated in the class of system with spherical symmetry.
After the monumental construction of Einstein’s general theory of relativity in the period 1907–1915 [1], numerous investigators have been started studying relativistic stellar models with various aspects of physical reality. The investigation of the exact solutions recounting static isotropic and anisotropic astrophysical objects has continuously fascinated scientists with growing interest and attraction. However, it has till now been observed that most of the exact interior solutions (both isotropic and anisotropic) of the gravitational field equations do not fulfill, in general, the required physical conditions of the stellar systems.
The existence of massive compact stellar system was first proposed by Baade and Zwicky in 1934 [2] when they argued that supernova may yield a very small and dense star consisting primarily of neutrons. It eventually came in to reality by the discovery of pulsar, a highly magnetized and rotating neutron star, in 1967 by Bell and Hewish [3, 4]. There after the theoretical investigation of compact stars became fundamental area of importance in astrophysics. However, for modeling a compact star emphasis has been given in general on the homogeneity of the spherically symmetric matter distribution and thus assumption was always valid for the perfect fluid obeying the Tolman–Oppenheimer–Volkoff (TOV) equation.
It was Ruderman [5] who first argued that the nuclear matter density (\(\rho \sim 10^{15}\) gm/cc), which is expected at the core of the compact terrestrial object, becomes very much anisotropic. In such case of anisotropy the pressure inside the fluid sphere can specifically be decomposed into two parts: radial pressure and the transverse pressure, where they are orthogonal to each other. Therefore it is quite reasonable to consider pressure anisotropy in any compact stellar model. In this context it can be noted that Gokhroo and Mehra [6] have shown that in case of anisotropic fluid the existence of repulsive force helps to construct compact objects.
Other than the above mentioned ultra density [5] anisotropy may occur for different reasons in the compact stellar system. Kippenhahn and Weigert [7] have argued that anisotropy could be introduced due to the existence of solid core or for the presence of type 3A-superfluid. Some other reasonable causes for arising anisotropy are: different kind of phase transitions [8], pion condensation [9], effects of slow rotation in a star [10], etc. However, Bowers and Liang [11] indicated that anisotropy might have non-negligible effects on such parameters like equilibrium mass and surface redshift. In connection to pressure anisotropy inside a compact star several recent theoretical investigations are available in the literature [12–19]. However, there is an exhaustive review on the subject of anisotropic fluids by Herrera and Santos [20] which provides almost all references until 1997 and hence may be looked at for further information.
Several major characteristics of compact stars established by the present day observations have been tackled by Einstein’s general theory of relativity based on Riemannian geometry. Ever since the beginning of the general theory of relativity, there has also been considerable interest in Alternative theories of gravitation. One of the most stimulating alterations of general relativity is that proposed by Finsler [21].
The first self-consistent Finsler geometry model was studied by Cartan [22] in 1935 and the Einstein–Finsler equations for the Cartan d-connection were introduced in 1950 [23]. Latter on, there were studies on various models of Finsler geometry and certain applications to physics [21, 24]. The first problem of those original works was related to the Finsler connections (due to Chern–Rund and/or Berwald) with non-metricity fields (see details and critics in [24, 25]). The second and third conceptual and technical problems were related to the facts that the geometric constructions were in the bulk for local Euclidean signatures. However, in some cases Finsler pseudo-Riemannian configurations were considered but researchers were not able to find out any exact solution.
In a self-consistent manner and related to standard theories, relativistic models of Finsler gravity and generalizations were constructed in the beginning of 1996 [26, 27], when Finsler gravity and locally anisotropic spinors were derived in low energy limits of superstring/supergravity theories with N-connection structure (velocity type coordinates being treated as extra-dimensional ones). Using Finsler geometric methods, it was elaborated to the so-called anholonomic frame deformation method (AFDM), which allows to construct generic off-diagonal exact solutions in various modified gravity theories, including various commutative and noncommutative Finsler generalizations, and in general relativity [28–30]. In this way various classes of exact solutions for Finsler modifications of black hole, black ellipsoid/torus/brane and string configurations, locally anisotropic cosmological solutions have been constructed for the canonical d-connection and Cartan d-connections.
The Finslerian space is very suitable for studying anisotropic nature of spacetime (it’s mathematical aspects can be obtained in detail in Sect. 2). Basically this space is a generalization of Riemannian space and has been studied in several past years extensively in connection to astrophysical problems, e.g. Lämmerzahl et al. [31] have investigated observable effects in a class of spherically symmetric static Finslerian spacetime whereas Pavlov [32] searches for applicable character of the Finslerian spacetime by raising the question “Could kinematical effects in the CMB prove Finsler character of the space–time?” Another astrophysics oriented application of the Finslerian spacetime can be noted through the work of Vacaru [33] where the author has studied Finsler black holes induced by noncommutative anholonomic distributions in the Einstein gravity.
Therefore, in the present investigation our sole aim is to construct a toy model for compact stars under the Finslerian spacetime which can provide justification of several physical features of the stellar system. The outline of the study is as follows: in Sect. 2 the basic equations based on the formalism of the Finslerian geometry are discussed whereas a set of specific solutions for compact star under Finslerian spacetime has been produced in Sect. 3. The exterior spacetime and junction conditions are sought for in Sect. 4 in connection to certain observed compact stars. In Sect. 5, through several subsections, we discuss in a length various physical properties of the model. We pass some concluding remarks in Sect. 6 for the status of the present model as well as future plans of the work to be pursued. An Appendix has been incorporated for justification as well as clarification of some of the assumptions in mathematical part of the formulation.
2 The basic equations based on the formalism of the Finslerian geometry
Usually, the Finslerian geometry can be constructed from the so called Finsler structure F which obeys the property
for all \( \mu > 0\), where \( x \in M \) represents position and \( y = \frac{\mathrm{d}x}{\mathrm{d}t}\) represents velocity. The Finslerian metric is given as [34]
It is to be noted here that a Finslerian metric coincides with Riemannian, if \(F^2\) is a quadratic function of y.
The standard geodesic equation in the Finsler manifold can be expressed as
where
is called geodesic spray coefficients. The geodesic equation (2) indicates that the Finslerian structure F is constant along the geodesic.
The invariant quantity, Ricci scalar, in Finsler geometry is given as
where \(R^\mu _\nu =R^\mu _{\lambda \nu \rho }y^\lambda y^\rho /F^2\).
Here, \(R^\mu _{\lambda \nu \rho }\) depends on connections whereas \(R^\mu _\mu \) does not rather it depends only on the Finsler structure F and is insensitive to connections.
Let us consider the Finsler structure is of the form [34]
Then, the Finsler metric can be obtained as
where the metric \(\bar{g}_{ij}\) and its reverse are derived from \(\bar{F}\) and the index i, j run over the angular coordinate \(\theta ,\phi \).
Substituting the Finsler structure (5) into Eq. (3), we find
where the prime denotes the derivative with respect to r, and the \(\bar{G}\) is the geodesic spray coefficients derived by \(\bar{F}\). Plugging the geodesic coefficient (8), (9), (10) and (11) into the formula of Ricci scaler (4), we obtain
where \(\bar{\mathrm{R}}\mathrm{ic}\) denotes the Ricci scalar of the Finsler structure \(\bar{F}\).
Now, we are in a position to write the self-consistent gravitational field equation in Finsler spacetime. In a pioneering work Akbar-Zadeh [35] first introduced the notion of Ricci tensor in the Finsler geometry as
Here the scalar curvature in the Finsler geometry is defined as \(S=g^{\mu \nu }\mathrm{Ric}_{\mu \nu }\). Therefore, the modified Einstein tensor in the Finsler spacetime takes the following form as
Using equation of Ricci scalar (12), one can obtain from (13), the Ricci tensors in Finsler geometry. This immediately yield the Einstein tensors in the Finsler geometry (note that \(\bar{F}\) is two dimensional Finsler spacetime with constant flag curvature \(\lambda \)) as follows:
It has been shown by Li and Chang [34] that the covariant derivative of Einstein tensors in Finsler geometry \(G_{\mu \nu }\) vanishes i.e. covariant conserve properties of the tensor \(G_{\mu \nu }\) indeed satisfy.
Following the notion of general relativity, one can write the gravitational field equations in the given Finsler spacetime as (see the Appendix for justification)
where \(T^\mu _\nu \) is the energy–momentum tensor.
Note that the volume of Riemannian geometry is not equal to that of the Finsler space, therefore, it is safe to use \(4\pi _F\) for expressing the volume of \(\bar{F}\) in the field equation.
The matter distribution of a compact star is still a challenging issue to the physicists and therefore, as our target is to find the interior of a compact star, we assume the general anisotropic energy–momentum tensor [36] as follows:
where \(u^{\mu }u_{\mu } = - \eta ^{\mu }\eta _{\mu } = 1\), \(p_t\) and \(p_r\) are transverse and radial pressures, respectively.
Using the above energy-momentum tensor (19), one can write the gravitational field equations in the Riemannian geometry as
Using Eq. (20) we get the value of A, which is given below as
where m(r) is the mass contained in a sphere of radius r defined by
3 The model solution for compact star under the Finslerian spacetime
To construct a physically viable model as well as to make the above set of equations solvable, we choose the mass function m(r) in a particular form that has been considered by several authors for studying isotropic fluid spheres [37], dark energy stars [38] and anisotropic stars [39, 40] as
where two constants a, b are positive. The motivation of this particular choice of mass function lies on the fact that it represents a monotonic decreasing energy-density in the interior of the star. Also it gives the energy-density to be finite at the origin \(r = 0\). The constants may be determined from the boundary conditions.
Putting the expression of m(r) in Eq. (24), we get
To determine the unknown metric potentials and physical parameters, we use the usual equation of state
where the equation of state parameter \(\omega \) has the constrain \(0<\omega <1\). Usually, this equation is used for a spatially homogeneous cosmic fluid, however, it can be extended to inhomogeneous spherically symmetric spacetime, by assuming that the radial pressure follows the above equation of state. The transverse pressure may be obtained from the field equations.
Plugging Eqs. (26) and (27) in Eqs. (20)–(23), we get the explicit expressions of the unknowns in the following forms:
where \(B_0\) is an integration constant and without any loss of generality, one can take it as unity.
The radial and tangential pressures are given by
Note from the above expressions for the radial and tangential pressures that the solutions obtained here are regular at the center. Now, the central density can be obtained as
The anisotropy of pressures dies out at the center and hence we have
One can notice that as we match our interior solution with external vacuum solution (pressure zero) at the boundary, then, at the boundary, all the components of the physical parameters are continuous along the tangential direction (i.e. zero pressure), but in normal direction it may not be continuous. Therefore, at the boundary, pressure may zero along tangential direction, but in normal direction it may not be zero. So, non-zero pressure at the boundary is not unrealistic.
4 Exterior spacetime and junction condition
Now, we match the interior spacetime to the exterior vacuum solution at the surface with the junction radius R. The exterior vacuum spacetime in the Finslerian spacetime is given by the metric [34]
Across the boundary surface \(r= R\) between the interior and the exterior regions of the star, the metric coefficients \(g_{tt}\) and \(g_{rr}\) both are continuous. This yields the following results:
The above two equations contain four unknown quantities, viz., \(a,~b,~\lambda , ~\omega \). Equation (32) yields the unknown b in terms of central density. Also from the total mass of star \(m(r=R) =M =\frac{bR^3}{2(1+aR^2)} \), we can find out the constant a in terms of the total mass M, radius R and central density. Finally, Eqs. (35) and (36) yield the unknowns - the flag curvature \(\lambda \) and the equation of state parameter \(\omega \) in terms of the total mass M, radius R and central density. The values of the constants a, b for different strange star candidates are given in Table 1. Note that for matching we have used four constraint equations with four unknown and all the unknown parameters are found in terms of R and M. For the use of continuity of \( \frac{\mathrm{d}g_{tt} }{\mathrm{d}r}\), we will get an extra equation which gives a restriction equation of M and R. As we have used real parameters of mass and radius of different compact stars like \(PSR~J1614-2230\), etc., we avoid this continuity of \(\frac{\mathrm{d}g_{tt }}{\mathrm{d}r}\).
5 Physical features of the compact star model
5.1 Mass–Radius relation
The study of redshift of light emitted at the surface of the compact objects is important to get observational evidence of anisotropies in the internal pressure distribution. Before finding out the redshift, we give our attention to the basic requirement of the model that whether matter distribution will follow the Buchdahl [41] maximum allowable mass–radius ratio limit or not. We have already found out the mass of the star which has been given in Eq. (24).
The compactness of the star can be expressed as
and the corresponding surface redshift can be obtained as
The variation of mass, compactness factor and redshift are shown in Fig. 1 for different strange star candidates for a fixed value of \(\lambda =0.01\) whereas the maximum mass, compactness factor and redshift are shown in Table 2. From this Table 2 we have found out that
Therefore, one can note that the Buchdahl limit (which is equivalent to \(Z_\mathrm{s} \le 2\), the upper bound of a compressible fluid star) has been satisfied in our model and hence it is physically acceptable.
The surface redshift \(Z_\mathrm{s}\) can be measured from the X-ray spectrum which gives the compactness of the star. In our study, the high redshift (\(0.36{-}0.49\)) are consistent with strange stars which have mass–radius ratio higher than neutron stars (\(Z_\mathrm{s} \le 0.9\)) [42].
Variation of the square of the radial velocity vs radial coordinate (upper left), square of the transverse velocity vs radial coordinate (upper right) and difference between the square of the transverse velocity and square of the radial velocity vs radial coordinate (lower) are shown in the plot for the specified range of the positive flag curvature
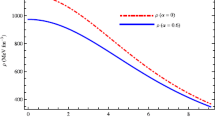
5.2 Energy conditions
Now, we verify the energy conditions, namely, the null energy condition (NEC), weak energy condition (WEC) and strong energy condition (SEC) which can be given as follows:
We plot the L.H.S of the above inequalities in Fig. 2 which shows that these inequalities hold good. This therefore confirm that our model satisfies all the energy conditions.
5.3 TOV equation
The generalized Tolman–Oppenheimer–Volkoff (TOV) equation for this system can be given by [13]
where \(M_G=M_G(r)\) is the effective gravitational mass inside a sphere of radius r given by the Tolman–Whittaker formula which can be derived from the equation
The above equation explains the equilibrium condition of the fluid sphere due to the combined effect of gravitational, hydrostatics and anisotropy forces. Equation (42) can be rewritten in the following form
where
The profiles (Fig. 3) of these force indicate that the matter distribution comprising the compact star is in equilibrium state subject to the gravitational force \(F_\mathrm{g}\), hydrostatic force \(F_\mathrm{h}\) plus another force \(F_\mathrm{a}\) due to anisotropic pressure. The first two forces are repulsive in nature due to positivity but the latter force is in attractive nature. The combined effect of these forces makes the system in a equilibrium position.
5.4 Stability
Now, we examine the stability of model. For this purpose, we employ the technique proposed by Herrera [43] which is known as cracking concept. At first, it requires that the squares of the radial and tangential sound speeds should be within the limit [0, 1]. The theorem states that one can get stable configuration if radial speed of sound is greater than that of transverse speed, i.e. \(v_\mathrm{st}^2 - v_\mathrm{sr}^2\) should be less than zero within the matter distribution.
Now, we calculate the radial speed (\(v_\mathrm{sr}\)) and transverse speed (\(v_\mathrm{st}\)) for our anisotropic model as
where
To check whether the sound speeds lie between 0 and 1 and \(v_\mathrm{st}^2 - v_\mathrm{sr}^2 <0\) we plot the radial and transverse sound speeds and squares of their difference. The Fig. 4 satisfies Herrera’s criterion and therefore, our model is quite stable one.
6 Concluding remarks
In the present investigation, we have considered anisotropic matter source for constructing a new type of solutions for compact stars. The background geometry is taken as the Finslerian structure of spacetime. It is expected that the compactness of these stars is greater than that of a neutron star. Plugging the expressions for G and c in the relevant equations, one can figure out that the value of the central density for the choices of the constant b turns out to be \(\rho _0 \propto ~ 10^{15}\) gm cm\(^{-3}\) which is in observational relevance [5, 44, 45]. This result is hopeful as far as physical aspect is concerned and may be treated as a seminal bottom line of the present study.
In this same physical point of view we have studied several other physical aspects of the model to justify validity of the solutions. The features that emerge out from the present investigation can be put forward as follows:
-
(1)
Mass–Radius relation: The surface redshift, which gives the compactness of the star, comes out to be in the range \(0.36{-}0.49\) in our study. This high redshift is consistent with strange stars which have mass–radius ratio higher than neutron stars [42]. In this connection we were also curious about the condition of Buchdahl [41] related to the maximum allowable mass–radius ratio limit. It is observed that the Buchdahl limit has been satisfied by our model.
-
(2)
Energy condition: In the present model all the energy conditions are shown to be satisfactory.
-
(3)
TOV equation: The generalized Tolman–Oppenheimer–Volkoff equation for the Finslerian system of compact star has been studied. It is observed that the combined effect of the forces in action keeps the system in static equilibrium.
-
(4)
Stability: The stability of the model has been examined by employing the cracking technique of Herrera [43]. We have shown via Fig. 4 that Herrera’s criterion satisfies which therefore indicates stability of our model. As a final comment we would like to mention that the toy model as put forward in the present study for compact stars under the Finslerian structure of spacetime are seem very promising. However, some other aspects are deemed to be performed, such as issues of formation and structure of various compact stars, before one could be confirmed about the satisfactory role of the Finslerian spacetime than that of the Riemannian geometry. Specifically several other issues as argued by Pfeifer and Wohlfarth [46] that “Finsler spacetimes are viable non-metric geometric backgrounds for physics; they guarantee well defined causality, the propagation of light on a non-trivial null structure, a clear notion of physical observers and the existence of physical field theories determining the geometry of space–time dynamically in terms of an extended gravitational field equation” can be sought for in a future study.
References
A. Pais, Subtle is the Lord: The Science and Life of Albert Einstein (Oxford University Press, Oxford, 1982)
W. Baade, F. Zwicky, Phys. Rev. 46, 76 (1934)
M.S. Longair, High Energy Astrophysics, Vol. 2 (Cambridge University, Cambridge, 1994), p. 99
P. Ghosh, Rotation and Accretion Powered Pulsars (World Scientific, Singapore, 2007), p. 2
R. Ruderman, Rev. Astr. Astrophys. 10, 427 (1972)
M.K. Gokhroo, A.L. Mehra, Gen. Relativ. Gravit. 26, 75 (1994)
R. Kippenhahn, A. Weigert, Steller Structure and Evolution (Springer, Berlin, 1990)
A.I. Sokolov, JETP 79, 1137 (1980)
R.F. Sawyer, Phys. Rev. Lett. 29, 382 (1972). (Erratum. Phys. Rev. Lett. 29, 823 (1972))
H.O. Silva et al. (2014). arXiv:1411.6286
R.L. Bowers, E.P.T. Liang, Astrophys. J. 188, 657 (1917)
L. Herrera, A. Di Prisco, J. Martin, J. Ospino, N.O. Santos, O. Troconis, Phys. Rev. D 69, 084026 (2004)
V. Varela, F. Rahaman, S. Ray, K. Chakraborty, M. Kalam, Phys. Rev. D 82, 044052 (2010)
F. Rahaman, S. Ray, A.K. Jafry, K. Chakraborty, Phys. Rev. D 82, 104055 (2010)
F. Rahaman, R. Sharma, S. Ray, R. Maulick, I. Karar, Eur. Phys. J. C 72, 2071 (2012)
F. Rahaman, R. Maulick, A.K. Yadav, S. Ray, R. Sharma, Gen. Rel. Grav. 44, 107 (2012)
M. Kalam, F. Rahaman, S. Ray, M. Hossein, I. Karar, J. Naskar, Euro. Phys. J. C 72, 2248 (2012)
Sk.M. Hossein, F. Rahaman, J. Naskar, M. Kalam, S. Ray, Int. J. Mod. Phys. D 21, 1250088 (2012)
M. Kalam, A.A. Usmani, F. Rahaman, S.M. Hossein, I. Karar, R. Sharma, Int. J. Theor. Phys. 52, 3319 (2013)
L. Herrera, N.O. Santos, Phys. Rep. 286, 53 (1997)
D. Bao, S.S. Chern, Z. Shen, An Introduction to RiemannFinsler Geometry, Graduate Texts in Mathematics (Springer, New York, 2000)
E. Cartan, Les Espaces de Finsler (Herman, Paris, 1935)
J.I. Horvth, Phys. Rev. 80, 2001 (1950)
S. Vacaru, Int. J. Mod. Phys. D 21, 1250072 (2012)
S. Vacaru, Phys. Lett. B 690, 224 (2010)
S. Vacaru, Nucl. Phys. B 434, 590 (1997)
S. Vacaru, J. Math. Phys. 37, 508 (1996)
S. Vacaru, Gen. Relativ. Gravit. 44, 1015 (2012)
S. Rajpoot, S. Vacaru, Int. J. Geom. Meth. Mod. Phys. 12, 1550102 (2015)
P. Stavrinos, S. Vacaru, Class. Quant. Gravit. 30, 055012 (2013)
C. Lämmerzahl, V. Perlick, W. Hasse, Phys. Rev. D 86, 104042 (2012)
D.G. Pavlov, AIP Conf. Proc. 1283, 180 (2010)
S.I. Vacaru, Class. Quant. Gravit. 27, 105003 (2010)
X. Li, Z. Chang, Phys. Rev. D 90, 064049 (2014)
H. Akbar-Zadeh, Acad. R. Belg. Bull. Cl. Sci. 74, 281 (1988)
F. Rahaman et al., Phys. Rev. D 82, 104055 (2010)
M.R. Finch, J.E.F. Skea, Class. Quant. Gravit. 6, 467 (1989)
F.S.N. Lobo, Class. Quant. Gravit. 23, 1525 (2006)
M.K. Mak, T. Harko, Proc. R. Soc. Lond. A 459, 393 (2003)
R. Sharma, S. Maharaj, MNRAS 375, 1265 (2007)
H.A. Buchdahl, Phys. Rev. 116, 1027 (1959)
L. Lindblom, Astrophys. J. 278, 364 (1984)
L. Herrera, Phys. Lett. A 165, 206 (1992)
N.K. Glendenning, Compact Stars: Nuclear Physics, Particle Physics and General Relativity (Springer, New York, 1997), p. 70
M. Herjog, F.K. Röpke, Phys. Rev. D 84, 083002 (2011)
C. Pfeifer, M. Wohlfarth, Proceedings of the MG13 Meeting on General Relativity (Stockholm University, Sweden, 2012). doi:10.1142/9789814623995_0094
X. Li, S. Wang, Z. Chang (2013). arXiv:1309.1758
C. Pfeifer, M.N.R. Wohlfarth, Phys. Rev. D 85, 064009 (2012)
Acknowledgments
FR and SR are thankful to the Inter-University Centre for Astronomy and Astrophysics (IUCAA), India for providing Visiting Associateship under which a part of this work was carried out. FR is also grateful to DST, Govt. of India for financial support under PURSE programme. We are also grateful to the referee for his valuable suggestions which have enabled us to improve the manuscript substantially.
Author information
Authors and Affiliations
Corresponding author
Appendix
Appendix
Let us choose \(\bar{F^2}\) in the following form
That is
One can find from \(\bar{F^2}\)
Hence, one obtains
Now, coefficient of \(y^\phi y^\theta =0\) iff, f is independent of \(\phi \) i.e.
where the coefficient of \(y^\theta y^\theta \) & \(y^\phi y^\phi \) are non zero.
Therefore
Hence
where \(\lambda \) may be a constant or a function of \(\theta \).
Putting \(\frac{1}{f}\left( \frac{\partial f}{\partial \theta }\right) =T(\theta )\), the above equation yields
For constant \(\lambda \), one can get Finsler structure \(\bar{F^2}\) as
where A may be taken as 1.
Now, the Finsler structure takes the form
where \(\chi (\theta ) = \sin ^2 \theta - \sin ^2(\sqrt{\lambda } \theta )\).
Thus
Let \(b_\phi = r\sqrt{ \chi (\theta )} \), then
where,
Finally, we have
Hence, F is the metric of \((\alpha , \beta )\)-Finsler space.
The killing equation \(K_V(F) =0 \) in the Finsler space can be obtained by considering the isometric transformations of Finsler structure [47]. One can investigate the Killing vectors of \((\alpha , \beta )\)-Finsler space. The Killing equations for this class of Finsler space is given as
where
Here \(``\mid \)” represents the covariant derivative with respect to the Riemannian metric \(\alpha \). For the present case of Finsler structure it is given by
Consequently, we have the solution
or
and
It is to be noted that the second Killing equation constrains the first one which is, in fact, the Killing equation of the Riemannian space, that is, it is responsible for breaking the symmetry (isometric) of the Riemannian space.
On the other hand, the Finsler space we are considering is, in fact, can be determined from a Riemannian manifold \(( M, g_{\mu \nu }(x))\) as we have
(cf. Eqs. (5) and (6) in the case \(\bar{F^2}\) is quadratic in \( y^\theta ~ \& ~y^\phi \)).
It is a semi-definite Finsler space. Therefore, we can take covariant derivative of the Riemannian space. The Bianchi identities are, in fact, coincident with those of the Riemannian space (being the covariant conservation of Einstein tensor). The present Finsler space is reducible to the Riemannian space and consequently the gravitational field equations can be obtained. Also we shall find the gravitational field equations alternatively following the Ref. [34]. They have also shown the covariantly conserved properties of the tensor \(G^\mu _\nu \) in respect of covariant derivative in Finsler spacetime with the Chern–Rund connection. Presently this conserved property of \(G^\mu _\nu \) which are, in fact, in the same forms but obtained from the Riemannian manifold follows by using the covariant derivative of that space (which are, in fact, the Bianchi identity). Also we point out the gravitational field equation (18) is restricted to the base manifold of the Finsler space, as in [47], and the fiber coordinates \(y^i\) are set to be the velocities of the cosmic components (velocities in the energy momentum tensor). Also, Li et al. [47] have shown that their gravitational field equation could be approximately derived from the Pfeifer et al. [48]. They [48] have constructed gravitational dynamic for Finsler spacetime in terms of an action integral on the unit tangent bundle. Also the gravitational field Eq. (18) is insensitive to the connection because \(G_\nu ^\mu \) are obtained from the Ricci scalar which is insensitive to the connections and depend only on the Finsler structure F.
Thus above Eqs. (20)–(22) are derived from the modified gravitational field equation (18) taking anisotropic energy momentum tensor (19) as well as these equations are derivable from the Einstein gravitational field equation in the Riemannian spacetime with the metric (6) in which the metric \(\bar{g}_{ij}\) is given by
That is
The terms involving \(\lambda \) in these equations are playing the physically meaning role doing the effect of the Finsler geometric consideration of the problem.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3
About this article
Cite this article
Rahaman, F., Paul, N., De, S.S. et al. The Finslerian compact star model. Eur. Phys. J. C 75, 564 (2015). https://doi.org/10.1140/epjc/s10052-015-3797-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-015-3797-7