Abstract
The ATLAS and CMS collaborations recently recorded possible excess in the di-boson production at the di-boson invariant mass at around 2 TeV. Such an excess may be produced if there exist additional \(Z^{\prime }\) and/or \(W^{\prime }\) at that scale. We survey the extra \(Z^{\prime }\)s and \(W^{\prime }\)s that may arise from semi-realistic heterotic-string vacua in the free fermionic formulation in the seven distinct cases: \(U(1)_{Z^{\prime }}\in SO(10)\); family universal \(U(1)_{Z^{\prime }}\notin SO(10)\); non-universal \(U(1)_{Z^{\prime }}\); hidden sector U(1) symmetries and kinetic mixing; left–right symmetric models; Pati–Salam models; leptophobic and custodial symmetries. Each case has a distinct signature associated with the extra symmetry breaking scale. In one of the cases we explore the discovery potential at the LHC using resonant leptoproduction. The existence of an extra vector boson with the reported properties will significantly constrain the space of allowed string vacua.
Similar content being viewed by others
1 Introduction
The Standard Model multiplet structure strongly favours its embedding in chiral 16 representations of SO(10). This can be most emphatically demonstrated by recalling that the Standard Model gauge charges are experimental observables. The Standard Model, including right-handed neutrinos, has three group factors, three generations, and six multiplets per family, and therefore heuristically the number of parameters required in the standard model is 54. Embedding the Standard Model states in SO(10) representations reduces this number to one, which is the number of 16 spinorial SO(10) representations required to accommodate the standard model states.
Gravitational interactions are not accounted for in the Standard Model. A contemporary self-consistent framework that facilitates the exploration of the synthesis of the gravitational and gauge interactions is provided by string theories, which are conjectured to be effective limits of a more fundamental theory. Heterotic-string theory is the perturbative limit that allows for the embedding of the Standard Model states in chiral SO(10) representations as it gives rise the spinorial 16 representations in its perturbative spectrum. Three generation models with viable gauge group and Higgs states have been constructed using a variety of methods. Among those the free fermionic formulation [1–3] of the heterotic string [4] provided a particularly fertile ground. In these three generation models the SO(10) symmetry is broken at the string level to one of its maximal subgroups.
Recently, the ATLAS and CMS collaborations [5–7] reported an excess in fat jet production which is kinematically compatible with the decay of a heavy resonance into two vector bosons, generating a wide range of interest [8–33]. A possible interpretation of the observed excess is as an extra \(Z^{\prime }\) or \(W^{\prime }\) with a mass of the order of few TeV [5, 6, 8–33]. The existence of an extra \(Z'\) inspired from heterotic-string theory attracted considerable interest in the particle physics literature [34–45]. However, constructing string models that allow an \(Z'\) to remain unbroken down to low scales has proven to be very challenging. The reason being that the extra U(1) symmetries that are studied in the literature are either anomalous or have to be broken at the high scale to generate qualitatively realistic fermion mass spectrum. Furthermore, flavour changing neutral current (FCNC) constraints indicate that the extra \(Z^{\prime }\), below the DecaTeV scale, has to be family universal and imposes an additional strong constraint on the viable string vacuum. Extra vector bosons in the TeV region will exclude the majority of heterotic-string models constructed to date. Recently, a semi-realistic string derived model that allows for a light \(Z^{\prime }\) model was constructed in Ref. [46].
In this paper we survey the various types of extra \(Z^{\prime }\)s that may arise from heterotic-string models. Our laboratory to examine this question is provided by the three generation heterotic-string models in the free fermionic formulation. This class of string vacua is related to \(Z_2\times Z_2\) orbifold compactification [52–55], but the properties of the models pertaining to the gauge group structure are relevant to other constructions [47–51]. The various \(Z^{\prime }\) that arise in the models may be classified into several broad categories:
-
Family universal U(1)s that admit the SO(10) and \(E_6\) embedding of the standard model charges.
-
Extra \(W^{\prime }\) and \(Z^{\prime }\) arising in left–right symmetric heterotic-string models.
-
Family non-universal U(1)s.
-
Hidden sector U(1) symmetries and kinetic mixing.
-
Extra vector bosons from extensions of the colour group.
-
Leptophobic and custodial SU(2) symmetries.
We will comment on these possibilities and their viability below the 10 TeV scale. We show that the possibility of extra hidden sector U(1)s is not viable in these models. Furthermore, each of the remaining cases carries a unique signature associated with extra gauge symmetry breaking scale. For example, \(U(1)_{Z^{\prime }}\in SO(10)\) only requires additional right-handed neutrinos for anomaly cancellation, whereas \(U(1)_{Z^{\prime }}\notin SO(10)\) mandates the existence of additional matter. Family non-universal U(1)s are constrained to be above the DecaTeV scale, whereas non-Abelian extensions of the Standard Model gauge symmetries, as in the left–right symmetric models, give rise to additional vector bosons. Discovery of one or more additional vector bosons at the LHC will therefore pave the way to discriminate between the different possibilities and will strengthen the case for a multi-TeV lepton collider and a 100 TeV hadron collider. In Sect. 4 we explore the discovery potential at the LHC using resonant leptoproduction.
2 Additional U(1)s in heterotic-string models
In this section we elaborate on the type of extra gauge bosons that may arise from heterotic-string vacua. Our discussion is in the framework of the free fermionic formulation. Details of the construction and the models that we discuss are given in the references provided and will not be repeated here. In this paper we only mention the features that are relevant for the discussion of the light extra \(W^{\prime }\)s and \(Z^{\prime }\)s, which are obtained from the untwisted Neveu–Schwarz sector. The last category that we consider includes vector bosons from additional sectors.
In the free fermionic formulation of the heterotic-string all the degrees of freedom needed to cancel the conformal anomaly are represented in terms of world-sheet fermions propagating on the string world-sheet. In the light-cone gauge in four dimensions 20 right-moving and 44 left-moving world-sheet real fermions are required. These are typically denoted
where in the right-moving bosonic sector the \(\left\{ {\bar{y}}^{1, \ldots 6}, {\bar{\omega }}^{1, \ldots 6}\right\} \) are real and \(\left\{ {\bar{\psi }}^{1, \ldots ,5}, {\bar{\eta }}^{1,2,3},{\bar{\phi }}^{1,\ldots ,8}\right\} \) are complex. A complex world-sheet fermion produces a U(1) current in the Cartan subalgebra of the string models. The 16 complex right-moving world sheet fermions therefore generate a rank 16 gauge group. Additional Cartan generators in the four dimensional gauge group may be obtained by complexifying additional world-sheet fermions from the set \(\left\{ {\bar{y}}^{1, \ldots 6}, {\bar{\omega }}^{1, \ldots 6}\right\} \). The five world-sheet complex fermions \({\bar{\psi }}^{1,\ldots ,5}\) are the Cartan generators of the SO(10) gauge symmetry and \({\bar{\eta }}^{1,2,3}\) generate three U(1) symmetries in the observable sector, denoted by \(U(1)_{1,2,3}\). The three generation free fermionic models typically contain up to three additional U(1) symmetries from the set of real fermions \(\left\{ {\bar{y}}^{1, \ldots 6}, {\bar{\omega }}^{1, \ldots 6}\right\} \), denoted by \(U(1)_{4,5,6}\). The symmetries discussed up to now are all in the observable sector, whereas the eight complex world-sheet fermions \({\bar{\phi }}^{1,\ldots ,8}\) correspond to the Cartan generators of the hidden sector gauge group. The distinction between hidden and observable entails that the states that are identified as the Standard Model states may carry charges under the observable gauge symmetries but may not carry hidden charges.
Under parallel transport around the noncontractible loops of the world-sheet torus of the vacuum to vacuum amplitude, the world-sheet fermions pick up a phase. The allowed phase assignments are constrained by the requirement that the vacuum to vacuum amplitude is invariant under modular transformations. Models in the free fermionic formulation are obtained by specifying a set of boundary basis vectors and the associated one-loop GGSO phases [1–3], which both must satisfy a set of constraints derived by the requirement that the vacuum to vacuum amplitude is invariant under modular transformations. In this paper we will focus on the so-called NAHE-based models [56], which are typically produced by a set of eight (or nine) boundary condition basis vectors denoted by \(\{\mathbf{1}, S, b_1, b_2, b_3, \alpha , \beta , \gamma \}\), where the set \(\{\mathbf{1}, S, b_1, b_2, b_3\}\) is the so-called NAHE set [56]. The basis vectors of the NAHE set preserve the SO(10) symmetry. Basis vectors that extend the NAHE set may preserve the SO(10) symmetry in which case they are denoted \(b_{4, 5, \ldots }\), or they may break the SO(10) symmetry, in which case they are denoted \(\{\alpha , \beta , \gamma , \ldots \}\). At least one basis vector beyond the NAHE set must break the SO(10) symmetry.
Space-time vector bosons in the free fermionic models arise from the untwisted Neveu–Schwarz sector and possibly from additional sectors that are obtained from combinations of the basis vectors. The vector bosons from these additional sectors enhance the gauge symmetry which is obtained from the untwisted NS sector. The generators of the SO(10) symmetry and of any additional U(1) symmetries are obtained from the untwisted NS sector. The vector bosons arising in the additional sectors do not play a role in the case of extra gauge symmetries from SO(10) subgroups, or from extra NS U(1) symmetries. They arise in the case of custodial symmetries [57]. The projection of the space-time vector bosons arising from the untwisted NS sector depends only on the boundary condition basis vectors, and it does not depend on the GGSO phases [1–3]. The type of enhancement from the additional sectors does depend on the GGSO phases, but it will not play a role in our discussion here. The boundary condition basis vectors, and the GGSO phases, leading to the models that we discuss, are given in the references.
The three sectors \(b_{1,2,3}\) correspond to the three twisted sectors of the \(Z_2\times Z_2\) orbifold. The basis vector S is the space-time supersymmetry generator, and ensures the projection of the untwisted NS tachyon. At the level of the NAHE set each of the twisted sectors produces 16 multiplets in the 16 spinorial representation of SO(10). The additional basis vectors beyond the NAHE set reduce the number of generations to three generations and at the same time break the SO(10) symmetry to one of its maximal subgroups. Semi-realistic models were obtained with:
-
\(SU(5)\times U(1)\) (FSU5) [58];
whereas the \(SU(4)\times SU(2)\times U(1)\) (SU421) class of models has been shown not to produce phenomenologically realistic examples [68–70].
All of the three generation free fermionic models share a common structure due to the underlying SO(10) symmetry and the spectrum available to break the U(1) symmetry which is embedded in SO(10) and is orthogonal to the weak hypercharge. In all these models this extra U(1) symmetry is necessarily broken by a Higgs field with charges identical to those of the right-handed neutrino, i.e. the Standard Model singlet that resides in the 16 spinorial representation of SO(10). The reason is the absence of the adjoint and higher level representations in the massless spectrum of these string models. All the semi-realistic models contain three chiral 16 representations of SO(10) decomposed under the final SO(10) subgroup and electroweak Higgs doublet representations that arise from the vectorial 10 representation of SO(10).
One distinction between the models is the scale at which the SO(10) extra U(1) has to be broken. For instance in the case of the FSU5 models it must be broken at the MSSM GUT scale, to generate masses for the \(SU(5)\times U(1)\) vector bosons which mediate proton decay via dimension six operators. In the three other cases it could in principle remain unbroken below that scale, because these models do not contain vector bosons that may mediate proton decay via dimension six operators.
Another distinction between the models is with respect to the anomalous U(1) symmetry that arises in the string models [71]. In the case of the FSU5, SLM and PS models, the \(U(1)_{1,2,3}\) symmetries, as well as their linear combination,
are anomalous, whereas in the LRS and SU421 models they are anomaly free. In the models in which this U(1) symmetry is anomalous it is broken by the Dine–Seiberg–Witten anomaly cancellation mechanism [72, 73], whereas in models in which it is anomaly free it could in principle remain unbroken down to low scales. The basic characteristic of the FSU5, SLM and PS cases in this regard is that they emanate from the symmetry breaking pattern \(E_6\rightarrow SO(10)\times U(1)_\zeta \), induced by the GGSO projections. In this case \(U(1)_\zeta \) becomes anomalous because the \(10+1 \) components in the 27 representation of \(E_6\) are projected out, resulting in \(U(1)_\zeta \) becoming anomalous. The LRS [66, 67] and SU421 models [68–70] circumvent the \(E_6\rightarrow SO(10)\times U(1)_\zeta \) symmetry breaking pattern with the price that the \(U(1)_\zeta \) charges of the Standard Model states do not satisfy the \(E_6\) embedding. It turns out that the \(E_6\) embedding is necessary for unified gauge couplings to agree with the low energy values of \(\sin ^2\theta _W(M_Z)\) and \(\alpha _s(M_Z)\) [74, 75]. The construction of string models that admit the \(E_6\) charges of the Standard Model states, while maintaining \(U(1)_\zeta \) as an anomaly free symmetry, was discussed in Ref. [76]. The basic element of the proposed construction is to keep the massless chiral states in complete 27 representations of \(E_6\), while the \(E_6\) symmetry is broken at the string level and is not manifest in the string vacuum. In Ref. [46] a PS heterotic-string derived model with anomaly free \(U(1)_\zeta \) was obtained by using the classification methodology developed in Refs. [77–80], and exploiting the spinor–vector duality that was discovered in Refs. [81–83]. The key ingredient is that the model of Ref. [46] is self-dual under the exchange of the total number of spinorial \(16\oplus \overline{16}\) and vectorial 10 representations of SO(10). This is the same condition as if the \(SO(10)\times U(1)_\zeta \) symmetry is enhanced to \(E_6\). However, in the model of Ref. [46] this is not the case, i.e. the SO(10) symmetry is not enhanced to \(E_6\). This is possible in the free fermionic model if the different 16 and \(10+1\) states, which would make a complete 27 of \(E_6\), are obtained from different fixed points of the underlying \(Z_2\times Z_2\) orbifold [46].
In the free fermionic SLM, PS and LRS models the weak hypercharge is given byFootnote 1
where \(B-L\) is baryon minus lepton number and \(T_{3_R}\) is the diagonal generator of \(SU(2)_R\). The SO(10) orthogonal combination is given by
The VEV of the Higgs field with the quantum charges of the right-handed neutrino leaves unbroken the \(U(1)_{{\mathcal {Z}}^{\prime }}\) combination,
that may remain unbroken down to low scales only if \(U(1)_\zeta \) is anomaly free.
2.1 Observable non-universal U(1)s
In addition to the family universal U(1) symmetries in the observable \(E_8\) gauge group, the string models contain two additional U(1) symmetries that are combinations of \(U(1)_{1,2,3}\) and are orthogonal to \(U(1)_\zeta \). These are family non-universal and therefore must be heavier than roughly 30 TeV due to flavour changing neutral current (FCNC) constraints [84]. Additional observable \(U(1)_{4,5,6}\) symmetries may arise from complexification of real fermions as discussed above. One combination of those may be family universal while the other two are not. In Ref. [85] it was proposed that the family universal anomaly free combination of \(U(1)_{1,2,3,4,5,6}\) in the model of Refs. [61, 62] plays a role in adequately suppressing proton decay mediating operators, as well as allowing for suppression of left-handed neutrino masses via the seesaw mechanism. However, it was shown in Ref. [86] that the U(1) discussed in Ref. [85] must in fact be broken near the string scale. This is expected as this U(1) symmetry is a combination of \(U(1)_\zeta \), which is anomalous, with the family universal combination of \(U(1)_{4,5,6}\). In Ref. [87] it was shown that two of the anomaly free non-universal combinations may similarly, adequately suppress proton decay and generate small neutrinos via a seesaw mechanism. As discussed above they must be broken above the DecaTeV scale. The additional combinations of \(U(1)_{1,2,3,4,5,6}\), aside from \(U(1)_\zeta \), will not be considered further here.
2.2 Hidden sector U(1)s
In addition to the U(1) symmetries that arise in the observable sector, the string models may contain \(U(1)_h\) symmetries that arise from the hidden \(E_8\) gauge group. Such \(U(1)_h\) symmetries may mix with the weak hypercharge via kinetic mixing [88–91] provided that there exist light states in the spectrum that are charged under both \(U(1)_Y\) and under the hidden sector \(U(1)_h\) factor. Depending on the details of the spectrum, kinetic mixing may then arise from one-loop radiative corrections [88–91] and is proportional to \(\mathrm{Tr}Q_YQ_h\).
The existence of hidden \(U(1)_h\) symmetries in semi-realistic heterotic-string models is highly model dependent, but there are some generic properties that may be highlighted. The PS class of models typically do not contain U(1) factors in the hidden sector. The reason being that the PS models utilise only periodic/antiperiodic boundary conditions, and that the set of basis vectors that generate a PS model typically contain a single SO(10) breaking vector.
The FSU5 models utilise rational boundary conditions, which break SO(2n) symmetries into \(SU(n)\times U(1)\). Provided that the hidden sector gauge symmetry is not enhanced, the hidden sector may contain unbroken U(1) factors. In the FSU5 model of Ref. [58] the hidden sector gauge group is enhanced and this model does not have any hidden sector U(1) factors. In the FSU5 models that were classified in Ref. [92] all the hidden sector gauge group enhancements are projected out and therefore these FSU5 models do contain two hidden U(1) symmetries.
The SLM [59–62, 93, 94] and LRS [66, 67] models utilise two basis vectors that break the SO(10) symmetry. These models generically contain several hidden sector U(1) factors, irrespective of whether the hidden sector symmetry is enhanced or not.
We now turn to a discussion of the matter states appearing in the models and the feasibility of kinetic mixing. Before getting into specific SO(10) subgroups several broad observations can be made. All the models that we discuss have \(N=1\) space-time supersymmetry, but the general properties that we extract are also applicable in tachyon free non-supersymmetric vacua [95–97]. The first division of the matter sectors is into those that preserve \(N=4\), and those that preserve \(N=2\), space-time supersymmetry. In the discussion of kinetic mixing it is sufficient to focus on the \(N=2\) sectors. These sectors are obtained from combinations of the basis vectors \(b_{1,2,3}\) with the other basis vectors. The basis vectors \(b_{1,2,3}\) in the NAHE-based models produce spinorial SO(10) representations that are neutral under the hidden sector. The sectors \(b_i+2\gamma \) produce states that transform as vector representations of the hidden sector gauge group, and they are singlets of the SO(10) subgroup. States that transform in the 10 vector representation of SO(10) are neutral under the hidden sector gauge group. All the sectors discussed thus far therefore cannot give rise to kinetic mixing with the weak hypercharge because they are not charged with respect to both \(U(1)_Y\) and \(U(1)_h\).
States that can induce kinetic mixing in free fermionic models can therefore only arise from sectors that break the SO(10) symmetry. These sectors arise in combinations of the basis vectors \(b_{1,2,3}\) with the SO(10) basis vectors \(\alpha , \beta , \gamma \). Here we can further divide into sectors that break the SO(10) symmetry to the PS or FSU5 subgroups. We will focus here on the examples of the FSU5 and SLM models. In the case of the FSU5 models all SO(10) breaking sectors contain states that carry fractional electric charge. The states may transform as singlets or fiveplets of SU(5) and both types of states will carry fractional electric charge. These states must therefore be decoupled from the massless spectrum [98, 99], or confined [58, 92], at a high scale and cannot generate sizeable kinetic mixing.
The SLM models contain a richer variety of SO(10) breaking sectors, which can be divided according to the surviving SO(10) subgroup, which can be \(SU(5)\times U(1)\), \(SO(6)\times SO(4)\) or \(SU(3)\times SU(2)\times U(1)^2\) [98, 99]. The first two cases produce states with fractional electric charge, which must be either decoupled or confined [98, 99]. The last category of states produces states that carry standard charges under the Standard Model gauge group but carry non-standard SO(10) charges under \(U(1)_{Z^{\prime }}\). One type of states in these sectors are neutral under the weak hypercharge and therefore cannot generate kinetic mixing. The other type of states arising in these sectors are states that transform as 3, \({\bar{3}}\) and 2, \({\bar{2}}\) of the observable SU(3) and SU(2) groups, respectively, and carry the standard Standard Model charge under \(U(1)_Y\). These states interact via the strong and electroweak interactions, and therefore cannot remain light to the required scale to produce sizeable mixing [88–91]. We conclude that kinetic mixing of a hidden sector \(U(1)_h\) with \(U(1)_Y\) is not viable in free fermionic models.
For concreteness we can elaborate on this structure in some of the specific heterotic-string standard-like models in the literature. For instance the model of Ref. [93], which is given by the NAHE set of basis vectors plus the basis vectors \(\{b_4, \beta , \gamma \}\) in Eq. (3.2) of [93]. In this model the observable and hidden sector gauge symmetries are given by
The entire spectrum of the model is given in Ref. [93]. The sectors \(b_i\), \(b_i+2\gamma \), \(b_4+2\gamma \), \(\mathbf{1}+b_1+b_2+b_3+b_4+2\gamma \) and the NS sector, where \(i=1,2,3\), produce states that are charged with respect to either \(U(1)_Y\) or \(U(1)_h\) but not with respect to both. The states in the sectors \(\mathbf{1}+b_j+b_k+2\gamma \), \(j\ne k=1,2,3\), are neutral with respect to both \(U(1)_Y\) and \(U(1)_h\). The sectors \(\mathbf{1} + b_4 +\beta +2\gamma \), \(\mathbf{1} + b_4 + \beta \), \(\mathbf{1} + b_1 +b_2 + b_4 \pm \gamma \), \(\mathbf{1} + b_1 +b_2 + b_3 +\beta +2\gamma \), \(\pm \gamma \), \(b_1+b_3\pm \gamma \), \(\mathbf{1} +b_4 + \pm \gamma \), \(b_3 +b_4 \pm \gamma \) and \(b_1 +b_2 +b_3 +b_4 \pm \gamma \) produce vector-like states that carry fractional \(\pm 1/2\) charge and must be decoupled or confined at a high scale [98, 99]. The sectors \(\mathbf{1} + b_3 + b_4 + \beta + \pm \gamma \) and \(\mathbf{1} + b_2 + b_4 + \beta + 2\gamma \) produce exotic states that are neutral under \(U(1)_Y\) and charged under \(U(1)_h\). Similar structure of the spectrum with respect to states that can potentially mix between \(U(1)_Y\) and \(U(1)_h\) arises in the models of Refs. [59–62, 94]. We conclude that kinetic mixing of \(U(1)_Y\) and \(U(1)_h\) in these free fermionic models is not viable.
3 Light U(1)s
In this section we consider the possibility that an extra U(1) symmetry is left-unbroken in the heterotic-string vacuum; the phenomenological constraints; and the distinctions between the different models. The four cases that we discuss are: (i) the \(U(1)_{Z^{\prime }}\) in Eq. (2.3); (ii) the \(U(1)_{{\mathcal {Z}}^{\prime }}\) in Eq. (2.3); (iii) the non-Abelian left–right symmetric extension \(SU(2)_R\times U(1)_C\); (iv) the PS models. For completeness we also mention two additional cases: (v) the \(SU(4)\times SU(2)\times U(1)_C\) models; (vi) the leptophobic \(Z^{\prime }\) and custodial SU(2) models.
The main phenomenological constraints are with respect to proton stability and the suppression of left-handed neutrino masses. Specifically, the simultaneous accommodation of both constraints is problematic. The reason is that while proton stability favours baryon number conservation, suppression of neutrino masses demands that lepton number is violated. In the free fermionic models baryon minus lepton number is gauged and therefore breaking lepton number implies that baryon number is broken as well, giving rise to dimension four proton decay mediating operators from non-renormalisable operators [100, 101],
where \(\phi ^n\) is a string of states that get a vacuum expectation value of the order of the string scale, whereas \({\mathcal {N}}\) and \({\bar{\mathcal {N}}}\) are the components of the heavy Higgs fields that break \(U(1)_{Z^{\prime }}\). The operators in Eq. (3.1) arise from the \(16^4\) operator of SO(10) and therefore arise in any of the string models discussed above. It is noted from (3.1) that the magnitude of the proton decay mediating operators is proportional to the scale of \(U(1)_{Z^{\prime }}\) breaking. This is a general feature of the SO(10)-based free fermionic models.
On the other hand the structure of the neutrino mass matrix is also quite generic in these models. In term of component fields, the terms in the superpotential that generate the neutrino mass matrix are (see e.g. [102]),
where \(L_i\), \(N_i\) and \(\phi _i\), with \(i,j,k=1,2,3\) are the lepton doublets; the right-handed neutrinos; and three SO(10) singlet fields, respectively; \({\bar{h}}\) is the electroweak Higgs doublet and \({\bar{\mathcal {N}}}\) is the component of the heavy Higgs field that breaks \(U(1)_{Z^{\prime }}\). All these states exist in the spectra of the string models, possibly as components of larger representation in, e.g., the FSU5 models. The neutrino seesaw mass matrix takes the generic form
where \(M_{_D}\) is the Dirac mass matrix arising from the first term in Eq. (3.2). Due to the underlying SO(10) symmetry the Dirac mass matrix is proportional to the up-quark matrix [102]. At the cubic level of the superpotential the symmetry dictates the equality of the top quark and tau neutrino Yukawa couplings. Hence, for the tau neutrino we have \(M_{_D}=k M_\mathrm{top}\), where k is a renormalisation factor due to RGE evolution. Taking the mass matrices to be diagonal, the mass eigenstates are primarily \(\nu _i\), \(N_i\) and \(\phi _i\) with negligible mixing and with the eigenvalues
Therefore, the left-handed neutrino masses are inversely proportional to the square of the \(U(1)_{Z^{\prime }}\) breaking scale and to the VEV of the SO(10) singlet field \(\phi \). This structure is generic in this class of models and the question is what is required in order to accommodate the left-handed neutrino masses in the different scenarios. Detailed studies of the neutrino masses in free fermionic models were performed in [103, 104]. Here we are only interested in the qualitative features. We can then consider several cases.
3.1 Case I: low \(B-L\) breaking scale
In this case the spectrum contains the MSSM states plus the right-handed neutrinos; a pair of Higgs doublets that break the electroweak symmetry and a pair of Higgs singlets that break the \(U(1)_{Z^{\prime }}\) symmetry [105]. The full spectrum is displayed in Table 1.
Taking \(m_t\sim 173\)GeV; \(k\sim 1/3\); \(\langle {\bar{\mathcal {N}}}\rangle \sim 3\) TeV we note that to accommodate a tau neutrino mass below 1eV we need \(\langle \phi \rangle \sim 1\)keV. While not impossible, it requires the introduction of a new scale, which may be ad hoc from the string model building perspective [103, 104].
3.2 Case II: high \(B-L\) breaking scale
In this case we assume that the VEV of \({\mathcal {N}}\) is high, or intermediate. Furthermore, we may assume that \(\langle \phi \rangle \sim 100\)GeV, i.e. that this VEV is associated with electroweak symmetry breaking. Then taking \(\langle {\bar{\mathcal {N}}}\rangle \sim 10^{17}\)GeV gives \(m_{\nu _\tau }\sim 10^{-20}\)GeV. Breaking \(U(1)_{Z^{\prime }}\) at the high scale therefore naturally produces light neutrino masses, with the scale of \(\langle \phi \rangle \) being associated with the electroweak breaking scale. In this case the combination \(U(1)_{{\mathcal {Z}}^{\prime }}\) in Eq. (2.4) remains unbroken. This is possible if and only if \(U(1)_\zeta \) is anomaly free. As discussed above this necessitates that the chiral states form complete 27 representations of \(E_6\). However, the normalisation of \(U(1)_{{\mathcal {Z}}^{\prime }}\) may differ from the standard \(E_6\) normalisation, similar to the discussion in relation to the normalisation of the weak hypercharge [106, 107]. The spectrum of the string inspired model that may keep \(U(1)_{{\mathcal {Z}}^{\prime }}\) unbroken down to the TeV scale is shown in Table 2. The effective dimension four operators induced from Eq. (3.1) are not invariant under \(U(1)_{{\mathcal {Z}}^{\prime }}\). Hence, the dimension four proton decay operators are suppressed as in the case with a low \(U(1)_{Z^{\prime }}\) of Sect. 3.1. The caveat is that the spectrum contains leptoquark representations that arise from the SO(10) vectorial 10 representation, and may mediate rapid proton decay [100, 101]. Additional discrete symmetries are required to guarantee adequate suppression of the dangerous operators. This issue arises generically in string inspired \({\mathcal {Z}}^{\prime }\) models with an underlying \(E_6\) symmetry [34–45], i.e. in all models in which \(U(1)_\zeta \) forms part of the low scale \(Z^{\prime }\). We note that this is not a problem in the model of Sect. 3.1 because there \(U(1)_\zeta \) does not enter into the combination of the low scale \(Z^{\prime }\). We note again that the root of the problem is the conflict between adequately suppressing proton decay mediating operators, which favours a low scale \(U(1)_{Z^{\prime }}\) and the constraint of left-handed neutrino masses, which works more naturally with \(U(1)_{Z^{\prime }}\) being broken at a high scale.
3.3 Case III: Low scale left–right symmetric models
In the LRS models with a low \(U(1)_{Z^{\prime }}\) breaking the Standard Model states are organised in representations of the low scale gauge symmetry,
In this case the \(U(1)_{Z^{\prime }}\) combination is identical to the combination given in Eq. (2.3). However, in this case additional \(W^{\prime }\) vector bosons arise. The spectrum of the model is shown in Table 3. The dimension four proton decay mediating operators arise from the terms
We note that as \(U(1)_{{\mathcal {Z}}^{\prime }}\) is broken at a high scale in this scenario both terms can be generated without the adequate suppression discussed in Refs. [86, 108]. However, as in Sect. 3.1 they are adequately suppressed due to the fact that \(U(1)_{Z^{\prime }}\) is broken at a low scale, i.e. \(U(1)_{B-L}\) is gauged down to low scales. The left–right symmetric models only require the existence of the right-handed neutrinos in the spectrum, but not the states from the vectorial 10 representation of SO(10). However, similar to the case in Sect. 3.1, a Yukawa coupling of the Dirac mass term for the tau neutrino is of the order of the top quark mass and we have to assume the existence of a scale of the order of 1KeV as in Sect. 3.1. This is the case in the LRS string derived model of Refs. [66, 67]. An alternative possibility that may be contemplated is that only the mass term of the top quark is generated at cubic order of the superpotential, whereas the coupling of the tau neutrino to the same Higgs bi-doublet is obtained from higher order nonrenormalisable terms. In this case the relation between the top quark and tau neutrino Dirac mass term can be avoided. The tau neutrino Yukawa coupling is equal to that of the tau lepton, where the two relevant mass terms are \(\lambda _t Q_L^tQ_R^th\) and \(\lambda _\tau L_L^tL_R^th\). Therefore up to running effects the tau neutrino Dirac mass term will be of the order of the tau lepton mass. Taking \(m_\tau \sim 1.776\)GeV and assuming a seesaw scale of the order of 10 TeV requires \(\langle \phi \rangle \sim 10\)MeV. An interesting observation is that the string derived left–right symmetric heterotic-string models allow for the nonrenormalisable terms
due to the \(U(1)_\zeta \) charges in these models, as displayed in Table 3. Assuming that the electrically neutral scalar component of \(L_R\) gets a VEV of the order of 3 TeV, we get a Majorana mass term for the left-handed neutrino of order \(\langle {\tilde{N}}\rangle ^2/M_S\), where \(M_S\) is a scale of the order of the string scale, \(M_S\sim 5\times 10^{17}\mathrm{GeV}\). The effective Majorana mass for the left-handed neutrinos is then of order \(10^{-1}\)eV. This possibility enables the breaking of \(SU(2)_R\) without the additional Higgs fields \({\mathcal {L}}_R\) and \({\bar{\mathcal {L}}}_R\), which is advantageous for gauge coupling unification [109, 110].
3.4 Case IV: low scale Pati–Salam models
In the PS models the low energy effective gauge symmetry below the string scale is the SO(10) subgroup \(SO(6)\times SO(4)\). The possibility of the Pati–Salam symmetry [111] at the TeV scale was discussed in Refs. [111–115]. Similarly to the case of \(U(1)_{Z^{\prime }}\) and the left–right symmetry models anomaly cancellation only requires the addition of three right-handed neutrinos to the Standard Model states. The vector bosons in this model do not generate Proton decay via dimension six operators. A low scale breaking of the PS symmetry can therefore be considered. The spectrum of the model is shown in Table 4.
A low scale breaking of the PS symmetry may be obtained via the VEV of the neutral scalar component in a \(({\bar{4}},1,2)\) representation, whereas a high scale breaking requires an additional pair of heavy Higgs fields, \({\bar{\mathcal {H}}}\oplus {\mathcal {H}}= ({\bar{4}}, 1,2)_{\mathcal {H}}~\oplus ~({ 4}, 1,2)_{\mathcal {H}}\), to break the symmetry along supersymmetric flat directions. The dimension four operators are induced from the quartic order terms \({\mathcal {Q}}_L{\mathcal {Q}}_L{\mathcal {Q}}_R{\mathcal {Q}}_R\) and \({\mathcal {Q}}_R{\mathcal {Q}}_R{\mathcal {Q}}_R{\mathcal {Q}}_R\). With a low breaking of \(SU(2)_R\) these operators are sufficiently suppressed. The PS model with a high scale breaking include the (6, 1, 1) representation to generate mass to the coloured states of the heavy Higgs states, via the couplings \({\bar{\mathcal {H}}}{\bar{\mathcal {H}}}D+{\mathcal {H}}{\mathcal {H}}D\). With a low scale breaking these states are not required because an additional pair of heavy Higgs states is not required as the breaking can be implemented along a non flat direction. In this model suppression of left-handed neutrino masses may be obtained by the generations of VEVs of the order of 1keV, similar to the discussion in Sect. 3.1, or may be generated from the quartic order coupling \({\mathcal {Q}}_R {\mathcal {Q}}_R {\mathcal {Q}}_R {\mathcal {Q}}_R\) as in Sect. 3.3. We note that the mass structure of the extra vector states in this PS scenario requires elaborate analysis, with the possibility that the charged \(W^{\prime }\)s are relatively light, whereas the neutral \(U(1)_{Z^{\prime }}\) is comparatively heavy, as is the case in the Standard Model. These considerations raise the prospect that there will be a need to probe the DecaTeV scale and above.
3.5 Case V: low scale \(SU(4)\times SU(2)\times U(1)_L\) models
For completeness we comment on the case with SO(10) broken to the \(SU(4)\times SU(2)\times U(1)_L\) model.Footnote 2 This model was considered in Ref. [116] as a field theory extension of the Standard Model. The field theory model considered in Ref. [116] utilises the Higgs field in the (15, 2, 1) representation of \(SU(4)\times SU(2)\times U(1)_L\), to avoid the relation between the Dirac mass terms of the top quark and the tau neutrino. The string models do not contain such representations and therefore the only available route to satisfy the neutrino mass constraints is to assume \(\langle \phi \rangle \sim 1\) keV. The \(SU(4)\times SU(2)\times U(1)\) choice for the SO(10) subgroup of the string model is attractive because it admits both the doublet–triplet splitting mechanism [117] and the doublet–doublet splitting mechanism [68–70]. However, as discussed above, while a field theory model consistent with the phenomenological constraints can be constructed [68–70], it was shown in Refs. [68–70] that such string models are not viable because it is not possible to form complete families. This demonstrates that the string constructions are more restrictive than the field theory constructions. This is anticipated, as the string framework consistently incorporates gravity into the construction. An alternative method to produce \(SU(4)\times SU(2)\times U(1)\) three generation vacua is by enhancement of the NS gauge group from additional sectors [57, 118, 119].
3.6 Case VI: leptophobic \(Z^{\prime }\) and custodial SU(2)s
Finally, we comment briefly on the possibility of generating leptophobic \(Z^{\prime }\) [118, 119] and custodial SU(2) symmetries [57] in the free fermionic heterotic-string models. As mentioned in Sect. 3.5 the gauge group arising from the NS sector may be enhanced by space-time vector bosons that are obtained from additional sectors in the additive group. Examples of such three generation string models were presented in Refs. [57, 66, 67, 118, 119]. In these models the three generations still arise from the sectors \(b_{1,2,3}\) and hence descend from the spinorial 16 representations of SO(10), but they transform in representations of the enhanced gauge symmetry. Leptophobic U(1)s are obtained when \(U(1)_{B-L}\) combines with the a universal combination of the horizontal flavour symmetries to cancel out the lepton number and produce a gauged \(U(1)_B\) [118, 119]. We note that in the custodial SU(2) model only the lepton transforms as doublets of \(SU(2)_C\) [57]. Hence, the model will have distinct signature compared to the LRS models of Sect. 3.3. Namely, the additional \(W^{\prime }\) vector bosons couple to leptons but not to the hadrons, whereas a leptophobic \(Z^{\prime }\) [118, 119] couples to hadrons but not to the leptons.
4 Prospects at the LHC
In this section we illustrate LHC prospects for a hypothetical phenomenological scenario of a low scale heterotic-string derived \(Z^{\prime }\), based on the high \(B-L\) breaking scale model of Sect. 3.2. In particular, we show the LHC 8 TeV Drell–Yan (DY) invariant mass distribution at the next-to-next-to leading order (NNLO) in the QCD strong coupling constant (\({\mathcal {O}}(\alpha _s^2)\)) [120], for the production of a \(Z'\) with mass \(M_{Z'} = 3\) TeV.
Recently, the ATLAS [121] and CMS [122] collaborations have published measurements of the DY differential cross section \(\text {d}\sigma /\text {d}M\) in bins of dilepton invariant mass M at center-of-mass energies \(\sqrt{S}\) of 7 and 8 TeV. In particular, \(\text {d}\sigma /\text {d}M\) has been measured as a function of the invariant mass of dielectron and dimuon pairs, up to 2 TeV. These measurements are very precise in the mass region around the \(Z_0\) peak, and no significant deviations from the SM prediction have been observed in the mass range explored. However, data at large invariant mass are still affected by large uncertainties due to systematical, statistical and luminosity errors.
The uncertainty associated to scale variation of the NNLO QCD theory prediction amounts to a few percent, while that associated to the parton distribution functions (PDFs) luminosity is larger than 15 %, especially in the large invariant mass region. In this kinematic region PDFs are probed at large x, where they are in general not well constrained. This has a significant impact on the parton luminosity uncertainties as they are the major source of uncertainty and represent a limiting factor to obtain precise predictions for the production of high-mass dilepton resonances.
LHC run-II will allow us to measure this and other differential observables with higher precision in the high-mass region, and thus will confirm or rule out the existence of extra \(Z'\)s in the mass range of a few TeV.
4.1 Details of the calculation
In this section we briefly describe the details of the calculation and the choice of the parameter space. Electroweak corrections [123–128] are not included here, a more thorough analysis exploiting other differential observables [129, 130] is left for future studies.
The theory is calculated by using an amended version of CandiaDY [131, 132], a program that calculates the DY invariant mass distribution up to NNLO in QCD for a large variety of \(Z'\) string derived models. The full spin correlations as well as the \(\gamma ^*/Z/Z'\) interference effects are included in this calculation. The charge assignment is that of the high \(B-L\) breaking scale model described in Sect. 3.2 and is given in Table 2. Furthermore, we have chosen \(\tan \beta =10\), the \(Z'\) coupling constant \(g_z\) equal to the hypercharge \(g_Y\) and \(M_{Z'}=\) 3 TeV.
The colour-averaged inclusive differential cross section is given by
where (\(V=Z, Z^{\prime }\)), and all the hadronic initial state information is contained in the hadronic structure function which is defined as
The contribution \(W_{V}\) takes into account all the initial state emissions of real gluons and all the virtual corrections, while \(\sigma _{V}\) is the point-like cross section. The parton luminosity \({\mathcal {L}}_{i,j}\) includes combinations of PDFs relative to the partonic structure of the initial state, while the hard scattering contributions, denoted by \(\Delta _{i,j}(x,M^2,\mu _F^2)\), can be perturbatively expanded in terms of the strong coupling constant \(\alpha _s(\mu _R^2)\),
\(\mu _F\) and \(\mu _R\) are the factorisation and renormalisation scales respectively, while the invariant mass of the dilepton pair is denoted by M.
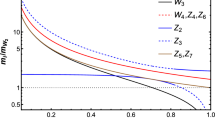
Left: LHC 8 TeV DY invariant mass distribution at NNLO for a case (ii) high \(B-L\) breaking scale \(Z'\). \(M_{Z^{{\prime }}}=3\) TeV, \(\tan \beta =10\), and \(Z'\) coupling \(g_z=g_Y\). Hatched bands represent PDFs + scale uncertainties added in quadrature. Right: same as on the left, but normalised to the SM
We strictly follow the notation introduced in Ref. [131] and here we briefly recall the main definitions. The fermion–fermion–\(Z^{{\prime }}\) interaction is given by
where \(f=e_{R}^{j},l_{L}^{j},u_{R}^{j},d_{R}^{j},q_{L}^{j}\) and \(q_L^{j}=\left( u_{L}^{j},d_{L}^{j}\right) \,\,,l_L^{j}=\left( \nu _{L}^{j},e_{L}^{j}\right) \). The coefficients \(z_{u},z_{d}\) are the charges of the right-handed up and down quarks, respectively, while the \(z_q\) coefficients are the charges of the left-handed quarks.
The masses of the neutral gauge bosons are parametrised in terms of the charges and vev’s of the higgs sector as
where \(\varepsilon \) is defined as a perturbative parameter, and where \(g=e/\sin \theta _W\) \(g_Y= e/\cos \theta _W\). The interaction Lagrangian for the quarks and the leptons is written as
where the left-handed (L) and right-handed (R) couplings for the quarks are
Similar expressions can be written for the leptons.
The main phenomenological results for the high \(B-L\) breaking scale model are illustrated in Fig. 1. The left figure shows the \(Z'\) invariant mass distribution (blue) compared to the SM (black) while, in the right figure, the same prediction is normalised to that of the SM in the 1–2 TeV mass range. Bands with different hatching represent the sum in quadrature of the uncertainty relative to the CT14NNLO PDFs [133] rescaled to the 68 % C.L., plus the uncertainty associated to independent variations of the \(\mu _F\) and \(\mu _R\) scales. Different choices for the PDFs, obtained from recent analyses [134–136] including LHC run-I measurements, give similar results. The heterotic-string prediction is almost indistinguishable from the SM in the 1 TeV mass region, and deviations start to be more evident around 2 TeV where the central value starts to rise. In the high-mass region far from the resonance, the SM central value is larger than the heterotic-string prediction, but there is a substantial overlap between the two uncertainty bands. The decay width of the \(Z^{\prime }\) predicted by this model is \(\Gamma _{Z^{\prime }} = 8.76\) GeV that is more than three times larger than that of the SM \(Z_0\).
5 Conclusions
In this paper we surveyed the possibility of low scale \(Z^{\prime }\)s and \(W^{\prime }\)s in three generation heterotic-string vacua. The semi-realistic free fermionic models produce the Standard Model spectrum and the necessary Higgs states for viable symmetry breaking and fermion mass generation. The models possess the SO(10) embedding of the Standard Model state and the SO(10) normalisation of the weak hypercharge. Hence, they can reproduce viable values of \(\sin ^2\theta _W(M_Z)\) and \(\alpha _s(M_Z)\). These are the first order criteria that a viable string vacuum should obey. The next major constraints on the string models are proton stability and suppression of left-handed neutrino masses. These two constraints are in tension because on the one hand proton stability prefers a low scale \(U(1)_{Z^{\prime }}\) breaking, whereas suppression of neutrino masses works more naturally with a high scale \(U(1)_{Z^{\prime }}\) breaking. As we discussed in Sect. 3.1 low scale \(U(1)_{Z^{\prime }}\) breaking requires the introduction of the ad hoc VEV \(\langle \phi \rangle \sim 1\)keV. The alternative \({\mathcal {Z}}^{\prime }\) discussed in Sect. 3.2 uses a high scale \(U(1)_{Z^{\prime }}\) breaking but anomaly cancellation necessitates the augmentation of the spectrum into complete 27 multiplets, potentially generating new proton decay operators. We further remark that while field theory models allow much more model building freedom, the straitjacket imposed by synthesising the Standard Model with gravity in the framework of string theory is by far more restrictive.
Each of the cases discussed in Sect. 3 has a distinct signature. Case I in Sect. 3.1 has an additional \(Z^{\prime }\) but no additional states charged under the Standard Model, with the only additional particles being the three right-handed neutrinos. Case II of Sect. 3.2 requires the existence of additional colour triplets and electroweak doublets in the vicinity of the \({\mathcal {Z}}^{\prime }\) breaking scale. Case III of the left–right symmetric models of Sect. 3.3 contains \(W^{\prime }\)s in addition to \(Z^{\prime }\). Similarly, case IV of Sect. 3.4 gives rise to additional vector bosons from the SU(4), and \(SU(2)_R\) group factors. Case V in Sect. 3.5 produces the SU(4) vector bosons but not the \(SU(2)_R\). Finally, in the models of case IV with a leptophobic \(Z^{\prime }\) or custodial SU(2) the additional vector bosons couple to either the quarks or the leptons but not to both.
For case II of Sect. 3.2 we studied the NNLO Drell–Yan invariant mass distribution at the LHC 8 TeV for a \(Z'\) with mass \(M_{Z'} = 3\) TeV, and estimated the main sources of uncertainty in the QCD theory prediction. The uncertainty associated to the partonic content of the proton is the dominant one and is a limiting factor for precision at the present time.
Observations of one or more additional vector bosons at the LHC will choose the right model or eliminate all of the above, and in fact, the majority of semi-realistic string models constructed to date. Furthermore, the observation of additional vector bosons at the LHC will restrict the exploration of string vacua, and it will elevate the utility of high-energy dilepton pair production at hadron colliders.
Notes
\(U(1)_C=3/2 U(1)_{B-L}\) and \(U(1)_L= 2 U(1)_{T_{3_R}}\) are used in free fermionic models and will also be used below.
we note that \(U(1)_L= 2 U(1)_{T_{3_R}}\), where \(T_{3_R}\) is the diagonal generator of \(SU(2)_R\).
References
H. Kawai, D.C. Lewellen, S.H.-H. Tye, Nucl. Phys. B 288, 1 (1987)
I. Antoniadis, C. Bachas, C. Kounnas, Nucl. Phys. B 289, 87 (1987)
I. Antoniadis, C. Bachas, Nucl. Phys. B 298, 586 (1987)
D.J. Gross, J.A. Harvey, E.J. Martinec, R. Rohm, Nucl. Phys. B 267, 75 (1986)
G. Aad et al. [ATLAS Collaboration], arXiv:1506.00962
V. Khachatryan et al., [CMS Collaboration]. JHEP 1408, 173 (2014). arXiv:1405.1994
V. Khachatryan et al., [CMS Collaboration]. JHEP 1408, 174 (2014). arXiv:1405.3447
B.A. Dobrescu, Z . Liu, arXiv:1506.06736
B.A. Dobrescu, Z . Liu, arXiv:1507.01923
K. Cheung, W.Y. Keung, P.Y. Tseng, T.C. Yuan, arXiv:1506.06064
J.A. Aguilar-Saavedra, arXiv:1506.06739
A. Thamm, R. Torre, A. Wulzer, arXiv:1506.08688
J. Brehmer, J. Hewett, J. Kopp, T. Rizzo, J. Tattersall, arXiv:1507.00013
G. Cacciapaglia, M.T. Frandsen, arXiv:1507.00900
Q.H. Cao, B. Yan, D.M. Zhang, arXiv:1507.00268
T. Abe, R. Nagai, S. Okawa, M. Tanabashi, arXiv:1507.01185
B.C. Allanach, B. Gripaios, D. Sutherland, arXiv:1507.01638
A. Carmona, A. Delgado, M. Quiros, J. Santiago, arXiv:1507.01914
T. Abe, T. Kitahara, M. M. Nojiri, arXiv:1507.01681
G. Cacciapaglia, A. Deandrea, M. Hashimoto, arXiv:1507.03098
V. Sanz, arXiv:1507.03553
C.H. Chen, T. Nomura, arXiv:1507.04431
W. Chao, arXiv:1507.05310
L.A. Anchordoqui et al., arXiv:1507.05299
L. Bian, D. Liu, J. Shu, arXiv:1507.06018
J. Hisano, N. Nagata, Y. Omura, arXiv:1506.03931
Y. Omura, K. Tobe, K. Tsumura, arXiv:1507.05028
Y. Gao, T. Ghosh, K. Sinha, J. H. Yu, arXiv:1506.07511
A. Alves, A. Berlin, S. Profumo, arXiv:1506.06767
S. Patra, F.S. Queiroz, W. Rodejohann, arXiv:1506.03456
H.S. Fukano, M. Kurachi, S. Matsuzaki, K. Terashi, K. Yamawaki, arXiv:1506.03751
H.S. Fukano, S. Matsuzaki, K. Yamawaki, arXiv:1507.03428
C.W. Chiang, H. Fukuda, K. Harigaya, M. Ibe, T.T. Yanagida, arXiv:1507.02483
G. Costa, J.R. Ellis, G.L. Fogli, D.V. Nanopoulos, F. Zwirner, Nucl. Phys. B 297, 244 (1988)
F. Zwirner, Int. J. Mod. Phys. A3, 49 (1988)
J.L. Hewett, T.G. Rizzo, Phys. Rep. 183, 193 (1989)
Y.Y. Komachenko, M.Y. Khlopov, Sov. J. Nucl. Phys. 51, 692 (1990)
Y.Y. Komachenko, M.Y. Khlopov, Yad. Fiz. 51, 1081 (1990)
G. Cleaver, M. Cvetic, J.R. Espinosa, L.L. Everett, P. Langacker, Phys. Rev. D 57, 2701 (1998)
A. Leike, Phys. Rep. 317, 143 (1999)
S.F. King, S. Moretti, R. Nevzorov, Phys. Rev. D 73, 035009 (2006)
P. Langacker, Rev. Mod. Phys. 81, 1199 (2009)
P. Athron, S.F. King, D.J. Miller, S. Moretti, R. Nevzorov, Phys. Rev. D 80, 035009 (2009)
M. Ambroso, B.A. Ovrut, Int. J. Mod. Phys. A 26, 1569 (2011)
A. Belyaev, S.F. King, P. Svantesson, arXiv:1303.0770 [hep-ph]
A.E. Faraggi, J. Rizos, Nucl. Phys. B 895, 233 (2015)
L.E. Ibanez, J.E. Kim, H.P. Nilles, F. Quevedo, Phys. Lett. B 191, 282 (1987)
D. Bailin, A. Love, S. Thomas, Phys. Lett. B 194, 385 (1987)
T. Kobayashi, S. Raby, R.J. Zhang, Nucl. Phys. B 704, 3 (2005)
O. Lebedev et al., Phys. Lett. B 645, 88 (2007)
M. Blaszczyk et al., Phys. Lett. B 683, 340 (2010)
A.E. Faraggi, Phys. Lett. B 326, 62 (1994)
A.E. Faraggi, Phys. Lett. B 544, 207 (2002)
E. Kiritsis, C. Kounnas, Nucl. Phys. B 503, 117 (1997)
A.E. Faraggi, S. Forste, C. Timirgaziu, JHEP 0608, 057 (2006)
A.E. Faraggi, D.V. Nanopoulos, Phys. Rev. D 48, 3288 (1993)
A.E. Faraggi, Phys. Lett. B 399, 223 (1994)
I. Antoniadis, J. Ellis, J. Hagelin, D.V. Nanopoulos, Phys. Lett. B 231, 65 (1989)
A.E. Faraggi, D.V. Nanopoulos, K. Yuan, Nucl. Phys. B 335, 347 (1990)
G.B. Cleaver, A.E. Faraggi, D.V. Nanopoulos, Phys. Lett. B 455, 135 (1999)
A.E. Faraggi, Phys. Lett. B 278, 131 (1992)
A.E. Faraggi, Nucl. Phys. B 387, 239 (1992)
I. Antoniadis, G.K. Leontaris, J. Rizos, Phys. Lett. B 245, 161 (1990)
G.K. Leontaris, J. Rizos, Nucl. Phys. B 554, 3 (1999)
K. Christodoulides, A.E. Faraggi, J. Rizos, Phys. Lett. B 702, 81 (2011)
G.B. Cleaver, A.E. Faraggi, C. Savage, Phys. Rev. D 63, 066001 (2001)
G.B. Cleaver, D.J. Clements, A.E. Faraggi, Phys. Rev. D 65, 106003 (2002)
G.B. Cleaver, A.E. Faraggi, S.E.M. Nooij, Nucl. Phys. B 672, 64 (2003)
A.E. Faraggi, H. Sonmez, Phys. Rev. D 91, 066006 (2015)
H. Sonmez, arXiv:1503.01193
G.B. Cleaver, A.E. Faraggi, Int. J. Mod. Phys. A 14, 2335 (1999)
M. Dine, N. Seiberg, E. Witten, Nucl. Phys. B 289, 589 (1987)
J.J. Atick, L.J. Dixon, A. Sen, Phys. Rev. D 292, 109 (1987)
A.E. Faraggi, V.M. Mehta, Phys. Rev. D 84, 086006 (2011)
A.E. Faraggi, V.M. Mehta, Phys. Rev. D 88, 025006 (2013)
P. Athanasopoulos, A.E. Faraggi, V. Mehta, Phys. Rev. D 89, 105023 (2014)
A.E. Faraggi, C. Kounnas, S.E.M. Nooij, J. Rizos, Nucl. Phys. B 695, 41 (2004)
A.E. Faraggi, C. Kounnas, J. Rizos, Phys. Lett. B 648, 84 (2007)
B. Assel et al., Phys. Lett. B 683, 306 (2010)
B. Assel et al., Nucl. Phys. B 844, 365 (2011)
A.E. Faraggi, C. Kounnas, J. Rizos, Nucl. Phys. B 774, 208 (2007)
C. Angelantonj, A.E. Faraggi, M. Tsulaia, JHEP 1007, 004 (2010)
A.E. Faraggi, I. Florakis, T. Mohaupt, M. Tsulaia, Nucl. Phys. B 848, 332 (2011)
G.B. Cleaver, A.E. Faraggi, D.V. Nanopoulos, T. ter Veldhuis, Mod. Phys. Lett. A 16, 3565 (2001)
J. Pati, Phys. Lett. B 388, 532 (1996)
A.E. Faraggi, Phys. Lett. B 499, 147 (2001)
A.E. Faraggi, M. Thormeier, Nucl. Phys. B 624, 163 (2002)
B. Holdom, Phys. Lett. B 166, 196 (1986)
K.R. Dienes, C.F. Kolda, J. March-Russell, Nucl. Phys. B 492, 104 (1997)
S.A. Abel, M.D. Goodsell, J. Jaeckel, V.V. Khoze, A. Ringwald, JHEP 0807, 124 (2008)
M. Goodsell, S. Ramos-Sanchez, A. Ringwald, JHEP 1201, 021 (2012)
A.E. Faraggi, J. Rizos, H. Sonmez, Nucl. Phys. B 886, 202 (2014)
A.E. Faraggi, E. Manno, C. Timirgaziu, Eur. Phys. J. C 50, 701 (2007)
G.B. Cleaver, A.E. Faraggi, E. Manno, C. Timirgaziu, Phys. Rev. D 78, 046009 (2008)
M. Blaszczyk, S. Groot Nibbelink, O. Loukas, S. Ramos-Sanchez, JHEP 1410, 119 (2014)
J.M Ashfaque, P. Athanasopoulos, A.E. Faraggi, H. Sonmez, arXiv:1506.03114
M. Blaszczyk, S.G. Nibbelink, O. Loukas, F. Ruehle, arXiv:1507.06147
A.E. Faraggi, Phys. Rev. D 46, 3204 (1992)
C. Coriano, S. Chang, A.E. Faraggi, Nucl. Phys. B 477, 65 (1996)
A.E. Faraggi, Nucl. Phys. B 403, 101 (1993)
A.E. Faraggi, Nucl. Phys. B 428, 111 (1994)
A.E. Faraggi, Phys. Lett. B 245, 435 (1990)
A.E. Faraggi, E. Halyo, Phys. Lett. B 307, 311 (1993)
C. Coriano, A.E. Faraggi, Phys. Lett. B 581, 99 (2004)
A.E. Faraggi, D.V. Nanopoulos, Mod. Phys. Lett. A 6, 61 (1991)
L. Ibanez, Phys. Lett. B 318, 73 (1993)
K.R. Dienes, A.E. Faraggi, J. March-Russell, Nucl. Phys. B 267, 44 (1996)
C. Coriano, A.E. Faraggi, M. Guzzi, Eur. Phys. J. C 53, 421 (2008)
A.E. Faraggi, Phys. Lett. B 302, 202 (1993)
K.R. Dienes, A.E. Faraggi, Nucl. Phys. B 457, 409 (1995)
J. Pati, A. Salam, Phys. Rev. D 10, 275 (1974)
A. Kuznetsov, M. Mikheev, Phys. Lett. B 329, 295 (1994)
G. Valencia, S. Willenbrock, Phys. Rev. D 50, 6843 (1994)
R.R. Volkas, Phys. Rev. D 53, 2681 (1996)
R. Foot, Phys. Lett. B 420, 333 (1998)
P. Fileviez Perez, M.B. Wise, Phys. Rev. D 88, 057703 (2013)
A.E. Faraggi, Phys. Lett. B 520, 337 (2001)
A.E. Faraggi, M. Masip, Phys. Lett. B 388, 524 (1996)
A.E. Faraggi, V. Mehta, Phys. Lett. B 703, 025006 (2011)
R. Hamberg, W.L. Van Neerven, T. Matsuura, Nucl. Phys. B 359, 343 (1991)
The ATLAS Collaboration, Phys. Lett. B 725, 223 (2013). arXiv:1305.4192
The CMS Collaboration, Eur. Phys. J. C 75, 147 (2015). arXiv:1412.1115
G. Balossini, C.M. Carloni Calame, G. Montagna, M. Moretti, O. Nicrosini, F. Piccinini, M. Treccani, A. Vicini Proceedings, Workshop on Monte Carlo’s, Physics and Simulations at the LHC. Part II, vol. 78 (2006)
G. Balossini, G. Montagna, C.M. Carloni Calame, M. Moretti, M. Treccani, O. Nicrosini, F. Piccinini, A. Vicini, Acta Phys. Polon. B 39 2008. arXiv:0805.1129
U. Baur, O. Brein, W. Hollik, C. Schappacher, D. Wackeroth, Phys. Rev. D 65, 033007 (2002). arXiv:hep-ph/0108274
V.A. Zykunov, Phys. Rev. D 75, 073019 (2007). arXiv:hep-ph/0509315
C.M. Carloni Calame, G. Montagna, O. Nicrosini, A. Vicini, JHEP 10, 109 (2007). arXiv:0710.1722
A. Arbuzov, D. Bardin, S. Bondarenko, P. Christova, L. Kalinovskaya, G. Nanava, R. Sadykov, Eur. Phys. J. C 54, 451 (2008)
R. Gavin, Y. Li, F. Petriello, S. Quackenbush, Comput. Phys. Commun. 184, 208 (2013). arXiv:1201.5896
Y. Li, F. Petriello, Phys. Rev. D 86, 094034 (2012). arXiv:1208.5967
C. Corianò, A.E. Faraggi, M. Guzzi, Phys. Rev. D 78, 015012 (2008)
A. Cafarella, C. Corianò, M. Guzzi, JHEP 08, 030 (2007). arXiv:hep-ph/0702244
S. Dulat, T.-J. Hou, J. Gao, M. Guzzi, J. Huston, P. Nadolsky, J. Pumplin, C. Schmidt, D. Stump, C.-P. Yuan, arXiv:1506.07443
The NNPDF Collaboration, JHEP 1504, 040 (2015). arXiv:1410.8849
L.A. Harland-Lang, A.D. Martin, P. Motylinski, R.S. Thorne, Eur. Phys. J. C 75, 204 (2015). arXiv:1412.3989
S. Alekhin, J. Blüumlein, S.-O. Moch, Phys. Rev. D 89, 054028 (2014). arXiv:1310.3059
Acknowledgments
AEF thanks the theoretical physics groups at CERN and Oxford University for hospitality. This work was supported in part by the STFC (ST/L000431/1) and by the Lancaster–Manchester–Sheffield Consortium for Fundamental Physics under STFC Grant ST/L000520/1.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted use, distribution, and reproduction in any medium, provided you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
Funded by SCOAP3.
About this article
Cite this article
Faraggi, A.E., Guzzi, M. Extra \(Z^{\prime }\)s and \(W^{\prime }\)s in heterotic-string derived models. Eur. Phys. J. C 75, 537 (2015). https://doi.org/10.1140/epjc/s10052-015-3763-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjc/s10052-015-3763-4