Abstract
Motivated by recent experimental observations [Rowley et al. in Phys Rev 96:020407, 2017] on hexagonal ferrites, we revisit the phase diagrams of diluted magnets close to the lattice percolation threshold. We perform large-scale Monte Carlo simulations of XY and Heisenberg models on both simple cubic lattices and lattices representing the crystal structure of the hexagonal ferrites. Close to the percolation threshold \(p_\mathrm{c}\), we find that the magnetic ordering temperature \(T_\mathrm{c}\) depends on the dilution p via the power law \(T_\mathrm{c} \sim |p-p_\mathrm{c}|^\phi \) with exponent \(\phi =1.09\), in agreement with classical percolation theory. However, this asymptotic critical region is very narrow, \(|p-p_\mathrm{c}| \lesssim 0.04\). Outside of it, the shape of the phase boundary is well described, over a wide range of dilutions, by a nonuniversal power law with an exponent somewhat below unity. Nonetheless, the percolation scenario does not reproduce the experimentally observed relation \(T_\mathrm{c} \sim (x_\mathrm{c} -x)^{2/3}\) in PbFe\(_{12-x}\)Ga\(_x\)O\(_{19}\). We discuss the generality of our findings as well as implications for the physics of diluted hexagonal ferrites.
Graphic abstract












Similar content being viewed by others
Data Availability Statement
This manuscript has no associated data or the data will not be deposited. [Authors’ comment: The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request.]
Notes
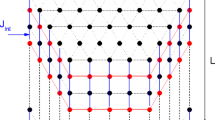
The lattice in question is the lattice of exchange interactions between the Fe ions.
References
G. Grinstein, A. Luther, Phys. Rev. B 13, 1329 (1976)
D.S. Fisher, Phys. Rev. Lett. 69, 534 (1992)
D.S. Fisher, Phys. Rev. B 51, 6411 (1995)
R.B. Griffiths, Phys. Rev. Lett. 23, 17 (1969)
M. Thill, D.A. Huse, Phys. A 214, 321 (1995)
A.P. Young, H. Rieger, Phys. Rev. B 53, 8486 (1996)
T. Vojta, Phys. Rev. Lett. 90, 107202 (2003)
R. Sknepnek, T. Vojta, Phys. Rev. B 69, 174410 (2004)
G. Schehr, H. Rieger, Phys. Rev. Lett. 96, 227201 (2006)
J.A. Hoyos, T. Vojta, Phys. Rev. Lett. 100, 240601 (2008)
T. Vojta, J. Phys. A 39, R143 (2006)
T. Vojta, J. Low Temp. Phys. 161, 299 (2010)
T. Vojta, Ann. Rev. Condens. Mat. Phys. 10, 233 (2019)
D. Stauffer, A. Aharony, Introduction to Percolation Theory (CRC Press, Boca Raton, 1991)
S.E. Rowley, T. Vojta, A.T. Jones, W. Guo, J. Oliveira, F.D. Morrison, N. Lindfield, E. Baggio Saitovitch, B.E. Watts, J.F. Scott, Phys. Rev. B 96, 020407 (2017)
G. Albanese, F. Leccabue, B.E. Watts, S. Díaz-Castañón, J. Mat. Sci. 37, 3759 (2002)
A. Coniglio, Phys. Rev. Lett. 46, 250 (1981)
T. Vojta, J. A. Hoyos, in Recent Progress in Many-Body Theories, ed. by J. Boronat, G. Astrakharchik, F. Mazzanti (World Scientific, Singapore, 2008) p. 235
C. Wu, Z. Yu, K. Sun, J. Nie, R. Guo, H. Liu, X. Jiang, Z. Lan, Sci. Rep. 6, 36200 (2016)
E. Shender, B. Shklovskii, Phys. Lett. A 55, 77 (1975)
B. Kozlov, M. Laguës, Phys. A: Statist. Mech. Appl. 389, 5339 (2010)
J. Wang, Z. Zhou, W. Zhang, T.M. Garoni, Y. Deng, Phys. Rev. E 87, 052107 (2013a)
A.B. Harris, T.C. Lubensky, J. Phys. A 17, L609 (1984)
A.B. Harris, A. Aharony, Phys. Rev. B 40, 7230 (1989)
U. Wolff, Phys. Rev. Lett. 62, 361 (1989)
N. Metropolis, S. Ulam, J. Am. Statist. Assoc. 44, 335 (1949)
H.G. Ballesteros, L.A. Fernández, V. Martín-Mayor, A. Muñoz Sudupe, G. Parisi, J.J. Ruiz-Lorenzo, Phys. Rev. B 58, 2740 (1998)
T. Vojta, R. Sknepnek, Phys. Rev. B 74, 094415 (2006)
Q. Zhu, X. Wan, R. Narayanan, J.A. Hoyos, T. Vojta, Phys. Rev. B 91, 224201 (2015)
K. Binder, Zeitschr. für Phys. B 43, 119 (1981)
W. Selke, L.N. Shchur, J. Phys. A 38, L739 (2005)
A.P. Gottlob, M. Hasenbusch, Phys. A Statist. Mech. Appl. 201, 593 (1993)
R.G. Brown, M. Ciftan, Phys. Rev. B 74, 224413 (2006)
S.E. Rowley, Y.-S. Chai, S.-P. Shen, Y. Sun, A.T. Jones, B.E. Watts, J.F. Scott, Sci. Rep. 6, 25724 (2016)
Acknowledgements
We acknowledge support from the NSF under Grant nos. DMR-1506152, DMR-1828489, and OAC-1919789. The simulations were performed on the Pegasus and Foundry clusters at Missouri S&T. We also thank Martin Puschmann for helpful discussions.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Khairnar, G., Lerch, C. & Vojta, T. Phase boundary near a magnetic percolation transition. Eur. Phys. J. B 94, 43 (2021). https://doi.org/10.1140/epjb/s10051-021-00056-4
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjb/s10051-021-00056-4