Skip to main content
SpringerLink
Log in

The transport mechanism of the integer quantum Hall effect

  • Regular Article
  • Published:
The European Physical Journal B Aims and scope Submit manuscript

Abstract

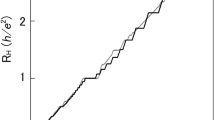
The integer quantum Hall effect (IQHE) is analysed using a mechanism of the electron transport in the form of semi-classic wave packages in this paper. Due to the confinement of the edges of a slab the Landau levels of electrons in a strong magnetic field go up at large wave-vectors to form energy bands. The slopes of the energy bands give the group velocities of electron wave packages and thus contribute to the current. Certain magnetic fields separate the electron transport in the slab into two branches with opposite and large wave vectors, which are localized at the two edges of the slab, respectively. In this case back scattering of electrons is prohibited due to the localization of these two branches. Thus the slab exhibits zero longitudinal resistance and plateaus of Hall resistance. When the Fermi level is sweeping over a Landau level at some magnetic fields, however, the electron waves locate around the central axis of the slab and overlap each other thus back scattering of electrons takes place frequently. Then longitudinal resistance appears and the Hall resistance goes up from one plateau to a new one. This transport mechanism is much clearer and more intuitive than the conventional explanations to the IQHE.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. K. von Klitzing et al., Phys. Rev. Lett. 45, 494 (1980)

    Article  ADS  Google Scholar 

  2. D.C. Tsui et al., Phys. Rev. Lett. 48, 1559 (1982)

    Article  ADS  Google Scholar 

  3. C.-Z. Chang et al., Science 340, 167 (2013)

    Article  ADS  Google Scholar 

  4. R.E. Prange, Phys. Rev. B 23, 5632 (1981)

    Article  Google Scholar 

  5. R.E. Prange, The Quantum Hall Effect, 2nd edn. (Springer-Verlag, 1990)

  6. Z.F. Ezawa, in Quantum Hall Effects: Field Theoretical Approach and Related Topics, 2nd edn. (Peking University Press, 2012), p. 182

  7. Ni Guangjiong, Chen Suqing, in Advanced Quantum Mechanics (in Chinese) (Fudan University Press, 2000), p. 310

  8. D.J. Thouless, M. Kohmoto, P. Nightingale, M. den Nijs, Phys. Rev. Lett. 49, 405 (1982)

    Article  ADS  Google Scholar 

  9. Q. Niu, D.J. Thouless, Y.-S. Wu, Phys. Rev. B 31, 3372 (1985)

    Article  ADS  MathSciNet  Google Scholar 

  10. Yasuhiro Hatsugai, Phys. Rev. B 48, 11851 (1993)

    Article  ADS  Google Scholar 

  11. S. Datta, in Electronic Transport in Mesoscopic systems (Cambridge University Press, 1995), p. 181

  12. Yan Shou Sheng, in Basis on solid state physics (in Chinese) (Peking University, 2003), p. 126

Download references

Author information

Authors and Affiliations

  1. Department of physics, School of Physics and Telecommunication Engineering, Guangdong Provincial Key Laboratory of Quantum Engineering and Quantum Materials, South China Normal University, Guangzhou, 510006, P.R. China

    Tan Hui & W. LiMing

  2. School of Physics, State Key Laboratory of Optoelectronic Material and Technology, Gangdong Province Key Laboratory of Display Material and Technology, Sun Yat-Sen University, Guangzhou, 510275, P.R. China

    Shi-Dong Liang

Authors
  1. Tan Hui
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. W. LiMing
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Shi-Dong Liang
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to W. LiMing.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Hui, T., LiMing, W. & Liang, SD. The transport mechanism of the integer quantum Hall effect. Eur. Phys. J. B 89, 257 (2016). https://doi.org/10.1140/epjb/e2016-70496-4

Download citation

  • Received:

  • Revised:

  • Published:

  • DOI: https://doi.org/10.1140/epjb/e2016-70496-4

Keywords

Search

Navigation