Statistical mechanics of Fofonoff flows in an oceanic basin

Abstract.

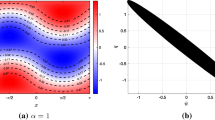
We study the minimization of potential enstrophy at fixed circulation and energy in an oceanic basin with arbitrary topography. For illustration, we consider a rectangular basin and a linear topography h = by which represents either a real bottom topography or the β-effect appropriate to oceanic situations. Our minimum enstrophy principle is motivated by different arguments of statistical mechanics reviewed in the article. It leads to steady states of the quasigeostrophic (QG) equations characterized by a linear relationship between potential vorticity q and stream function ψ. For low values of the energy, we recover Fofonoff flows [J. Mar. Res. 13, 254 (1954)] that display a strong westward jet. For large values of the energy, we obtain geometry induced phase transitions between monopoles and dipoles similar to those found by Chavanis and Sommeria [J. Fluid Mech. 314, 267 (1996)] in the absence of topography. In the presence of topography, we recover and confirm the results obtained by Venaille and Bouchet [Phys. Rev. Lett. 102, 104501 (2009)] using a different formalism. In addition, we introduce relaxation equations towards minimum potential enstrophy states and perform numerical simulations to illustrate the phase transitions in a rectangular oceanic basin with linear topography (or β-effect).