Skip to main content
SpringerLink
Log in

On the geometry of stiff knots

  • Interdisciplinary Physics
  • Published:
The European Physical Journal B Aims and scope Submit manuscript

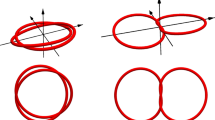
Abstract

We analyse the geometry of a thin knotted string with bending rigidity. Two types of geometric properties are investigated. First, following the approach of von der Mosel [H. von der Mosel, Asymptotic Anal. 18, 49 (1998)], we derive upper bounds for the multiplicity of crossings and braids. Then, using a general inequality for the length of 3D curves derived by Chakerian [G.D. Chakerian, Proc. of the American Math. Soc. 15, 886 (1964)], we analyze the size and confinement of a knot

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. L. Euler, Bousquet, Lausannae et Genevae 24, E65A (1744)

    Google Scholar 

  2. J. Langer, D.A. Singer, J. London Math. Soc. 30, 512 (1984)

    Article  MATH  MathSciNet  Google Scholar 

  3. R. Gallotti, O. Pierre-Louis, Phys. Rev. E 75, 031801 (2007)

    Article  MathSciNet  ADS  Google Scholar 

  4. B. Audoly, N. Clauvelin, S. Neukirch, Phys. Rev. Lett. 99, 164301 (2007)

    Article  ADS  Google Scholar 

  5. E. Guitter, E. Orlandini, J. Phys. A 32 1359 (1999); R. Metzler, A. Hanke, P.G. Dommersnes, Y. Kantor, M. Kardar, Phys. Rev. Lett. 88, 188101 (2002)

    Article  MATH  MathSciNet  ADS  Google Scholar 

  6. P.G. Dommersnes, Y. Kantor, M. Kardar, Phys. Rev. E 66, 031802 (2002)

    Article  ADS  Google Scholar 

  7. X.R. Bao, H.J. Lee, S.R. Quake, Phys. Rev. Lett. 91 265506 (2003)

    Article  ADS  Google Scholar 

  8. A.Y. Grosberg, Y. Rabin, Phys. Rev. Lett. 99, 217801 (2007)

    Article  ADS  Google Scholar 

  9. J.W. Milnor, Ann. Math. 52, 248 (1949)

    Article  MathSciNet  Google Scholar 

  10. H. von der Mosel, Asymptotic Anal. 18, 49 (1998)

    MATH  ADS  Google Scholar 

  11. G.D. Chakerian, Proc. of the American Math. Soc. 15, 886 (1964)

    Article  MATH  MathSciNet  Google Scholar 

  12. SA. Wasserman, NR. Cozzarelli, Science 232 951 (1986); D. Buck, E. Flapan, Knot Theory for Scientific Objects, OCAMI Studies (2007), p. 75

    Article  ADS  Google Scholar 

  13. J. O’Hara, Energy of knots and conformal geometry (World Scientific, Singapore, 2003); J. O’Hara, Ideal Knots (World Scientific, River Edge, NJ, 1998)

    MATH  Google Scholar 

  14. G. Buck, E.J. Rawdon Phys. Rev. E 70, 011803 (2004)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Laboratoire de Spectrométrie Physique, CNRS Univ. J. Fourier, BP87, Grenoble 1, 38402, Saint Martin d’Hères, France

    O. Pierre-Louis

  2. Rudolf Peierls Centre for Theoretical Physics, 1 Keble Road, Oxford, OX1 3NP, UK

    O. Pierre-Louis

Authors
  1. O. Pierre-Louis
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to O. Pierre-Louis.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pierre-Louis, O. On the geometry of stiff knots. Eur. Phys. J. B 71, 281–288 (2009). https://doi.org/10.1140/epjb/e2009-00301-6

Download citation

  • Received:

  • Revised:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjb/e2009-00301-6

PACS

Search

Navigation