Skip to main content
SpringerLink
Log in

Metastability and functional integration in anisotropically coupled map lattices

  • Statistical and Nonlinear Physics
  • Published:
The European Physical Journal B Aims and scope Submit manuscript

Abstract.

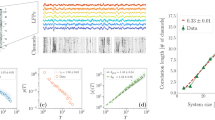
Metastability is a property of systems composed of many interacting parts wherein the parts exhibit simultaneously a tendency to function autonomously (local segregation) and a tendency to cooperate (global integration). We study anisotropically coupled map lattices and discover that for specific values of the coupling control parameters the entire system transits to a metastable regime. We show that this regime manifests a quasi-stable state in which the system can flexibly switch to another such state. We briefly discuss the relevance of our findings for information processing, functional integration, metastability in the brain, and phase transitions in complex systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  • R. Albert, A.L. Barabási, Rev. Mod. Phys. 74, 47 (2002)

    Article  ADS  MathSciNet  Google Scholar 

  • S. Boccaletti, V. Latora, Y. Moreno, M. Chavez, D. Hwang, Phys. Rep. 424, 175 (2006)

    Article  ADS  MathSciNet  Google Scholar 

  • A.S. Pikovsky, M.G. Rosenblum, J. Kurths, Synchronization (Cambridge Press, 2001)

  • J. Ito, K. Kaneko, Phys. Rev. E 67 (2003)

  • A. Venaille, P. Varona, M. Rabinovich, Phys. Rev. E 71, (2005)

  • T. Pereira, M. Baptista, J. Kurths, Eur. Phys. J. Special Topics 146, 155 (2007)

    Article  Google Scholar 

  • N. Masuda, K. Aihara, Biological Cybernetics 90, (2004)

  • M. Ivancheko, G. Osipov, V. Shalfeev, J. Kurths, Phys. Rev. Lett. 93, (2004)

  • G. Osipov, M. Ivancheko, J. Kurths, B. Hu, Phys. Rev. E 71 (2005)

  • C. Zhou, L. Zemanova, G. Zamora, C. Hilgetag, J. Kurths, Phys. Rev. Lett. 97, (2006)

  • L. Zemanova, C. Zhou, J. Kurths, Physica D 224, (2006)

  • C. Honey, R. Kotter, M. Breakspear, O. Sporns, Proc. Natl. Acad. Sci. USA 104, 10240 (2007)

    Article  ADS  Google Scholar 

  • S.L. Bressler, J.A. Kelso, Trends in Cognitive Science 5, 26 (2001)

    Article  Google Scholar 

  • A. Fingelkurts, A. Fingelkurts, Int. J. Neurosc. 114, 843 (2004)

    Article  Google Scholar 

  • M.G. Werner, Proceedings The Evolution of Human Cognition and Neuroscience (Les Treilles, Provence, France, 2006)

  • K. Kaneko, Prog. Theor. Phys. 72, 480 (1984)

    Article  MATH  ADS  Google Scholar 

  • Y. Dobyns, H. Atmanspacher, Chaos, Solitons and Fractals 28, 755 (2006)

    Article  MATH  MathSciNet  Google Scholar 

  • W. McGill, IEEE Trans. Inform. Theory 4, 93 (1954)

    Article  MathSciNet  Google Scholar 

  • G. Tononi, O. Sporns, G.M. Edelman, Proc. Natl. Acad. Sci. USA 91, 5033 (1994)

    Article  ADS  Google Scholar 

  • E. Schneidman, S. Still, M.J. Berry, W. Bialek, Phys. Rev. Lett. 91, 238701 (2003)

    Article  ADS  Google Scholar 

  • G. Tononi, O. Sporns, G.M. Edelman, Proc. Natl. Acad. Sci. USA 93, 3422 (1996)

    Article  ADS  Google Scholar 

  • F.C. Hoppensteadt, E.M. Izhikevich, Phys. Rev. E 62, 4010 (2000)

    Article  ADS  Google Scholar 

  • G. Tononi, O. Sporns, BMC Neurosc. 4, 31 (2003)

    Article  Google Scholar 

  • K. Doya, Neural Network 15, 495 (2002)

    Article  ADS  Google Scholar 

  • S. Dehaene, J. Changeux, Plos 3, 1 (2005)

    Article  Google Scholar 

  • E. Izhikevich, G. Edelman, PNAS 105, 3593 (2008)

    Article  ADS  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. ERATO Synergistic Intelligence Project, JST, The University of Tokyo, 113-8656, Tokyo, Japan

    A. Pitti, M. Lungarella & Y. Kuniyoshi

  2. Artificial Intelligence Lab, University of Zurich, 8050, Zurich, Switzerland

    M. Lungarella

  3. ISI Laboratory, Dept. of Mechano-Informatics, The University of Tokyo, 113-8656, Tokyo, Japan

    Y. Kuniyoshi

Authors
  1. A. Pitti
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. M. Lungarella
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Y. Kuniyoshi
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Pitti.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pitti, A., Lungarella, M. & Kuniyoshi, Y. Metastability and functional integration in anisotropically coupled map lattices. Eur. Phys. J. B 63, 239–243 (2008). https://doi.org/10.1140/epjb/e2008-00238-2

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjb/e2008-00238-2

PACS.

Search

Navigation