Generalization of a nonlinear friction relation for a dimer sliding on a periodic substrate

Abstract.

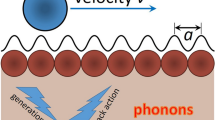
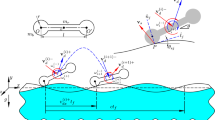
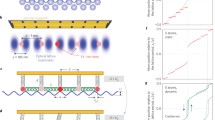
An atomic cluster moving along a solid surface can undergo dissipation of its translational energy through a direct mode, involving the coupling of the center-of-mass motion to thermal excitations of the substrate, and an indirect mode, due to damping of the internal motion of the cluster, to which the center-of-mass motion can be coupled as a result of surface potential. Focussing only on the less well understood indirect mode, on the basis of numerical solutions, we present, departures from a recently reported simple relationship between the force and velocity of nonlinear friction. A generalization of the analytic considerations that earlier led to that relationship is carried out and shown to explain the departures satisfactorily. Our generalization treats for the system considered (dimer sliding over a periodic substrate) the complete dependence on several of the key parameters, specifically internal dissipation, natural frequency, substrate corrugation, and length ratio. Further predictions from our generalizations are found to agree with new simulations. The system analyzed is relevant to nanostructures moving over crystal surfaces.