Skip to main content
SpringerLink
Log in

Chebyshev expansion approach to the AC conductivity of the Anderson model

  • Published:
The European Physical Journal B - Condensed Matter and Complex Systems Aims and scope Submit manuscript

Abstract.

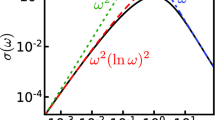
We propose an advanced Chebyshev expansion method for the numerical calculation of linear response functions at finite temperature. Its high stability and the small required resources allow for a comprehensive study of the optical conductivity \(\sigma(\omega)\) of non-interacting electrons in a random potential (Anderson model) on large three-dimensional clusters. For low frequency the data follows the analytically expected power-law behaviour with an exponent that depends on disorder and has its minimum near the metal-insulator transition, where also the extrapolated DC conductivity continuously goes to zero. In view of the general applicability of the Chebyshev approach we briefly discuss its formulation for interacting quantum systems.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. P.W. Anderson, Phys. Rev. 109, 1492 (1958)

    Article  ADS  Google Scholar 

  2. D.J. Thouless, Physics Reports 13, 93 (1974); P.A. Lee, T.V. Ramakrishnan, Rev. Mod. Phys. 57, 287 (1985); B. Kramer, A. Mac Kinnon, Rep. Prog. Phys. 56, 1469 (1993)

    Article  ADS  Google Scholar 

  3. E. Abrahams et al. , Phys. Rev. Lett. 42, 673 (1979)

    Article  ADS  Google Scholar 

  4. K.B. Efetov, Adv. Phys. 32, 53 (1983)

    Article  MathSciNet  ADS  Google Scholar 

  5. K. Slevin, T. Ohtsuki, Phys. Rev. Lett. 82, 382 (1999)

    Article  ADS  Google Scholar 

  6. A. Mac Kinnon, B. Kramer, Z. Phys. B 53, 1 (1983)

    Article  ADS  Google Scholar 

  7. F.J. Wegner, Z. Phys. B 25, 327 (1976)

    Article  ADS  Google Scholar 

  8. K.B. Efetov, O. Viehweger, Phys. Rev. B 45, 11546 (1992)

    Article  ADS  Google Scholar 

  9. M.R. Zirnbauer, Phys. Rev. B 34, 6394 (1986)

    Article  MathSciNet  ADS  Google Scholar 

  10. B. Shapiro, E. Abrahams, Phys. Rev. B 24, 4889 (1981)

    Article  ADS  Google Scholar 

  11. R. Oppermann, F. Wegner, Z. Phys. B 34, 327 (1979)

    Article  ADS  Google Scholar 

  12. B. Shapiro, Phys. Rev. B 25, 4266 (1982)

    Article  ADS  Google Scholar 

  13. N.F. Mott, Adv. Phys. 16, 49 (1967)

    Article  ADS  Google Scholar 

  14. P. Lambrianides, H.B. Shore, Phys. Rev. B 50, 7268 (1994)

    Article  ADS  Google Scholar 

  15. H. Shima, T. Nakayama, Phys. Rev. B 60, 14066 (1999)

    Article  ADS  Google Scholar 

  16. R.C. Albers, J.E. Gubernatis, Phys. Rev. B 17, 4487 (1978)

    Article  ADS  Google Scholar 

  17. A. Singh, W.L. McMillan, J. Phys. C 18, 2097 (1985)

    Article  ADS  Google Scholar 

  18. M. Hwang, A. Gonis, A.J. Freeman, Phys. Rev. B 35, 8974 (1987)

    Article  ADS  Google Scholar 

  19. T. Iitaka, in High Performance Computing in RIKEN 1997, Vol. 19 of RIKEN Review (Inst. Phys. Chem. Res. (RIKEN), Japan, 1998), pp. 136-143

  20. R.N. Silver, H. Röder, Int. J. Mod. Phys. C 5, 935(1994)

    Article  Google Scholar 

  21. R.N. Silver et al. , J. Comp. Phys. 124, 115 (1996)

    Article  MathSciNet  ADS  MATH  Google Scholar 

  22. T. Iitaka, T. Ebisuzaki, Phys. Rev. Lett. 90, 047203(2003)

    Article  ADS  Google Scholar 

  23. L.-W. Wang, A. Zunger, Phys. Rev. Lett. 73, 1039 (1994); L.-W. Wang, Phys. Rev. B 49, 10154 (1994)

    Article  ADS  Google Scholar 

  24. R. Haydock, V. Heine, M.J. Kelly, J. Phys. C 5, 2845 (1972)

    Article  ADS  Google Scholar 

  25. J. Jaklič, P. Prelovšek, Phys. Rev. B 49, 5065 (1994)

    Article  ADS  Google Scholar 

  26. M. Aichhorn et al. , Phys. Rev. B 67, 161103 (2003)

    Article  ADS  Google Scholar 

  27. More details to be published elsewhere

Download references

Author information

Authors and Affiliations

  1. School of Physics, The University of New South Wales, NSW 2052, Sydney, Australia

    A. Weisse

Authors
  1. A. Weisse
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to A. Weisse.

Additional information

Received: 6 June 2004, Published online: 12 August 2004

PACS:

78.20.Bh Theory, models, and numerical simulation - 72.15.Rn Localisation effects (Anderson or weak localisation) - 05.60.Gg Quantum transport

Rights and permissions

Reprints and permissions

About this article

Cite this article

Weisse, A. Chebyshev expansion approach to the AC conductivity of the Anderson model. Eur. Phys. J. B 40, 125–128 (2004). https://doi.org/10.1140/epjb/e2004-00250-6

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjb/e2004-00250-6

Keywords

Search

Navigation