Skip to main content
SpringerLink
Log in

On the number of contacts of two polymer chains situated on fractal structures

  • Published:
The European Physical Journal B - Condensed Matter and Complex Systems Aims and scope Submit manuscript

Abstract.

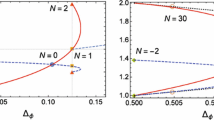
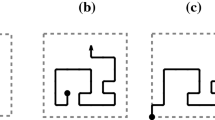
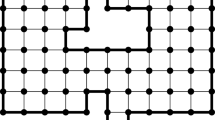
We study the critical behavior of the number of monomer-monomer contacts for two polymers in a good solvent. Polymers are modeled by two self-avoiding walks situated on fractals that belong to the checkerboard (CB) and X family. Each member of a family is labeled by an odd integer b, \(3\le b\le\infty\). By applying the exact Renormalization Group (RG) method, we establish the relevant phase diagrams whereby we calculate the contact critical exponents \(\varphi\) (for the CB and X fractals with b = 5 and b = 7). The critical exponent \(\varphi\) is associated with power law of the number of sites at which the two polymers are touching each other.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. M. Rubinstein, R. Colby, Polymer Physics (Oxford University Press, New York, 2003)

  2. C. Vanderzande, Lattice Models of Polymers (Cambridge University Press, Cambridge, 1998)

  3. E. Bouchaud, J. Vannimenus, J. Phys. A 50, 2931 (1989)

    Google Scholar 

  4. A. Lapp, M. Mottin, D. Broseta, L. Leibler, J. Phys. II France 2, 1247 (1992)

    Article  Google Scholar 

  5. N. Posharnowa, A. Schneider, M. Wünsch, V. Kuleznew, B.A. Wolf, J. Chem. Phys. 115, 9536 (2001)

    Article  Google Scholar 

  6. K. Kumeta, I. Nagashima, S. Matsui, K. Mizoguchi, J. Appl. Polym. Sci. 90, 2420 (2003)

    Article  Google Scholar 

  7. P.G. de Gennes, J. Phys. Lett. 40, 69 (1979)

    Google Scholar 

  8. Ch. Kappeler, L. Schäfer, T. Fukuda, Macromolecules 24, 2715 (1991)

    Google Scholar 

  9. M. Benmouna, T.A. Vilgis, M. Daoud, M. Benhamou, Macromolecules 27, 1172 (1994)

    Google Scholar 

  10. L. Schäfer, Ch. Kappeler, J. Phys. France 46, 1853 (1985)

    Google Scholar 

  11. M. Benhamou, A. Derouiche, A. Bettachy, J. Chem. Phys. 106, 2513 (1997)

    Article  Google Scholar 

  12. S. Müller, L. Schäfer, Eur. Phys. J. B 2, 351 (1998)

    Article  Google Scholar 

  13. T.A.S. Haddad, R.F.S. Andrade, S.R. Salinas, J. Phys. A 37, 1499 (2004)

    Article  MATH  Google Scholar 

  14. K.F. Freed, J. Phys. A 18, 871 (1985)

    Article  MathSciNet  Google Scholar 

  15. A. Sariban, K. Binder, J. Chem. Phys. 86, 5859 (1987)

    Article  Google Scholar 

  16. P. Leoni, C. Vanderzande, L. Vandeurzen, J. Phys. A 34, 9777 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  17. E. Orlandini, F. Seno, A.L. Stella, Phys. Rev. Lett. 84, 294 (2000)

    Article  Google Scholar 

  18. M. Baiesi, E. Carlon, E. Orlandini, A.L. Stella, Phys. Rev. E 63, 041801 (2001)

    Article  Google Scholar 

  19. E. Orlandini, S.M. Bhattacharjee, D. Marenduzzo, A. Maritan, F. Seno, J. Phys. A 34, L751 (2001)

  20. D. Marenduzzo, S.M. Bhattacharjee, A. Maritan, E. Orlandini, F. Seno, Phys. Rev. Lett. 88, 028102 (2002)

    Article  Google Scholar 

  21. Y. Kafri, D. Mukamel, L. Peliti, Eur. Phys. J. B 27, 135 (2002)

    Article  Google Scholar 

  22. M. Baiesi, E. Carlon, E. Orlandini, A.L. Stella, Eur. Phys. J. B 29, 129 (2002)

    Article  Google Scholar 

  23. S. Kumar, Y. Singh, J. Phys. A 26, L987 (1993)

  24. S. Kumar, Y. Singh, J. Stat. Phys. 89, 981 (1997)

    MATH  Google Scholar 

  25. I. Živić, S. Milošević, J. Phys. A 31, 1365 (1998)

    Google Scholar 

  26. S. Kumar, Physica A 292, 422 (2001)

    Article  MathSciNet  MATH  Google Scholar 

  27. S. Elezović-Hadžić, S. Milošević, J. Phys. A 25, 4095 (1992)

    MathSciNet  Google Scholar 

  28. S. Milošević, I. Živić, V. Miljković, Phys. Rev. E 55, 5671 (1997)

    Article  Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Faculty of Physics, University of Belgrade, P.O. Box 368, 11001, Belgrade, Serbia

    V. Miljković & S. Milošević

  2. Faculty of Natural Sciences and Mathematics, University of Kragujevac, 34000, Kragujevac, Serbia

    I. Živić

Authors
  1. V. Miljković
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. I. Živić
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. S. Milošević
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to S. Milošević.

Additional information

Received: 12 March 2004, Published online: 3 August 2004

PACS:

64.60.Ak Renormalization-group, fractal, and percolation studies of phase transitions - 36.20.Ey Conformation (statistics and dynamics)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Miljković, V., Živić, I. & Milošević, S. On the number of contacts of two polymer chains situated on fractal structures. Eur. Phys. J. B 40, 55–61 (2004). https://doi.org/10.1140/epjb/e2004-00238-2

Download citation

  • Issue Date:

  • DOI: https://doi.org/10.1140/epjb/e2004-00238-2

Keywords

Search

Navigation