Skip to main content
SpringerLink
Log in

Thermohydrodynamics of supercritical fluids in the presence of temperature heterogeneities

  • Published:
Russian Journal of Physical Chemistry B Aims and scope Submit manuscript

Abstract

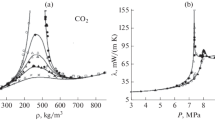
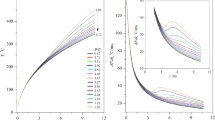
Main regularities of heat gravitational convection are considered near the thermodynamic critical point. Special physical properties of supercritical fluids (strong increase of heat capacity at constant pressure and coefficients of heat extension and isothermal compressibility, convergence to zero of the coefficient of thermal diffusivity upon approximation to a critical point) lead to the features of convective flow and heat transfer. Hydrodynamic behavior of supercritical fluids is characterized by intensification of internal movement, decrease in the spatial scale of convection, formation of a piston effect, temporal multiresolution of dynamic and heat processes, and the effect of stratification.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. D. Yu. Zalepugin, N. A. Til’kunova, I. V. Chernyshova, and V. S. Polyakov, Sverkhkrit. Fluidy: Teor. Prakt. 1(1), 27 (2006).

    Google Scholar 

  2. A. Z. Patashinskii and V. L. Pokrovskii, Fluctuation Theory of Phase Transitions (Nauka, Moscow, 1975) [in Russian].

    Google Scholar 

  3. M. A. Anisimov, The Critical Phenomena in Liquids and Liquid Crystals (Nauka, Moscow, 1987) [in Russian].

    Google Scholar 

  4. V. I. Polezhaev and E. B. Soboleva, Priroda (Moscow, Russ. Fed.), No. 10, 17 (2003).

    Google Scholar 

  5. V. M. Emel’yanov, A. A. Gorbunov, A. K. Lednev, and S. A. Nikitin, Sverkhkrit. Fluidy: Teor. Prakt. 4(2), 71 (2009).

    Google Scholar 

  6. A. V. Zyuzgin, A. I. Ivanov, V. I. Polezhaev, G. F. Putin, and E. B. Soboleva, Kosm. Issled. 39(2), 188 (2001).

    Google Scholar 

  7. V. I. Polezhaev and E. B. Soboleva, Izv. Akad. Nauk, Mekh. Zhidk. Gasa, No. 3, 70 (2000).

    Google Scholar 

  8. J. C. Dunn and H. C. Hardee, J. Volcanol. Geotherm. Res. 11, 189 (1981).

    Article  Google Scholar 

  9. N. V. Koronovskii, Soros. Obrazov. Zh., No. 10, 55 (1999).

    Google Scholar 

  10. E. B. Soboleva, Ann. N.Y. Acad. Sci. 1161, 117 (2009).

    Article  CAS  Google Scholar 

  11. V. I. Polezhaev and E. B. Soboleva, Izv. Akad. Nauk, Mekh. Zhidk. Gasa, No. 2, 48 (2005).

    Google Scholar 

  12. E. B. Soboleva, Eprint. Fluid Dynamics (2010). arXiv: 1001.4139v1 [physics.flu-dyn]

    Google Scholar 

  13. A. B. Kogan and H. Meyer, Phys. Rev. E 63, 056310 (2001).

    Article  CAS  Google Scholar 

  14. D. A. Nield and A. Beian, Convection in Porous Media (Springer, New York, 1992).

    Book  Google Scholar 

  15. E. B. Soboleva, Izv. Akad. Nauk, Mekh. Zhidk. Gasa, No. 2, 57 (2008).

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Ishlinskii Institute for Problems in Mechanics, Moscow, Russia

    E. B. Soboleva

Authors
  1. E. B. Soboleva
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. B. Soboleva.

Additional information

Original Russian Text © E.B. Soboleva, 2013, published in Sverkhkriticheskie Flyuidy: Teoriya i Praktika, 2013, Vol. 8, No. 4, pp. 62–77.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Soboleva, E.B. Thermohydrodynamics of supercritical fluids in the presence of temperature heterogeneities. Russ. J. Phys. Chem. B 8, 1009–1018 (2014). https://doi.org/10.1134/S1990793114080132

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1990793114080132

Keywords

Search

Navigation