Skip to main content
SpringerLink
Log in

The fluctuation kinetics of formation of nanoparticles: Particle-size distribution

  • Chemical Physics of Nanomaterials
  • Published:
Russian Journal of Physical Chemistry B Aims and scope Submit manuscript

Abstract

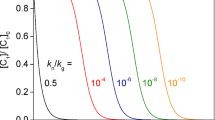
A stochastic simulation of the growth of particles on a uniform cubic lattice was performed by the Monte Carlo method. Changes in the width of the distribution (M w /M n ) as the size of particles increased were extremal in character. Distribution narrowing occurred much more slowly than in classic polymerization. An empirical equation relating the number of free vacancies of a growing particle and its mean size was obtained. The introduction of a stabilizer deactivating free vacancies of a growing particle caused the appearance of a critical phenomenon. At stabilizer concentrations higher than critical, large-sized particles could not form. At stabilizer concentrations close to critical, the particle-size distribution was bimodal. This resulted in an anomalously larger distribution width.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Similar content being viewed by others

References

  1. I. P. Suzdalev and P. I. Suzdalev, Usp. Khim. 70, 203 (2001).

    Google Scholar 

  2. D. Frenkel and B. Smit, Understanding Molecular Simulation: From Algorithms to Applications (Academic, San Diego, 2002).

    Google Scholar 

  3. Ya. B. Zel’dovich and A. S. Mikhailov, Usp. Fiz. Nauk 153, 469 (1987) [Sov. Phys. Usp. 30, 977 (1987)].

    Article  Google Scholar 

  4. R. F. Khairutdinov, Usp. Khim. 67, 125 (1998).

    CAS  Google Scholar 

  5. Physico-Chemical Phenomena in thin Films and Solid Surfaces, Ed. by L. I. Trakhtenberg, S. H. Lin, and O. J. Ileghusi (Elsevier, New York, 2007).

    Google Scholar 

  6. V. P. Zhdano and V. B. Kasemo, Chem. Phys. Lett. 460, 158 (2008).

    Article  Google Scholar 

  7. A. F. Shestakov, V. N. Solov’ev, V. V. Zagorskii, and G. B. Sergeev, Zh. Fiz. Khim. 68, 155 (1994).

    CAS  Google Scholar 

  8. E. V. Bystritskaya and O. N. Karpukhin, Khim. Fiz. 28(10), 91 (2009) [Russ. J. Phys. Chem. B 28, 851 (2009)].

    CAS  Google Scholar 

  9. L. Rodrigues-Sanchez, M. L. Blanko, and M. A. Lopez-Quintela, J. Phys. Chem. B 104, 9683 (2000).

    Article  Google Scholar 

  10. F. Grohn, B. J. Bauer, Y. A. Akpalu, C. L. Jackson, and E. J. Amis, Macromolecules 33, 6042 (2000).

    Article  Google Scholar 

  11. P. Mendes, Comp. Appl. Biosci. 9, 563 (1993).

    CAS  Google Scholar 

  12. Al. Al. Berlin and S. A. Wolfson, Kinetic Method on the Synthesis of Polymers (Khimiya, Moscow, 1973) [in Russian].

    Google Scholar 

Download references

Author information

Authors and Affiliations

  1. Semenov Institute of Chemical Physics, Russian Academy of Sciences, ul. Kosygina 4, Moscow, Russia

    E. V. Bystritskaya & O. N. Karpukhin

Authors
  1. E. V. Bystritskaya
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. O. N. Karpukhin
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to E. V. Bystritskaya.

Additional information

Original Russian Text © E.V. Bystritskaya, O.N. Karpukhin, 2010, published in Khimicheskaya Fizika, 2010, Vol. 29, No. 6, pp. 92–95.

Rights and permissions

Reprints and permissions

About this article

Cite this article

Bystritskaya, E.V., Karpukhin, O.N. The fluctuation kinetics of formation of nanoparticles: Particle-size distribution. Russ. J. Phys. Chem. B 4, 517–520 (2010). https://doi.org/10.1134/S1990793110030243

Download citation

  • Received:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1134/S1990793110030243

Keywords

Search

Navigation