Parallel machines scheduling with time-dependent deterioration, using meta-heuristic algorithms

Abstract

In this paper, we consider the identical parallel machines scheduling problem with exponential time-dependent deterioration. The meaning of time-dependent deterioration is that the processing time of a job is not a constant and depends on the scheduled activities. In other words, when a job is processed later, it needs more processing time compared to the jobs processed earlier. The main purpose is to minimize the makespan. To reach this aim, we developed a mixed integer programming formulation for the problem. We solved problem in small scale using GAMS software, while due to the fact that in larger scales the aforesaid case is a complex and intricate optimized problem which is NP-hard, it is not possible to solve it by standard calculating techniques (in logical calculating times); we applied the meta-heuristic genetic algorithm, simulating annealing and artificial immune system, and their performance has been evaluated. In the end, we showed that solving the problem in small scale, with the meta-heuristic algorithms (GA, SA, and AIS) equals the optimal solution (GAMS), And on a large scale, at a time of approximately equal solution, meta-heuristic algorithm simulating annealing, provides a more optimal solution.

1 Introduction

The basic model of scheduling theory assumes that the processing time of a job is predetermined and constant. However, this assumption may not always be true because of the tools and machinery face deterioration which decreases the machining quality over the time [6]. Parts with turning process or cutting process are another practical example in this field. For example, there are some products that need to be processed by a cutting tool. Because of wear of the cutting tool, the time required for processing a single product increases with respect to the processing time of products already executed [32, 36].

In recent years, the phenomenon known as deterioration has been considered by many researchers, after the pioneering works of Gupta et al. [12] on scheduling models in which they focused on single-machine scheduling with deteriorating jobs and introduced the processing time of a job as the polynomial function of its setup time. Alidaee and Womer [1] have classified scheduling models with deteriorating jobs into three types of linear deterioration, piecewise linear deterioration and nonlinear deterioration. In these types, the actual job processing time directly or indirectly depends on the setup time. In the following, we will review the literature on the related studies.

Chen [5] and Woeginger [37] studied the scheduling problem of deteriorating jobs with the objective function of the jobs with preemption assuming that the due dates are the same. To solve the problem, they proposed the dynamic programming algorithm with the complexity $O \left( {n^{2} } \right)$ and $O \left( {n^{3} } \right)$, respectively. In their research, Ji et al. [15] focused on the makespan and the total completion time of deteriorating jobs on machine with the availability constraint while they consider non-resumable case. They showed that both problems are non-deterministic polynomial hard (NP-hard) and present pseudo polynomial time optimal algorithms to solve them. Furthermore, for the makespan problem, present an optimal approximation algorithm and for the total completion time problem, provide a heuristic and evaluate its efficiency by computational experiments. Wang et al. [33] stated that flow shop scheduling with the objective of minimizing makespan in the basic form is NP-hard. They focused on the aforesaid problem in two sections of their study. They first examined it in four different forms and put them in an optimal order. In the second part, a Branch and Bound (B&B) approach was employed to solve the cases with 14 jobs. Moreover, they proposed a heuristic two-stage algorithm which was proved to be effective. Lee and Wu [19] considered the scheduling problem of deteriorating jobs on parallel machines with machines availability constraint. They proposed a new algorithm using the LDR (largest deterioration rate first) rule and the idea of the MULTIFIT heuristic proposed by Coffman et al. [8], for the makespan problem. Mosheiov [23] investigated the makespan in the single-machine cases in which the actual processing time of each job is defined by an exponential function of its position. He also showed that an optimal schedule is a V-shaped schedule in terms of the basic or normal processing times of jobs. In their survey, Lee et al. [20] assumed that the actual processing time of a job in position $r$ is dependent on the processing time of the prior job $r - 1$. They demonstrated that longest processing time first rule (LPT) would optimize total completion time problem in a single machine assuming that the deterioration coefficient was between 0 and 1. Ng et al. [24] considered a two-machine flow shop scheduling problem to minimize the total completion time with proportional linear deterioration. They derived it from several dominance properties, some lower bounds, and an initial upper bound, then applied them in an assumed branch-and-bound algorithm to search for the optimal solution. Wang et al. [35] considered the single-machine scheduling problem with learning effect of a time-dependent deterioration. They formulated the model and proposed a mixed integer programming formulation (MIP) for the aforesaid problem and applied the shortest processing time (SPT) rule as a heuristic algorithm for general cases and analyzed its worst-case error bound. Two heuristic algorithms HA1 (is adopted from Kanet [17] idea) and HA2 (Proposed algorithm according to the HA1) which utilize the V-shaped property for the problem of the smallest total completion time were also proposed. Joo and Kim [16] considered the time-dependent deterioration problem and some scheduling problems with rate-modifying activities (i.e. getting recovered to a normal processing time known as RMA). They used a mathematical model to find an optimal solution for minimizing the makespan. Also they considered genetic algorithm with the special character (GA-SC), a genetic algorithm using chromosomes with double string (GA-DS) and a genetic algorithm compounded with dispatching rule (GA-DR). They finally showed that GA-DR provides the highest quality performance, in both effectiveness and efficiency. Torres [31] considered an unrelated parallel machine scheduling problem with time-dependent deterioration given that single-machine problem could be solved in polynomial time. The problem is NP-hard when the scale of the problem grows. They employed a simulated annealing (SA) meta-heuristic algorithm to minimize the total completion time and showed the effectiveness of this algorithm by solving a large number of benchmark instances. Chung and Kim [7] considered a hybrid genetic algorithm (GA) together with a heuristic algorithm for single-machine scheduling problem with time-dependent deterioration and rate-modifying activities. First, they wrote a mixed integer program for optimizing the total completion and applied the problem in scales greater than the hybrid genetic scale with chromosome (GA-SC, GA-DS) and a heuristic solution. They showed that the obtained results are precisely similar.

Shin et al. [28] presented a heuristic and tabu search (TS) algorithm for the problem of single-machine scheduling with sequence-dependent setup time and the release time and the objective function with the aim of minimizing the maximum lateness. Stecco et al. [29] developed a tabu search algorithm for the time-dependent and sequence-dependent single-machine scheduling problem. Bahalke et al. [2] proposed some hybrid meta-heuristic algorithm for single-machine scheduling with sequence dependent on setup time and job deterioration to minimize the makespan. Rabani et al. [26] considered a new hybrid meta-heuristic approach to optimization of parallel machine scheduling problem with human resiliency engineering. They proposed a hybrid meta-heuristic algorithm GA and SA for the problem of non-identical parallel machines and stated that hybrid approach is better than other approaches. Salehi Mir et al. [27] considered scheduling parallel machine problem under general effects of deterioration and learning with past-sequence-dependent setup time with heuristic and meta-heuristic approaches. For solving this problem, they proposed a mixed integer programming model, then used three methodologies including a heuristic algorithm (HA), a genetic algorithm (GA) and an ant colony optimization (ACO), with a new stochastic result-oriented strategy. They finally showed that the proposed algorithm provides the optimal solution to the small-size problems and the ACO meta-heuristic algorithm statistically better than HA and GA. Cheng et al. [6] studied a class of machines scheduling problems in which the processing time of a job dependent on the setup time. They classified the scheduling problem with different types of time-dependent deterioration and provided a framework for the models of classic problems that had been generalized from the theory of classic scheduling. Wang et al. [32, 36] considered the single-machine scheduling problems with deterioration jobs and group technology assumption. They showed that minimizing the makespan in polynomial time can be solved if the total linear deterioration and group technology are regarded to be simultaneous actions. Wang et al. [34] considered the sing-machine problems of scheduling jobs with start time increasing processing times. The two objectives of the scheduling problems are to minimize the makespan and the total weighted completion time, respectively. Under the assumption of series–parallel graph precedence constraints, they proved that the problems were polynomially solvable.

In the present paper, we have considered the scheduling problem of minimizing the maximum completion time ($C_{\max }$) in parallel and identical machines with a time-dependent deterioration proposed in the studies of Wang et al. [35]. They calculated the actual processing time of the job using the previous scheduled jobs. One of the aims of this study that not observed in previous studies is that of applying scheduling with a time-dependent deterioration Model (in the study of Wang et al. [35]) in the identical parallel machines environment. We developed a mixed integer programming formulation for the problem, then solved it with three meta-heuristic algorithms (GA), (SA) and artificial immune systems (AIS) for the first time and compared the results obtained.

This paper has been organized as follows: in Sect. 2, we wrote a mixed integer programming model. In Sect. 3, as the problem $P_{m} ||C_{\max }$ is strongly NP-hard for higher numbers of m [11], we solved the problem in a larger scale using the meta-heuristic algorithms (genetic, simulating annealing, artificial immune system) and evaluated their performance. The final section dealt with concluding remarks.

2 Model formulation

Consider the identical parallel machines problem. There is a set of n jobs $i = \left\{ {i_{1} ,i_{2} , \ldots ,i_{n} } \right\}$ where all jobs are available for processing at time 0 and setup time = 0. The machine can handle one job at a time and preemption is not allowed. Each job is associated with a normal processing time $p_{i }$ and the normal processing time of a job if scheduled at the rth position in a sequence $p_{\left[ r \right]} .$ Suppose that the $p_{ir}$ is the processing time of job $i$ when it is scheduled at the position $r$ in a sequence. Like the study of Wang et al. [35], we consider a time-dependent deterioration model using Eq. (1):

$$p_{ir} = p_{i} \left( {1 + p_{\left[ 1 \right]} + p_{\left[ 2 \right]} + \cdots + p_{{\left[ {r - 1} \right]}} } \right)^{a}$$

(1)

In this relation, the actual processing time in position $r$ depends on the basic processing time of the previous scheduled activity $r - 1$. Where $a \ge 0$ is the deterioration index.

According to the three-field notation scheme $\alpha \left| { \beta } \right| \gamma$ introduced by Graham et al. [13], we show the problem considered in this research as $P_{m} |p_{ir} = p_{i} \left( {1 + p_{\left[ 1 \right]} + p_{\left[ 2 \right]} + \ldots + p_{{\left[ {r - 1} \right]}} } \right)^{a} ,\,\, 0 < a < 1|C_{\max } .$

Notations

$m$: The number of available machines.

$n$: The number of jobs which need to be scheduled.

$j$: The index of machines, $j = 1, \ldots ,m$.

$i$: The index of jobs, $i = 1, \ldots , n$.

$r$: The index of the position of each job, $r = 1, \ldots ,n$.

Parameters

$P_{i}$: The normal processing time of job $i$.

$t_{j}$: The setup time of the first scheduled job in machine $j$.

$\alpha$: The deterioration index.

Decision variables

$X_{irj}$: Equals 1 when job $i$ is done in position $r$ on machine $j$. Otherwise, it is 0.

$P_{\left[ r \right]j}$: The actual processing time of the job scheduled in position $r$ on machine $j$.

$C_{\left[ r \right]j}$: The actual completion time the job scheduled in position $r$ on machine $j$.

$C_{max}$: The total completion time (completion time of the machine with the maximum load,$C_{max} = \max \{ C | j = 1,2, \ldots ,n\}$).

Based on the parameters and decision variables, a mixed integer programming process can be formulated.

Constraints

Constraint (2) stipulates that each job must be processed.

$$\mathop \sum \limits_{j = 1}^{m} \mathop \sum \limits_{r = 1}^{n} X_{irj} = 1\quad \forall i = 1, \ldots , n.$$

(2)

Constraint (3) guarantees that just one job be processed in any position on any machine.

$$\mathop \sum \limits_{i = 1}^{n} X_{irj} \le 1\quad \forall j = 1, \ldots ,m; r = 1, \ldots ,n.$$

(3)

Constraint (4) guarantees that immediately after each job, just one of the remaining jobs can be done.

$$X_{irj} + \mathop \sum \limits_{l = 1,l \ne i}^{n} X_{lr + 1j} \le 2\quad \forall i = 1, \ldots ,n; j = 1, \ldots ,m; r = 1, \ldots ,n - 1.$$

(4)

Constraint (5) shows that when job $i$ is not in its initial position, another job must be done immediately before job $i$.

$$X_{i,r + 1,j} \le \mathop \sum \limits_{l = 1,l \ne i}^{n} X_{lrj} \quad \forall i = 1, \ldots ,n; j = 1, \ldots ,m; r = 1, \ldots ,n - 1.$$

(5)

Constraint (6) shows the processing time of the job scheduled in the first position on machine $j$.

$$P_{\left[ 1 \right]j} = \mathop \sum \limits_{i = 1}^{n} \left( {P_{i} } \right)X_{i,1,j} \quad \forall j = 1, \ldots ,m.$$

(6)

Constraint (7) shows the processing time of the job scheduled in position $r$ on machine $j$.

$$P_{\left[ r \right]j} = \mathop \sum \limits_{i = 1}^{n} \left( {P_{i} } \right)X_{i,r,j} \quad \forall j = 1, \ldots ,m; r = 2, \ldots ,n.$$

(7)

Constraints (8) and (9) show the actual completion time of the job scheduled in the first and rth position on machine $j$.

$$C_{\left[ 1 \right]j} = t_{j} + P_{\left[ 1 \right]j} \quad \forall j = 1, \ldots ,m,$$

(8)

$$C_{\left[ r \right]j} = C_{{\left[ {r - 1} \right]j}} + P_{\left[ r \right]j} \left( {1 + \mathop \sum \limits_{i = 1}^{r - 1} P_{\left[ i \right]j} } \right)^{\alpha } \quad \forall j = 1, \ldots ,m; r = 2,...,n.$$

(9)

Constraint (10) shows the upper limit $C_{\max}$.

$$C_{\left[ r \right]j} \le C_{\max } \quad \forall j = 1, \ldots ,m; r = 1, \ldots ,n.$$

(10)

Constraint (11) shows the range decision variables.

$$X_{irj} = 0,1,P_{\left[ r \right]j} ,C_{\left[ r \right]j} ,C_{\max } \ge 0\quad \forall i = 1, \ldots ,n; j = 1, \ldots ,m; r = 1, \ldots ,n.$$

(11)

Objective function

The objective of the scheduling problem in parallel machines is to minimize the completion time of the machine with the maximum load which is shown in Eq. (12).

$$Min C_{\max }$$

(12)

3 Meta-heuristic algorithms

We propose three effective and efficient meta-heuristic algorithms, because the mixed integer programming model is not suitable for the problems over 10 jobs because of the long computation time [16]. The parallel machines scheduling with exponential time-dependent deterioration considered in this paper is typical combinatorial optimization problem, and GA, SA and AIS are known as effective and efficient algorithms for combinatorial optimization problems [3, 16, 31].

3.1 Genetic algorithm

Genetic algorithm first introduced by Holland [14] is one of the evolutionary optimization methods that inspired by the laws of evolutionary biology such as inheritance, biology mutation and Darwin's principles of choice. Natural selection is the process through which organisms that are more adapted to their environment are more likely to survive and reproduction and can pass on their genes to the next generation.This algorithm starts with an initial set of solutions (initial population). Each member of the population is called a chromosome that defines a solution to the problem. Chromosomes are evaluated based on the performance criterion and are evolved through continuous repetition. To produce each generation, the new chromosomes are produced by combination (the crossover operator) or alteration (the mutation operator) of the previous generation chromosomes. This process continues until the stopping criterion is met. In the following paragraph, we have briefly explained the steps of the proposed algorithm.

• 1. Arranging the genetic algorithm parameters.

• 2. Producing and evaluating the randomly selected initial population.

• 3. Selecting the individuals and the parents from the population to implement the mutation and crossover operators.

• 4. Combining the actual population, the offspring population and the population of mutated ones to choose the actual population of the new generation.

• 5. Stopping at values of the predetermined repetitions.

In the present study, parents have been selected based on the Roulette wheel selection (fitness proportionate selection). It is one of the operators used in GA. In fitness proportionate selection, as in all selection methods, the fitness function assigns a fitness level to possible solutions or chromosomes. This fitness level is used to assign a probability of selection to each individual chromosome. If $f_{i}$ is the fitness of individual $i$ in the population, its probability of being selected is equal to relation (13).

$$P_{i} = \frac{{f_{i} }}{{\mathop \sum \nolimits_{j = 1}^{N} f_{j} }}$$

(13)

where $N$ is the number of individuals in the population [4]. Moreover, we applied elitism method in which the best chromosomes are moved from the previous stages to the present stage.

3.2 Simulated annealing algorithm

Simulated annealing algorithm (SA) is a kind of neighborhood search-based meta-heuristic algorithm which uses probabilistic and mathematical to find the global optimum. In other words, this algorithm attempts to approximate global optimization in a large space. The name of the aforesaid algorithm comes from annealing process in metallurgy which involves heating and then controlled cooling of a material to increase the size of its crystals. For the first time, this algorithm was introduced by Kirkpatrick et al. [18]. The main advantage of simulated annealing is its ability to avoid getting stuck at the local minimum. This approach not only accepts changes that improve the objective function, but also accepts some changes, with a certain probability, that do not improve the objective function solution in order not to get caught up in a local solution.

As a whole, the following phases were used in the algorithm SA:

• 1. Define the initial configuration set $S$.

• 2. Set the initial temperature $T > 0$.

• 3. If stop criterion invalid,

  • 3.1 Execute the following loop

  • 3.2 Select a random neighborhood from $S$ and call it $S^{{\prime }}$

  • 3.3 Let $\Delta = {\text{cost}}\,S^{{\prime }} - {\text{cost}}\,S$

  • 3.4 If $\Delta \le 0$ then $S^{{\prime }} = S$.

  • 3.5 If $\Delta > 0$ then $S^{{\prime }} = S$ with a probability $e^{{ - \left( {\frac{\Delta }{T}} \right)}}$.

  • 3.6 $T$ as a controlling parameter. It is small, however, close to 1.

• 4. Return to S.

In the simulated annealing algorithm, in addition to the main loop of the algorithm, we defined an internal loop for the algorithm. It is clear that this will only reduce the temperature of the system after the inner ring is completed. Therefore, the search algorithm increases at a constant temperature and the probability of discovering better points increases.

3.3 Artificial immune system algorithm

Like the genetic algorithm, artificial immune system algorithm is inspired by natural behavior in the real world. It was first introduced by De Castro et al. [9]. This algorithm is inspired by the biological immune system in dealing with pathogens. It is similar to the genetic algorithm in many aspects; however, there are differences in the process of the algorithm that enable this algorithm to be faster to converge and to need lower number of calculations. The phases of artificial immune system algorithm are as follows:

• 1. Setting a randomly selected initial population of antibodies.

• 2. Evaluating each antibody by the objective function.

• 3. Selecting the best antibodies to perform reproduction.

• 4. Performing the reproduction for each selected antibody.

• 5. Implementing the mutation operator on the reproduced antibodies based on the level of overlap between them (the objective function).

• 6. Replacing the worst antibodies in the reference population with the best ones in the mutated population.

• 7. Return to 2, until the stop condition is reached.

3.4 Chromosome representation

According to Fig. 1, representation of chromosomes in three algorithms is in form of a special character.

Fig. 1

Chromosome representation with the special character

We have used swap and reversion mutations to implement the mutation operator in genetic algorithm, generate neighborhood solution in the simulated annealing algorithm and mutation on antibodies in artificial immune system algorithm. According to Fig. 2, in the swap mutations, first a chromosome is randomly selected. Then two genes of the chromosome are selected randomly and their places are exchanged to implement the mutation operator. Moreover, according to Fig. 3, in the reversion mutation, first two points of a chromosome are randomly selected and the genes between these two points are reversed.

Fig. 2

Swap mutation

Fig. 3

Reverse mutation

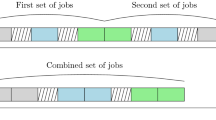
According to Fig. 4, in order to implement the crossover operator in GA of generation A, two chromosomes were randomly selected and the single-point crossover was implemented on them to generate the offspring population. To do this, we first perform the crossover operation and then by keeping the second part of the child's chromosomes constant, delete the repeated genes in the first part and put the values never used in the chromosome in the blank spots.

Fig. 4

One-point crossover

4 Computational results

Based on past and extensive experiences in this field, in this study we adjusted the parameter levels so that the algorithms are optimized at a relatively equal time. Accordingly, we investigated the effective parameters of GA, SA and AIS algorithms using Taguchi method in Minitab software.

The method of designing Taguchi experiments was introduced in 1960 by Professor Taguchi [22]. Taguchi developed a new experimental design method to increase the efficiency of implementation and evaluation of experiments. Its structure is more suitable for evaluating production processes because the required number of experiments is reduced significantly. The design of experiment using the Taguchi method provides a simple, efficient and systematic approach to determine optimum conditions [10]. Taguchi method offers orthogonal arrays as a mathematical tool that analyses the smallest number of experiments that have a large number of parameters. Thus, it would reduce time and effort. In this method, experimental results are converted to a signal/noise (S/N) ratio which means a ratio of an average standard deviation [30]. A larger S/N ratio indicates a better test result. So in experiments, a level of the factor which has the highest ratio represents a better performance. The ratio allows controlling mean and variance while at the same time an analysis of variance (ANOVA) is performed. In this way, the effects of factors can be revealed statistically. S/N ratio can be calculated with Eq. (14):

$$S/N\,{\text{Ratio}} = - 10\,{\text{Log}}_{10} \left[ {\frac{1}{n} \times \mathop \sum \limits_{i = 1}^{n} y^{2} } \right]$$

(14)

n, the number of observations in the experiment and y_i makespan values ($i = 1\,{\text{ton}}$).

The parameter levels are presented in Table 1 for all three algorithms. For the experiments, we considered 100 job and 4 machines with a degradation rate of 0.45. The processing time of the jobs were randomly selected from the intervals [1, 50]. And an average of 30 times run were used for each experiment. To get the exact average of each. According to the number of parameters and levels, for each of the GA, SA and AIS algorithms, 9 different experiments are performed according to the table (orthogonal), i.e. in total, for each of the algorithms, 9 × 30 = 270 separate experiments were performed.

Table 1 Factors and test levels GA, SA and AIS

According to Fig. 5, we considered for GA the initial population of 60, the number of iterations 200, the crossover and mutation rates of 0.75 and 0.25.

Fig. 5

Mean and S/N ratio diagram for GA

According to Fig. 6, we considered for SA the iterations of the main loop 200, the inner loop iterations 50, the initial temperature 30 and the temperature reduction coefficient 0.90.

Fig. 6

Mean and S/N ratio diagram for SA

According to Fig. 7, we considered for AIS the number of iterations is 200, the number of antibodies 20, and the number of antibodies that have the highest compatibility with the antigen 6. We performed the numerical experiments on a computer with Intel core i3, 1.8 GHz and RAM 4 GB. The processing time of the jobs were randomly selected from the intervals [1, 50].

Fig. 7

Mean and S/N ratio diagram for AIS

In this paper, the quality of the answers obtained from the meta-heuristic algorithms has been evaluated by the relative percent deviation (RPD) from the best-known solutions. RPD is a criterion for unsealing data. The reason for using RPD is to normalize the outputs for comparison. A lower RPD RPD value indicates a more optimal answer which is calculated by expression (15).

$${\text{RPD}} = \frac{{{\text{method}}_{{{\text{sol}}}} - {\text{Best}}}}{{{\text{Best}}}} \times 100$$

(15)

where method_sol equals the value of the objective function obtained from the meta-heuristic (GA, SA and AIS) solution and (Best) equals the optimized answer obtained from the model solution by general algebraic modeling system (GAMS) software in the certain form. (GAMS is a high-level modeling system for mathematical optimization and designed for modeling and solving linear, nonlinear, and mixed integer optimization problems. The system is tailored for complex, large-scale modeling applications.) Moreover, in the following tables, $m$ is the number of the machines, $n$ is the number of jobs, and $\alpha$ is the deterioration rate. GA, SA and AIS in Table 3 are twice as large as the best obtained value and mean equals their means in 30 times of RUN in three algorithms. MAD stands for the mean absolute deviation.

Table 2 Test results of small-sized problems

In Table 2, we evaluated the performance of the algorithms (GA, SA and AIS) in small scales ($m = 3;$ $n = 7, 8, 9$ and $m = 4;$ $n = 7, 8$ and according to the study Wang et al. [35] $\alpha = 0.05, 0.45, 0.85$) in comparison with the optimized answer obtained from the optimized solution (GAMS) of the total number of 15 problems for each methods.

The zero RPD index indicates that all three considered meta-heuristic algorithms are efficient for this problem. In Table 3, we evaluated three algorithms of GA, SA and AIS in average scale ($m = 3;$ $n = 30, 40;$ $\alpha = 0.05, 0.45$) and in large scale ($m = 4, 5, 6;$ $n = 100, 150, 200;$ $\alpha = 0.05, 0.45$) performing the algorithm 30 times for each problem and 420 problems for each of the algorithms (GA, SA and AIS).

Table 3 Test results of medium and large-sized problems

Solving the problem in medium and large scales shows that in 30 times running the algorithms according to the best solution obtained, the mean of the answers and the values of MAD, SA are more optimum than GA and AIS. Moreover, as we employed the exponential function of deterioration, we witness some differences in the final answers given the deterioration rate and the size of the problem that MAD values indicate this.

According to Figs. 8, 9 and 10, we see that the convergence speed of the SA is higher. In the following, we interpret the results of three algorithms using Wilcoxon rank-sum test in Minitab software. Mann–Whitney U test or Wilcoxon rank-sum test is a nonparametric test that examines the difference between two independent groups regarding a variable with rank or sequential data [21]. In fact, this test is the nonparametric equivalent of the independent t test, but with the difference that the t test is parametric and its data is continuous, while the Mann -Whitney U test is nonparametric and is performed with rank data. The null and two-sided research hypotheses for the nonparametric test are stated as follows:

• 1. All the observations from both groups are independent of each other,

• 2. The responses are ordinal (i.e., one can at least say, of any two observations, which is the greater),

• 3. Under the null hypothesis H₀, the distributions of both populations are equal [25].

• 4. The alternative hypothesis H₁ is that the distributions are not equal.

Fig. 8

Convergence diagram of GA with $\alpha$ = 0.45, $n = 200$ and $m = 6$

Fig. 9

Convergence diagram of SA with $\alpha$ = 0.45, $n = 200$ and $m = 6$

Fig. 10

Convergence diagram of AIS with $\alpha$ = 0.45, $n = 200$ and $m = 6$

The Mann–Whitney test statistic is defined as Eqs. (16) and (17), [38]:

$$U_{1} = R_{1} - \frac{{n_{1} \left( {n_{1} + 1} \right)}}{2}$$

(16)

$$U_{2} = R_{2} - \frac{{n_{2} \left( {n_{2} + 1} \right)}}{2}$$

(17)

where $n_{1}$ and $n_{2}$ are the sum of groups 1 and 2 and $R_{1}$ and $R_{2}$ are the sum of the ranks of groups 1 and 2, respectively. A smaller value between $U_{1}$ and $U_{2}$ is used for comparison in the test phase. Therefore according to Eq. (18):

$$U = \min \left\{ {U_{1} ,U_{2} } \right\}$$

(18)

If the $U$ statistic at the $1 - \alpha$ confidence level is greater than the value obtained from the table, the null hypothesis is not accepted. In the statistical significance test of $U$, if the smaller group size is 20 items or less and the larger sample size is 40 items or less, the U Mann–Whitney critical value table is used. However, if the volume of both groups is greater than 20 or the volume of one of them is greater than 40, then the distribution of the $U$ statistic tends to the normal distribution. In this case, by calculating the mean and standard deviation, $U$ is calculated and the $Z$ statistic is calculated using Eq. (19).

$$z = \frac{{U - m_{u} }}{{\sigma_{u} }}$$

(19)

where in $m_{u} = \frac{{n_{1} n_{2} }}{2}$ Average $u$ $\sigma_{u} = \sqrt {\frac{{n_{1} n_{2} \left( {n_{1} + n_{2} + 1} \right)}}{12}}$ the standard deviation is $U$. If the value of $Z$ statistic is greater than the value obtained from the standard normal distribution table for the $1 - \alpha$ confidence level, the null hypothesis is not confirmed. Therefore, in this study, we examined the results of SA with GA and AIS in the confidence interval of 0.95.

In the SA, GA test, H₀: The average SA population is lower than GA, and In the SA, AIS test, H₀: The average SA community is less than AIS.

In Table 4, given a significance probability of 0.3826, we cannot reject the null hypothesis. Therefore, SA is less than GA and AIS.

Table 4 Wilcoxon rank-sum test results

In Fig. 11, we see the problem solving time diagram with the three algorithms GA, SA and AIS, which show that in larger sizes the time to solve SA is less than GA and AIS.

Fig. 11

Comparison of the solution time of GA-SA-AIS method

In Fig. 12, we see the most optimal solving values in 30 times the iteration of the solution with the three meta-heuristic algorithms GA, SA and AIS, which shows that the SA method provides more optimal values.

Fig. 12

Comparison of the best answer with 30 times of repetition

In Fig. 13, we see the mean values of the solutions obtained 30 times in the solution of the three meta-heuristic algorithms GA, SA and AIS. Which shows that the SA method provides more optimal values.

Fig. 13

Comparison of mean values with 30 times of repetition

5 Conclusions

In this paper, we considered scheduling problem with exponential time-dependent deterioration in the study of Wang et al. [35] in which they assessed the actual processing time of jobs according to the previous scheduled jobs. They formulated the model and proposed a mixed integer programming formulation for this problem and used two heuristic algorithms which utilize the V-shaped property for the problem of the smallest total completion time and showed that the proposed algorithms provide the optimal solution. Due to the importance of the problem and its implications in different settings, we reached a more effective approach by implementing the aforesaid relation in the setting of identical parallel machines. (Theoretically, the problem of parallel machines can be regarded as the generalization of single-machine problems and a special form of existing scheduling problems in flexible production systems. When it comes to practice, there are also some similar working stations in many production settings that have a lot of similar equipment with similar or different practical characteristics). To solve the problem in small scale, we developed a mixed integer programming model with the objective function $C_{\max }$ that improves the optimized use of the machine and the level of efficiency. In order to solve the problem in larger scales, we applied three meta-heuristic algorithms GA, SA and AIS. Finally, after tuning of parameters GA, SA and AIS using Taguchi method and analyzing the results with Wilcoxon rank-sum test, we showed that by expanding the problem scale and the deterioration rate, SA has a higher efficiency than GA and AIS. Future studies can evaluate the effectiveness of other meta-heuristic algorithms related to this problem. Moreover, they can analyze scheduling problem with exponential deterioration in other scheduling environment that embraces a vast area in scheduling problems.