Abstract
Goncha Siso Eneses area of East Gojam Zone in northwestern Ethiopia is one of the most landslide-prone regions, which is characterized by frequent landslide occurrences causing fatalities and damages in cultivated and non-cultivated lands, infrastructure and properties. Hence, preparing a landslide susceptibility map is very helpful in reducing the damages in infrastructure and properties and loss of animal and human lives. In this study, GIS-based information value and logistic regression models were applied. A reliable and detailed landslide inventory with 894 landslides was prepared through detailed fieldwork and Google Earth image interpretation. These landslides were randomly divided into training data set for model development and testing data set for model validation. Nine landslide causative factors like slope, curvature, aspect, lithology, distance to stream, distance to lineament, distance to spring, rainfall and land use/cover were integrated with training landslides to determine the weight(s) of each landslide factor and factor classes using Information Value and Logistic Regression models, respectively. The landslide susceptibility index map was then produced by summing the weights of all the landslide factors using raster calculator of the spatial analyst tool in GIS. To evaluate the performance of the information value and logistic regression models for landslide susceptibility modeling, the relative landslide density index and area under the curve (AUC) of the receiver operating characteristic curves were performed on both the training and testing landslide data sets. The model has an AUC accuracy of 88.9% success rate and 85.9% prediction rate for information value model whereas 81.8% success rate and 80.2% predictive rate for logistic regression model.
Similar content being viewed by others
1 Introduction
Natural hazards, particularly landslides, are affecting most parts of the world by causing damages in farmlands, engineering structures and loss of human lives [1,2,3,4,5]. These problems commonly occur in mountainous regions where the topography is rugged. These catastrophic natural hazards become an impediment to the development of both developed and developing countries [6]. Landslides in Ethiopia have resulted in a loss of human and animal lives, damages in infrastructures and properties in the last 5 decades. From 1960 to 2010 alone, 388 people died, 24 people injured, a wide area of cultivated and non-cultivated land, environment, infrastructure, and houses were affected [7,8,9,10]. In 2018, rainfall triggered landslides also caused the death of 62 people, injury of 30 people, displacement of 5091 households, damage of houses and destruction of both cultivated and non-cultivated land in different parts of the country. Although the landslide problem is critical in Ethiopia, still there is no adequate landslide susceptibility mapping in the different parts of the country. Goncha Siso Eneses is one of the areas that was recently affected by the landslide incidences and so far the area was not yet studied. Landslide in this area resulted in the damage of houses, gravel roads, farmlands and loss of animal and human lives. From local people’s witness, deep-seated rotational landslides occurred in 2014 and were reactivated in 2018 in Gete Semane village which caused the destruction of one house in 2014 but in 2018 landslide in the study area destroyed one house, cracked the floor of four houses, displaced people from seventeen villages and damaged 44-ha farmlands that were covered by maize, almond, buckthorn and fruits. Generally, the landslide incidences in the study area caused damages in bridges, houses, farmlands with crops, fruits & eucalyptus trees and also caused few fatalities. In 2018 alone, landslides caused the damage of 233.1 ha of farmland, death of eight people and destruction of five houses.
To identify the landslide-prone areas, researchers in different parts of the world have implemented various approaches and techniques. References [11,12,13,14] applied knowledge-based approaches. References [2, 15,16,18] used statistical approaches. Deterministic approach was applied by Gorsevski et al. [19], while a combination of deterministic and statistical modeling approaches was applied by Yilmaz and Keskin [20]. These techniques of landslide susceptibility mapping can be classified into qualitative and quantitative methods. The qualitative method is an expert-based technique that has subjectivity problem during rating of weights for conditioning factors [21,22,23,24,25]. This relies on human judgment, but the quantitative method uses mathematical expressions in slope stability analysis rather than descriptive ones [26]. Among the quantitative methods, statistical methods are the most popular and highly applied techniques in landslide susceptibility modeling. Statistical approaches are important to determine the spatial distribution of landslide and its relationship with different landslide causative factors. These methods are preferred in areas where geotechnical data are scarce and the area is relatively large. However, these methods do not provide the factor of safety that provides quantitative information about slope instability [27]. Information value and logistic regression models are most commonly applied for landslide susceptibility mapping with a good degree of reliability [28]. Geotechnical approaches provide a numerical value that explains the intrinsic condition of the slope material unlike statistical approaches. However, the geotechnical approach is expensive and time-consuming. The main objective of this study is to prepare a landslide susceptibility map of Goncha Siso Eneses area using information value and logistic regression models.
1.1 Study area
Goncha Siso Eneses area is located in Northwestern Ethiopia, which is characterized by mountain peaks, deep gorge (valley), plateau and undulating topography with minimum and maximum altitudes of 1198 m and 3199 m, respectively (Fig. 1). The area is bounded between 37.9°E and 38.39°E longitude and 10.8°N and 11.06°N latitude. Goncha Siso Eneses area is also characterized by tropical (1830 m), subtropical (1830–2440 m) and cool (> 2,440 m) climate zones. Annual rainfall of the study area varies from 762 to 1824 mm. The annual rainfall distribution showed a pronounced seasonality with the heaviest rainfall being in July and August. The mean temperature of the area is 18.5 °C with a mean minimum and maximum daily temperature of 11.4 °C and 25.5 °C, respectively [29].
2 Materials and methods
For this research, field survey, Google Earth image analysis, GIS-based information value and logistic regression models were applied. Moreover, relevant data like topographic maps, DEM (30 m × 30 m resolution), geological reports and maps, meteorological data and borehole data have been collected. These data were collected from Ethiopian Mapping Agency, United States Geological Survey (USGS), Geological Survey of Ethiopia (GSE), Ethiopian National Meteorological Agency, Amhara Water Well Drilling Enterprise (AWWDE), field survey and Google Earth image.
The landslide inventory map was prepared using extensive field survey and Google Earth image interpretation. This was randomly divided into training and testing landslide data sets (Fig. 3). The testing landslide dataset is used to verify the accuracy of landslide susceptibility maps. Using ArcMap 10.1, conditioning and triggering factor maps were prepared. Slope, aspect, curvature and streams have been extracted from 30-m-resolution DEM. The geology of the study area including the lithology and geological structures (mainly lineaments) was collected from field survey in order to update the existing lithology and structural (lineament) maps. During the field work, locations of springs were also collected. Buffering analysis was done to obtain the distance to lineament, distance to springs and distance to stream parameters. The land use map was digitized from Google Earth image as it was possible to get a more reliable result due to its high spatial resolution and easiness in terms of its manual classification. Generally, the general flowchart that showed the procedures to be followed in this research work is summarized in Fig. 2. The rainfall raster map was prepared by interpolating the 30-year rainfall data of twelve rain gauge stations near to the study area using the IDW spatial analyst tool to get an interpolated and spatially distributed rainfall raster map.
In landslide susceptibility mapping, building a database is the most important task. Therefore, two databases were built for the information value and logistic regression models. The information value database contains landslide inventory and landslide factors, while the logistic regression database contains landslide and non-landslide points with nine landslide factors information values. After the calculation of information values, the information raster maps were prepared in ArcGIS. Then, these maps were summed using the raster calculator in ArcGIS to get the landslide susceptibility index (LSI). In the case of logistic regression model, the study area was classified as training landslide and non-landslide points using a random point in fishnet. Then, the information values of the nine factor maps were extracted in order to generate logistic regression coefficients of each landslide factor in SPSS, and finally, the landslide susceptibility index of the area was generated using the logistic regression probability equation in GIS.
The landslide susceptibility index maps in both methods were further reclassified using the reclassify option of the spatial analyst tool in order to get the predicted landslide susceptibility maps. In logistic regression model, the LSI map was extracted with training and testing landslides data which are used to judge the performance of the model using ROC, landside density and relative landslide index (R-index). Finally, the landslide susceptibility index maps were classified into very low, low, moderate, high and very high landslide susceptibility classes using the natural breaks method.
2.1 Landslide inventory
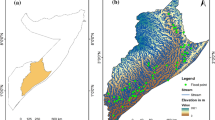
In landslide susceptibility mapping, landslide inventory is the most important component of slope stability analysis. In the present work, 894 landslides, which covered an area of 49.8 km2 (Fig. 3), were identified from old scarps and active slides using detailed field survey and Google Earth image interpretation. The landslide inventory was randomly classified into training (699 landslides) and testing (195 landslides) datasets by considering their spatial distribution into account. Landslide types in the study area include rockslide, soil slide, debris flow, earth flow, rock fall and rock toppling. From Google Earth time-series image interpretations, the study area has been affected by landslide incidences since 2006.
2.2 Landslide factors
For the selection of landslide factors, there are no well-known standard criteria until now. However, nine landslide factors including lithology, land use/land cover, slope, aspect, curvature, distance to springs, distance to stream, distance to lineament and rainfall were used in this study. These landslide factor maps were prepared and classified into subclasses (Table 1, Fig. 4a–i) to determine the contribution of each factor class for landslide occurrence. Slope, aspect, curvature and distance to stream maps were derived from ASTM 30-m-resolution DEM (Fig. 4 a, b, e and c) and classified into different classes (Table 1). Lithology map (Fig. 4d) was updated based on field survey and the distance to lineament map (Fig. 4f) was prepared using buffering analysis. Land use/cover map (Fig. 4i) was digitized from Google Earth image interpretation, which can be exported to GIS layer format and verified in the field for the final map. Based on spring location data from extensive field work, distance to spring map was generated (Fig. 4g). Rainfall map (Fig. 4h) was prepared by interpolating the 30-year rainfall data of twelve rain gauge stations which are found within and near to the study area using IDW interpolation technique of the spatial analyst tool in GIS. The details of all the landslide factors and their weights of IV with respect to landslide occurrence are summarized in Table 1.
2.3 Information value model
The information value model is a bivariate statistical method which is used to predict the spatial relationship between landslides and landslide factor classes [30]. This method was developed by Yin and Yan [31] and modified by Sarkar et al. [32]. In the present work, the information values have been determined for each class of a factor map based on the presence of landslide in a given map unit. The calculated information value helps to determine the role of each factor class for landslide occurrence [33]. All factor maps were converted into raster maps with the same coordinate system (Adindan UTM zone 37 N) and the same pixel size (30m × 30m) and were reclassified into different classes. The landslide inventory map was randomly divided into training landslides (78%) and testing landslides (22%) by considering their spatial distribution into account. The rasterized training landslide map was overlaid over the rasterized landslide factor maps using ArcGIS software to calculate the information values for all classes of each factor map using the information value model. The information value of a certain factor class was calculated using the log value of the ratio of conditional probability to prior probability. The conditional probability was calculated by dividing the landslide pixels in a single factor class to pixels of a subclass of landslide factor, while the prior probability was calculated by dividing the total landslide pixels in the study area to the total pixels in the entire study area using Eq. (1) as follows.
where Nslpix is a number of landslide pixels in a given class, Ncpix is the number of pixels in a given class, Ntspix is a total number of landslide pixels in the study area, and Ntapix is a total number of pixels in the entire study area. The weights of all factor classes were calculated through the ratio of landslide density of each factor class to the landslide density of total area, or the information value can provide the landslide probability in each class and in the total area (Table 1). If IV > 0.1, the factor classes will have the highest probability of landslide occurrence, but factor classes with negative values indicate the presence of a factor with no significant contribution to landslide occurrence.
2.4 Logistic regression model
Logistic regression is one of the popular multivariate statistical analysis models which can be used to establish a multivariate regression relationship between dependent and independent variables [34]. Among other statistical methods, logistic regression model has been proven one of the most reliable approaches for landslide susceptibility mapping and determining the most landslide influencing factors [16, 28, 35,36,37,38,39]. This model is advantageous as it does not require normal distribution and it uses continuous or discrete variables. The difficulty of using the logistic regression model lies on sample size selection of dependent and independent variables for landslide susceptibility analysis. There are three ways of sampling landslide and non-landslide points [40]. The first way is using all data from all the study areas. However, this leads to an uneven proportion of non-landslide and landslide pixels which incorporate a large volume of data in the analysis [41, 42]. Using all landslide pixels with equal non-landslide pixels is the second method which also results in a less reliable output, but it can reduce sample size and sampling bias. The third method uses an unequal proportion of landslide and non-landslide pixels [1, 43]. In the present work, the landslides of the study area were classified into training landslides (78% with 699 landslides) and as testing landslides (22% with 194 landslides). This method requires SPSS or R software to calculate the coefficient of each factor map. It can be expressed mathematically [37, 44] as:
where P is the probability of landslide occurrence that varies from zero to one. Z is the linear combination of the predictors and varies from − 1 < z < 0 for higher odds of non-landslide occurrence to 0 < z < 1 for odds of higher landslide occurrence. Z can be defined as:
where \(x_{1} , \, x_{2} , \, x_{3} \ldots x_{n}\) are independent variables, Bo is the intercept of the slope of logistic regression analysis, and \(\beta_{1} , \, \beta_{2} , \, \beta_{3} \ldots \beta_{n}\) are the coefficients of the logistic regression analysis.
3 Result and discussion
3.1 Information values (IV) model
The landslide inventory map was overlaid with the factor maps to determine the significance of each factor class for landslide occurrence. Using information value equation, the information value for each factor class was calculated and the factor classes which have positive information values of > 0.1 will have the higher probability of landslide occurrence (Table 1).
The IV results in Table 1 indicates that the slope of the study area will have a significant influence to landslide occurrence, especially on slope classes of 20°–27°, 27°–32°, 32°–39°, 39°–48° and 48°–74°. This is because the material covering these slope classes is loose unconsolidated sediment at a shallow depth, which will slide when it is subjected to heavy and prolonged rainfall and a change in slope geometry. However, the IV values for gentle and very gentle slope classes are negative which implies no effect on slope instability. Landslides occurred more frequently on steep slopes than on gentle slopes. However, landslides can also occur in gentle slopes when other landslide factors like slope modification (excavation and mining), active gully and riverbank erosion/scouring are undertaking. Field observations showed that landslide can occur in gentle slopes but may not form a long run out distance due to its moderate slope gradient. The IV of aspect class in Table 1 showed that the aspect classes of flat, N and SW facing slopes have significant landslide occurrences which include 9%, 10%, 11% and 11% of the total landslides in the study area as streams and springs are concentrated in these aspect classes. However, other aspect classes that covered 59% of the study area have no slope instability/landslide problem.
Lithology is one of the most influencing factors that cause slope instability problems depending on the inherent properties of rocks and soils. From the information value results in Table 1, the slightly weathered basalt and colluvial soil deposits showed high IV values that will have a high probability of landslide occurrence. The slightly weathered basalt developed thin layers of soils, which have a significant effect on slope instability in the area resulting from the fast rate of saturation. In general, as the depth of the soil mass decreases, it will saturate within a short period. This increases the probability of slope instability in such thin soil masses. Colluvial soil deposit, which contains unconsolidated recent soil deposit, is another problematic slope mass in the study area that causes slope instability problem due to its loose nature and its dispersion ability when it gains water. Land use/cover is one of the most decisive factors for slope instability problems, but the study area is not exposed to huge anthropogenic activities like construction of big infrastructures and engineering structures. Agricultural activity is the most commonly and intensively practiced activity in the flush portion of the streams. As a result, the IV value for agricultural activity is negative which means agricultural activities have no effect on slope instability. Nevertheless, if the agricultural activity is practiced in the sheer slope portion, it might have a pronounced effect on slope instability. Among the land use classes, the water body has the highest IV values indicating that it will have the highest influence or effect on landslide occurrence. It is known that water is one of the key elements that controls slope stability. This is because water can cause gully and riverbank erosion, can add weight on a slope due to saturation of the soil, can lubricate fracture and cracks of rocks and soil mass and can decrease the shear strength of the soil mass by increasing pore water pressure when the pore space in soil mass is filled with water. The IV value for moderately forested region is nearer to 0.1, indicating that the presence of forest on the slope is important in slope stabilization when the trees are planted on the slope toe and when the tree roots crossed the potential failure surface. The effects of vegetation on slope stability can be grouped into hydrological and mechanical effects. The hydrological effect can reduce soil moisture by removing water from the slope through evapotranspiration and uptake of water with its roots. This can lessen pore water pressure in a soil mass, whereas the mechanical effects of vegetation are associated with the anchorage of failure planes through their roots when the roots cross the failure surface in the soil mass. Landslides did not occur in forested parts of the study area due to the root anchorage by vegetation and reduction of the moisture content through evapotranspiration process. This makes the vegetated areas to be less susceptible to slope instability problem. In most cases, bare land has a great role in slope instability by facilitating other factors like soil erosion. The IV value for the bare land use type in the study area showed high values which can make the slope unstable. But this may not always be true as it is highly dependent on the properties of slope material. Grazing land is another land use type which has a great role on landslide occurrence as it increases the rate of soil and gully soil erosion, thereby making the slope to be unstable. The IV value for the distance to spring class in between 0 and 812 m is high, indicating the high probability of landslide occurrence. This shows that the landslides are more frequent in the close vicinity of springs.
Mostly, landslides occurred closer to the river/stream courses because of stream/riverbank erosion. This is common in the study area. As the IV values in Table 1 indicated, distance to stream (0–100 m) which is closer to the river/stream showed higher IV value with a significant effect on landslide occurrence. About 36.14% of the landslide areas are found in this factor class.
The slope instability problem is also associated with slope gradient, slope aspect and slope curvature. As the information value results in Table 1 indicated, the slope curvature has great contribution to landslide occurrence in the study area. The slope curvature can be classified into flat, concave and convex shapes. The concaveness of the slope has a significant impact on landslide occurrence in Inegode and Angot villages which covered 33% of the total landslides. When the slope shape is bowl-shaped, it is favorable for water impoundment. The impounding water infiltrated into the ground and developed pore water pressure that can reduce the effective stress of the soil. About 5% of the landslide areas are found in convex slopes which promote landsliding due to the effect of gravity.
3.2 Landslide susceptibility index (LSI)
After information values are assigned for each factor class, landslide susceptibility index map of the study area was prepared by summing all the information value raster maps using a raster calculator in the spatial analyst tool of ArcGIS as shown in Eq. (4). The landslide susceptibility index map requires further reclassification. For this purpose, various classification techniques are available like natural breaks, standard deviation, equal interval, manual and quantile techniques in GIS. However, the classification techniques to be applied depend on the type and distribution of data. The natural breaks method is important for unevenly distributed data, and it is capable of classifying the landslide susceptibility index map into different categories based on the inherent data value similarity [17, 45]. In the present work, the final landslide susceptibility index map of the study area was classified into five classes of very low, low, moderate, high and very high susceptibility using the natural breaks as indicated in Figs. 5 and 6. The high and very high landslide susceptibility classes covered 36% and 20% of the study area for the information value and logistic regression models, respectively. These classes mostly fall in a steep slope, concave-shaped slopes, river gorge and active gully soil erosion areas. The very low and low landslide susceptibility classes are found in low land and in plateau areas. The moderate susceptibility classes are concentrated along small streams. The result of landslide susceptibility map from information value model in Table 2 revealed that 23% and 13.3% of the area fall under high and very high landslide susceptibility classes, but the remaining 11.4%, 22.8% and 29.5% of the area fall under very low, low and moderate susceptibility classes, respectively.
In the case of logistic regression model, 12.6% and 7.1% of the area fall under the high and very susceptibility classes but the rest classes that comprise 28.6%, 30.8% and 20.9% of the area fall under very low, low and moderate susceptibility classes, respectively (Table 3). Using SPSS software, the intercept values and coefficients of all the factor maps were determined and an equation constituting these coefficients and intercept value were established as can be seen in Eq. (5) and Table 4 and the final landslide susceptibility map from logistic regression was obtained using Eq. (6).
3.3 Model validation
Landslide susceptibility map without validation will not give meaning in the scientific sense. For this purpose, various validation techniques were applied. In the case of model validation, the landslide area has been classified based on time, space and random partition [16, 17, 46]. In the present work, the landslide area was randomly classified into 78% landslides for training and 22% landslides for model validation by keeping their spatial distribution into account using the random partitioning technique [17, 46]. The landslide susceptibility model for the study area was developed using the training dataset. The models were validated by applying various validation techniques like simple overlay, relative landslide density index (R-index) and receiver operating characteristics (ROC) curve (Figs. 7 and 8).
3.3.1 Overlay method
From the overlay of training and validation landslide data sets over the landslide susceptibility map, the percent and density of training and validation landslides were calculated which increases from very low to very high landslide susceptibility classes. This again confirmed that the model is reliable and accurate (Table 5 and Fig. 7). The higher the number of landslide pixels in the high and very high landslide susceptibility index, the higher will be the model accuracy [17].
3.3.2 Relative landslide density index (R-Index)
The landslide susceptibility models in this study were also validated using a relative landslide density index which is calculated using the following equation.
where ni is the number of landslide in a landslide susceptibility classes, while Ni is the number of landslide susceptibility class pixel within that class. The relative density can be calculated using Eq. (7) through a comparison of landslide susceptibility map with landslide inventory data [47, 48]. The fact that R-index value increases from very low to very high landslide susceptibility classes (Table 5 and Fig. 7a) confirms that the model is accurate and reliable [47, 48].
3.3.3 Receiver operating characteristics (ROC) curve
The area under the receiver operating characteristics (ROC) curve was considered in evaluating the success and predictive rates of both training and testing data sets for information value and logistic regression models using real statistics in Microsoft Excel. The area under the curve (AUC) value ranges from 0.5 to 1 [49]. When the AUC value is in between 0.9 and 1, the model will have excellent performance; if AUC value is in between 0.8 and 0.9, the model will have very good performance. If the AUC value is in between 0.7 and 0.8, the model will have good performance. If AUC value is between 0.6 and 0.7, the model will have average performance. However, if AUC value is between 0.5 and 0.6, the model will have fair performance, but if AUC value is equal to or less than 0.5, then the model will have poor performance. Based on the above explanation, the AUC values in the present models for both success and predictive rates lie in the range of 0.8 and 0.9 showing a very good performance (Fig. 8 and Table 6). Therefore, based on the result of AUC value in the ROC curve, both models that have developed using logistic regression and information value methods are reliable and accurate.
3.3.4 Model comparison
Among different GIS-based statistical models, information value and logistic regression are the most commonly used models for landslide susceptibility mapping. Besides their merits, these models have also limitations. The information value method cannot determine the relationship between landslide factors and landslide, but it helps to know the effects of each factor class on landslide occurrence. As shown in Table 1, the probability of each factor class to cause a landslide incidence can be predicted, but it cannot distinguish which landslide factor is controlling more in the case of information value model. However, this limitation can be solved using logistic regression model which determines the significance of each landslide factor by calculating the logistic regression coefficients of each landslide factor. Nevertheless, this model has also limitations of generalization and simplification of landslide factors. According to [50, 51], the information value method provided a more realistic landslide susceptibility map with a high prediction accuracy than the logistic regression one. However, Bui et al. [51] reported that the accuracy of the two models showed almost an equal predicting capacity, with prediction rates of 94.2% and 95%, respectively. As stated by Zhang et al. [40], the logistic regression model is better than the information value model in landslide susceptibility mapping based on the success and predictive rate curves. However, in the present study, the success rate curve value is 88.6% and the predictive rate curve value is 85.9% for the information value model which is better than the success rate curve value of 81.8% and the predictive rate curve value of 80.2% for logistic regression model. Therefore, the information value model has a better performance than the logistic regression model in predicting the probability of landslide occurrence. This is because logistic regression model has oversimplified the statistical significance of landslide factors. In the present study, landslide factors were classified into different classes and the information value for each factor class was determined. Based on the results of information value, not all factor classes have a significant effect on landslide occurrence. Nevertheless, some of the factor classes in a single factor have a greater effect on landslide occurrence as shown in Table 1. Accordingly, the negative information values have less or no significance on landslide occurrence, while the positive information values that are greater than 0.1 have greater roles in landslide occurrence.
4 Conclusion
In the present work, information value and logistic regression models were applied to prepare the landslide susceptibility maps of the study area. From information value model, the weights of each landslide factor classes were calculated while in logistic regression model, the logistic regression coefficients for all landslide factors were determined. Using logistic regression analysis, coefficients of all the landslide factors with statistical significance to landslide occurrence include slope, land use/cover, lithology, aspect and distance to lineament. But the rest landslide factors like rainfall, curvature, distance to stream and springs with negative coefficients implied that these factors have less significance for landslide occurrence, while the information value of each factor class shows about the contribution of each factor class on landslide occurrence when its value is greater than 0.1.
Based on information value analysis, the factor classes with IV greater than 0.1 include slope (20°–74°), land use (bare land, grazing land and water body), lithology (colluvial soil and slightly weathered basalt), distance to stream (0–100 m), distance to lineament (0–311 m), distance to spring (0–812 m), curvature (concave and convex), aspect (flat, north and southwest) and rainfall (640–785 mm, 785–930 mm).
From the information value and logistic regression raster maps of all the landslide factors, the landslide susceptibility index maps were prepared using a raster calculator of the spatial analyst tool in GIS. These maps were further reclassified in GIS using natural breaks classification method into very low, low, moderate, high and very high landslide susceptibility classes. The road section from Debre Birhan–Tora Meda to Debre Yakob, Tora Meda to Inegode village and new road from Arib Gebeya to Angot village fall under moderate, high and very high landslide susceptibility classes because of intense and active gully erosion, presence of spring, concaveness and convexness of the slope in the area.
The accuracy of the final landslide susceptibility model was tested using the receiver operating characteristics (ROC) curve, simple overlay and the relative landslide density index (R-index) methods by comparing landslide raster with the landslide susceptibility map. From the success and predictive rates of the receiver operating characteristics (ROC) curves, the area under the curve has been determined for each model. Since the value of the area under the curve is close to one, the landslide susceptibility models of the present study have shown acceptable accuracy. Based on the AUC values, the information value model is better than the logistic regression model.
The resulting maps have provided the spatial distribution of landslide occurrences, but these cannot forecast the time, degree of landslide occurrences and how often it can occur [52]. However, these maps can be used by decision-makers, civil engineers or geologists for regional land use and urban planning and for landslide prevention and mitigation. Therefore, the government bodies at the Federal, Regional, Zonal and District levels should take concrete actions to mitigate the problem by afforestation of barren lands, constructing check dams, gabion and retaining walls, relocation of people from unstable slopes and a combination of these remedial measures.
References
Dai FC, Lee CF (2002) Landslide characteristics and slope instability modeling using GIS, Lantau Island, Hong Kong. Geomorphology 42:213–228
Girma F, Raghuvanshi TK, Ayanew T, Hailemariam T (2015) Landslide hazard zonation in Ada Berga District, Central Ethiopia, a GIS-based statistical approach. J Geomat 9:1–14
Kanungo DP, Arora MK, Sarkar S, Gupta RP (2006) A comparative study of conventional, ANN black box, fuzzy and combined neural and fuzzy weighting procedures for landslide susceptibility zonation in Darjeeling Himalayas. Eng Geol 85:347–366
Pan X, Nakumura T, Nozaki Huang X (2008) A GIS-based landslide hazard assessment by multivariant analysis. Landslide J Jpn Landslide Soc 45:187–195
Varnes DJ (1996) Landslide types and processes. In: Turner AK, Schuster RL (eds) Landslides: investigation and mitigation, transportation research board. Special Report 247, National Research Council National Academy Press, Washington, DC
Centre for Research on the Epidemiology of Disasters (CRED) (1998) Economic losses, poverty & disasters. United Nation Office for Disaster Reduction, Geneva
Ayalew L (1999) The effects of the seasonal rainfall on a landslide in the highland of Ethiopia. Bull Eng Geol Environ 58:9–19
Ibrahim J (2011) Landslide assessment and hazard zonation in Mersa and Wurgessa, North Wollo, Ethiopia. Unpublished Master Thesis, School of Graduate Studies, Addis Ababa University, Addis Ababa, Ethiopia, pp 1–10
Woldearegay K (2008) Characteristics of a large-scale landslide triggered by heavy rainfall in Tarmaber area, central highlands of Ethiopia. In: Geophysical Research Abstracts, vol 10
Temesgen B, Mohammed U, Korme T (2001) Natural hazard assessment using GIS and remote sensing methods, with particular reference to the Landslides in the Wondogenet Area, Ethiopia. Phys Chem Earth Part C: Solar Terr Planet Sci (C) 26:615–665
Anbalagan R (1992) Landslide hazard evaluation and zonation mapping in mountainous terrain. Eng Geol 32:269–277
Mulatu E, Raghuvanshi TK, Abebe B (2009) Landslide hazard zonation around Gilgel Bibe II hydroelectric project, Southwestern Ethiopia. SINET: Ethiop J Sci 32(1):9–20
Raghuvanshi TK, Ibrahim J, Ayalew D (2015) Slope stability susceptibility evaluation parameter (SSEP) rating scheme: an approach for landslide hazard zonation. J Afr Earth Sci 99:595–612
Ruff M, Czurda K (2008) Landslide susceptibility analysis with a heuristic approach in the Eastern Alps (Vorarlberg, Austria). Geomorphology 94:3–4
Hamza T, Raghuvanshi TK (2015) GIS-based landslide hazard evaluation and zonation in Jeldu district in central Ethiopia. J King Saud Univ Sci 29:151–165
Lee S, Pradhan B (2007) Landslide hazard mapping at Selangor, Malaysia using frequency ratio and logistic regression models. Landslides 4:33–41
Meten M, Bhandary NP, Yatabe R (2015) GIS-based frequency ratio and logistic regression modeling for landslide susceptibility mapping of Debre Sina area in central Ethiopia. J Mt Sci 12(6):1355–1372
Chandak PG, Sayyed SS, Kulkarni YU, Devtale MK (2016) Landslide hazard zonation mapping using information value method near Parphi village in Garhwal Himalaya. Ljemas 4:228–236
Gorsevski PV, Jankowski P, Gessler PE (2006) A heuristic approach for mapping landslide hazard by integrating fuzzy logic with the analytic hierarchy process. Control Cybern 35(1):121–146
Yilmaz I, Keskin I (2009) GIS-based statistical and physical approaches to landslide susceptibility mapping (Sebinkarahisar, Turkey). Bull Eng Geol Environ 68(4):459–471
Pradhan B (2010) Remote sensing and GIS-based landslide hazard analysis and cross-validation using a multivariate logistic regression model on three test areas in Malaysia. Adv Space Res 45:1244–1256
Pradhan B, Chaudhari A, Adinarayana J, Buchroithner MF (2012) Soil erosion assessment and its correlation with landslide events using remote sensing data and GIS: a case study at Penang Island, Malaysia. Environ Monit Assess 184(2):715–727
Sarkar S, Anbalagan R (2008) Landslide hazard zonation mapping and comparative analysis of hazard zonation maps. J Mt Sci 5:232–240
Sarkar S, Kanungo DP, Patra AK, Kumar P (2008) GIS-based spatial data analysis for landslide susceptibility mapping. J Mt Sci 5:52–62
Wang M, Qiao J et al (2010) GIS-based earthquake-triggered landslide hazard zoning using contributing weight model. J Mt Sci 7:339–352
Landslide Working Party (2011) Guidelines for landslide susceptibility, hazard, and risk assessment, and zoning, pp 1–173
Dou J, Bui DT, Yunus AP, Jia K, Song X, Revhaug I, Xia H, Zhu Z (2015) Optimization of causative factors for landslide susceptibility evaluation using remote sensing and GIS data in parts of Niigata, Japan. PLoS ONE 10(7):e0133262
Ayalew L, Yamagishi H (2005) The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 65:15–31
Teferi E (2015) Soil hydrological impacts and climatic controls of land use and land cover changes in upper Blue Nile basin, Netherland. CRC Press, Boca Raton, pp 22–263
Sarkar S, Kanungo D, Ptra A, Kumar P (2006) Disaster mitigation of debris flow, slope failure, and landslides. GIS-based landslide susceptibility case study in Indian Himalaya. Universal Academy Press, Tokyo, pp 617–624
Yin KJ, Yan TZ (1988) Statistical prediction model for slope instability of metamorphosed rocks. In: Proceedings of the fifth international symposium on landslides, Lausanne, Switzerland, vol 2, pp 1269–1272
Sarkar S, Rjan Martha T, Roy A (2013) Landslide susceptibility assessment using information value method in parts of the Darjeeling Himalayas. Geol Soc India 82:351–362
Kanungo DP, Arora MK, Sarkar S, Gupta RP (2009) Landslide susceptibility zonation mapping a review. J South Asia Disaster Stud 2:81–105
Pradhan B, Lee S (2010) Landslide susceptibility assessment and factor effect analysis: backpropagation artificial neural networks and their comparison with frequency ratio and bivariate logistic regression modeling. Environ Model Softw 25:747–759
Chau KT, Chan JE (2005) The regional bias of landslide data in generating susceptibility maps using logistic regression: case of Hong Kong Island. Landslide 2:280–290
Chen Z, Wang J (2007) Landslide hazard mapping using a logistic regression model in Mackenzie Valley, Canada. Nat. Hazards 42:75–89
Lee S, Sambath T (2006) Landslide susceptibility mapping in the Damrei Romel area, Cambodia using frequency ratio and logistic regression models. Environ Geol 50:847–855
Rickli C, Graf F (2009) Effects of forests on shallow landslides—case studies in Switzerland. For Snow Landsc Res 82:33–44
Sujatha ER, Rajamanickam GV, Kumaravel P (2012) Landslide susceptibility analysis using probabilistic certainty factor approach: a case study on Tevankarai stream watershed, India. J Earth Syst Sci 121:1337–1350
Zhang YS, Igbol J, Yae Y (2017) Landslide susceptibility mapping using an integrated model of information value and logistic regression methods in the Bailongjiang watershed, Gansu Province, China. J Mt Sci 14:249–268
Guzzetti F, Carrara A, Cardinal M, Reichenbach P (1999) Landslide hazard evaluation: a review of current techniques and their application in a multi-scale study, central Italy. Geomorphology 31(1–4):181–216
Ohlmacher GC, Davis JC (2003) Using multiple logistic regression and GIS technology to predict landslide hazard in northeast Kansas, USA. Eng Geol 69:331–343
Atkinson PM, Massari R (1998) Generalized linear modeling of landslide susceptibility in the Central Apennines. Comput Geosci 4:373–385
Schicker R, Moon V (2012) Comparison of bivariate and multivariate statistical approaches in landslide susceptibility mapping at a regional scale. Geomorphology 161–162:40–57
Kouhpeimaa S, Feizniab H, Ahmadib Moghadamniab AR (2017) Landslide susceptibility mapping using logistic regression analysis in Latyan catchment. Desert 22:85–95
Chung CJF, Fabbri AG (2003) Validation of spatial prediction models for landslide hazard mapping. Nat Hazards 30(3):451–472
Raj Meena S, Ghorbanzadeh O, Blaschke T (2019) A comparative study of statistics-based landslide susceptibility models: a case study of the region affected by the Gorkha Earthquake in Nepal. SPRS Int J Geo-Inf 8:94
Shahabi H, Ahmad BB, Khezri S (2013) Evaluation and comparison of bivariate and multivariate statistical methods for landslide susceptibility mapping (case study: Zab basin). Arab J Geosci 6:3885–3907
Yesilnacar E, Topal T (2005) Landslide susceptibility mapping: a comparison of logistic regression and neural networks method in a medium scale study, Hendek region (Turkey). Eng Geol 79:251–266
Yalcin A, Reis S, Aydinoglu A et al (2011) A GIS-based comparative study of frequency ratio, analytical hierarchy process, bivariate statistics and logistic regression methods for landslide susceptibility mapping in Trabzon, NE Turkey. CATENA 85:274–287
Bui DT, Lofman O, Revhaug I et al (2011) Landslide susceptibility analysis in the Hoa Binh province of Vietnam using the statistical index and logistic regression. Nat Hazards 59(3):1413–1444
Das G, Lepcha K (2019) Application of logistic regression (LR) and frequency ratio (FR) models for landslide susceptibility mapping in Relli Khola river basin of Darjeeling Himalaya. India. SN Appl Sci 1:1453. https://doi.org/10.1007/s42452-019-1499-8
Acknowledgements
First, I would like to thank the almighty God who allowed me to accomplish this research work. Next, I would like to give my gratitude to Dr. Kifle Woldearegay, Mr. Tilahun Mersha, Mr. Leulalem Shano (Ph.D. candidate at AASTU), Mr. Zerihun Dawit, Dr. Veera Narayana and Dr. Muralitharan Jothimani for their valuable support and advice during this research work. I would like to give my special thanks to my friends and families for their continuous support during the research work. Finally, I would like to thank Addis Ababa Science and Technology University, University of Gondar, for their finance funding and geological equipment; National Metrological Agency staffs, Geological Survey of Ethiopia, Goncha Siso Eneses wereda Administrative head office, disaster head office, natural resource management head office and the rural community, for their valuable data and continuous support during fieldwork, respectively.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest with professionals or any organization.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Wubalem, A., Meten, M. Landslide susceptibility mapping using information value and logistic regression models in Goncha Siso Eneses area, northwestern Ethiopia. SN Appl. Sci. 2, 807 (2020). https://doi.org/10.1007/s42452-020-2563-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s42452-020-2563-0