Extraction of uncertain parameters of double-diode model of a photovoltaic panel using Ant Lion Optimization

Abstract

This article addresses the problem of estimating the uncertain parameters of solar photovoltaic models using Ant Lion Optimization. The parameter extraction phase consists of three stages, the first stage is devoted to estimating the parameters without considering the uncertainties, the second stage deals with estimating the uncertainties of each parameter, with the aim of reducing of search interval for parameters to extract. Finally, the parameters are extracted instantaneously taking into account the results of the first two steps. For validation of proposed theoretical developments, the algorithm is applied to the academic example of the real data of silicon solar cell RTC France. The results obtained are compared with well-established algorithms. These comparisons have shown that the proposed method presents largely effective performances compared to existing methods in the literature.

1 Introduction

In recent decades, global environmental concerns have increased due to pollution, climate change and global warming have increased. The use of renewable energy sources such as wind, sun, biomass, etc. receives increasing interest. Solar energy is considered one of the most used renewable energy sources in the world because it is high availability and cleanliness. Solar energy is applied in the production of photovoltaic (PV) and thermal energy. For the creation of electricity, solar photovoltaic systems are widely used around the world. However, the use of photovoltaic systems depends on meteorological and environmental factors, such as variations in temperature and overall irradiance. Therefore, there is a need for optimization of the photovoltaic system. This can be achieved by using a precise analytical model based on the measurement data of [current (I), voltage (V)]. In the literature, the simple diode model is most used. The objective is the parameters extraction of the model to analytically fitting of the experimental measurements. Therefore, the accuracy of parameter values is essential to the study of solar photovoltaic systems. Consequently, the method used for the determination of the parameters plays a primordial role for the resolution of this problem.

Over the years, several methods are used for extracting solar cell parameters. Three main groups of methods are introduced. First, analytical methods are characterized by their simplicity and rapidity of calculation. However, they lack precision since they are based on several hypotheses. We can cite some works such that, the conductance method [1], the five-point and the modified methods [2], ... etc. Secondly, deterministic methods, these methods are very sensitive to the initial values in addition they are demanding at the level of differentiability and convexity such that Newton method [3], Newton–Raphson method [4], non-linear algorithm method [5]. Finally, to circumvent the weaknesses of the previous two methods, the meta-heuristic methods were considered as a promising solution for the extraction of PV model parameters. Because these methods do not have strict requirements and are easy to implement.

Most meta-heuristic methods are inspired by the phenomena of nature. They do not need to satisfy the conditions of convexity or differentiability of objective functions. Because of these advantages, different meta-heuristic methods have been applied to solve PV parameter estimation problems. Such as particle swarm optimization (PSO) [6], simulated annealing algorithm (SA) [7], genetic algorithm (GA) [8], pattern search (PS) [9], biogeography based optimization (BBO) [10], Artificial bee colony (ABC) [11], chaotic asexual reproduction (CAR) [12], adaptive differential evolution (ADE) [13], symbiotic organic search (SOS) [14], improved shuffled complex evolution (ISCE) [15], hybrid firefly algorithm and patter search (HFAPS) [16], multi learning backtracking search (MLBTS) [17], firefly algorithm (FA) [18], ant lion optimization (ALO) [19, 28], particle swarm optimization/ adaptive mutation strategy (PSOAMS) [20], improved cuckoo search algorithm (ImCSA) [21], Lambert W function [22],  improved teaching learning based optimization (ITLBO) [23], adaptive differential evolution [24], hybridizing cuckoo search / biogiography based optimization (BHCS) [25] and three point based approach (TPBA) [26], exploiting intrinsic properties [27].

Although these meta-heuristic methods have yielded satisfactory results compared to analytical or deterministic methods, their accuracy and reliability still need to be improved. These methods have certain constraints because a good optimization performance strongly depends on the fine-tuning and the good choice of the parameter search space. For example, if the search space for the parameters is not accurate enough, there is a risk that the optimization performance level will drop. Also, the measurement uncertainty problem has not been considered in the work involving metaheuristic methods. Although the treatment of measurement uncertainties can be considered as an important parameter for the mathematical model of PV.

In this paper, we propose an approach to improve the extraction performance of the parameters of a double diode PV model based on the ALO meta-heuristic algorithm. We will introduce the notion of measurement uncertainties in order to reduce the search interval of the parameters to be estimated. The proposed approach for extracting parameters is based on three steps. First, the extraction of the parameters is done without considering the uncertainties. Then, we will estimate the uncertainties of each parameter. Finally, the extraction of the parameters will be done instantly taking into account the results found in the other steps. For the validation of the proposed method, we have considered the experimental data of silicon solar cell RTC France [4]. The results are compared to other well-established parameter extraction algorithms in the literature. The results indicate that the proposed method is significantly more accurate than the other methods.

2 Problem formulation and main results

2.1 Preliminary

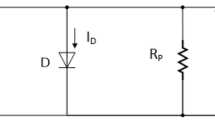
Before proceeding to the parameter extraction phase, it is essential to have a mathematical model that accurately represents the electrical characteristics of the solar cell. Although many equivalent circuit models have been developed and proposed over the past four decades to describe the behaviour of solar cells. In this article, we are interested in the 7 parameters model. The equivalent circuit of the double diode model illustrated by Fig. 1, the solar cell under illumination is modelled as a photocurrent source, two diodes and two parasitic resistors such as

Fig. 1

Equivalent circuits of double diode model

2.2 The classic metaheuristic extraction solar cell parameters method

In this paper, our goal is to extract the parameters of the equivalent circuit shown in Fig. 1. The equivalent circuit can be represented in the form of an analytical equation such as:

$$\begin{aligned} \hat{I}_{L} = I_{ph}- I_{{d}_{1}}-I_{{d}_{2}}- I_{sh} \end{aligned}$$

(1)

where $\hat{I}_{L}$ denotes the estimated output current, $I_{ph}$ denotes the photo generated current. $I_{sh}$ is the shunt resistor current. $I_{{d}_{1}}$ and $I_{{d}_{2}}$ represents the diodes current. The terms $I_{sh}$, $I_{{d}_{1}}$ and $I_{{d}_{2}}$ of equations (1) are expressed as follows:

$$\begin{aligned} I_{{d}_{1}}&= I_{{sd}_{1}}\left[ \hbox {exp}\left( \frac{V_{L}+R_{s} I_{{L}_{mes}}}{n_{1}V_{t}}\right) -1\right] \end{aligned}$$

(2a)

$$\begin{aligned} I_{{d}_{2}}&= I_{{sd}_{2}}\left[ \hbox {exp}\left( \frac{V_{L}+R_{s} I_{{L}_{mes}}}{n_{2}V_{t}}\right) -1\right] \end{aligned}$$

(2b)

$$\begin{aligned} I_{sh}&= \frac{V_{L}+R_{s}I_{{L}_{mes}}}{R_{sh}} \end{aligned}$$

(2c)

$$\begin{aligned} V_{t}&= \frac{kT}{q} \end{aligned}$$

(2d)

where $I_{{sd}_{1}}$ and $I_{{sd}_{2}}$ denotes the saturation current, $V_{L}$ denotes the output voltage, $I_{{L}_{mes}}$ denotes the measured output current, $R_{s}$ denotes the series resistance, $n_{1}$ and $n_{2}$ denotes the diode ideal factor and $R_{sh}$ the shunt resistance. $V_{t}$ denotes the thermal voltage of the diode such that k is the Boltzmann constant $(1.3806503\times 10^{-23}$ J/K), q is the electron charge $(1.60217646\times 10^{-19}$ C) and T is the cell temperature (K).

It is observed from Eqs. (1–2) that if we know the values of $I_{ph}$, $I_{{sd}_{1}}$, $I_{{sd}_{2}}$, $R_{s}$, $R_{sh}$, $n_{1}$ and $n_{2}$, then the I–V characteristic of this model can be constructed. Therefore, accurate extraction of these seven unknown parameters is the core of this study. Over the years, several methods have been used to solve the problem of solar cell parameters extraction. In this paper, the estimation problem is formulated as a nonlinear optimization problem. The ALO algorithm is used to estimate the parameters by minimizing a preselected objective function.

$$\begin{aligned} F=\min \limits _{X \in [lb\quad ub]}\sqrt{\frac{1}{N}\sum \limits _{i=1}^{N}(f(V_{L}(i), I_{{L}_{mes}}(i),X))^{2}} \end{aligned}$$

(3)

where

$$\begin{aligned}&f(V_{L},I_{{L}_{mes}},X)=I_{{L}_{mes}}-\hat{I}_{L}\nonumber \\&\quad =I_{{L}_{mes}} -\left( I_{ph}- I_{{sd}_{1}}\left[ \hbox {exp}\left( \frac{V_{L}+R_{s}I_{{L}_{mes}}}{n_{1}V_{t}}\right) -1\right] \right. \nonumber \\&\qquad \left. -\,I_{{sd}_{2}}\left[ \hbox {exp}\left( \frac{V_{L}+R_{s}I_{{L}_{mes}}}{n_{2}V_{t}}\right) -1\right] - \frac{V_{L}+R_{s}I_{{L}_{mes}}}{R_{sh}}\right) =0 \end{aligned}$$

(4)

where $X=[ I_{ph},\, I_{{sd}_{1}},\,I_{{sd}_{2}},\, R_{s},\, R_{sh},\, n_{1},\,n_{2}]$ represent the vector of unknown parameters, N is the number of data points, $l_{b}$ and $u_{b}$ are the lower and upper bounds on parameter vector X.

The objective function must be minimized with respect to the parameter set. Theoretically, the objective function should be zero when the exact values of the parameters are obtained. But this objective is practically impracticable since there is continuously some unexpected with respect to the operator such as “noise, unknown inputs, etc ...”. In addition, the smaller the objective function, the more satisfying the solution.

2.3 Proposal of extraction of the uncertainties of the parameters

Obtaining an objective value of reality without error is naturally infeasible. This leads us to conclude that any experimental measure is infected with errors. The errors are part of the measurement process. In this situation, the study of experimental results becomes more difficult to obtain. In purchase to increase the performance of this analysis, we will introduce the concept of uncertainty. Consequently, the correct way to state the result of the measurement is to give the best estimate of the quantity and the range within which you are confident the quantity lies. Based on these notions, we can write the following form:

$$\begin{aligned} I_{{L}_{mes}}=\hat{I}_{L} \pm \delta I_{L} \end{aligned}$$

(5)

$\delta I_{L}$ represent the measurement uncertainty of $I_{L}$. Taking into account Eq. (5), the expression of $I_{L}$ can be bounded by the following range:

$$\begin{aligned} I_{1_{mes}}=I_{{L}_{mes}}- \varDelta I_{L} \le I_{{L}_{mes}} \le I_{{L}_{mes}}+ \varDelta I_{{L}}=I_{2_{mes}} \end{aligned}$$

(6)

where $\varDelta I_{L}$ is the measurement uncertainty norm of $I_{L}$ such that $\varDelta I_{L}= \sqrt{\sum \nolimits _{i=1}^{N}(I_{{L}_{mes}}(i)-\hat{I}_{L}(i))^{2}}$. Now, we suppose that the expressions $I_{1}$ and $I_{2}$ can be expressed as equations that depend on the uncertainties $\varDelta I_{ph}$, $\varDelta I_{{sd}_{1}}$, $\varDelta I_{{sd}_{2}}$, $\varDelta n_{1}$, $\varDelta n_{2}$, $\varDelta R_{s}$ and $\varDelta R_{sh}$ such that

$$\begin{aligned} \hat{I}_{1}&= (\hat{I}_{ph}-\varDelta I_{ph})\nonumber \\&\quad - \,(\hat{I}_{{sd}_{1}}-\varDelta I_{{sd}_{1}})\left[ \hbox {exp}\left( \frac{V_{L}+(\hat{R}_{s}-\varDelta R_{s})I_{{L}_{mes}}}{(\hat{n}_{1}-\varDelta n_{1})V_{t}}\right) -1\right] \nonumber \\&-\,(\hat{I}_{{sd}_{2}}-\varDelta I_{{sd}_{2}})\left[ \hbox {exp}\left( \frac{V_{L}+(\hat{R}_{s}-\varDelta R_{s})I_{{L}_{mes}}}{(\hat{n}_{2}-\varDelta n_{2})V_{t}}\right) -1\right] \nonumber \\&- \,\frac{V_{L}+(\hat{R}_{s}-\varDelta R_{s})I_{{L}_{mes}}}{(\hat{R}_{sh}-\varDelta R_{sh})} \end{aligned}$$

(7a)

$$\begin{aligned} \hat{I}_{2}&= (\hat{I}_{ph}+\varDelta I_{ph})\nonumber \\&\quad -\, (\hat{I}_{{sd}_{1}}+\varDelta I_{{sd}_{1}})\left[ \hbox {exp}\left( \frac{V_{L}+(\hat{R}_{s}+\varDelta R_{s})I_{{L}_{mes}}}{(\hat{n}_{1}+\varDelta n_{1})V_{t}}\right) -1\right] \nonumber \\&\quad -\,(\hat{I}_{{sd}_{2}}+\varDelta I_{{sd}_{2}})\left[ \hbox {exp}\left( \frac{V_{L}+(\hat{R}_{s}+\varDelta R_{s})I_{{L}_{mes}}}{(\hat{n}_{2}+\varDelta n_{2})V_{t}}\right) -1\right] \nonumber \\&\quad - \,\frac{V_{L}+(\hat{R}_{s}+\varDelta R_{s})I_{{L}_{mes}}}{(\hat{R}_{sh}+\varDelta R_{sh})} \end{aligned}$$

(7b)

where $\hat{I}_{ph}$, $\hat{I}_{{sd}_{1}}$, $\hat{I}_{{sd}_{2}}$, $\hat{R}_{s}$, $\hat{n}_{1}$, $\hat{n}_{2}$ and $\hat{R}_{sh}$ are the estimated of parameters $I_{ph}$, $I_{{sd}_{1}}$, $I_{{sd}_{2}}$, $R_{s}$, $n_{1}$, $n_{2}$ and $R_{sh}$ respectively, these estimations are determined previously using the optimization problem (4).

We note that the uncertainties $\varDelta I_{ph}$, $\varDelta I_{{sd}_{1}}$, $\varDelta I_{{sd}_{2}}$, $\varDelta n_{1}$, $\varDelta n_{2}$, $\varDelta R_{s}$ and $\varDelta R_{sh}$ are bounded by the interval $[0 \; , \; \varDelta I_{L}]$. Now, our objective is to estimate the uncertainties. In this context, we consider the following objective function:

$$\begin{aligned}&f_{1}(V_{L},I_{{L}_{mes}},\hat{X},\varDelta X)\nonumber \\&\quad =\min \limits _{\varDelta X \in [0\quad \varDelta I_{L}]}\sqrt{\frac{1}{N}\sum \limits _{i=1}^{N}\left( (I_{1_{mes}}(i)-\hat{I}_{1}(i))^{2}+(I_{2_{mes}}(i)-\hat{I}_{2}(i))^{2}\right) } \end{aligned}$$

(8)

At this level of paper, an estimate of the parameters and their uncertainties were obtained. As a consequence, a new search interval of the unknown parameters can be obtained, such that:

$$\begin{aligned} \hat{X}-\widehat{\varDelta X}\le X \le \hat{X}+\widehat{\varDelta X} \end{aligned}$$

(9)

where $\hat{X}=[ \hat{I}_{ph} \;,\; \hat{I}_{{sd}_{1}}\;,\; \hat{I}_{{sd}_{2}}\;,\; \hat{R}_{s}\;,\; \hat{R}_{sh}\;,\; \hat{n}_{1}\;,\; \hat{n}_{2}]$ denotes the estimated of unknown parameters vector, $\widehat{\varDelta X}=[\widehat{\varDelta I_{ph}}\;,\;\widehat{\varDelta I_{{sd}_{1}}}\;,\;\widehat{\varDelta I_{{sd}_{2}}}\;,\;\widehat{\varDelta R_{s}}\;,\;\widehat{\varDelta R_{sh}}\;,\;\widehat{\varDelta n_{1}}\;,\;\widehat{\varDelta n_{2}}]$ denotes the estimated of uncertainties parameters vector.

2.4 Instant solar cell parameter extraction proposal

Now, we will propose a new concept that is used to extract the instantaneous values of each unknown parameters. To do this, we will consider the new parameters limitation interval described in (9). In addition, we will consider a new optimization problem such that:

$$\begin{aligned} f_{2}(V_{L},I_{{L}_{mes}},X)=\min \limits _{X \in [\hat{X}-\widehat{\varDelta X}\quad \hat{X}+\widehat{\varDelta X}]}\sqrt{\frac{1}{N}\left( I_{{L}_{mes}}(i)-\hat{I}_{L}(i)\right) ^{2}} \end{aligned}$$

(10)

3 The Ant lion Optimization

The ant lion optimization is a algorithm inspired by the antlion hunting mechanisms [28]. This algorithm essentially describes the procedure adapted by antlions to hunt the ants. The Antlions create pits or cone-shaped holes for the purpose of trapping ants, antlions are more likely to catch ants when the hole is larger (Fig. 2). In the ALO algorithm, the positions of ants and antlions are randomly initialized. Equation (11) ensures the presence of random walks in the confined research space.

$$\begin{aligned} X^{t}_{k}=\frac{(X^{t}_{k}-a_{k})(b_{k}-c^{t}_{k})}{d^{t}_{k}-a_{k}}+c_{k} \end{aligned}$$

(11)

where $a_{k}$ and $b_{k}$ are the minimum and maximum of random walks for kth variable, respectively; $c_{k}^{t}$ and $d_{k}^{t}$ are the lower bound and upper bound of kth variable at tth iteration, respectively. The ants walk in hyper spheres described by vectors c and d around a selected ant lion.

$$\begin{aligned} c^{n}_{k}&= antlion^{n}_{k}+c^{n} \end{aligned}$$

(12a)

$$\begin{aligned} d^{n}_{k}&= antlion^{n}_{k}+d^{n} \end{aligned}$$

(12b)

When the ant is trapped, the ant lion push the sand into the center of the pit. This prevents the ant from escaping and reduces the radius of the random walk of the ants, as shown below.

$$\begin{aligned} c^{n}&= \frac{c^{n}}{J} \end{aligned}$$

(13a)

$$\begin{aligned} d^{n}&= \frac{d^{n}}{J} \end{aligned}$$

(13b)

where $c^{n}$ and $d^{n}$ indicate the minimum and maximum of all variables at the nth iteration. The constant J is equal to ($J = 10^{w}$ Nn), n is the current iteration and N is the total number of iterations and w is a constant. These two equations guarantee the exploitation by shrinking the radius of updating ant.

Fig. 2

Sand pit trap of an antlion

4 Results and discussions

In this work, the ALO is applied to estimate the uncertain parameters of the double-diode model of silicon solar cell RTC France cited in [4] such that:

The measurements are performed on a 57 mm diameter commercial (R.T.C France) silicon solar cell. Their experimental I–V data are acquired under controlled conditions from an automated measurement system with a CBM 8096 microcomputer acting as a controller. These measurements are obtained under the following conditions 1 sun (1000 W/m$^{2}$) at 33 $^{\circ }$C. For reasonable comparison, the search range of each parameter is given in Table 1. Additionally, the proposed algorithm was compared with four recent algorithms: (BHCS, 2019) [25], (ITLBO, 2019) [23], (ImCSA, 2018) [21] and (HFAPS, 2018) [16]. We consider the following ALO algorithm parameters such that population size $Npop=10$, the maximum number of iterations $maxIt=250$ and 30 independent executions were performed to study the statistical performance of the proposed algorithm.

Table 1 The boundaries of extracted parameters

4.1 Silicon solar cell RTC France

Our objective is the extraction of the silicon solar cell parameters RTC France using the development proposed in this article. the extraction procedure is composed of three steps such that: the first step consists of extracting parameters using the classical method (without consideration of measurement uncertainties). Then, based on the results obtained in the first step. the extraction of the partial uncertainties of the parameters will be the objective of the second stage. Finally, the third step will be dedicated to the extraction of these parameters in an instantaneous way.

4.1.1 Step 1: Extraction of solar cell parameters with the classical method

Taking into account Eqs. (3 and 4), the objective function must be minimized to obtain an optimal set of parameters to characterize the solar cell. Table 2 shows the extracted parameters from experimental data of a silicon solar cell.

Table 2 Parameter extraction with classical method

4.1.2 Step 2: Extraction of uncertainties of solar cell parameters

After estimating the parameters using the classical method, we now proceed to the extraction of uncertainties of measurement specific to each parameter. Taking into account table (2), Eqs. (7) and the operating intervals of the uncertainties of parameters $[0 \; , \; \varDelta I_{{L}}]$ such that $\varDelta I_{L}= \sqrt{\sum \nolimits _{i=1}^{N}(I_{{L}_{mes}}(i)-\hat{I}_{L}(i))^{2}}= 0.011291$. On the basis of the objective function (8) and the ALO algorithm, we obtain the following values of the partial uncertainties Table 3.

Table 3 gives satisfactory RMSE, we note that the uncertainties are significant for the values of the $I_{ph}$ parameters. This remark can be explained by the presence of disturbance in the light source. Based on these results (Table 3), we can define new operating intervals for the parameters of the solar cell such that (Table 4):

Table 3 Extraction of uncertainties of solar cell parameters

Table 4 The new operating intervals of the solar cell parameters

Figure 3 shows that the curve of $I_{L}$ always remains delimited by the curves $\hat{I}_{1}$ and $\hat{I}_{2}$, which validates the approach proposed in this article.

Fig. 3

Evolution of $I_{L}$ , $I_{1_{mes}}$, $I_{2_{mes}}$ curves and their estimated

4.1.3 Step 3: Instant solar cell parameter extraction proposal

We will now proceed to the extraction of the parameters in an instantaneous way taking into account their uncertainties. To do this, we will consider the new parameters limit interval (Table 4) and the objective function described in (10). We thus obtain the following values of the parameters (Table 5): From Table 5, we note the values of the $I_{ph}$ parameters vary practically in each iteration, which can be explained by the presence of disturbance affecting the light source. On the other hand, the other parameters are practically constant throughout the simulation.

Table 5 Uncertain parameter extraction of silicon solar cell RTC

Fig. 4

Evolution of $I_{L}$ , $I_{1_{mes}}$, $I_{2_{mes}}$ curves and their estimated

Figure 4 shows the effectiveness of the method proposed in the article since there is a good convergence of the curve $\hat{I}_{L}$ towards the real curve $I_{L}$.

Remark 1

For the representation of the $\hat{I}_ {L}-V$ curve, it is just replace the values ($I_{ph}$, $I_{sd}$, n, $R_{s}$ and $R_{sh}$) of Table 5 and Experimental Data I and V in Eqs. 1 and 2 for the modeling of the solar cell. In Table 6, the RMSE of the proposed approach is given by the data of $\hat{I}_{L}$ and $I_{L}$.

4.1.4 Statistical study

Furthermore, in order to achieve a higher confidence level of comparison results, 30 independent runs of uncertain ALO are implemented for parameter extraction. Table 6 shows that the proposed algorithm keeps the same performance for each execution.

Table 6 The statistical study of the proposed algorithm

4.1.5 Comparison among various parameter estimation algorithms

Now, the proposed algorithm will be compared to other recent works. According to Table 7, one notices the performance of the work proposed in this article is vastly superior to other work.

Table 7 Comparison of proposed algorithm with other algorithms for the Silicon solar cell RTC

5 Conclusion

In this paper, we proposed a method for estimating parameters of the seven parameters PV model based on the ALO algorithm. The proposed algorithm takes into account the problem of measurement uncertainties to minimize the search interval of the parameters to be estimated. the proposed algorithm determines the instantaneous values of the parameters taking into account the measurement uncertainties of each parameter. We applied the proposed approach to solve the problem of parameter estimation for the real solar cell (silicon solar cell RTC France). Based on the experimental results, we conclude that the proposed method has much better performance than well-established algorithms in the literature.