Effect of the isothermal fins on the natural convection heat transfer and flow profile inside a vertical channel with isothermal parallel walls

Abstract

This paper presents current study on a natural laminar convection flow in vertical plane of open on both ends parallel channel bounded by isothermal walls having the same temperature. An isothermal fins are mounted inside the channel in its walls and located in the middle of the channel face to face also. A numerical investigation has been performed at different parameters of Raleigh number of Ra = 5 × 10³:5 × 10⁶, fin length l/W = 0:0.1:0.2:0.3:0.4, fin angle θ = 0°:7°:15°:22°:30°, and − 30°, and staggered fins of 0, h/3, 2 h/3. The effect of these parameters on the flow structure, velocity distribution, temperature field, local and overall heat transfer coefficient are potted at the mid width and different height along the channel in this work. The numerical analysis have conducted using finite volume integrated proposed by CFDRC depending on the governing equations of mass, momentum, and energy conservation and dimensionless group of heat transfer is used in investigation with a control volume.

1 Introduction

Many applications deals with natural convection arise from open vertical channel walls. The channel walls maintained at higher temperature than flowing fluid. Due to difference in temperature, the buoyant forces are responsible for the arising flow inside the channel. The hot fluid moves upward and departures the outlet of the channel and the cold fluid drained to the channel bottom. The nature of the fluid motion strongly depends on the temperature of the vertical wall. The problem of natural convection inside vertical channel is encountered in both cooling and heating applications. Because the heat transferee using natural convection is a more reliable and low cost cooling method, it encountered in different electronic applications such photo voltaic solar panel cooling. It offered a more life time beside protection for the cooled component. The utilization of fins combined with the high temperature surface should improve the effective of natural cooling.

From the past survey, a great number of experimental and theoretic studies are focused on natural convection flow inside a vertical channel. Desrayaud and Fichera [1] investigated laminar natural convective flows in a vertical isothermal channel with symmetrically rectangular ribs. Their study included ribs position effect on Nusselt number for specified Rayleigh number. They also have studied the length and width of the rib and its influence on the heat transfer. Ahmadi et al. [2] have introduced an analytical model for vertical isothermal fin for the Rayleigh number range between 1000 and 4500. Their study have included effect of temperature difference, and fin aspect ratio on a natural convection heat transfer. They have simulated the problem numerically using ANSYS FLUENT software.

Altaç et al. [3] have studied the heat transfer from horizontal isothermal plate inside a rectangular enclosure. They have performed a numerical parametric study for the effects of the plate length, position and the aspect ratio on a natural convection heat transfer for the Rayleigh number range between 10⁵ and 10⁷. Vazquez et al. [4] have introduced water cooling jacket for a vertical channel in ice-making machine. El-Ghnam [5] has studied natural convection inside vertical open channel without fin. He has numerically investigated the effect of the isothermal channel width and temperature difference on natural convection heat transfer and mass flow rate for the Rayleigh number range between 10 and 10⁸. Sun et al. [6] has numerically analyzed the optimum spacing between vertical isothermal plates cooled by natural, forced or mixed convection. They have concluded that natural convection needed wider spacing than mixed convection according to the pressure drop.

Zoubir et al. [7] has presented a study contracts with natural convection flow in a vertical open-ended channel with wall constant heat flux. The investigations have both conducted or five modified Rayleigh within the range from 1 × 10⁶ to 4 × 10⁷ while solve the Navier–Stokes equations under the Boussinesq assumption. They concluded that the 2d simulation have provided a acceptable prediction for the problem up to Rayleigh 1 × 10⁷ while greater than that value the flow becomes three-dimensional and turbulent. This result seems to be inconsistent to the conclusion stated by Quintiere and Mueller [8]. Fossa et al. [9] has introduced a study on natural convection between two parallel walls. They have investigated uniform heat flux effect on natural convection heat transfer mechanism inside the passage. They have suggested that a suitable channel width has its effect on heat transfer mechanism surface temperature which improved PV efficiency.

Goshayeshi and Ampofo [10] have numerically studied the natural convective between vertical and horizontal surfaces with fins with same temperature. The recommended combination to improve natural cooling was plate located vertically and the vertical fins perpendicular to it. The fin length to width ratio of 25% has provided an considerable enhancement. Da Silva et al. [11] construct a different arrangement for heat source distribution inside vertical channel. Their study has aimed to minimize the temperature at certain points inside the channel (hot spot). They have achieved that optimal heat source arrangement depends strongly with the Rayleigh number. They have recommended optimum heat sources distribution inside channels with forced or natural convection.

Habib et al. [12] has introduced measuring result of natural convection inside vertical channel flow. They have conducted their studies on both symmetric and asymmetric heated wall modes. The results have showed existence of reverse flow at exit region while considering symmetric heated wall mode. The asymmetrical heated wall mode increased the flow field velocities near the hot wall while decreased velocities achieved close to cold plate. Singh et al. [13] has introduced a mathematical solution for natural convective inside vertical channel by solving the governing equations. The problem was limited to incompressible fluid flow only. They have considered asymmetric channel wall temperatures. Their results emphasized development of the rising flow near high temperature wall and down flow near the low temperature wall.

There are also numerous experiments and studies were conducted on similar related problems. La Pica et al. [14] has experimentally studied natural convection heat transfer of air in a vertical channel. Betts et al. [15] has investigated experimentally the natural convection heat transfer of the air as flowing fluid air inside a heated rectangular cavity. Webb et al. [16] has performed experiments to investigate the local heat transfer coefficient for the free convective in heated vertical channel. Keyhani et al. [17] has experimentally studied the natural convection in a vertical channel, with heated and unheated inside sections. Bahrami et al. [18] has experimentally investigated the natural convection heat transfer coefficient of parallel vertical plates. Fedorov et al. [19] has introduced and developed analysis to envisage convinced mass and heat transfer in non-symmetric vertical channel. Ayinde et al. [20] has made measurements for the velocity field in a vertical channel flow. The channel is symmetrically and heated by wall. The measurement conducted using the PIV system (particle image velocimetry). Tanda et al. [21] has performed experiments to govern the natural convective heat transfer coefficient in vertical channels with one flat surface and one roughed surface by introducing oblique ribs. Sparrow et al. [22] has experimentally studied the inter-plate effect on the convection heat transfer inside vertical channel with unheated isothermal walls. Sparrow et al. [23] has investigated experimentally the heat transfer by natural convection in vertical channels with convergent sides. Daloglu et al. [24] has experimentally presented the natural convection in a vertical channel with rectangle cross section. Bhowmik et al. [25] has introduced experiments using water flow to investigate the natural heat transfer coefficient from electronic chips. Hatami [26] has experimentally studied the heat transfer by natural convection in a vertical channel flow with solar air heater. Sparrow et al. [27] has conducted experiment and analysis for natural convection heat transfer in vertical channel with open ended.

Mekheimer [28] studded the influence of heat transfer and magnetic field on the peristaltic flow of Newtonian fluid in a vertical annulus under a zero Reynolds number and long wavelength approximation. The inner tube is uniform, rigid, while the outer tube has a sinusoidal wave traveling down its wall. The flow is investigated in a wave frame of reference moving with velocity of the wave. Numerical calculations are carried out for the pressure rise and frictional forces.

The current work presents numerical investigation for internal laminar natural convection flow in vertical parallel plane open ends channel bounded by symmetric isothermal walls at the same temperature. The simulation considers different values for Raleigh number Ra = 5 × 10³: 5 × 10⁶, fin length l/W = 0:0.4, fin angle θ = 0: ± 30, and staggered fins 0, h/3, 2 h/3. A parametric study for variation of these parameters and their effect on the natural convection inside the channel is the aim of the present work.

2 Theoretical background

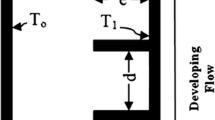
A sketch of the problem is shown in Fig. 1. Two isothermal vertical plates with height h were spaced at a distance w. With constant ratio h/w = 10. The plates are maintained at constant temperature of T_w = T_hot. The temperature at the inlet and out let is considered ambient temperature, where T_w > T_∞. One thin isothermal fin was joined at the middle of each vertical plate. Three parameters were considered, the fin height varied over the spaced distance (l/w = 0, 0.1, 0.2, 0.3, and 0.4), fin angle (90 − θ = 0°, 7°, 15°, 30°, and − 30°), and fin staggered distance (L_s/L = 0, 1/3, and 2/3) as shown in Fig. 2.

Fig. 1

Schematic description of the problem

Fig. 2

The channel with fin stagger distances (L_s/L) variation a Ls/L = 0, b Ls/L = h/3, c L_s/L = 2 h/3

The buoyancy force induces free convection, due to the density and temperature gradients caused by plates heating. In free convection the Nu = f(Gr, Pr). The numerical solution taken place at Pr = 0.69 at T = 400 k, at Rayleigh number of range Ra = 5×10³: 5×10⁶.

The numerical investigations were performed by solving two-dimensional Navier–Stokes equations and energy equation in Boussinesq approximation for change of density [7, 29].

• Mechanisms of heat transfer.

Heat transferred through a stationary medium by vibrational energy of molecules that increase with temperature. According to the Fouriers law the heat flux vector is proportional to the temperature gradient. The heat transport from the solid surface to the moving medium is

$${\text{q}}_{\text{x}} = - {\text{k}}\left( {\frac{{\partial {\text{T}}}}{{\partial {\text{x}}}}} \right)_{{{\text{x}} = 0}}$$

(1)

Convective flux of heat transfer is generally expressed in terms a convective heat transfer coefficient (h) or a Nusselt Number (Nu). According to the Newton’s law of cooling is employed to define the heat transfer coefficient and Nusselt Number. Thus,

$${\text{q}}_{\text{x}} = {\text{h}}_{\text{x}} \left( {{\text{T}}_{\infty } - {\text{T}}_{\text{w}} } \right)$$

(2)

$${\text{h}}_{\text{x}} = {\text{k}}_{\text{f}} \left( {\frac{{\partial {\text{T}}}}{{\partial {\text{x}}}}} \right)_{{{\text{x}} = 0}} /\left( {{\text{T}}_{\infty } - {\text{T}}_{\text{w}} } \right)$$

(3)

$$Nu_{{\rm l}} = \frac{{{\rm h}}_{{\rm x}} {{\rm L}}_{{\rm c}} }{{{\rm k}}_{{\rm f}} }$$

(4)

$$Nu_{\text{l}} = \frac{{{\text{L}}_{\text{c}} }}{{\left( {{\text{T}}_{\text{w}} - {\text{T}}_{\infty } } \right)}}\left( {\frac{{\partial {\text{T}}}}{{\partial {\text{x}}}}} \right)_{{{\text{x}} = 0}}$$

(5)

$$\overline{Nu} = \frac{1}{\text{L}}\mathop \smallint \limits_{0}^{\text{L}} Nu_{\text{L}} {\text{dy}}$$

(6)

The average Nusselt number depends on the grid parameter through the grid density, number of points on the wall, and distances between nodes (∆x) calculated by numerical integration.

$Nu_{l}$	Local Nusselt Number
$h_{x}$	Local heat transfer coefficient at certain point (x)
$k_{f}$	Thermal conductivity for fluid
$\overline{Nu}$	Average Nusselt Number

• The governing equations.

Consider a laminar boundary layer flow that is driven by buoyancy gravity forces as shown in Fig. 1. Assume steady, two- dimensional, constant property conditions in which the gravity force acts in the negative y direction along the channel. Next we apply three fundamental laws to the flow inside the channel through the conservation of mass, conservation of momentum, and conservation of energy to obtain the continuity, momentum, and energy equations for laminar flow in boundary layer.

$$\frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0$$

(7)

$$\rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = \mu \frac{{\partial^{2} u}}{{\partial y^{2} }} - \frac{\partial P}{\partial x}$$

(8)

$$\rho \left( {u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = \mu \frac{{\partial^{2} v}}{{\partial y^{2} }} - \frac{\partial P}{\partial y} + T^{*}$$

(9)

$$\left( {u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y}} \right) = \alpha \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{\vartheta }{{c_{p} }}\left( {\frac{\partial u}{\partial y}} \right)^{2}$$

(10)

Non-dimensional parameters

1. Independent variables	2. velocities	3. Temperature
$x^{*} = {\raise0.7ex\hbox{$x$} \!\mathord{\left/ {\vphantom {x {L_{c} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${L_{c} }$}}$ $y^{*} = {\raise0.7ex\hbox{$y$} \!\mathord{\left/ {\vphantom {y {L_{c} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${L_{c} }$}}$	$u^{*} = {\raise0.7ex\hbox{$u$} \!\mathord{\left/ {\vphantom {u {U_{\infty } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${U_{\infty } }$}}$ $v^{*} = {\raise0.7ex\hbox{$v$} \!\mathord{\left/ {\vphantom {v {U_{\infty } }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${U_{\infty } }$}}$	$T^{*} = \left( {T - T_{w} } \right)/(T_{\infty } - T_{w} )$

Dimensionless group of heat transfer

1. Reynolds Number	2. Prandtl Number	3. Grashof Number
$Re = \frac{{U_{\infty } L_{c} }}{\vartheta }$	$Pr = \frac{\vartheta }{\alpha }$	$Gr = \frac{{gL_{c}^{3} \beta \left( {T_{w} - T_{\infty } } \right)}}{{\vartheta^{2} }}$

• The computational model.

The computational simulation is needed. It gives faster and accurate results while the problem is correctly setup. Solving the flow field variables for low speed and turbulence flow fields is of technical interest. The computational simulation has been applied to different problem configurations [30, 31]. The problem setup has been based on the stated recommendations. A set of boundary condition along the channel can be expressed. The coordinate system shown in Fig. 1 will be used in the solving method where w and h are width and height of the channel respectively. Both walls of the channel remain at the same uniform temperature ($T = T_{w} = T_{hot}$). The velocities and temperature are defined for both inlet and outlet plenum boundaries as $u^{*}$ = 0, $v^{*}$ = 0, and $T = T_{\infty }$.

• The computational grid sensitivity analysis.

Ten computational grids of the clear channel have been studied to ensure grid convergence. The average Nusselt number variation with number of grids is presented in Fig. 3. The grid at which number of cells independent on the results with optimized running time and fast stable convergence equal to 25,000 cells.

Fig. 3

The average Nusselt number variation with number of grids

Numerical simulations have been conducted using three dimensions Navier–Stokes flow solver CFDRC. The simulations were conducted on a computer platform. The study has utilized four different solver modules for geometry, grid generation, computations, parametric study and post processing. The modules is well-ordered using PYTHON scripts files. The solver is multi physics module. It is a pressure based solver. It solves the time-dependent, Reynolds-averaged Navier–Stokes equations for turbulent, compressible flows using a finite volume, time-marching approach on multi-zone, structured grids. Spatial accuracy is nominally second order upwind formulation. the turbulence models considered using the Standard k–ε Model.

The method of finite volume integrated proposed by CFDRC, is used with a control volume of mesh size (125 × 200) in x and y directions respectively for a vertical parallel plates model. The computational mesh employed is shown in Fig. 4 where two vertical plates with a height to width ratio (h/w) including fin at the middle.

Fig. 4

Computational grid a left: complete channel with fin and b right: near fin region

• CFD software validation.

At the beginning, a comparison of the current numerical method for average heat transfer in a clear channel (no fin) of L = 0.1 m, and W = 0.028 m maintained at T_w = 500 k and ambient temperature of 300 K, of dimensionless temperature $\left( {T^{*} } \right)$ at different Rayleigh number. As shown in Fig. 5, the average Nusselts number was plotted against the Rayleigh number at constant h/w. The empirically correlation by Churchill [32] is useful in the calculation of the average Nusselts Number along the vertical isothermal plate.

$$Nu_{L} = 0.68 + \frac{{0.67\left( {Ra} \right)^{1/4} }}{{\left[ {1 + \left( {0.492/Pr} \right)^{9/16} } \right]^{4/9} }}$$

(11)

where the Raleigh Number,

Fig. 5

Current numerical results compared to calculation by Churchill [15]

$$Ra \, = \, Gr \, Pr$$

(12)

This correlation is also recommended by Frank Incropera [33] for the better accuracy obtained for laminar flow. The simulations results indicated maximum deviation between current numerical analysis data and the data of empirical correlation by Churchill [32] within 5%. This gives acceptable level of current numerical method validation.

3 Experimental study

The current numerical was applied for different Raleigh number of Ra = 5 × 10³ and Ra = 5 × 10⁶, with fin height l/w = 0, 0.1, 0.2, 0.3, and 0.4 and fin angle θ = 0°, 7°, 22°, 30°, and − 30° at different sections of the channel y/L = 0%, 25%, 50%, 75%, and 100%. The effect of staggered fin effect is investigated in our numerical solutions also.

Varying the Raleigh Number (Ra) will affect the velocity and temperature profile inside the channel where the channel has no fin on the inside surface. Figure 6 show the velocity profile at different values of y/L starting from the channel inlet y/L = 0 to channel exit y/L = 1. At low Raleigh number (Ra = 5 × 10³, Fig. 6a, the flow is almost stable even near the inlet, and starting from height y/L > 0.25, the profile of longitudinal velocity does not change. On the other hand, at high Raleigh number (Ra = 5 × 10⁶, Fig. 6b, the velocity peaks are higher and velocity at the channel center decreases but still above the inlet centerline velocity and remain almost flat. At all the different values of y/L the peak of the velocity profile appears beside the heated walls as expected, which become sharp and move towards the heated walls with the increasing of Raleigh number. This indicates a rapid acceleration of the fluid near the heated wall.

Fig. 6

Velocity profile along the channel without fin at different sections

As shown in Fig. 7, that the axial dimensionless temperature profiles are plotted at selected dimensionless height y/h for the isothermal vertical smooth walls without internal fin. The temperature besides the isothermal walls is maximum which then drops to the channel center. The temperature profile continues to change with y until the thermal equilibrium with the channel wall. And the fluid temperature increases from the inlet towards the downstream of the channel in all cases due to temperature gradient.

Fig. 7

Temperature distribution along the channel without fin at different sections

At Fig. 7a for low Raleigh Number of Ra = 5 × 10³ with the increase of dimensionless height y/h, the centerline temperature profiles decrease towards the inlet temperature but still above it, and close to parabolic profile at the inlet section. The thermal stabilization takes place faster at low Raleigh number and the fluid is completely warmed up to wall temperature ($T^{*} = 0$). With increasing in Raleigh Number of Ra = 5 × 10⁶ as shown in Fig. 7b all the temperature profiles became wider and mainly horizontal it means that equal to the value of the ambient fluid ($T^{*} = 1$) with thin thermal boundary layer. A fully developed heat transfer flow at the exit is considered and the channel exit temperature is nearly equals to the wall temperature and its distribution is close to stable.

3.1 Effect of fin length

The effect of fin length with variation of l/W on the velocity and temperature distribution at the channel outlet (y = h) are presented in Figs. 8 and 9. Figure 8a shows the velocity profile at different values of fin length (l/W) at the channel exit. The maximum velocity profile appears beside the heated wall as expected for a smooth channel and horizontally at the channel center. With the increase of higher fin length the velocity peaks are sharp and move towards the center. And the velocities become below the inlet centerline velocity. At l/W ≥ 0.3 the separated flow takes place behind the fin causes sharp drop in the velocity profile. Figure 9a shows velocity contour maps inside the channel at different fin height. The velocity contours along the channel were simulated by using CFD.

Fig. 8

Velocity and temperature profiles at the exit of the channel with fin length variation

Fig. 9

a Maps of velocity contours in the channel at different l/W. b Maps of temperature contours in the channel at different l/W

The profiles of the fluid temperature at the channel outlet are shown in Fig. 8b. The dimensional temperature profile ($T^{*} = 0$) appears beside the heated wall, where the fluid is completely warmed up to wall temperature. On the other hand, the dimensional temperature at the exit on the channel axis is close to one i.e. it is equal to the ambient space. With increasing of fin length at l/W = 0.4, the temperature on the axis increase gradually until the wall temperature, due to the fluid separation effect on the mixing in the channel. Figure 9b shows dimensional temperature contour maps inside the channel at different fin height.

The temperature gradient resulted from the mathematical calculations gives an indication that there is a minimum heat transfer at the fin location at y/L = 50%. This temperature gradient decreases also with increasing in the fin length. Table 1, shows that, the results of the mathematical calculations of the temperature gradient at x-direction at different fin length and at different values of y/h starting from the channel inlet y/h = 0 to channel exit y/h = 1. This variation in the temperature gradient effects directly on the Nusselt number.

Table 1 Temperature gradient (dT/dx) at different y/h and l/W

It is clear from Fig. 10 that the centerline velocities along the channel at (x/w = 50%) starting at different inlet velocity. This values decreases with increasing in fin height. For smooth channel, the centerline velocity kept approximated as the inlet velocity. With increasing in y/h % the centerline velocities increase also and intersect at the same value for the cases of l/W ≥ 0.1 with centerline velocity higher than inlet velocity. After y/h ≥ 0.55% the centerline velocities decrease again, but still above the inlet velocity. This refers to throttle effect associated with the fin height.

Fig. 10

Mid width velocity distribution along the channel with fin length variation

As shown in Fig. 11, the centerline temperature distribution along the channel at (x/w = 50%) starting at the same inlet value. The temperature profile almost constant along the center line till y/h = 0.45% with any increasing in fin length l/W and equal to the value of the ambient medium $T^{*}$ = 1. With increasing in y/h more than 0.5%, the dimensional temperature value $T^{*}$ decreases with increasing in the fin length more than l/W = 0.2. With the increase fin length from l/W = 0.2:0.3 the dimensional temperature value decreases with 13%. This drop in the dimensional temperature value reaches to 43% with increasing in the fin length from l/W = 0.3:0.4 due to the thermal stabilization process where the temperature on the axis is lower than in the wall temperature. And the flow separation occurs due to the flow around fin edge.

Fig. 11

Mid width temperature distribution along the channel with fin length variation

3.2 Effect of fin angle (θ)

The effect of fin angle on the velocity and temperature distribution at the channel outlet (y = h) at l/W = 0.4 are presented in Figs. 12 and 13. Figure 12a shows the velocity profile at the channel exit with changing in the fin angle of θ = 0°:7°:15°:22°:30°. The flow profiles are almost the same behavior against the changing in fin angle. The maximum velocity deviation appears at the channel center. With the increase of fin angle from θ = 0°:7°:15°:22°:30° the velocity peaks are increase also from 0.85:0.9:0.95:1:1.05 respectively with sharp profile and move towards the center. The velocities become below the inlet centerline velocity beside the channel wall due to the separated flow which takes place behind the fin causes sharp drop in the velocity profile. Figure 13a shows velocity contour maps inside the channel at different fin angle.

Fig. 12

Velocity and temperature profiles at the exit of the channel with fin angle variation

Fig. 13

a Maps of velocity contours in the channel at different fin angle. b Maps of temperature contours in the channel at different fin angle

The profiles of the fluid temperature at the channel outlet are shown in Fig. 12b. The dimensional temperature profile ($T^{*} = 0$) appears beside the heated wall, where the fluid is completely warmed up to wall temperature. On the other hand, the dimensional temperature at the exit on the channel axis is close to one i.e. it is equal to the ambient space. With increasing of fin angle at l/W = 0.4, the temperature on the axis decrease gradually until the space temperature, due to the fluid velocity effect of the fluid in the channel. Figure 13b shows dimensional temperature contour maps inside the channel at different fin angle

Figure 14 shows the effect of the angle in the opposite direction on the temperature and velocity contours compared to clear fin. The effect of fin angle in the opposite direction θ = − 30° is the same at θ = 30° approximately, with little change in the velocity and temperature at the center axis.

Fig. 14

Temperature and velocity and contours at the exit of the channel with fin angle variation

The behavior of changed of the temperature gradient according to the mathematical calculations gives a similar change in the Nusselt number. Starting with high value that decreases with increasing in y/L reaching to no heat transfer at all and Nu = 0 at y/L = 50%. Table 2, shows that, the results of the mathematical calculations of the temperature gradient at x-direction at different fin angle and at different values of y/h starting from the channel inlet y/h = 0 to channel exit y/h = 1. This variation in the temperature gradient effects directly on the Nusselt number.

Table 2 Temperature gradient (dT/dx) at different fin angle

It is clear from Fig. 15 that the centerline velocities along the channel at (x/w = 50%) starting at little different inlet velocity with l/W = 0.4. A small decrease appears in the velocities values with increasing in fin angle along θ = 0°:7°:15°:22°:30°. A great change in the velocity from 0.4:1.45% of the inlet velocity tacks place at fin edge zone refers to throttle effect. After y/h ≥ 0.5% the centerline velocities decrease again with close values, but still above the inlet velocity.

Fig. 15

Mid width velocity distribution along the channel with fin angle variation

As shown in Fig. 16, the centerline temperature distribution along the channel at (x/w = 50%) starting at the same inlet value. The temperature profile almost constant along the center line till y/h = 0.45% with any increasing in fin angle θ and equal to the value of the ambient medium θ = 1. With increasing in y/h more than 0.45%, the dimensional temperature value θ decreases with increasing in the fin angle. With the increase fin angle from θ = 0°:30° a drop in the dimensional temperature value reaches to 20:30:35:38:40% with increasing in the fin angle from θ = 0°:7°:15°:22°:30° respectively. The flow separation which occurs due to the flow around fin edge related to the changing in the fin angle effect directly on the thermal stabilization process and dimensional temperature value.

Fig. 16

Mid width temperature distribution along the channel with fin angle variation (0:30)

Figure 17 shows the longitudinal temperature and velocity profiles in the different sections (y/L %) for the max fin length (l/W) and max fin angle (θ = 30°).

Fig. 17

Longitudinal temperature and velocity profiles in the different sections (y/h %) at l/W = 0.4 and angle = 30°

3.3 Effect of staggered distance of the fin

At l/W = 0.4 where L_s/L = 0 the separated flow takes place behind the fin causes sharp drop in the velocity profile beside the walls and the maximum velocity takes place at the center axis as shown in Fig. 18. On the other side, with increasing in staggered distance from L_s/L = 0, to h/3, and 2 h/3 the separated flow takes only in on wall side and the peak velocity appears at the other wall side.

Fig. 18

Velocity profiles at the exit of the channel with fin stagger distance (L_s/L) variation

As shown in Fig. 19, the dimensional temperature on the wall increase gradually until the wall temperature, with increasing of staggered distance at maximum fin length the dimensional temperature at the exit on the channel axis is close to one and shifted to the right wall more than the other side due to shifted fin to up.

Fig. 19

Temperature profiles at the exit of the channel with fin stagger distance (L_s/L) variation

4 Results and conclusions

4.1 Effect of the fin angle to local and average Nusselt number

The behavior of local Nusselt number is decreases due to the increase in the fin angle, as it is shown in the Fig. 20a. In the presence of a fin, the heat transfer rate decreases in the braking area before the fin. At the point of fin coupling with the surface, there is almost no flow at the corners, so there is no heat transfer and then Nu = 0. As shown in Fig. 20b, the average Nusselt number decreases with increasing in the fin angle from 0°, 7°, 15°, 22°, to 30°. This decreasing in Nusselt number due to decreasing in heat transfer rate due to throttle are between fins

Fig. 20

a Effect of the fin angle to the local Nusselt number. b Effect of fin angle on the average Nusselt

4.2 Effect of the fin length to local and average Nusselt number

At R_a = 5 × 10⁶, as it shown in Fig. 21a, the behavior of local Nusselt number is decreases due to the growth of the boundary layer thickness, as it is shown in calculations by mathematical calculations. In the presence of a fin, the heat transfer rate decreases in the throttle area at the fin location. At the point of fin coupling with the surface, there is almost no flow at the corners, so there is no heat transfer and then Nu = 0. At the downstream of the fin, there is a symmetrical distribution of local Nusselt number with little decreasing in the heat transfer but does not reach the level of un-separated flow. This is explained by a decrease in the gas flow through the channel with increasing height of the fin. Generally, as fin length increases the average Nusselt number increases also as shown in Fig. 21b.

Fig. 21

a Effect of the fin length to the local Nusselt number. b Effect of fin length on the average Nusselt

5 Conclusion

The numerical results of the laminar free convection inside a vertical duct with isothermal walls have been presented in our paper. This paper presents a parametric variation of fin length-to-channel height (0 to 0.4), fin angle (0° to 30° and − 30°), and fin staggered (0 to 2/3) at R_a = 5 × 10⁶. Temperature distribution and velocity distribution are plotted at different heights along the channel and different width.

The conclusion can be summarized as;

• 1. The empirically correlation is accurate and suitable for the engineering applications in the calculations of the average Nusselts.

• 2. For a clear channel, it was founded that the velocity profiles and temperature distribution along the channel are greatly chanced in various sections of the channel at weak convection of R_a = 5 × 10³. On the other hand, at intense convection of R_a = 5 × 10⁶, there is no heat transfer in the core of the channel out the wall thermal boundary layer which became thinner. There is no change in the velocity profile at various sections except the zone near the walls due to approach the gas temperature to the wall.

• 3. As the fin length increases, the velocity profiles and temperature distribution are greatly deformed along the channel. The heat transfer is improved and the velocity profiles decreases and shrink in the axis as fin height increase.

• 4. At maximum fin height, the velocity profiles became stable in general with little increasing along the channel center line only Leading to decreasing in the rate of heat transfer along the channel center line also.

• 5. The effect of staggered technique in fin, improve the rate of heat transfer beside surface which includes fin, and on the opposite surface gives an opposite effect for absence the other opposite fin on the other surface.

• 6. As fin length is increase the average Nusselt number is increased also. The average Nusselt number is decreased with increasing in the fin angle from 0°, 7°, 15°, 22°, to 30°. But the effect of fin length on the local Nusselt number is greater than the fin angle effect.