Swelling-induced twisting and shearing in fiber composites: the effect of the base matrix mechanical response

Abstract

If a helical network of fibers is embedded in a swellable matrix, and if the fibers themselves resist swelling, then a change in the amount of swelling agent will cause a corresponding twisting motion in the material. This effect has recently been analyzed in highly deformable soft material tubes using the theory of hyperelasticity, suitably modified to incorporate the swelling effect. Those studies examined the effect of spiral angle and fiber-to-matrix inherent stiffness in the context of a ground state matrix material that exhibited classical neo-Hookean behavior in the absence of swelling. While such a ground state material is nonlinear in general, its shear response is linear. As we describe here, it is this shear response that governs the matrix contribution to the twist-swelling interaction. Because gels, elastomers, and even biological tissue can exhibit complex ground state behavior in shear—behavior that may depart significantly from a linear response—we then examine the effect of alternative ground state behaviors on the twist-swelling interaction. The range of behaviors considered includes materials that harden in shear, materials that soften in shear, materials that have an ultimate shear stress bound, and materials that collapse in shear. Matrix materials that either soften or collapse in shear are found to amplify the twisting effect.

1 Introduction

By embedding biassing fibers in a matrix material that is highly absorbant, it is possible to generate specialized deformation modes as the material swells. This is because the fibers naturally guide the deformation in what is essentially a prearranged way. In a previous paper [3], we analyzed this effect in tubes containing spiral patterns of fibers that lie in the plane of the tube’s cross-section. Swelling of the matrix then cause an overall tube twist to take place even though no external forces are applied. Effectively, the internal swelling acts as a body force to induce the twist.

In conjunction with other modes of deformation that can be induced by swelling, such as bending [8] and torsion [1], this suggests that a wide variety of deformation modes could be engendered by intelligent pattern design for fiber biasing [2, 4]. While fiber pattern biassing is inherently a design freedom that could be exploited, other design freedoms should not be overlooked. One of these is the qualitative mechanical behavior of the swellable base material, i.e., the matrix in which the fibers are embedded.

Here it is to be noted that previous studies often focus on matrix behavior that has an essential neo-Hookean type character and which reduces to neo-Hookean behavior in the absence of swelling. While such a ground state material is nonlinear in general, its shear response is linear. As we describe here, it is this shear response that governs the matrix contribution to the twist-swelling interaction. Because gels, elastomers, and even biological tissue can exhibit complex ground state behavior in shear — behavior that may depart significantly from a linear response — it is our purpose here to examine the effect of alternative ground state behaviors on the twist-swelling interaction. The range of behaviors considered includes materials that harden in shear, materials that soften in shear, materials that have an ultimate shear stress bound, and materials that collapse in shear.

To this end, we present the overall continuum mechanics formulation in Section 2 where the focus is on the relevant constitutive treatment for the mechanical behavior due to swelling. The overall twisting boundary value problem of interest is formulated in Section 2. It is in fact a swelling version of what is known as the boundary value problem for azimuthal shear, although for our purposes we often refer to it as twisting of a tube due to swelling. Complexities associated with this boundary value problem, while surmountable numerically as we show in later sections, then lead us to examine a simpler problem, namely swelling-induced shearing of a layer. The main advantage is that the layer problem is one of homogeneous deformation. This simpler problem has many useful analogies to the swelling-induced tube twisting problem. This analogy, and certain basic results, is described in Section 2.

Up to this point in the paper, the matrix material constitutive relation has concentrated on the neo-Hookean type response. A far more general constitutive model for the matrix, which is a swellable version of the Knowles I₁ power law material [6], is introduced in Section 2. The layer problem for homogeneous deformation under swelling is examined thoroughly for this class of materials. We construct curves showing how the layer shears as a function of swelling. This provides certain important insights into how best to approach the tube twisting problem for the case of the power-law matrix material, and a thorough study of this problem is conducted in Section 2. Now curves of layer twisting as a function of swelling are obtained. Both the layer curves and the twisting curves have certain remarkable features. These are discussed and explained in the concluding Section 2.

2 Hyperelastic framework for treating swellable matrices and nonswelling fibers

Our examination is based on swellable hyperelastic materials. We consider materials with a single family of fibers at each material point, where the direction can vary from point to point (as in the spiral fiber patterns considered in [3]).

The swellable hyperelastic materials are treated in terms of the swelling volume constraint $\det \mathbf {F}=v$ where F is the gradient of the deformation mapping from reference locations X to deformed locations x and v is the local swelling value. If v is equal to one everywhere, then this describes an incompressible material. Locations where v > 1 are swollen locations. For a variety of physical processes in soft materials, swelling is determined by chemical or electro-chemical influences that largely decouple from mechanical considerations. In such a case, v can be regarded as a specified field. Moreover, because $\det \mathbf {F}=v$ is a pointwise constraint, the Cauchy stress will contain a constraint reaction pressure − pI where I is the identity tensor and p is the scalar hydrostatic pressure. The value of p is determined directly from the equations of equilibrium in conjunction with the boundary conditions. In particular, as is true for constraint reactions in general, p is not subject to a constitutive prescription.

Once transient effects associated with possible swelling agent diffusion have abated, it is presumed that the equilibrium mechanical response is elastically dominated. The elastic energy density associated with this response is W = W(C,v,X) where C = F^TF is the right Cauchy-Green deformation tensor. The Cauchy stress is then given by

$$ \mathbf{T}= \frac{2}{v}\mathbf{F}\frac{{\partial W}}{\partial \mathbf{C}}\mathbf{F}^{T} -p {\mathbf{I}}. $$

(0.1)

In conjunction with the equilibrium equation

$$ \text{div} \mathbf{T} =\mathbf{0}, $$

(0.2)

this generates partial differential equations that govern the deformation and the pressure field p = p(X). These are to be solved subject to appropriate boundary conditions.

Because we are considering a single direction of fibers at each material point, even though that direction may vary within the material due to fiber patterning, the dependence of W on C is only through the invariants I₁,I₂,I₃,I₄, and I₅. The local swelling condition eliminates I₃ because I₃ = v². The fiber direction itself is specified by a unit vector M in the unswollen reference configuration. The deformed image of this vector is m = FM. The vector m, which is generally not a unit vector, gives the fiber direction in the deformed configuration, and its length gives the local fiber stretch.

In this paper, we restrict attention to materials in which the dependence of W upon $I_{1}, {\dots } I_{5}$ takes the specific form

$$ {W}= w_{m}(I_{1},v)+w_{f}(I_{4}), $$

(0.3)

where w_m and w_f are energy densities associated with matrix and fiber parts respectively. This models fibers that swell very little within a matrix that is able to swell appreciably. In Eq. 0.3, the invariants I₁ and I₄ are given by I₁ = I : C and I₄ = M ⋅CM = m ⋅m. This makes

$$ \mathbf{T}= \frac{2}{v} w_{m}^{\prime}(I_{1},v) \mathbf{B} + \frac{2}{v} {w}_{f}^{\prime}(I_{4}) \mathbf{m} \otimes \mathbf{m} - p \mathbf{I}, $$

(0.4)

where $w_{m}^{\prime }:= \partial w_{m} / \partial I_{1}$ and ${w}_{f}^{\prime }:= \partial w_{f}/\partial I_{4}$, and B is the left Cauchy Green deformation tensor B = FF^T.

An alternative situation, fibers that swell in a matrix that does not appreciably swell, can be described by a converse to Eq. 0.3, W = w_m(I₁) + w_f(I₄,v). For example, this might describe cellulose fibers within a rubbery matrix. However, here our focus is always on Eq. 0.3.

Standard material models in the form of trusted mathematical expressions for w_m and w_f can then be used for mathematical simulation and design modeling. Among these are the forms that we used in our previous work [3] where we considered the well-known neo-Hookean form, suitably modified so as to treat swelling, for the matrix constituent, namely

$$ w_{m}=\frac{1}{2} \mu v^{q} (I_{1}-3 v^{1/3}). $$

(0.5)

Here μ > 0 and q are material constants. Specifically μ is the matrix shear modulus for the nonswollen base material. The parameter q allows for possible modulus variation as a function of swelling. We henceforth disregard that possible effect and so take q = 0 in all equations and discussion going forward.

In [3], we also focussed upon

$$ w_{f}(I_{4})=\frac{1}{ 2} \gamma (I_{4} - 1)^{2}, $$

(0.6)

where γ ≥ 0 is the fiber modulus. The form (0.6) is often referred to as the standard fiber reinforcing model. Whatever form for w_f is chosen, because $\sqrt {I_{4}}$ is the fiber stretch, it is reasonable to require that ${w}_{f}^{\prime }(1)=0$ and ${w}_{f}^{\prime \prime }(I_{4})\ge 0$. These restrictions cause the reference length of the fiber to also be the natural length of the fiber (the length at which it bears no load). On the other hand, there is no similar requirement on the first derivative of w_m as is evidenced by the fact that the neo-Hookean form used in Eq. 0.5 has a constant nonzero first derivative. When Eqs. 0.5 and 0.6 are used together, the dimensionless ratio γ/μ is the essential measure of the relative stiffness of the fiber constituent with respect to the matrix constituent.

In this paper, we retain the form used in Eq. 0.6 for w_f but consider alternative forms for w_m. Attention is restricted to the plane problem. This means that all the displacement and all of the swelling are in an (X,Y )-plane. Such a situation would arise for example if the domain is a uniform cylinder with a general cross-section Ω in the (X,Y )-plane. In the axial direction, say Z, the cylinder is then confined to be between frictionless plates, say at $Z=\pm \frac {1}{2} L$. The fiber direction M is similarly presumed to always lie in the (X,Y )-plane in a manner that is independent of Z. The material and swelling can then vary in the (X,Y ) cross-section while being uniform in Z. This readily realizable state of affairs applies to a potential wide variety of situations and in particular describes the azimuthal shear swelling deformation examined in [3].

3 Swelling and azimuthal shear

We recall the azimuthal shear boundary value problem for tube swelling considered in [3]. The reference domain is an annulus which is described in polar coordinates Ω = {(R,Θ) : A ≤ R ≤ B,0 ≤Θ< 2π}. Here A and B are positive numbers representing the inner and outer radii of the cylinder in the reference configuration. The fiber orientation is also described using polar coordinates

$$ \mathbf{M}= \cos \alpha \mathbf{e}_{R}+\sin \alpha \mathbf{e}_{\varTheta}, $$

(0.7)

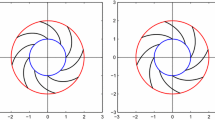
where azimuthal symmetry permits α = α(R). The special case where α is independent of R describes a fiber pattern in the form of a geometric spiral [5]. To illustrate, Fig. 1 shows six equally spaced fiber paths in the unswollen reference configuration when α is independent of R.

Fig. 1

The fibers are continuously dispersed in a spiral pattern. Here 6 equally spaced fiber paths in the unswollen reference configuration are displayed for clarity. A fiber winding angle α that is independent of R makes the fiber pattern a portion of a logarithmic spiral. Here $\alpha = \arctan [1/\log (2)]=55.3^{\circ }$ and B = 2A

Swelling deforms the geometry. Allowing v = v(R) preserves the azimuthal symmetry. The inner surface of the cylinder is presumed to be fixed as would occur, for example, if it were bonded to a rigid cylinder. The outer surface R = B is presumed to be able to freely expand and so traction free boundary conditions are considered on this surface. The just described set up motivates the consideration of the azimuthal shear deformation:

$$ r=r(R), \quad \theta=\varTheta+g(R), $$

(0.8)

where (r,𝜃) are polar coordinate parameters associated with the deformed configuration. The functions r(R) and g(R) need to be determined. No deformation takes place in the third direction, which is formally described by the plane deformation condition z = Z. The boundary conditions for the in-plane deformation on the inner surface are that

$$ r(A)=A, \quad \quad g(A)=0. $$

(0.9)

Boundary conditions due to the traction free outer surface will be clarified later. Clearly, swelling (when v > 1) away from the inner surface will make r(R) > R for locations R > A.

The fully 3-D deformation gradient tensor F for the deformation (0.8) is

$$ \mathbf{F}=r^{\prime}\mathbf{e}_{r}\otimes\mathbf{e}_{R}+ r g^{\prime}\mathbf{e}_{\theta} \otimes \mathbf{e}_{R}+\frac{r}{R}\mathbf{e}_{\theta} \otimes\mathbf{e}_{\varTheta}+\mathbf{e}_{z}\otimes\mathbf{e}_{Z} $$

(0.10)

where the prime ^′ in $r^{\prime }$ and $g^{\prime }$ denotes differentiation with respect to R. Here e_r,e_𝜃,e_z are unit basis vectors in cylindrical polar coordinates of the deformed configuration. Because $\det \mathbf {F}= r^{\prime } r/R$, the local swelling condition $\det \mathbf {F} = v$ gives $r^{\prime } r/R=v$ which can be integrated to yield

$$ r(R)= \sqrt{A^{2} + 2 {{\int}_{A}^{R}} v(\zeta) \zeta d\zeta }. $$

(0.11)

Thus, r(R) is fully determined by the swelling in a manner that is independent of the fiber reinforcing.

At this juncture, it is convenient to introduce λ = λ(R) and k = k(R) via

$$ \lambda= r/R \quad \text{and} \quad k= r g^{\prime}(R). $$

(0.12)

Here λ is the azimuthal stretch, which is known because of Eq. 0.11. In contrast, k is still to be determined. Observe also that the $r^{\prime }$ appearing in Eq. 0.10 can be eliminated by writing $r^{\prime }=v/\lambda$. Direct calculation now gives C, B, m, I₁, and I₄ in terms of λ, k, and v. In particular,

$$ \begin{array}{@{}rcl@{}} \mathbf{B} &=& (v^{2} /\lambda^{2}) \mathbf{e}_{r}\otimes\mathbf{e}_{r}+ (k v /\lambda) (\mathbf{e}_{r} \otimes \mathbf{e}_{\theta}+\mathbf{e}_{\theta} \otimes \mathbf{e}_{r})\\ & & + \left( k^{2} + \lambda^{2}\right) \mathbf{e}_{\theta} \otimes \mathbf{e}_{\theta}+\mathbf{e}_{z}\otimes\mathbf{e}_{z}, \end{array} $$

(0.13)

$$ \mathbf{m}= (v / \lambda) \cos \alpha \mathbf{e}_{r} + (k \cos \alpha+ \lambda \sin \alpha) \mathbf{e}_{\theta}, $$

(0.14)

$$ I_{1}= v^{2} /\lambda^{2} + k^{2}+ \lambda^{2} +1, $$

(0.15)

$$ I_{4}=(v^{2} / \lambda^{2} + k^{2})\cos^{2} \alpha + 2k \lambda\cos \alpha \sin \alpha+ \lambda^{2}\sin^{2} \alpha. $$

(0.16)

The Cauchy stress tensor (0.4) thus takes the form T = T_rre_r ⊗e_r + T_𝜃𝜃e_𝜃 ⊗e_𝜃 + T_zze_z ⊗e_z + T_r𝜃(e_r ⊗e_𝜃 + e_𝜃 ⊗e_r). This is consistent with the frictionless confining plate boundary condition on the fixed Z-surfaces. The in-plane stress components are

$$ T_{rr}=\frac{2 v}{ \lambda^{2} } w_{m}^{\prime} + \frac{2 v}{ \lambda^{2}} \cos^{2} \alpha {w}_{f}^{\prime} - p, $$

(0.17)

$$ T_{\theta \theta}=\frac{2}{v} (k^{2} + \lambda^{2}) w_{m}^{\prime} + \frac{2}{v} \left( k \cos \alpha + \lambda \sin \alpha \right)^{2} {w}_{f}^{\prime} - p, $$

(0.18)

$$ T_{r \theta}=\frac{2 k }{\lambda} w_{m}^{\prime} + \frac{2 }{ \lambda}\cos \alpha \left( k \cos \alpha + \lambda \sin \alpha \right) {w}_{f}^{\prime} . $$

(0.19)

The equilibrium (0.2) in the z-direction is automatically satisfied by taking p = p(R). In the r and 𝜃 directions, the equilibrium equations give

$$ \frac{\partial T_{rr}}{\partial r} + \frac{1}{r} (T_{rr}-T_{\theta \theta})=0, $$

(0.20)

$$ \frac{\partial T_{r \theta}}{\partial r} + \frac{2}{r} T_{r \theta}=0. $$

(0.21)

These are to be solved subject to the free surface condition on R = B, which is simply

$$ T_{rr}(B)=0, \qquad T_{r\theta}(B)=0. $$

(0.22)

The first of these serves as a boundary condition for Eq. 0.20 which in turn serves to determine the pressure field p(R). Because we do not here choose to examine the normal stresses in detail, we need not consider those equations in what follows. Our interest thus focuses on Eq. 0.21, which integrates to T_r𝜃 = c₁r² where c₁ is the integration constant. In view of the second of Eq. 0.22, it then follows that c₁ = 0 and hence that

$$ T_{r \theta}= 0, $$

(0.23)

for all R. Consequently, the Eqs. 0.23 and 0.19 together give

$$ k w_{m}^{\prime}(I_{1},v) + \left( k \cos^{2} \alpha + \lambda \sin \alpha \cos \alpha \right) {w}_{f}^{\prime}(I_{4}) = 0, $$

(0.24)

where I₁ is given by Eq. 0.15 and I₄ is given by Eq. 0.16. In particular, both I₁ and I₄ are quadratic in the unknown k = k(R). On the presumption that Eq. 0.24 is solvable at each location R then, because $k(R)=r g^{\prime }(R)$, one can integrate to obtain the azimuthal shear field g(R) on A ≤ R ≤ B. This in turn gives the overall twist at the outer periphery as ϕ_o = |g(B)|.

Note that if there is no swelling at all (i.e., if v = 1 for all R) then Eq. 0.11 gives r = R making λ = 1 and hence $I_{4}=k^{2} \cos \limits ^{2} \alpha +2 k {\cos \limits } \alpha \sin \limits \alpha +1$. In this case, k = 0 makes I₄ = 1 which causes ${w}_{f}^{\prime }(I_{4})=0$. Thus, k = 0 solves Eq. 0.11 if v = 1 for all R. In other words, if there is no swelling, then there is no shearing.

Equation 0.24 allows for v = v(R) and α = α(R). It is also useful to note that k = 0 solves Eq. 0.24 if either α = 0 or α = π/2. Thus, locations R where the fibers are oriented purely radially or purely azimuthally are not locally sheared.

However, if 0 < α < π/2, then the possible nonlinear nature of $w_{m}^{\prime }$ as a function I₁, and ${w}_{f}^{\prime }$ as a function of I₄, can cause Eq. 0.24 to become a highly nonlinear equation for k = k(R). For the case where w_m and w_f are given by Eqs. 0.5 and 0.6, certain analytical simplifications result, and this was exploited in the methodology of [3].

4 Local analogue: combined biaxial stretch and simple shear with swelling (a simple layer)

The deformation (0.8) described in the previous section is locally one of plane biaxial stretch accompanied by simple shear. We can write such a deformation in a local (X,Y ) coordinate system as

$$ x= \lambda_{x} X+ K Y, \qquad y= \lambda_{y} Y. $$

(0.25)

Here λ_x, λ_y and K are each fixed constants. The local (X,Y )-system identifies X with Θ and Y with R. Because M as given by Eq. 0.7 makes angle α with respect to the R direction, it follows that the locally defined version of M takes the form

$$ \mathbf{M}= \sin \alpha \mathbf{e}_{X}+\cos \alpha \mathbf{e}_{Y}. $$

(0.26)

The deformation gradient tensor F for the deformation (0.25) is given by

$$ \mathbf{F}=\lambda_{x} \mathbf{e}_{x}\otimes\mathbf{e}_{X} + K \mathbf{e}_{x} \otimes \mathbf{e}_{Y} +\lambda_{y} \mathbf{e}_{y} \otimes\mathbf{e}_{Y} +\mathbf{e}_{z}\otimes\mathbf{e}_{Z}. $$

(0.27)

Because $\det \mathbf {F}= \lambda _{x} \lambda _{y}$, the local swelling condition $\det \mathbf {F} = v$ gives λ_y = v/λ_x and we use this to eliminate λ_y in what follows. Using this, we may calculate C, B, and m, the latter two of which become

$$ \begin{array}{@{}rcl@{}} \mathbf{B} &=& ({\lambda_{x}^{2}}+K^{2}) \mathbf{e}_{x}\otimes\mathbf{e}_{x} +K v /\lambda_{x} (\mathbf{e}_{x} \otimes \mathbf{e}_{y} + \mathbf{e}_{y} \otimes \mathbf{e}_{x})\\ & & + v^{2}/{\lambda_{x}^{2}} \mathbf{e}_{y} \otimes \mathbf{e}_{y} + \mathbf{e}_{z}\otimes\mathbf{e}_{z}, \end{array} $$

(0.28)

and

$$ \mathbf{m}= \mathbf{F}\mathbf{M}= (K \cos \alpha+ \lambda_{x} \sin \alpha) \mathbf{e}_{x}+(v / \lambda_{x}) \cos \alpha \mathbf{e}_{y}. $$

(0.29)

Comparing Eqs. 0.27, 0.28, and 0.29 with Eqs. 0.10, 0.13, and 0.14, we note the complete correspondence under the replacements:

$$ (X,Y,Z) \leftrightarrow (\varTheta, R, Z), \quad (x,y,z) \leftrightarrow (\theta, r, z), \quad \lambda_{x} \leftrightarrow \lambda, \quad K \leftrightarrow k. $$

(0.30)

Similar correspondences hold for I₁, I₄, and the stress quantities.

This motivates the consideration of plane-strain shearing of a semi-infinite layer that is also subject to swelling. The reference cross-section in the 2-D plane of interest is now ${\varOmega } = \{(X,Y): -\infty < X< \infty , 0 \le Y \le H \}$ and the fibers are oriented as in Eq. 0.26. As in the azimuthal shear problem, the third Z-direction is constrained, thus rendering the problem planar in the same way. Symmetry with respect to X requires that both v and α must be independent of X.

Boundary conditions must be specified on Y = 0 and Y = H. To put Y = 0 in correspondence with the inner circle R = A in the azimuthal shear problem, we stipulate x = X on Y = 0. For the deformation (0.25), this causes λ_x = 1. The upper surface Y = H is the analogue of the outer circle. However, here we temporarily allow not only expansion in this direction, but also the possibility of a shear traction τ. It is to be noted that dependence of either v or α upon Y is consistent with this scenario. This is analogous to the fact that the azimuthal shear development of the previous section allowed for the possibility of either v or α to depend upon R. For the present layer problem, if either v or α depend upon Y, then λ_y = v/λ_x = v would generally vary as well. All of these conditions would then generally make it necessary to let K = K(Y ) in order to satisfy the equations of equilibrium.

For our purposes here, it is sufficient to restrict attention to v and α that are uniform throughout the layer. Then the homogeneous deformation where K is constant satisfies the equilibrium equations provided that p is also constant. Both the amount of swelling v and the applied shear traction τ enter into the determination of K. The deformation itself is thus specialized from Eq. 0.25 to

$$ x= X+ K Y, \qquad y= v Y. $$

(0.31)

The unit vector M in the fiber direction is deformed into

$$ \mathbf{m}= \mathbf{F}\mathbf{M}= \underbrace{ (\sin \alpha + K \cos \alpha) }_{m_{x}} \mathbf{e}_{x} + \underbrace{(v \cos \alpha)}_{m_{y}} \mathbf{e}_{y}. $$

(0.32)

The value of K is found by requiring that the shear stress T_xy (which is a function of K and v even though it is constant within layer) must match the loading value τ. This condition is

$$ 2K w_{m}^{\prime}(I_{1},v) + 2 \left( K \cos^{2} \alpha + \sin \alpha \cos \alpha \right) {w}_{f}^{\prime} (I_{4}) = \tau $$

(0.33)

with

$$ I_{1}=K^{2}+v^{2}+2, $$

(0.34)

and

$$ I_{4}=(K^{2}+v^{2})\cos^{2} \alpha + 2 K \cos \alpha \sin \alpha+ \sin^{2} \alpha. $$

(0.35)

We have thus arrived at the local analogue problem that is summarized in Fig. 2 as a plane strain swelling deformation of a layer. Both the swelling v and the shear traction τ drive the deformation and so determine K. If there is no shearing (i.e., if K = 0), then swelling (v > 1) expands the layer and elongates the fibers. Shearing (K≠ 0) can counteract this elongation by rotating the fibers. The amount of shear K is determined by the combined action of τ (which acts to shear the matrix) and the fiber rotational tendency (to relieve the fiber elongation). The solution to Eq. 0.33 determines K on the basis of the trade-offs associated with those two effects.

Fig. 2

Combined shearing and stretching of a layer due to applied shear traction τ and overall swelling v. Fibers with original orientation angle α are deformed; this both rotates and stretches them. The deformed orientation angle is α^∗ and the elongational stretch is $\sqrt {I_{4}}$ where I₄ is given by Eq. 0.35

If τ = 0 then v is the sole driving agent for the amount of shear K. Increasing v in the absence of shearing then elongates the fiber. The direction of shearing that reduces this elongation is one that rotates the fibers toward the vertical. Then K > 0 gives clockwise rotation and K < 0 gives counterclockwise rotation. In order to work with K > 0 (clockwise rotation), we shall take − π/2 < α < 0, and this is the situation shown in Fig. 2. For sufficiently small swelling, this rotation can completely eliminate the fiber elongation, however that is energetically costly with respect to the matrix deformation. The optimum value of K as determined by Eq. 0.33 is one that minimizes the combined energetic cost of matrix shearing and fiber elongation.

For − π/2 < α < 0 in the layer problem, the analogous α in the azimuthal shear deformation (0.8) is the positive counterpart, i.e., 0 < α < π/2. This $\alpha \leftrightarrow -\alpha$ correspondence is due to the fact that $(x,y,z) \leftrightarrow (\theta , r, z)$ as indicated in Eq. 0.30, with (𝜃,r,z) in that order, has effectively changed the handedness of the coordinate system.

For the layer deformation (0.31), the effective shear-induced rotation of the fibers causes them to make an angle of α^∗ with respect to the vertical (y-direction), where

$$ \tan \alpha^{*}=\frac{m_{x}}{m_{y}} =\frac{\sin \alpha+K \cos \alpha}{v \cos \alpha}, $$

(0.36)

and we note that the combination K = 0 and v = 1 gives α^∗ = α. In other words, as one would expect, absence of both shearing and swelling preserves the fiber orientation. Also, even without shearing (K = 0), a large swelling can cause α^∗ to formally approach zero because of the v in the denominator of Eq. 0.36.

We now focus on the mechanics of how swelling (v > 1) induces a nonzero amount of shear K without any applied shear traction (τ = 0).

As a first example consider the case where w_m and w_f are given by Eqs. 0.5 and 0.6. These stipulations, along with τ = 0, cause the Eq. 0.33 for K as a function of v to become

$$ \mu K + 2 \gamma \left( K \cos^{2} \alpha + \sin \alpha \cos \alpha \right) (I_{4}-1) = 0 $$

(0.37)

or, in view of Eq. 0.35,

$$ A_{3} K^{3}+A_{2} K^{2}+A_{1} K + A_{0} = 0, $$

(0.38)

with

$$ \begin{array}{@{}rcl@{}} A_{3}=2 \gamma \cos^{4} \alpha, \quad A_{2}=6 \gamma \cos^{3} \alpha \sin \alpha, \end{array} $$

$$ \begin{array}{@{}rcl@{}} A_{1}=\mu - 2 \gamma \cos^{2} \alpha + 2 \gamma v^{2} \cos^{4} \alpha + 6 \gamma \cos^{2} \alpha \sin^{2} \alpha, \end{array} $$

$$ \begin{array}{@{}rcl@{}} A_{0}=-2 \gamma \cos \alpha \sin \alpha + 2 \gamma v^{2} \cos^{3} \alpha \sin \alpha + 2 \gamma \cos \alpha \sin^{3} \alpha. \end{array} $$

If v = 1 this reduces to

$$ \mu K + \gamma \left( 2 K \cos^{2} \alpha (K \cos \alpha + \sin \alpha) (K \cos \alpha + 2 \sin \alpha) \right) =0 $$

(0.39)

and the solution is simply K = 0. More generally for v > 1, this cubic also has one real root K. Beginning with K = 0 when v = 1 the response curve of K vs. v has initial slope

$$ \left.\frac{dK}{dv}\right|_{v=1}= -\left. \left( \frac{1}{A_{1}} \frac{\partial A_{0}}{\partial v}\right) \right|_{v=1}>0 $$

(0.40)

where the sign is based upon taking − π/2 ≤ α ≤ 0. The curves are then monotonically increasing. For very large v, the O(v²) terms in Eq. 0.38 become dominant and one obtains $K \to -\tan \alpha$ as $v \to \infty$. Additional large v analysis of Eq. 0.38 further yields

$$ K = -{\tan \alpha}+\frac{\mu \sec^{4} \alpha \tan \alpha}{2 \gamma}\frac{1}{v^{2}}+o(v^{-2}) \qquad \text{as} \quad v\to \infty. $$

(0.41)

Using this result in Eq. 0.32 gives

$$ \mathbf{m} \sim \frac{\mu}{2 \gamma v^{2}} \frac{\sin \alpha}{\cos^{4} \alpha} \mathbf{e}_{x}+v \cos \alpha \mathbf{e}_{y}, \qquad \text{as} \quad v\to \infty. $$

(0.42)

As the swelling becomes large, not only do the fibers approach a vertical orientation, but they do so in a manner such that m_x = m ⋅e_x → 0.

Figure 3 displays a number of such response curves, all for α = −π/6, showing the effect of the stiffness ratio γ/μ. Each individual response curve approaches the dashed line asymptote $K=-\tan \alpha$ as $v \to \infty$. This approach is more rapid for the graphs with larger γ/μ. As $\gamma /\mu \to \infty$ the associated limiting response is the inextensible fiber limit. In this limit, the response curve is found as the root of the equation I₄ = 1. This causes the cubic equation to degenerate into a quadratic, and K actually attains the value $- \tan \alpha$ when $v = \sec \alpha$ (not as $v \to \infty$). In this inextensible fiber limit, the fibers have become aligned with the y-direction when $v = \sec \alpha$. For the inextensible fiber case, there are no solutions if $v> \sec \alpha$ because then the two conditions of detF = v and I₄ = 1 are incompatible.

Fig. 3

Response curves of K vs. v as given by the roots of Eq. 0.38. Increase in swelling v generates an increased shearing K although there is an upper bounding limit associated with the fully vertical deformed fiber orientation. Panels display different scales for the horizontal axis. Here α = −π/6 and curves are shown for different fiber-to-matrix stiffness ratios γ/μ. The dashed line shows the asymptote as $v \to \infty$ which is given by $K= - \tan \alpha = 0.577$, a value that is common for all of the curves. The approach to this asymptote is more rapid as γ/μ increases

The qualitative nature of the curves shown in Fig. 3 is similar to the response curves shown in Fig. 7 of [3] for the azimuthal shear problem (the twist-swelling problem). This is the anticipated result since a motivation for considering the layer problem is as a simple analogue to the twist-swelling problem. Here it is to be noted that the present X-stretch condition λ_x = 1 is the analogue of a condition that would take λ = r/R = 1 in the twist-swelling problem. For the twist-swelling boundary value problem, the condition λ = 1 holds on the inner radius R = A, however λ > 1 for A < R ≤ B. Thus, the layer problem is most representative of the twist-swelling problem near the inner surface.

5 Power law matrix material and the associated swelling response for the layer

We now examine the effect of the base matrix mechanical behavior on the swelling-shear interaction. In this section, we do this for the layer problem that was just presented in the previous Section 2. Then in the next section, we examine the full azimuthal shear boundary value problem based on an analysis of Eq. 0.24. For these purposes, we continue to consider w_f in the form Eq. 0.6. For w_m we take

$$ w_{m}(I_{1}, v)=\frac{\mu v^{q}}{2b} \left[ \left( 1+\frac{b}{n} (I_{1}-3 v^{2/3})\right)^{n}-1\right] $$

(0.43)

where μ > 0, b > 0, n > 0 and q are material constants. This is a swellable version of the Knowles power law incompressible hyperelastic model presented in [6]. In particular, μ is the infinitesimal shear modulus for the unswollen material. For n = 1 and v = 1, this model reduces to the conventional neo-Hookean material. For n = 1 and general v, it reduces to Eq. 0.5. As was the case with Eq. 0.5, we henceforth take q = 0 in all discussion going forward.

The incompressible (v = 1) version of Eq. 0.43 allows for the consideration of a wide variety of different material qualitative behavior by simply varying the power law parameter n. To see this, consider the layer with no fibers and no swelling. Then the relation between shear stress τ and the amount of shear K is given by Eq. 0.33 upon taking ${w}_{f}^{\prime }=0$ (no fibers) and v = 1 (no swelling) with w_m given by Eq. 0.43. This results in

$$ \tau = \mu \left( 1+ \frac{b}{n} K^{2} \right)^{n-1} K, $$

(0.44)

thus retrieving the original result as given in Eq. 0.27 of [6].

The response behavior given by Eq. 0.44 is indicated in Fig. 4. For n = 1, it gives the well-known linear shear stress response associated with the neo-Hookean form. For n > 1, the result is hardening (the curve steepens). For n < 1, it is softening. For 1/2 < n < 1, this softening still results in $\tau \to \infty$ as $K \to \infty$. For n = 1/2, the shear stress becomes bounded by a finite ultimate stress. For 0 < n < 1/2, the now more exaggerated softening response leads to a collapse in shear wherein the stress response rises to a maximum and then subsequently tends to zero.

Fig. 4

Unswollen shear stress response curves of τ vs. K as given by Eq. 0.44 for the Knowles power law material (μ = 1, b = 1) showing the effect of the power law exponent n

We now consider the swelling layer response, again with a traction free top surface, where w_m and w_f are given by Eqs. 0.43 and 0.6. This provides a generalization of Eq. 0.37 in the form

$$ {\mu K } \left( 1+\frac{b}{n} (I_{1}-3 v^{2/3})\right)^{n-1} + 2 \gamma \left( K \cos^{2} \alpha + \sin \alpha \cos \alpha \right) (I_{4}-1) = 0, $$

(0.45)

where I₁ and I₄ continue to be given respectively by Eqs. 0.34 and 0.35. For n = 1, the Eq. 0.45 reduces to Eq. 0.37.

As before, v = 1 implies K = 0 and we again seek to determine the response curves for K as a function of v. The general case for n≠ 1 leads to a highly nonlinear equation for K as a function of v. There is however one value of n≠ 1 that permits similar analytical progress and that is the case n = 2. For n = 2, the Eq. 0.45 is again cubic in K and so of the general form Eq. 0.38, but now with different coefficients that are given by

$$ \begin{array}{@{}rcl@{}} A_{3}= \frac{1}{4}{b \mu}+ 2 \gamma \cos^{4} \alpha, \quad A_{2}= 6 \gamma \cos^{3} \alpha \sin \alpha, \end{array} $$

$$ \begin{array}{@{}rcl@{}} A_{1}=\frac{1}{4} {\mu} \left( 2+b(2-v^{2/3}+v^{2})\right)+\gamma \left( 2 (v^{2}-1) \cos^{4} \alpha + \sin^{2} (2 \alpha) \right), \end{array} $$

$$ \begin{array}{@{}rcl@{}} A_{0}=\gamma (v^{2} -1 )\cos^{3} \alpha \sin \alpha. \end{array} $$

The initial slope of the response curve is again given by Eq. 0.40 but now making use of the above values for A₁ and A₀. The cubic equation also permits a large v analysis for the n = 2 response and one finds that

$$ K = \underbrace{-\frac{8 \gamma \cos^{3} \alpha \sin \alpha}{b \mu +8 \gamma \cos^{4} \alpha} }_{K_{(\infty, n=2)} } -\frac{24 b \mu \gamma \cos^{3} \alpha \sin \alpha}{(b \mu +8 \gamma \cos^{4} \alpha)^{2}}\frac{1}{v^{4/3}}+o(v^{-4/3}). $$

(0.46)

Thus, as $v \rightarrow \infty$, the n = 2 response curve approaches the asymptote $K=K_{(\infty , n=2)}$. With one limiting exception, this asymptotic value is strictly less than the value $-\tan \alpha$ that was obtained for the n = 1 neo-Hookean case (viz. Eq. 0.41). The limiting exception is the inextensible fiber limit $\gamma /\mu \to \infty$ in which case $K_{(\infty , n=2)} \to -\tan \alpha$.

Using Eqs. 0.46 in 0.32 gives

$$ \mathbf{m} \sim \left( \sin \alpha -\frac{8 \gamma \cos^{4} \alpha \sin \alpha}{b \mu +8 \gamma \cos^{4} \alpha}\right) \mathbf{e}_{x}+v \cos \alpha \mathbf{e}_{y}, \qquad \text{as} \quad v\to \infty. $$

(0.47)

As the swelling becomes large, the fibers again approach a vertical orientation, but now m ⋅e_x = m_x no longer tends to zero.

Figure 5 shows the response curves for both n = 1, n = 2, as well as for several other values of n that do not permit the direct analytical treatment. As in Fig. 3, we take α = −π/6. The horizontal asymptote for n = 2 is evident. Both the n = 2 curve and the n = 3 curve have an internal maximum.

Fig. 5

K versus swelling v as determined by Eq. 0.45 for selected values of n when α = −π/6,γ/μ = 1, and b = 1. The horizontal asymptote for all n ≤ 1 is $K=-\tan (- \pi /6) = 0.577$, exactly as in Fig. 3. The horizontal asymptote for n = 2 is $K= K_{(\infty , n=2)} ={3 \sqrt {3} /11}=0.472$. The maxima for n = 2 and n = 3 occur at v = 4.407 and v = 2.280, respectively. These locations are indicated by ∗ in the figure

6 Azimuthal shear response with the power law matrix material

We now return to the full azimuthal shear problem, where now we use the power law material model (0.43) for the matrix response. The reference fiber angle α and the swelling v are both taken to be uniform (independent of R). The latter in conjunction with Eq. 0.11 gives r(R) in the form

$$ r(R)= \sqrt{A^{2} + v (R^{2}-A^{2})}. $$

(0.48)

The governing equation for g(R) follows by substituting from Eqs. 0.43 and 0.6 into Eq. 0.24 yielding

$$ \begin{array}{@{}rcl@{}} &&\frac{\mu k}{2} \left( 1+\frac{b}{n} (I_{1}-3 v^{2/3})\right)^{n-1}\\ &&{\kern12pt}+ \gamma \cos \alpha \left( k \cos \alpha + \lambda \sin \alpha \right) (I_{4}-1) = 0, \end{array} $$

(0.49)

where I₁ and I₄ are given by Eqs. 0.15 and 0.16 and so also bring in additional terms involving $k=r g^{\prime }(R)$. Thus, Eq. 0.49 is a first-order ODE for g(R) subject to the condition g(A) = 0. When there is neither swelling nor fibers, the corresponding boundary value problem for a tube composed of such a material and subject to an externally imposed twist was studied in [7].

The additional complications due to swelling and the presence of fibers motivated the local analysis of the previous section. It is thus noted that Eq. 0.49 as an ODE for $g^{\prime }(R)$ mirrors the layer Eq. 0.45—which was a scalar equation for the amount of shear K. In particular, the special cases n = 1 and n = 2 give a cubic structure to Eq. 0.49 which facilitates the integration in those two cases.

6.1 Linear response in shear (the neo-Hookean type response, n = 1)

If n = 1, then Eq. 0.43 reduces to the standard neo-Hookean material in the absence of swelling. In particular, material parameter b completely disappears from the constitutive form. When swelling is present, we exactly recover the problem studied previously in [3] and the reader is referred to that work for complete details. For our present purposes, representative results are shown in Fig. 6 for a sequence of deformations corresponding to increasing v. If there was no shearing, then each location would only displace radially, giving the hypothetical fiber locations as shown by the dashed lines. However, the localized shearing, which causes the fibers to elongate less, results in the actual fiber locations as given by the solid lines. Thus there is an overall twist.

Fig. 6

Displaced and deformed fibers for the n = 1 neo-Hookean type matrix taking α = π/6,B/A = 2,γ/μ = 1. The unswollen reference state is on the left (v = 1). Center (v = 8/3) and right (v = 5) show the effect of increasing swelling. The fibers tend to straighten (solid lines) compared with a hypothetical case where there is no localized shearing (dashed lines), imparting an overall twist to the tube

For a given B/A and γ/μ, the outer surface net twist ϕ_o = |g(B)| is dependent on the fiber winding angle α. There is no twist for either radially oriented fibers (α = 0) or circumferentially oriented fibers (α = π/2). Figure 7 shows how twist ϕ_o = |g(B)| varies with α on the interval 0 < α < π/2. For each v, the value of ϕ_o is maximized for some intermediate value of α. This maximizing value of α varies with v as shown in the accompanying table (Table 1).

Fig. 7

Amount of outer surface twist ϕ_o versus fiber winding angle α (both angles in degrees) for selected values of v for the n = 1 neo-Hookean type matrix. Once again B/A = 2 and γ/μ = 1. Table 1 gives values of the maxima. The dashed line shows the upper bound as given by Eq. 0.50

Table 1 The location of maximum outer twist ϕ_o vs. fiber winding angle α (both in degrees) of the five twist-swelling response curves in Fig. 7 (for the n = 1 neo-Hookean type matrix)

The theoretical upper bound value for the twist ϕ_o occurs if the deformed fibers become perfectly radial in orientation. This upper bound value for the outer surface twist g(B) associated with d eformed f ibers that are s traight and r adial (dfsr) is (in radians)

$$ \phi_{o}^{dfsr}= \log(B/A) \tan \alpha. $$

(0.50)

This bounding curve is also shown in Fig. 7. As v increases, the various curves in Fig. 7 approach this upper bound value, albeit in a highly nonuniform fashion in view of “pinning condition” ϕ_o ≡ 0 at α = π/2. In other words, circumferential fibers (α = π/2) give no shearing tendency upon swelling. However, highly inclined fibers (α = π/2 − 𝜖 with 𝜖 > 0 very small but nonzero) become formally unbounded in length as 𝜖 → 0. Straightening these long fibers thus gives a formally unbounded twist ϕ_o in the limit as 𝜖 → 0.

6.2 Stiffening in shear (n = 2)

In the layer analysis of Section 2, the case n = 2 was the other instance of the Knowles power law matrix material that gave analytical simplification. Similarly, the case n = 2 gives certain analytical simplification to the governing Eq. 0.49 because it reduces to

$$ B_{3} k^{3}+B_{2} k^{2}+B_{1} k + B_{0} = 0, $$

(0.51)

where

$$ \begin{array}{@{}rcl@{}} B_{3}= \frac{b \mu}{4}+ \gamma \cos^{4} \alpha, \quad B_{2}=\gamma (2+\lambda) \cos^{3} \alpha \sin \alpha, \end{array} $$

$$ \begin{array}{@{}rcl@{}} &&{}B_{1}=\mu \left( \frac{1+b}{2}-\frac{3b}{4} v^{2/3}+\frac{b}{4} v^{2}\right)\\ &&{\kern12pt}+\gamma \left( (v^{2}-1) \cos^{4} \alpha + 2 \lambda \cos^{2} \alpha \sin^{2} \alpha \right), \end{array} $$

$$ \begin{array}{@{}rcl@{}} B_{0}=\gamma \lambda (v^{2} -1 )\cos^{3} \alpha \sin \alpha. \end{array} $$

Other values of n (other than 1 and 2) when used in Eq. 0.49 give highly nonlinear equations for k (with embedded radical expressions) that require numerical root finding procedures (as considered shortly). However, this n = 2 case permits an explicit solution for k and hence $g^{\prime }$. Numerical integration starting from g(A) = 0 then provides g(R).

Figures 8, 9 and 10 show a sequence of swelling-induced twist deformations corresponding to increasing v. Each figure is analogous to Fig. 6, the difference being that now n = 2 instead of n = 1. For the n = 1 case, the parameter b dropped out. The parameter b does not drop out for the case n = 2, and this accounts for the three separate figures showing the effect of b. Taking n = 2 and b = 1 (Fig. 8) to compare against n = 1 (Fig. 6) shows relatively similar twist behavior, with the n = 2 results lagging somewhat. Increasing b for n = 2 decreases the twist (Fig. 9) while decreasing b increases the twist (Fig. 10).

Fig. 8

Swelling-induced twist taking n = 2 and b = 1 for v = 1,8/3,5. Other parameter values are α = π/6,B/A = 2,γ = 1

Fig. 9

Swelling-induced twist taking n = 2 and b = 10 for v = 1,8/3,5. Other parameter values are α = π/6,B/A = 2,γ = 1

Fig. 10

Swelling-induced twist taking n = 2 and b = 0.1 for v = 1,8/3,5. Other parameter values are α = π/6,B/A = 2,γ = 1

Curves of overall twist as a function of fiber winding angle at fixed v, analogous to the curves in Fig. 7 for n = 1, can also be constructed for the case n = 2. One such set is shown in Fig. 11. These curves are the counterparts to the curves in Fig. 7, but now for n = 2 and b = 1. In particular, we observe how the location of the maxima does not shift as much with v as it did for the n = 1 curves. The theoretical upper bound value for ϕ_o as v increases continues to be given by Eq. 0.50. However, now, in contrast to the n = 1 case, we find that the curves remain well below this bounding value as v increases (Table 2).

Fig. 11

Amount of outer surface twist versus fiber winding angle α for selected values of v for the more general power law matrix material model when n = 2 and b = 1. Table 2 gives values of the maxima. The dashed line shows the upper bound as given by Eq. 0.50

Table 2 The location of maximum outer twist ϕ_o vs. fiber winding angle α (both in degrees) for the five twist-swelling response curves in Fig. 11

The effect of fiber-to-matrix stiffness is shown in Fig. 12. Each curve of twist ϕ_o as a function of swelling v is for a different value of γ/μ, all other parameters being common to all of the curves. As v increases, each curve approaches a separate asymptote, whose ultimate twist value increases as the relative fiber stiffness increases. For example, the ultimate twist value associated with γ/μ = 1 is given by 0.291317 (rad) = 16.69^∘. This value is below the theoretical upper bound value of $\phi _{o}^{dfsr}=0.400189$ (rad) = 22.92^∘ as given by Eq. 0.50. As γ/μ increases, the asymptotes in Fig. 12 move upward and in the limit as $\gamma /\mu \to \infty$ they then approach the value $\phi _{o}^{dfsr}=22.92^{\circ }$. This n = 2 behavior is qualitatively different from that for n = 1. As shown in Fig. 7 of [3], for n = 1 there is a common asymptote for all values of γ/μ. This common asymptote for n = 1 is given by $\phi _{o}^{dfsr}$.

Fig. 12

Amount of outer surface twist versus swelling v for selected values of fiber-to-matrix stiffness ratio γ/μ for the more general power law matrix material model when n = 2, b = 1, α = π/6, and B/A = 2

6.3 Other values of n in Eq. 0.43

When n is different than 1 or 2, the governing Eq. 0.49 is not readily solved for k by algebraic means. Thus a numerical root finding procedure is utilized prior to the numerical integration to obtain g(R). In particular, as g(A) = 0, a recursive tangent line approximations can be used to approximate g(R) for A ≤ R ≤ B. For this purpose, the interval [A,B] is divided into some number of equal subintervals where the size of each interval is dR.

Figures 13 and 14 show the swelling-induced twist deformation for the softening materials with n = 0.75 and n = 0.5, the latter of which is the case with the ultimate shear stress limit. The unswollen (starting) v = 1 configuration is therefore the same as that shown in previous Figs. 6, 8, 9, and 10. A comparison between all of the different presented cases for n is found in Fig. 15 which clearly shows how increasing n decreases the amount of twist. A verification of the numerical solution procedure that generated all of these figures is presented in Fig. 16. That figure shows the convergence of the numerical solution to that obtained by the analytical (algebraic) root finding procedure for the algebraically solvable case n = 2.

Fig. 13

Twist when n = 0.75 and b = 1 for v = 8/3 and v = 5. Other parameter values are α = π/6(30^∘),B/A = 2,γ/μ = 1

Fig. 14

Twist when n = 0.5 and b = 1 for v = 8/3 and v = 5. Other parameter values are α = π/6(30^∘),B/A = 2,γ/μ = 1

Fig. 15

Deformed fiber paths showing outer twist when v = 5 and b = 1 for selected values of n = 0.5,0.75,1,2. Other parameter values are α = π/6(30^∘),B/A = 2,γ/μ = 1

Fig. 16

Verification that the numerical solution procedure converges for the case n = 2 in which algebraic root finding is feasible

By using the above solution procedure, it is then possible to obtain graphs of twist at the outer surface ϕ_o versus swelling v for the full range of n values. In this regard, the graphed information is like that presented in Fig. 12 but now for different exponents n rather than different stiffness ratios. Figure 17 is representative of such graphs, here using the values n = 0.25,0.5,0.75,1,2, and 3. The graphs for n ≤ 1 all approach a common asymptote, and this asymptote is given by $\phi _{o}^{dfsr}$ from Eq. 0.50. In contrast, the cases n = 2 and n = 3 approach asymptotes that are strictly below that theoretical upper bounding value.

Fig. 17

Overall twist at the outer surface ϕ_o versus swelling v for different values of the material power law exponent n = 0.25,0.5,0.75,1,2, and 3. Other parameter values are α = π/6(30^∘),B/A = 2,γ/μ = 1, and b = 1. The fully numerical solution procedure is utilized when n = 0.25,0.5,0.75,3 because analytical root finding is not feasible at those values of n

7 Discussion and conclusions

Whereas previous studies have concentrated on the effect of fiber stiffness and patterning on eliciting complex deformation as a material swells, the present work focuses specific attention on the effect of the base matrix response, i.e., the mechanical behavior of the material in which the fibers are embedded. We show that the base matrix material response also has a significant effect on both simple layer shearing and circular tube twisting as the material swells.

For circular tube twisting, we consider the relative rotation of the tube cross-section when the tube wall contains spirally patterned fibers that proceed from the inner to the outer radius. Because the local deformation is one of simple shear superposed on biaxial deformation, the tube twist findings of Section 2 are anticipated on the basis of certain key understandings of the matrix-fiber-swelling mechanics obtained in Sections 2 and 2 for the more straight forward problem of a simple material layer that swells. For the simpler layer problem, the fibers proceed through the layer cross-section along straight lines. Both horizontally aligned fibers and vertically aligned fibers provide no shearing tendency as the layer swells. However, inclined fibers will cause shearing. In all cases throughout this study, the fibers were modeled on the basis of w_f as given by Eq. 0.6

Section 2 restricted attention to the matrix material model w_m given by Eq. 0.5 with q = 0 and provided the most intuitive key understanding, namely that the generation of shear under simple swelling is due to the presence of fibers, and the effect is magnified as the fibers become relatively stiffer with respect to the matrix. In this case, the ratio γ/μ provided a complete characterization of this relative stiffness. This led to the shear-swelling behavior shown in Fig. 3 with curves for different γ/μ approaching a common asymptote as v becomes large. The rate of approach increased with γ/μ and the common asymptotic value has magnitude $\tan \alpha$. This asymptote is associated with a shearing that places the fibers in the minimal length position, i.e., along the Y axis. Small values of α mean the originally unswollen state involves nearly vertical fibers, and so there is minimal total shearing capacity. Values of α near ± π/2 mean the originally unswollen state involves nearly horizontal fibers and so there is a large shearing capacity and in fact the asymptote’s magnitude $|\tan \alpha |$ becomes unboundedly large because the fibers become unboundedly long as they proceed from Y = 0 to Y = H in the limit as α →±π/2. However, if α = ±π/2 then the fibers are purely horizontal, and there is no shearing tendency because the fibers no longer traverse the layer thickness.

All of these results are mirrored in the tube problem for swelling-induced twist where ϕ_o is the analogue of K and the curves of ϕ_o vs. v are the analogue of the curves of K vs. v for the layer problem. The maximum twisting capacity is now given by $\phi _{o}^{dfsr}$ from Eq. 0.50, which not only involves dependence on α but also on the tube aspect ratio B/A. This is reflective of the fact that the deformed fiber orientation under swelling varies with radius, and every location must have its fibers brought into radial alignment before the twisting capacity is formally exhausted. As in the case of the layer, if w_f and w_m are given by Eqs. 0.6 and 0.5 then the asymptote $\phi _{o}^{dfsr}$ is independent of γ/μ, although it is approached more rapidly as γ/μ becomes large. The asymptotic value is formally zero (no twisting capacity) if the fibers in the unswollen state are already radial (α = 0), whereas the asymptotic value tends to infinity as α →±π/2 because now the unswollen state involves unboundedly large spirals of fiber paths that are nearly circular. However, if α = ±π/2 then the unswollen spirals degenerate to closed perfect circles, and there is no longer any twist under pure swelling, just as the purely horizontal fibers caused the layer problem to lose its shearing tendency.

The above summary results are for w_m given by Eq. 0.5 which means that the matrix has a straightforward linear relation in simple shear between shear stress and the amount of shearing. Polymers, gels, and the ground substance in biological tissue may exhibit far more complex behavior in simple shear, specifically some hardening or softening is not uncommon. Furthermore, under softening, the shear traction may or may not have an ultimate value. Finally, softening may be so severe as to elicit a collapse in shear phenomenon as might occur in phase transition or damage scenarios—either permanent or temporary (reversible/healable).

To investigate these effects, w_m was replaced with Eq. 0.43 where now the power-law exponent n allows a simple distinction between all of these cases. In addition, the special value n = 1 recovers the original model (0.5). The results of Section 2 show these significant effects in the context of the layer analysis. Here it is immediate that matrix hardening (n > 1), at least as it impacts upon the relative fiber-to-matrix stiffness, would correspond to fiber softening. The converse also holds. Thus, increasing n could be expected to have qualitatively similar effects as decreasing γ/μ, and vice versa. This is indeed the case; however, the layer analysis shows that the effect of varying n is in fact more profound. Here the analytical result (0.46) for n = 2 showed that the asymptote itself, not just the rate of approach to the asymptote, was dependent on γ/μ. Moreover, the full shearing capacity — meaning a situation where the asymptotic value of the K vs. v curves for the layer has magnitude$| \tan \alpha |$ — is only achieved as γ/μ becomes unboundedly large. For finite γ/μ, the asymptote height remains below that associated with exhausting this capacity.

This effect is mirrored in the swelling tube findings of Section 2, where Fig. 12 clearly shows how the asymptotes of the various ϕ_o vs. v curves are below the upper bound provided by $\phi _{o}^{dfsr}$. For the n = 2 tube twist problem, because it was the solution to a boundary value problem, we were unable to determine this asymptotic value by pure analysis and so found it numerically. This is in contrast to the layer problem, where the relative simplicity of the homogeneous deformation allowed us to extract the asymptotic value $K_{(\infty , n=2)}<-\tan \alpha$ for finite values of γ/μ.

For values of n different from 1 and 2, we appealed to more extended computational procedures for both the layer and the tube problem. Because n = 1 already gave asymptotes that fully exhausted either the shearing capacity or the twisting capacity, a similar full use of this deformation capacity was found for any n ≤ 1 because by softening the matrix it relatively stiffens the fibers. This can only increase the asymptotes beyond their n = 1 heights. However, since the n = 1 asymptotes already involved full use of the shearing/twisting capacity, such full usage is maintained for n < 1. Thus all the softening cases made use of the full capacity. For this reason, the n ≤ 1 curves in both Figs. 5 and 17 show common upper bound (full usage capacity) asymptotes for the n ≤ 1 cases. Finally, the n = 2 and n = 3 curves in Figs. 5 and 17 also show similar commonality. Now however the n = 2 and n = 3 asymptotes are below that associated with full usage of either layer shearing capacity (Fig. 5) or tube twisting capacity (Fig. 17) as the swelling becomes large.