A Multi-Item Sustainable Manufacturing Model with Discrete Setup Cost and Carbon Emission Reduction Under Deterministic and Trapezoidal Fuzzy Demand

Abstract

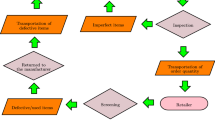
In this paper, the consignor managed inventory model has been developed by the supply of multi-items from the single consignor to the single consignee under the consignment stock policy. The manufacturing process is assumed to be flexible; and therefore, the production rate is treated as a variable. In addition, due to a large number of items, there will be a higher setup cost to install the machinery for the manufacturing process and overproduction leads to the carbon emission. To relieve these two realities, two different reduction functions are made, one of which is made for an economic reason and the other for an environmental reason. A comparison between the two models is established to analyze how the expected cost of the supply chain varies according to the nature of the demand for the product in deterministic and fuzzy environments. Therefore, the purpose of this study is to reduce setup costs, and control carbon emissions during the production of multiple items and at the same time obtaining the minimum expected total cost. Three numerical examples have been considered to examine the two models, and from its results, it has been demonstrated that the minimum total cost can only be achieved when these two reduction functions are considered together. Following this, sensitivity analysis and graphical representation are presented to illustrate the model. At last, managerial insights, the conclusion of this research, and future research directions are provided.

Appendices

Appendix 1

1.1 Special Case

In this case, if both reduction functions are not performed ($\mathcal {S}_{Inv}$ and co_2Invi set to 0), then the integrated cost function will be as follows,

Deterministic Model

$$ \begin{array}{@{}rcl@{}} min~ J_{mr}(.)&=&\sum\limits_{i=1}^{z}\left[\mathcal{S}_{mi}\frac{d_{i}}{nq_{ri}}+\mathcal{O}_{ri}\frac{d_{i}}{q_{ri}}+(h^{f}_{mi}+h^{p}_{mi})\frac{q_{ri}d_{i}}{2{p_{i}}}+\left( \frac{h^{f}_{mi}}{2}+\frac{h^{p}_{ri}}{2}\right)\left( nq_{ri}-(n-1)\frac{q_{ri}d_{i}}{{p_{i}}}\right)+\frac{p_{ci}d_{i}}{{p_{i}}}\right.\\ &&\left.+f_{tr}\left( \frac{d_{i}}{tr_{cap}}\right)+\mathcal{E}m_{tx}\left( (e_{f1}{p_{i}^{2}}-e_{f2}p_{i}+e_{f3})d_{i}+\frac{d_{i}}{tr_{cap}}g_{n}co_{2amt}\right)+\sum\limits_{w=1}^{y}U_{w}co_{2exi,w}\right] \end{array} $$

(46)

where, J_mr(.) = J_mr(n, q_ri, co_2Invi, p_i, co_2aei).

Fuzzy Model

$$ \begin{array}{@{}rcl@{}} min~ J_{D_{mr}}(.)&=&\sum\limits_{i=1}^{z}\frac{1}{6}\left[\left( \mathcal{S}_{mi}\frac{d_{i}}{nq_{ri}}+\mathcal{O}_{ri}\frac{d_{i}}{q_{ri}}+(h^{f}_{mi}+h^{p}_{mi})\frac{q_{ri}d_{i}}{2{p_{i}}}+\left( \frac{h^{f}_{mi}}{2}+\frac{h^{p}_{ri}}{2}\right)\left( nq_{ri}-(n-1)\frac{q_{ri}d_{i}}{{p_{i}}}\right)\right.\right.\\ &&\left.\left.+\frac{p_{ci}d_{i}}{{p_{i}}}+f_{tr}\left( \frac{d_{i}}{tr_{cap}}\right)+\mathcal{E}m_{tx}\left( (e_{f1}{p_{i}^{2}}-e_{f2}p_{i}+e_{f3})d_{i}+\frac{d_{i}}{tr_{cap}}g_{n}co_{2amt}\right)+\sum\limits_{w=1}^{y}U_{w}co_{2exi,w}\right)\right.\\ &&\left.+2\left( \mathcal{S}_{mi}\frac{d_{i}}{nq_{ri}}+\mathcal{O}_{ri}\frac{d_{i}}{q_{ri}}+(h^{f}_{mi}+h^{p}_{mi})\frac{q_{ri}d_{i}}{2{p_{i}}}+\left( \frac{h^{f}_{mi}}{2}+\frac{h^{p}_{ri}}{2}\right)\left( nq_{ri}-(n-1)\frac{q_{ri}d_{i}}{{p_{i}}}\right)\right.\right.\\ &&\left.\left.+\frac{p_{ci}d_{i}}{{p_{i}}}+f_{tr}\left( \frac{d_{i}}{tr_{cap}}\right)+\mathcal{E}m_{tx}\left( (e_{f1}{p_{i}^{2}}-e_{f2}p_{i}+e_{f3})d_{i}+\frac{d_{i}}{tr_{cap}}g_{n}co_{2amt}\right)+\sum\limits_{w=1}^{y}U_{w}co_{2exi,w}\right)\right.\\ &&\left.+2\left( \mathcal{S}_{mi}\frac{d_{i}}{nq_{ri}}+\mathcal{O}_{ri}\frac{d_{i}}{q_{ri}}+(h^{f}_{mi}+h^{p}_{mi})\frac{q_{ri}d_{i}}{2{p_{i}}}+\left( \frac{h^{f}_{mi}}{2}+\frac{h^{p}_{ri}}{2}\right)\left( nq_{ri}-(n-1)\frac{q_{ri}d_{i}}{{p_{i}}}\right)\right.\right.\\ &&\left.\left.+\frac{p_{ci}d_{i}}{{p_{i}}}+f_{tr}\left( \frac{d_{i}}{tr_{cap}}\right)+\mathcal{E}m_{tx}\left( (e_{f1}{p_{i}^{2}}-e_{f2}p_{i}+e_{f3})d_{i}+\frac{d_{i}}{tr_{cap}}g_{n}co_{2amt}\right)+\sum\limits_{w=1}^{y}U_{w}co_{2exi,w}\right)\right. \end{array} $$

$$ \begin{array}{@{}rcl@{}} \phantom{min~ J_{D_{mr}}(.)}&&\left.+\left( \mathcal{S}_{mi}\frac{d_{i}}{nq_{ri}}+\mathcal{O}_{ri}\frac{d_{i}}{q_{ri}}+(h^{f}_{mi}+h^{p}_{mi})\frac{q_{ri}d_{i}}{2{p_{i}}}+\left( \frac{h^{f}_{mi}}{2}+\frac{h^{p}_{ri}}{2}\right)\left( nq_{ri}-(n-1)\frac{q_{ri}d_{i}}{{p_{i}}}\right)\right.\right.\\ &&\left.\left.+\frac{p_{ci}d_{i}}{{p_{i}}}+f_{tr}\left( \frac{d_{i}}{tr_{cap}}\right)+\mathcal{E}m_{tx}\left( (e_{f1}{p_{i}^{2}}-e_{f2}p_{i}+e_{f3})d_{i}+\frac{d_{i}}{tr_{cap}}g_{n}co_{2amt}\right)+\sum\limits_{w=1}^{y}U_{w}co_{2exi,w}\right)\right] \end{array} $$

(47)

where, $J_{D_{mr}}(.)= J_{D_{mr}}(n,q_{ri},co_{2Invi},p_{i},co_{2aei}).$

Appendix 2

The values of Γ₁,Γ₂, and Γ₃ are given in the following:

$$ \begin{array}{@{}rcl@{}} {\Gamma}_{1}&=&\frac{p_{ci}e^{\left( \frac{co_{2Invi}}{\delta}\right)}2+e^{\left( \frac{co_{2Invi}}{\delta}\right)}(h_{ri}^{p}q_{ri}+(h_{mi}^{p}+h_{mi}^{f})q_{ri}+h_{mi}^{f}q_{ri}-h_{ri}^{p}nq_{ri}-h_{mi}^{f}nq_{ri})}{8\mathcal{E}_{m_{tx}}e_{f1}}\\ {\Gamma}_{2}&=&\frac{2p_{ci}e^{\left( \frac{co_{2Invi}}{\delta}\right)}+e^{\left( \frac{co_{2Invi}}{\delta}\right)}(h_{ri}^{p}q_{ri}+(h_{mi}^{p}+h_{mi}^{f})q_{ri}+h_{mi}^{f}q_{ri}-h_{ri}^{p}nq_{ri}-h_{mi}^{f}nq_{ri})}{8\mathcal{E}_{m_{tx}}e_{f1}}\\ {\Gamma}_{3}&=&\frac{e_{f2}^{3}}{216e_{f1}^{3}} \end{array} $$

Appendix 3

The values of β₁ and β₂ are given in the following:

$$ \begin{array}{@{}rcl@{}} {\upbeta}_{1}=&\left( \sqrt{\left( \frac{e_{f2}^{3}}{216e_{f1}^{3}}+{\upbeta}_{2}\right)^{2}-\frac{e_{f2}^{6}}{46656 e_{f1}^{6}}}+\frac{e_{f2}^{3}}{216 e_{f1}^{3}}+{\upbeta}_{2}\right)^{\frac{1}{3}}\\ {\upbeta}_{2}=&\frac{2p_{ci}+q_{ri}(h_{ri}^{p}+(h_{mi}^{p}+h_{mi}^{f})+h_{mi}^{f}-h_{ri}n-h_{mi}^{f}n)}{8\mathcal{E}_{m_{tx}}e_{f1}} \end{array} $$