A Computationally Efficient Inverse Dynamics Solution Based on Virtual Work Principle for Biped Robots

Abstract

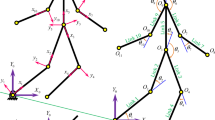
This paper deals with proposing a computationally efficient solution for the inverse dynamics problem of biped robots. To this end, the procedure of developing a closed-form dynamic model using D’Alembert’s-based virtual work principle (VWP) for a biped robot is described. Then, a closed-form inverse dynamics solution is developed during different phases of walking. For a given motion, the closed-form solution is evaluated at each control cycle to yield the joint torques and interaction forces. This procedure is time-consuming for robots with a large number of degrees of freedom such as 3D biped robots. Alternatively, to improve the computational efficiency of the procedure, a method is proposed to solve inverse dynamics efficiently without the need to develop a closed-form solution. In order to show the computational efficiency of the proposed method, its calculation time is compared to the closed-form solutions obtained from the VWP and Lagrange approaches, while this comparison reveals the merit of the proposed method in terms of computational efficiency. For an example application of the proposed solution for inverse dynamics, a dynamic-based optimization procedure is carried out to show the significance of employing toe-off and heel-contact gait phases during biped walking.

Appendix A

In order to generate trajectories for various components of the feet, without loss of generality, we assume that the right foot is in stance phase and the left foot is in swing phase. For the other half of the gait cycle, it is sufficient to change the role of the right and left feet. With this assumption, the boundary conditions and feet trajectories for walking pattern number 1 in Table 1 may be obtained for the right and left feet as:

$$\left\{ {\begin{array}{ll} {x_{r} = X_{bs} } \hfill & {} \hfill \\ {y_{r} = - L_{p} } \hfill & {} \hfill \\ {z_{r} = 0 } \hfill & {} \hfill \\ {\alpha_{r} = 0} \hfill & {, \quad 0 \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ {\beta_{r} = 0 } \hfill & {} \hfill \\ {\gamma_{r} = 0} \hfill & {} \hfill \\ \end{array} } \right.$$

(33)

$$\left\{ \begin{aligned} x_{l} = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{*{20}l} {{x_{l}:} - c + X_{bs} \to X_{bs} + c} \hfill \\ {{\dot{x}_{l}:}0 \to 0\quad \quad \quad \quad \quad \quad \to \mathop \sum \limits_{i = 0}^{5} a_{i} t^{i} , 0 \le t \le t_{s} } \hfill \\ {{\ddot{x}_{l}:}0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {X_{bs} + c, \quad \quad t_{s} \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ \end{array} } \right. \hfill \\ y_{l} = L_{p} ,\quad \quad 0 \le t \le \left( {t_{s} + t_{d} } \right) \hfill \\ z_{l} = \left\{ {\begin{array}{ll} {\left\{ {\begin{array}{ll} {{z_{l}:}0 \to H \to 0} \hfill \\ {{\dot{z}_{l}:}0 \to 0\quad \quad \quad \quad \quad \quad \to \mathop \sum \limits_{i = 0}^{6} b_{i} t^{i} ,\quad \quad 0 \le t \le t_{s} ,} \hfill \\ {{\ddot{z}_{l}:}0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {0, \quad \quad \quad \quad t_{s} \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ \end{array} } \right. \hfill \\ \begin{array}{ll} {\alpha_{l} = 0 ,\quad \quad 0 \le t \le \left( {t_{s} + t_{d} } \right)} \\ {\beta_{l} = 0, \quad \quad 0 \le t \le \left( {t_{s} + t_{d} } \right)} \\ {\gamma_{l} = 0 ,\quad \quad 0 \le t \le \left( {t_{s} + t_{d} } \right)} \\ \end{array} \hfill \\ \end{aligned} \right.$$

(34)

in which $\left( {{\text{x}},{\text{y}},{\text{z}}} \right)$ denotes the position of the foot with respect to the inertial coordinate system and also $\left( {{{\alpha }},{{\beta }},{{\gamma }}} \right)$ specifies the orientation of the foot about x-, y-, and z-axes, respectively. Parameter H is the maximum height to which the swing foot reaches, during SSP. Moreover, Lp is half of the length of pelvis link. For the walking pattern number 2 of Table 1, the boundary conditions are considered as follows, and the feet trajectories can be obtained:

$$\left\{ \begin{aligned} x_{r} = \left\{ \begin{aligned} X_{bs} ,0 \le t \le \left( {t_{s} + t_{md} } \right) \hfill \\ \left\{ {\begin{array}{*{20}l} {x_{r} :X_{bs} \to X_{bs} + l_{s} \left( {1 - cos\beta_{t} } \right)} \hfill \\ {\dot{x}_{r} :0 \to 0\quad \quad \quad \quad \quad \quad \quad \quad \to \mathop \sum \limits_{i = 0}^{5} a_{i} t^{i} ,\quad \quad \left( {t_{s} + t_{md} } \right) \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ {\ddot{x}_{r} :0 \to 0} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned} \right. \hfill \\ y_{r} = - L_{p} ,\quad \quad 0 \le t \le \left( {t_{s} + t_{d} } \right) \hfill \\ z_{r} = \left\{ \begin{aligned} 0 ,\quad \quad 0 \le t \le \left( {t_{s} + t_{md} } \right) \hfill \\ \left\{ {\begin{array}{*{20}l} {z_{r} :0 \to l_{s} sin\beta_{t} } \hfill \\ {\dot{z}_{r} :0 \to 0\quad \quad \to \mathop \sum \limits_{i = 0}^{5} b_{i} t^{i} , \quad \quad \left( {t_{s} + t_{md} } \right) \le t \le \left( {t_{s} + t_{d} } \right),} \hfill \\ {\ddot{z}_{r} :0 \to 0} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned} \right. \hfill \\ \alpha_{r} = 0 , \quad \quad 0 \le t \le \left( {t_{s} + t_{d} } \right) \hfill \\ \beta_{r} = \left\{ \begin{aligned} 0,0 \le t \le \left( {t_{s} + t_{md} } \right) \hfill \\ \left\{ {\begin{array}{*{20}l} {\beta_{r} :0 \to \beta_{t} } \hfill \\ {\dot{\beta }_{r} :0 \to 0\quad \quad \to \mathop \sum \limits_{i = 0}^{5} c_{i} t^{i} ,\quad \quad \left( {t_{s} + t_{md} } \right) \le t \le \left( {t_{s} + t_{d} } \right),} \hfill \\ {\ddot{\beta }_{r} :0 \to 0} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned} \right. \hfill \\ \gamma_{r} = 0 ,\quad \quad 0 \le t \le \left( {t_{s} + t_{d} } \right) \hfill \\ \end{aligned} \right.$$

(35)

$$\begin{aligned} \left\{ {\begin{array}{*{20}l} {x_{l} = \left\{ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {x_{l} : - c + X_{bs} + l_{s} \left( {1 - cos\beta_{t} } \right) \to X_{bs} + c + \left( {l_{as} + l_{ah} } \right)\left( {1 - cos\beta_{h} } \right)} \hfill \\ {\dot{x}_{l} :0 \to 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \to \mathop \sum \limits_{i = 0}^{5} a_{i} t^{i} ,\quad 0 \le t \le t_{s} } \hfill \\ {\ddot{x}_{l} :0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {x_{l} :X_{bs} + c + \left( {l_{as} + l_{ah} } \right)\left( {1 - cos\beta_{h} } \right) \to X_{bs} + c} \hfill \\ {\dot{x}_{l} :0 \to 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \to \mathop \sum \limits_{i = 0}^{5} b_{i} t^{i} ,\quad t_{s} \le t \le \left( {t_{s} + t_{md} } \right) } \hfill \\ {\ddot{x}_{l} :0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {X_{bs} + c \quad ,\quad \left( {t_{s} + t_{md} } \right) \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.} \hfill \\ {y_{l} = L_{p} \quad ,\quad 0 \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ {z_{l} \left\{ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {z_{l} :l_{s} sin\beta_{t} \to H \to \left( {l_{as} + l_{ah} } \right)sin\beta_{h} } \hfill \\ {\dot{z}_{l} :0 \to 0\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \to \mathop \sum \limits_{i = 0}^{6} a_{i} t^{i} , 0 \le t \le t_{s} } \hfill \\ {\ddot{z}_{l} :0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {z_{l} :\left( {l_{as} + l_{ah} } \right)sin\beta_{h} \to 0} \hfill \\ {\dot{z}_{l} :0 \to 0\quad \quad \quad \quad \quad \quad \to \mathop \sum \limits_{i = 0}^{5} b_{i} t^{i} ,\quad t_{s} \le t \le \left( {t_{s} + t_{md} } \right), } \hfill \\ {\ddot{z}_{l} :0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {0,\left( {t_{s} + t_{md} } \right) \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.} \hfill \\ {\alpha_{l} = 0,0 \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ {\beta_{l} = \left\{ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {\beta_{l} :\beta_{t} \to - \beta_{h} } \hfill \\ {\dot{\beta }_{l} :0 \to 0\quad \quad \to \mathop \sum \limits_{i = 0}^{5} a_{i} t^{i} , 0 \le t \le t_{s} } \hfill \\ {\ddot{\beta }_{l} :0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {\beta_{l} : - \beta_{h} \to 0} \hfill \\ {\dot{\beta }_{l} :0 \to 0\quad \quad \to \mathop \sum \limits_{i = 0}^{5} b_{i} t^{i} , t_{s} \le t \le \left( {t_{s} + t_{md} } \right),} \hfill \\ {\ddot{\beta }_{l} :0 \to 0} \hfill \\ \end{array} } \right.} \hfill \\ {0 , \left( {t_{s} + t_{md} } \right) \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ \end{array} } \hfill \\ \end{array} } \right.} \hfill \\ {\gamma_{l} = 0 , 0 \le t \le \left( {t_{s} + t_{d} } \right)} \hfill \\ \end{array} } \right. \hfill \\ \hfill \\ \end{aligned}$$

(36)

where ${{\beta }}_{\text{t}}$ is the angle of foot about toe joint and ${{\beta }}_{\text{h}}$ is the angle of foot about heel. Parameter tmd is assumed to be the half of td. Moreover, Parameter lah is the distance between the ankle and the heel, and las is the distance between the ankle and the center of sole. Furthermore, ${\text{a}}_{\text{i}}$ and ${\text{b}}_{\text{i}}$ and ${\text{c}}_{\text{i}}$ are the polynomial’s coefficients, which may be obtained consistently with the boundary conditions.