Abstract
Horizontal and vertical generating functions and recursion relations have been investigated by Comtet for triangular double sequences. In this paper we investigate the horizontal and vertical log-concavity of triangular sequences assigned to polynomials which show up in combinatorics, number theory and physics. This includes Laguerre polynomials, the Pochhammer polynomials, the D’Arcais and Nekrasov–Okounkov polynomials.
Similar content being viewed by others
1 Introduction
Log-concavity of sequences of numbers, for example binomial coefficients and Stirling numbers, coefficients of polynomials, and values of discrete random variables, is an important characteristic studied in algebra, combinatorics, computer science, number theory, probability and statistical mechanics.
Comtet ([4], Chap. V), recorded horizontal and vertical recurrence relations for triangular sequences, including Stirling numbers of the first kind and of the second kind. This paper investigates horizontal and vertical log-concavity for the Pochhammer polynomials, D’Arcais and Nekrasov–Okounkov polynomials. In several cases the vertical log-concavity fails, but still a vertical C-log-concavity seems to be in place. We refer to a recent paper by Hong and Zhang ([15], see also Sect. 3).
In 2003, Nekrasov and Okounkov [18, 19] discovered a spectacular hook length formula, which comprises building blocks polynomials \(Q_n(x)\) of degree n involving all partitions \(\lambda \vdash n\) of n and the multisets of hook lengths \(\mathcal {H}(\lambda )\):
Shortly after that Westbury [24] and Han [8] also discovered the same formula utilizing different methods. The polynomials \(Q_n(x)\) have non-negative rational coefficients and the sequence of coefficients has no internal zeros. Applying Newton’s theorem could be considered in order to prove log-concavity, if the roots are real, which was conjectured (see Amdeberhan [1]). Recently, Heim and Neuhauser [9] disproved the conjecture. Nevertheless, there is overwhelming numerical evidence that \(Q_n(x)\) is still log-concave. We have used PARI/GP to check this up to \(n=1500\).
Recently, Hong and Zhang [15], supervised by Ono, invested in the log-concavity and unimodality of \(Q_n(x)\). They proved for sufficiently large n that a huge proportion of the coefficients of \(Q_n(x)\) at the beginning of the sequence have the log-concavity property, at the end they are decaying. Additionally, they came up with a conjecture which also implies the unimodality for \(Q_n(x)\) for large n.
In this paper we define families of polynomials \(\{P_n^{g,h}(x)\}_{n=1}^{\infty }\), where g and h are normalized non-vanishing arithmetic functions. Let \(P_0^{g,h}(x)=1\). Then
Although most of the results stated in this paper, assume that \(h \in \{ \mathop {\mathrm{id}},1\}\), we keep the general notation to emphasize the connection by (1) and the hope to come up with more general theorems in the future.
We are interested in particular in the arithmetic functions \( 1(n)=1\), \(\mathop {\mathrm{id}}(n)=n\), \(s(n)=n^2\) and \( \sigma (n)= \sum _{d \vert n} d \). Further, let \(\tilde{g}(n):= g(n)/n\). Note that \(\tilde{1}(n)= 1/n\). Suppose that \(G(T):=\sum _{n=1}^{\infty } g(n) T^n\) is analytic at \(T=0\). We will then have for \(h \in \{ \mathop {\mathrm{id}},1\}\) generating series of exponential and geometric type (see also Corollary 3):
We note that for specific arithmetic functions g, we obtain the Pochhammer polynomials (rising factorials: \(g=1\), \(h=\mathop {\mathrm{id}}\)), associated Laguerre polynomials (\(g=\mathop {\mathrm{id}}\), \(h=\mathop {\mathrm{id}}\)), Chebyshev polynomials of the second kind (\(g=\mathop {\mathrm{id}}\), \(h=1\)), and also polynomials attached to reciprocals of Klein’s j-invariant (\(g\left( n\right) \) is the \(n-1\)st coefficient of Klein’s j-invariant, cf. OEIS sequence A000521, divided by 744, \(h=1\)) and reciprocals of Eisenstein series \(E_k\) of weight k (\(g=\sigma _{k-1}\), \(h=1\)) [11, 13].
Important examples in this paper are the D’Arcais polynomials and the related Nekrasov–Okounkov polynomials. Let \(g(n)= \sigma (n)\) and \(h(n)=\mathop {\mathrm{id}}(n)=n\). Then the D’Arcais polynomials [5, 13, 24] \(P_n^{\sigma , \mathop {\mathrm{id}}}(x)\) are equal to the nth coefficient of the \(-x\)th power of the Dedekind \(\eta \)-function [21]. Nekrasov and Okounkov proved that
Brenti’s result [2], on polynomials with non-negative coefficients and where the sequence of coefficients has no internal zeros, implies that if the D’Arcais polynomials are log-concave then the Nekrasov–Okounkov polynomials also are log-concave. The converse of Brenti’s Theorem is in general not true and it is not generally true for unimodality.
The purpose of this paper is threefold. We first prove that there is a crossover between the coefficients of \(P_n^{\tilde{g},1}(x)\) and \(P_n^{g,\mathop {\mathrm{id}}}(x)\). The crossover transfers log-concavity from \(P_n^{\tilde{g},1}(x)\) to \(P_n^{g,\mathop {\mathrm{id}}}(x)\). Second, suppose that \(A_{n,m}^{g,h}\) is the mth coefficient of \(P_{n}^{g,h}(x)\). Suppose that m is fixed, then we examine the vertical log-concavity with respect to n. Hong and Zhang [15] defined a property which could still be true, when the vertical log-concavity fails. Let us name this new property vertical C-log-concavity (see Sect. 3). Finally we raise a question on horizontal and vertical C-log-concavity on the double sequence of coefficients of \(\{P_n^{g,h}(x)\}_{n=1}^{\infty }\), where \(h=1\) or \(h=\mathop {\mathrm{id}}\).
2 First results
Suppose that g is a normalized arithmetic function. We say that g is of moderate growth if G(T) is analytic at \(T=0\). Further, suppose that h is a normalized non-vanishing arithmetic function. We then have for \(n\ge 1\):
Here \(A_{n,n}^{g,h} = 1/\prod _{k=1}^n h(k)\) and \(A_{n,1}^{g,h}= g(n)/h(n)\). Moreover, suppose that the values of g and h are positive integers, then
It is difficult to obtain results like (4) for arbitrary pairs (g, h). Since \(P_n^{\mathop {\mathrm{id}}, \mathop {\mathrm{id}}}\left( x\right) \) has only real roots, but some of the Nekrasov–Okounkov polynomials, e. g. \(Q_{10}(x) = P_{10}^{\sigma , \mathop {\mathrm{id}}} (x+1)\) have also non-real roots [9], it is obvious, that some results only work maybe for specifically chosen pairs. It is not clear to us if the following conversion principle can be stated in a more general form.
Theorem 1
(Conversion Principle) Suppose that g is a normalized arithmetic function of moderate growth. Then
Example 1
We have \(P_n^{1,1}(x) = x (x+1)^{n-1}\) for \(n\ge 1\). This implies that
This further implies that \(P_n^{\mathop {\mathrm{id}}, \mathop {\mathrm{id}}}(x) = \frac{x}{n} L_{n-1}^{(1)}\left( -x\right) \), where \(L_n^{(\alpha )}(x)\) is the associated Laguerre polynomial of degree n with parameter \(\alpha \) ([6], Chap. 3). Note that (5) gives conceptional proof of Theorem 2 in [10]; see also [13]. Recall that \(L_n^{(\alpha )}(x)\) for \(\alpha >-1\) are orthogonal polynomials and solutions of the differential equation
Before we prove Theorem 1 we provide some applications.
Corollary 1
Suppose that \(P_n^{\tilde{g},1}(x)\) is log-concave, then \(P_n^{g,\mathop {\mathrm{id}}}\,(x)\) is log-concave.
We can also fix m and consider the sequence \(\{ A_{n,m}^{g,h}\}_n\). If this sequence is log-concave for all m we say that \(\{P_n^{g,h}(x)\}_n \) is vertically log-concave.
Corollary 2
\(\{ P_n^{\tilde{g},1}(x)\}_n \) is vertically log-concave iff \(\{P_n^{g,\mathop {\mathrm{id}}}\,(x)\}_n \) is vertically log-concave.
Proof of Theorem 1
We call \(\mathcal {E}_g(T):= \sum _{n=1}^{\infty } \frac{g(n)}{n} \, T^n\) the (modified) Eichler integral of G(T). In the case of \(g(n)= \sigma (n)\) and \(T= q := \text {e}^{2 \pi \text {i} \tau }\), where \(\tau \) is in the upper complex half-plane, \(\mathcal {E}_g(T)\) is the Eichler integral of \(\frac{1-E_2}{24}\) of the weight 2 quasi-modular Eisenstein series \(E_2(\tau )\). We refer to [3] for recent work on Eichler integrals.
We prove that for all \(m \in \mathbb {N}\):
The strategy of the proof is the following. We consider the x expansion of \(\sum _{n=0}^{\infty } P_{n}^{g,h}(x)\, T^n\) for \(h \in \{\mathop {\mathrm{id}}, \, 1 \}\). In the domain of absolute convergence we interchange two infinite sums and compare the coefficients. The core of the proof is the transition from the exponential series to the geometric series. The formula utilizing the geometric series is given by
This can be directly verified by comparing the Cauchy product of the two power series \(\sum _{n=0}^{\infty } P_{n}^{\tilde{g},1}(x)\, T^n \) and \(1- x \, \mathcal {E}_g(T)\) and the defining recursion formula of \(P_{n}^{\tilde{g},1}(x)\).
The formula utilizing the exponential series is given by
Suppose that the generating series \(\sum _{n=0}^{\infty } P_{n}^{g, \mathop {\mathrm{id}}}(x)\, T^n \) is denoted by \(F_g(x,T)\). First, we observe that the recursion formula (1) is encoded in the functional equation
Further, let \(f(n):= \sum _{d \vert n} \mu (d) \, g(n/d)\), where \(\mu \) is the Moebius function. Then it can be shown by a standard procedure (logarithmic differentiation), that the Euler product
satisfies the functional equation (6). Finally, since
the proof has been completed. \(\square \)
From this proof we obtain the exponential and geometric realization of \(P_n^{g,h}(x)\).
Corollary 3
Let \(h=\mathop {\mathrm{id}}\) or \(h=1\), then we have identities (2) and (3) for the assigned generating series:
3 Log-concavity and double sequences
Definition 1
Suppose that \(\left\{ a_n\right\} _{n=0}^{\infty }\) is a sequence of non-negative real numbers. A finite sequence is extended with zeros.
-
(1)
The sequence is called log-concave if \(a_n^2 \ge a_{n-1} \, a_{n+1}\) for \(n \ge 1\).
-
(2)
We denote a double sequence \(\mathcal {A}=\{a_{n,m}\}\) horizontally log-concave iff for every \(n_0 \in \mathbb {N}\) the sequence \(\{a_{n_0,m}\}\) is log-concave and vertically log-concave iff for every \(m_0 \in \mathbb {N}\) the sequence \(\{a_{n,m_0}\}\) is log-concave.
-
(3)
If for \(C>1\) fixed and for all \(m_0\) the sequence \(\{a_{n,m_0}\}_{1 \le n \le C^{m_0}}\) is log-concave, then we denote the double sequence \(\mathcal {A}\) as vertically C-log-concave.
We are mainly interested in double sequences \(\mathcal {A}=\{a_{n,m}\}\) of triangular shape: \(a_{n,m}=0\) for \(m>n\) or \(m=0\), and \(a_{n,m}\) are otherwise positive.
Suppose that g and h are normalized arithmetic functions with positive real values. Suppose that g is of moderate growth. Then we assign to the family of polynomials \(P_n^{g,h}(x)\) the double sequence \(\mathcal {A}^{g,h}=\{a_{n,m}^{g,h}\}\) of triangular shape by putting
and otherwise zero. If \(\mathcal {A}^{g,h}\) is horizontally or vertically log-concave or vertically C-log-concave we give \(P_n^{g,h}(x)\) the same label. We are interested in the D’Arcais polynomials \(P_n^{\sigma , \mathop {\mathrm{id}}}(x)\) which are conjectured to be horizontally log-concave. In the next section we provide counter-examples for vertical log-concavity and put this observation in the context of a conjecture by Hong and Zhang [15], addressing the vertical C-log-concavity.
Let us first give some examples, which may serve as a source of ideas to prove the Hong and Zhang conjecture. Example 1 leads to:
Proposition 1
Let \(g(n)=h(n)\) equal to 1(n) or \(\mathop {\mathrm{id}}\left( n\right) \). Then the assigned double sequences \(\mathcal {A}^{1,1}\) and \(\mathcal {A}^{\mathop {\mathrm{id}}, \mathop {\mathrm{id}}}\) are horizontally and vertically log-concave.
Proof
We recall that
Then \(\mathcal {A}^{1,1}\) consists of binomial coefficients, and therefore are (horizontally) log-concave. Binomial coefficients are also vertically log-concave:
Horizontal and vertical log-concavity of \(\mathcal {A}^{1,1}\) implies by Corollary 1 and Corollary 2 the proof of the proposition. This could also be obtained by a direct calculation. \(\square \)
Example 2
Let \(s\left( n\right) =n^2\). We recall from [10] that
We obtain:
Proposition 2
The double sequences \(\mathcal {A}^{\mathop {\mathrm{id}},1}\) and \(\mathcal {A}^{s, \mathop {\mathrm{id}}}\) are horizontally and vertically log-concave.
Proof
It is sufficient to show that the double sequence \(\{ \left( {\begin{array}{c}n+m-1\\ 2m-1\end{array}}\right) \}_{n,m}\) is horizontally and vertically log-concave. This is shown in a straightforward manner.\(\square \)
Example 3
The polynomials \(n! \, P_n^{1,\mathop {\mathrm{id}}}(x)\) are obtained by the raising factorials. We have
Suppose that \(S\left( n,m \right) = \left[ \begin{array}{c} n \\ m \end{array} \right] \) is the unsigned Stirling number of the first kind and \({\widetilde{1}}(n) = \frac{1}{n}\). Then
Recall that the unsigned Stirling numbers of the first kind satisfy a three term recursion formula, similar to the recursion formula of binomial coefficients:
This example is quite interesting. As a first result we have:
Proposition 3
The double sequences \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) and \(\mathcal {A}^{\tilde{1}, 1}\) are horizontally log-concave but not vertically log-concave.
Proof
The double sequence \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) is horizontally log-concave according to the theorem by Newton. To prove that the double sequence \(\mathcal {A}^{\tilde{{1}}, 1}\) is horizontally log-concave we cannot apply Newton’s theorem, since we do not know if \(P_n^{\tilde{{1}},1}(x)\) has only real roots. \(\mathcal {A}^{\tilde{{1}}, 1}\) is horizontally log-concave iff
Since \(S\left( n,m\right) =0\) only for \(m\le 0\) or \(m\ge n+1\), the Eq. (7) is true for \(m\le 1\) and \(m\ge n\).
For the rest of this part of the proof we now assume \(2\le m\le n-1\), which implies that all in (7) involved Stirling numbers are non-zero. From this we obtain
Sibuya ([23], Corollary 3.1) has shown that (8) holds strictly which proves our claim.
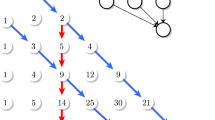
To disprove the vertical log-concavity, we record the coefficients of the first six polynomials \(P_n^{1, \mathop {\mathrm{id}}}(x)\).
\(n! \, {A}_{n,m}^{1, \mathop {\mathrm{id}}}\) | \(m=6\) | \(m=5\) | \(m=4\) | \(m=3\) | \(m=2\) | \(m=1\) |
|---|---|---|---|---|---|---|
\(n=6\) | 1 | 15 | 85 | 225 | 274 | 120 |
\(n=5\) | 0 | 1 | 10 | 35 | 50 | 24 |
\(n=4\) | 0 | 0 | 1 | 6 | 11 | 6 |
\(n=3\) | 0 | 0 | 0 | 1 | 3 | 2 |
\(n=2\) | 0 | 0 | 0 | 0 | 1 | 1 |
\(n=1\) | 0 | 0 | 0 | 0 | 0 | 1 |
Let \(m=1\), then \(n_0=2\) is the smallest n, such that
fails. Moreover, (9) fails for all \(n \ge 2\).
Let \(m=2\), then \(n=n_0=5\) is the smallest n, such that
fails.\(\square \)
Remark
From ([14], Example 2.3) we obtain \(P_{n+1}^{1,\mathop {\mathrm{id}}}\left( x\right) =\frac{n+x}{n+1}P_{n}^{1,\mathop {\mathrm{id}}}\left( x\right) \). There is no obvious finite recursion formula for \(P_{n}^{\tilde{{1}},1}\left( x\right) \).
In the following we show that also in the case of \(m=2\) the inequality (10) fails for all \(n \ge n_0=5\). Let \(H(n)=\sum _{k=1}^n \frac{1}{k}\) denote the nth harmonic number. The sequence of harmonic numbers is log-concave. It is easy to see that
Thus, \(A_{n,2}^{\tilde{{1}}, 1} = \frac{2}{n} \, H(n-1)\). We study the function
Since \(H(n)= H(n-1) + \frac{1}{n}\), we obtain:
Let \( n \ge 2\). We have for \(2\le n\le 4\) the bounds \(1\le H\left( n-1\right) <2\). Thus,
Otherwise, \(H(n-1) >2\), which leads to
4 On Hong and Zhang’s conjecture
Recently, Hong and Zhang [15] presented an interesting conjecture which implies that the Nekrasov–Okounkov polynomials are unimodal for large n.
4.1 Nekrasov–Okounkov polynomials
In 2003 Nekrasov and Okounkov, in an arXiv preprint ([18], formula (6.12)), announced a remarkable new type of hook length formula, based on their work on random partitions and the Seiberg–Witten theory (final publication [19]). Shortly after their discovery, Westbury [24] and Han [8] also spotted the hook length formula in connection with the Macdonald identities. Westbury utilized properties of twisted universal characters and Han properties of t-cores.
The hook length formula relates the sum over products of partition hook lengths [7, 17] to the coefficients of complex powers of Euler products [12, 20, 22], which is essentially a power of the Dedekind eta function.
Suppose that \(\lambda \) is a partition of n denoted by \(\lambda \vdash n\) with weight \(|\lambda |=n\). We denote by \(\mathcal {H}(\lambda )\) the multiset of hook lengths associated to \(\lambda \) and by \(\mathcal {P}\) the set of all partitions. The Nekrasov–Okounkov hook length formula is given by
The identity (11) is valid for all \(z \in \mathbb {C}\). The Dedekind eta function \(\eta (\tau )\) is given by \(q^{\frac{1}{24}} \prod _{m=1}^{\infty } \left( 1 - q^m \right) \) (see [21]). In [9] we revised and refined three conjectures posted by Amdeberhan [1]. The formula (11) is built up of a family of polynomials \(Q_n(x)\). The nth Nekrasov–Okounkov polynomial is given by
Note that all the coefficients of \(Q_n(x)\) are non-negative. Suppose that \(Q_n(x)\) has only real roots (previous Conjecture 2), then we know already from Newton that this implies that \(Q_n(x)\) is log-concave, and hence unimodal (previous Conjecture 3). We disproved Conjecture 2, and used PARI/GP to check that \(Q_n(x)\) is log-concave for \(n \le 1500\). Note that the roots of \(Q_n(x)\) are directly related to the Lehmer conjecture [12, 16].
4.2 D’Arcais polynomials
In 1913 D’Arcais [5] studied a sequence of polynomials \(P_n(x)\) (which are denoted D’Arcais polynomials [24]):
The coefficients are called D’Arcais numbers [4]. Newman and Serre [20, 22] studied the polynomials in the context of modular forms. Serre proved his famous theorem on lacunary modular forms, utilizing the factorization of \(P_n(x)\) for \( 1 \le n \le 10\) over \(\mathbb {Q}\).
4.3 Hong and Zhang’s conjecture
Hong and Zhang [15] investigated a conjecture, published by Heim and Neuhauser [9] on the unimodality of the Nekrasov–Okounkov polynomials and the related log-concavity (see also [1]).
We consider the generating series
Let \(m \in \mathbb {N}\). We denote by \(b_{m,n}\) the coefficients of the q-expansion of the mth power of f(q) and we put otherwise \(b_{m,n}=0\). We follow [15] with \(m=k\) and \(b_{m,n}= c_{n,k}\).
Conjecture
(Hong, Zhang) There exists a constant \(C>1\), such that for all \(m \ge 2\) and \(1 \le n \le C^m\):
At the end of their paper they offer evidence and also remark that it is very likely that \(C=2\) may fulfill their conjecture. Finally, they prove that the validity of their conjecture implies that the Nekrasov–Okounkov polynomials are unimodal for large degrees.
4.4 Vertical version of the Hong–Zhang conjecture
The following identity puts the numbers \(b_{m,n}\) in the context of double sequences derived by polynomials defined by the recursion (1). We consider the q-expansion of reciprocal power series [11], induced by normalized arithmetic functions g, which provides the link to the polynomials \(P_n^{g,1}(x)\):
Thus, the numbers \(b_{m,n}\) are the mth coefficients of the polynomial \(P_n^{\tilde{\sigma }, 1} (x)\). The duality property shows that \(b_{m,n}/m!\) is also equal to the mth coefficients \(A_{n,m}\) of the D’Arcais polynomials. Hence, we immediately obtain:
Theorem 2
Let \(C>1\). The Hong–Zhang conjecture with \(C>1\) is true iff the double sequence \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) attached to the D’Arcais polynomials is vertically C-log-concave iff the double sequence \(\mathcal {A}^{\widetilde{\sigma }, 1}\) is vertically C-log-concave.
5 Open challenges and further study
Suppose that g is a normalized positive real-valued arithmetic function of moderate growth. We consider double sequences \(\mathcal {A}^{g,h}\) assigned to families of polynomials \(P_n^{g,\mathop {\mathrm{id}}}(x)\) and \(P_n^{g,1}(x)\) for \(h=\mathop {\mathrm{id}}\) or \(h=1\). The horizontal and vertical log-concavity of sequences are important characteristics. We utilize a conversion principle, Theorem 1, which provides an explicit translation from the double sequences \(\mathcal {A}^{g, \mathop {\mathrm{id}} }\) to the double sequence \(\mathcal {A}^{\tilde{g},1}\).
5.1 Unsigned Stirling numbers of the first kind
Let \(g=1\) and \(h={\mathop {\mathrm{id}}}\). Then the double sequence \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) assigned to
is horizontal log-concave. We have already shown that the vertical log-concavity fails. Nevertheless, numerical investigation shows similarities to the Hong–Zhang conjecture. We have recorded this in the following Table 1.
Proposition 4
For large n the sequence \(\frac{S\left( n,m\right) }{n!}\) is not log-concave.
In the proof we will use Landau’s big O notation for functions on an unbounded subset of the positive real numbers and \(f\left( x\right) =O\left( g\left( x\right) \right) \) if there is a \(C>0\) and an \(x_{0}\) such that \(\left| f\left( x\right) \right| \le Cg\left( x\right) \) for all \(x\ge x_{0}\). We also will need the polynomials \(v_{m}\left( y\right) \) of degree m defined by the power series expansion of \(\frac{\text {e}^{xy}}{x\Gamma \left( x\right) }=\sum _{m=0}^{\infty }v_{m}\left( y\right) x^{m}\).
Proof
From [25] we can deduce that \(\frac{S\left( n,m\right) }{n!}=\frac{v_{m-1}\left( \ln \left( n-1\right) \right) }{n}+O\left( n^{\varepsilon /2-2}\right) \) for any \(0<\varepsilon <1\). Then
Now \(\ln \left( n-1\pm 1\right) =\ln \left( n-1\right) +\ln \left( 1\pm \frac{1}{n-1}\right) =\ln \left( n-1\right) +O\left( n^{-1}\right) \). Since \(v_{m-1}\left( y\right) \) is a polynomial we have \(v_{m-1}\left( \ln \left( n-1\pm 1\right) \right) =v_{m-1}\left( \ln \left( n-1\right) \right) +O\left( n^{-1}\right) \). Together this yields
Therefore its sign is determined by the sign of
\(\square \)
Challenge 1
Is the double sequence \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) vertically C-log-concave?
We expect that the answer to this question will also give some insight in the Hong–Zhang conjecture.
5.2 D’Arcais polynomial version of Hong–Zhang’s conjecture
Hong and Zhang [15] considered the coefficients \(b_{m,n}\) of the mth power of the generating series
and conjectured that there exists a \(C>1\), such that for \(m \ge 2\) and \(1 \le n \le C^m\):
We have proven in this paper that the conjecture is equivalent to the vertical C-log-concavity of the D’Arcais polynomials \(P_n^{\sigma , \mathop {\mathrm{id}}}(x)\) given by
Challenge 2
Assume \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) horizontally log-concave. Does this imply the Hong–Zhang conjecture?
5.3 D’Arcais polynomials
The Nekrasov–Okounkov \(Q_n(x)\) polynomials are shifted D’Arcais polynomials. We have checked numerically that for \(n \le 1500\) the D’Arcais polynomials are (horizontally) log-concave. We would reinforce the conjecture stated in [1] and [9] on the unimodality of the Nekrasov–Okounkov polynomials.
Challenge 3
(Conjecture) The double sequence \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) assigned to the D’Arcais polynomials is horizontally log-concave.
By Brenti’s result this implies the log-concavity of the Nekrasov–Okounkov polynomials and therefore also the unimodality.
5.4 Examples for horizontal and vertical C-log-concavity
To get a better understanding of the D’Arcais polynomials it would be beneficial to know which property of the input function \(g=\sigma \) enforces the horizontal and vertical properties of the double sequences \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) and \(\mathcal {A}^{\tilde{\sigma }, \mathop {\mathrm{1}}}\).
Challenge 4
Characterize the set of normalized positive-valued arithmetic functions, which provide horizontally and vertically (C-)log-concave properties of the assigned double sequences.
References
Amdeberhan, T.: Theorems, problems and conjectures.arXiv:1207.4045v6 [math.RT] (2015)
Brenti, F.: Log-concave and unimodal sequences in algebra, combinatorics, and geometry: an update. In: H. Barcelo, G. Kalai (eds.) Jerusalem Combinatorics ’93: An International Conference in Combinatorics, May 9–17, 1993, Jerusalem, Israel. Contemp. Math. 178, Amer. Math. Soc., Providence, RI, 71–89 (1994)
Bringmann, K., Ono, K., Wagner, I.: Eichler integrals of Eisenstein series as q-brackets of weighted t-hook functions on partitions. arXiv:2009.07236v1 [math.NT] (2020)
Comtet, L.: Advanced Combinatorics. The Art of Finite and Infinite Expansions. Enlarged edition, D. Reidel Publishing Co., Dordrecht (1974)
D’Arcais, F.: Développement en série. Intermédiaire Math. 20, 233–234 (1913)
Doman, B.: The Classical Orthogonal Polynomials. World Scientific, Singapore (2016)
Fulton, W.: Young Tableaux. Cambridge University Press, Cambridge (1997)
Han, G.: The Nekrasov-Okounkov hook length formula: refinement, elementary proof and applications. Ann. Inst. Fourier (Grenoble) 60(1), 1–29 (2010)
Heim, B., Neuhauser, M.: On conjectures regarding the Nekrasov-Okounkov hook length formula. Arch. Math. 113(4), 355–366 (2018)
Heim, B., Neuhauser, M.: Log-concavity of recursively defined polynomials. J. Integer Seq. 22, 12 (2019)
Heim, B., Neuhauser, M.: On the reciprocal of Klein’s absolute j-invariant and sign changes. Res. Number Theory 6(4), 1–8 (2020)
Heim, B., Neuhauser, M., Weisse, A.: Records on the vanishing of Fourier coefficients of powers of the Dedekind eta function. Res. Number Theory 4(3), 1–12 (2018)
Heim, B., Luca, F., Neuhauser, M.: Recurrence relations for polynomials obtained by arithmetic functions. Int. J. Number Theory 15(6), 1291–1303 (2019)
Heim, B., Neuhauser, M., Tröger, R.: Zeros of recursively defined polynomials. J. Differ. Equ. Appl. 26(4), 510–531 (2020)
Hong, L., Zhang, S.: Towards Heim and Neuhauser’s unimodality conjecture on the Nekrasov–Okounkov polynomials. arXiv:2008.10069 [math.CO]
Lehmer, D.: The vanishing of Ramanujan’s \(\tau (n)\). Duke Math. J. 14, 429–433 (1947)
Macdonald, I.G.: Symmetric Functions and Hall Polynomials, 2nd edn. Clarendon Press, Oxford (1995)
Nekrasov, N., Okounkov, A.: Seiberg–Witten theory and random partitions. arXiv:hep-th/0306238v2
Nekrasov, N., Okounkov, A.: Seiberg–Witten theory and random partitions. In: P. Etingof, V. Retakh, I. M. Singer (eds.) The unity of mathematics. In honor of the ninetieth birthday of I. M. Gelfand. Papers from the conference held in Cambridge, MA, USA, August 31–September 4, 2003. Progr. Math. 244 Birkhäuser Boston, 525–596 (2006)
Newman, M.: An identity for the coefficients of certain modular forms. J. Lond. Math. Soc. 30, 488–493 (1955)
Ono, K.: The Web of Modularity: Arithmetic of the Coefficients of Modular Forms and q-Series. American Mathematical Society, Providence (2004)
Serre, J.: Sur la lacunarité des puissances de \(\eta \). Glasgow Math. J. 27, 203–221 (1985)
Sibuya, M.: Log-concavity of Stirling numbers and unimodality of Stirling distributions. Ann. Inst. Stat. Math. 40(4), 693–714 (1988)
Westbury, B.: Universal characters from the Macdonald identities. Adv. Math. 202(1), 50–63 (2006)
Wilf, H.S.: The asymptotic behavior of the Stirling numbers of the first kind. J. Comb. Theory Ser. A 64(2), 344–349 (1993)
Authors' contributions
The authors thank the two anonymous referees for many helpful comments.
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Heim, B., Neuhauser, M. Horizontal and vertical log-concavity. Res. number theory 7, 18 (2021). https://doi.org/10.1007/s40993-021-00245-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s40993-021-00245-1