1 Introduction

Log-concavity of sequences of numbers, for example binomial coefficients and Stirling numbers, coefficients of polynomials, and values of discrete random variables, is an important characteristic studied in algebra, combinatorics, computer science, number theory, probability and statistical mechanics.

Comtet ([4], Chap. V), recorded horizontal and vertical recurrence relations for triangular sequences, including Stirling numbers of the first kind and of the second kind. This paper investigates horizontal and vertical log-concavity for the Pochhammer polynomials, D’Arcais and Nekrasov–Okounkov polynomials. In several cases the vertical log-concavity fails, but still a vertical C-log-concavity seems to be in place. We refer to a recent paper by Hong and Zhang ([15], see also Sect. 3).

In 2003, Nekrasov and Okounkov [18, 19] discovered a spectacular hook length formula, which comprises building blocks polynomials \(Q_n(x)\) of degree n involving all partitions \(\lambda \vdash n\) of n and the multisets of hook lengths \(\mathcal {H}(\lambda )\):

$$\begin{aligned} Q_n(x) := \sum _{ \lambda \vdash n} \prod _{ h \in \mathcal {H}(\lambda )} \left( \frac{h^2 + x}{h^2} \right) \in \mathbb {C}[x]. \end{aligned}$$

Shortly after that Westbury [24] and Han [8] also discovered the same formula utilizing different methods. The polynomials \(Q_n(x)\) have non-negative rational coefficients and the sequence of coefficients has no internal zeros. Applying Newton’s theorem could be considered in order to prove log-concavity, if the roots are real, which was conjectured (see Amdeberhan [1]). Recently, Heim and Neuhauser [9] disproved the conjecture. Nevertheless, there is overwhelming numerical evidence that \(Q_n(x)\) is still log-concave. We have used PARI/GP to check this up to \(n=1500\).

Recently, Hong and Zhang [15], supervised by Ono, invested in the log-concavity and unimodality of \(Q_n(x)\). They proved for sufficiently large n that a huge proportion of the coefficients of \(Q_n(x)\) at the beginning of the sequence have the log-concavity property, at the end they are decaying. Additionally, they came up with a conjecture which also implies the unimodality for \(Q_n(x)\) for large n.

In this paper we define families of polynomials \(\{P_n^{g,h}(x)\}_{n=1}^{\infty }\), where g and h are normalized non-vanishing arithmetic functions. Let \(P_0^{g,h}(x)=1\). Then

$$\begin{aligned} P_n^{g,h}(x) := \frac{x}{h(n)} \sum _{k=1}^n g(k) \, P_{n-k}^{g,h}(x). \end{aligned}$$
(1)

Although most of the results stated in this paper, assume that \(h \in \{ \mathop {\mathrm{id}},1\}\), we keep the general notation to emphasize the connection by (1) and the hope to come up with more general theorems in the future.

We are interested in particular in the arithmetic functions \( 1(n)=1\), \(\mathop {\mathrm{id}}(n)=n\), \(s(n)=n^2\) and \( \sigma (n)= \sum _{d \vert n} d \). Further, let \(\tilde{g}(n):= g(n)/n\). Note that \(\tilde{1}(n)= 1/n\). Suppose that \(G(T):=\sum _{n=1}^{\infty } g(n) T^n\) is analytic at \(T=0\). We will then have for \(h \in \{ \mathop {\mathrm{id}},1\}\) generating series of exponential and geometric type (see also Corollary 3):

$$\begin{aligned} \sum _{n=0}^{\infty } P_n^{g, \mathop {\mathrm{id}}}(x) \, T^n= & {} \exp \left( x \sum _{n=1}^{\infty } g(n) \, \frac{T^n}{n} \right) ,\end{aligned}$$
(2)
$$\begin{aligned} \sum _{n=0}^{\infty } P_n^{g,1}(x) \, T^n= & {} \frac{1}{ 1 - x \sum _{n=1}^{\infty } g(n) \, T^n}. \end{aligned}$$
(3)

We note that for specific arithmetic functions g, we obtain the Pochhammer polynomials (rising factorials: \(g=1\), \(h=\mathop {\mathrm{id}}\)), associated Laguerre polynomials (\(g=\mathop {\mathrm{id}}\), \(h=\mathop {\mathrm{id}}\)), Chebyshev polynomials of the second kind (\(g=\mathop {\mathrm{id}}\), \(h=1\)), and also polynomials attached to reciprocals of Klein’s j-invariant (\(g\left( n\right) \) is the \(n-1\)st coefficient of Klein’s j-invariant, cf. OEIS sequence A000521, divided by 744, \(h=1\)) and reciprocals of Eisenstein series \(E_k\) of weight k (\(g=\sigma _{k-1}\), \(h=1\)) [11, 13].

Important examples in this paper are the D’Arcais polynomials and the related Nekrasov–Okounkov polynomials. Let \(g(n)= \sigma (n)\) and \(h(n)=\mathop {\mathrm{id}}(n)=n\). Then the D’Arcais polynomials [5, 13, 24] \(P_n^{\sigma , \mathop {\mathrm{id}}}(x)\) are equal to the nth coefficient of the \(-x\)th power of the Dedekind \(\eta \)-function [21]. Nekrasov and Okounkov proved that

$$\begin{aligned} Q_n(x) = P_n^{\sigma , \mathop {\mathrm{id}}}(x +1). \end{aligned}$$

Brenti’s result [2], on polynomials with non-negative coefficients and where the sequence of coefficients has no internal zeros, implies that if the D’Arcais polynomials are log-concave then the Nekrasov–Okounkov polynomials also are log-concave. The converse of Brenti’s Theorem is in general not true and it is not generally true for unimodality.

The purpose of this paper is threefold. We first prove that there is a crossover between the coefficients of \(P_n^{\tilde{g},1}(x)\) and \(P_n^{g,\mathop {\mathrm{id}}}(x)\). The crossover transfers log-concavity from \(P_n^{\tilde{g},1}(x)\) to \(P_n^{g,\mathop {\mathrm{id}}}(x)\). Second, suppose that \(A_{n,m}^{g,h}\) is the mth coefficient of \(P_{n}^{g,h}(x)\). Suppose that m is fixed, then we examine the vertical log-concavity with respect to n. Hong and Zhang [15] defined a property which could still be true, when the vertical log-concavity fails. Let us name this new property vertical C-log-concavity (see Sect. 3). Finally we raise a question on horizontal and vertical C-log-concavity on the double sequence of coefficients of \(\{P_n^{g,h}(x)\}_{n=1}^{\infty }\), where \(h=1\) or \(h=\mathop {\mathrm{id}}\).

2 First results

Suppose that g is a normalized arithmetic function. We say that g is of moderate growth if G(T) is analytic at \(T=0\). Further, suppose that h is a normalized non-vanishing arithmetic function. We then have for \(n\ge 1\):

$$\begin{aligned} P_n^{g,h}(x) = A_{n,n}^{g,h} x^n + A_{n,n-1}^{g,h} x^{n-1}+ \ldots + A_{n,1}^{g,h} x. \end{aligned}$$

Here \(A_{n,n}^{g,h} = 1/\prod _{k=1}^n h(k)\) and \(A_{n,1}^{g,h}= g(n)/h(n)\). Moreover, suppose that the values of g and h are positive integers, then

$$\begin{aligned} \left( \prod _{k=1}^n h(k) \right) A_{n,m}^{g,h} \in \mathbb {N} \text { for } 1 \le m \le n . \end{aligned}$$
(4)

It is difficult to obtain results like (4) for arbitrary pairs (g, h). Since \(P_n^{\mathop {\mathrm{id}}, \mathop {\mathrm{id}}}\left( x\right) \) has only real roots, but some of the Nekrasov–Okounkov polynomials, e. g. \(Q_{10}(x) = P_{10}^{\sigma , \mathop {\mathrm{id}}} (x+1)\) have also non-real roots [9], it is obvious, that some results only work maybe for specifically chosen pairs. It is not clear to us if the following conversion principle can be stated in a more general form.

Theorem 1

(Conversion Principle) Suppose that g is a normalized arithmetic function of moderate growth. Then

$$\begin{aligned} A_{n,m}^{g,\mathop {\mathrm{id}}} = \frac{1}{m!} \, A_{n,m}^{\tilde{g},1}. \end{aligned}$$

Example 1

We have \(P_n^{1,1}(x) = x (x+1)^{n-1}\) for \(n\ge 1\). This implies that

$$\begin{aligned} A_{n,m}^{1,1} = \left( {\begin{array}{c}n-1\\ m-1\end{array}}\right) \text { and from Theorem 1 that } A_{n,m}^{\mathop {\mathrm{id}},\mathop {\mathrm{id}}} = \frac{1}{m!} \left( {\begin{array}{c}n-1\\ m-1\end{array}}\right) . \end{aligned}$$
(5)

This further implies that \(P_n^{\mathop {\mathrm{id}}, \mathop {\mathrm{id}}}(x) = \frac{x}{n} L_{n-1}^{(1)}\left( -x\right) \), where \(L_n^{(\alpha )}(x)\) is the associated Laguerre polynomial of degree n with parameter \(\alpha \) ([6], Chap. 3). Note that (5) gives conceptional proof of Theorem 2 in [10]; see also [13]. Recall that \(L_n^{(\alpha )}(x)\) for \(\alpha >-1\) are orthogonal polynomials and solutions of the differential equation

$$\begin{aligned} x \frac{ \mathrm {d}^2y}{\mathrm {d}x^2} + (\alpha + 1 -x) \frac{\mathrm {d}y}{\mathrm {d}x} + n y =0. \end{aligned}$$

Before we prove Theorem 1 we provide some applications.

Corollary 1

Suppose that \(P_n^{\tilde{g},1}(x)\) is log-concave, then \(P_n^{g,\mathop {\mathrm{id}}}\,(x)\) is log-concave.

We can also fix m and consider the sequence \(\{ A_{n,m}^{g,h}\}_n\). If this sequence is log-concave for all m we say that \(\{P_n^{g,h}(x)\}_n \) is vertically log-concave.

Corollary 2

\(\{ P_n^{\tilde{g},1}(x)\}_n \) is vertically log-concave iff \(\{P_n^{g,\mathop {\mathrm{id}}}\,(x)\}_n \) is vertically log-concave.

Proof of Theorem 1

We call \(\mathcal {E}_g(T):= \sum _{n=1}^{\infty } \frac{g(n)}{n} \, T^n\) the (modified) Eichler integral of G(T). In the case of \(g(n)= \sigma (n)\) and \(T= q := \text {e}^{2 \pi \text {i} \tau }\), where \(\tau \) is in the upper complex half-plane, \(\mathcal {E}_g(T)\) is the Eichler integral of \(\frac{1-E_2}{24}\) of the weight 2 quasi-modular Eisenstein series \(E_2(\tau )\). We refer to [3] for recent work on Eichler integrals.

We prove that for all \(m \in \mathbb {N}\):

$$\begin{aligned} \mathcal {E}_g(T)^m= & {} m! \,\, \sum _{n=m}^{\infty } A_{n,m}^{g, \mathop {\mathrm{id}}}\, T^n , \\ \mathcal {E}_g(T)^m= & {} \sum _{n=m}^{\infty } A_{n,m}^{\tilde{g}, 1} \, T^n . \end{aligned}$$

The strategy of the proof is the following. We consider the x expansion of \(\sum _{n=0}^{\infty } P_{n}^{g,h}(x)\, T^n\) for \(h \in \{\mathop {\mathrm{id}}, \, 1 \}\). In the domain of absolute convergence we interchange two infinite sums and compare the coefficients. The core of the proof is the transition from the exponential series to the geometric series. The formula utilizing the geometric series is given by

$$\begin{aligned} \sum _{n=0}^{\infty } P_{n}^{\tilde{g},1}(x)\, T^n = \frac{1}{1- x \, \mathcal {E}_g(T)}. \end{aligned}$$

This can be directly verified by comparing the Cauchy product of the two power series \(\sum _{n=0}^{\infty } P_{n}^{\tilde{g},1}(x)\, T^n \) and \(1- x \, \mathcal {E}_g(T)\) and the defining recursion formula of \(P_{n}^{\tilde{g},1}(x)\).

The formula utilizing the exponential series is given by

$$\begin{aligned} \sum _{n=0}^{\infty } P_{n}^{g, \mathop {\mathrm{id}}}(x)\, T^n = \exp \left( x \, \mathcal {E}_g(T) \right) . \end{aligned}$$

Suppose that the generating series \(\sum _{n=0}^{\infty } P_{n}^{g, \mathop {\mathrm{id}}}(x)\, T^n \) is denoted by \(F_g(x,T)\). First, we observe that the recursion formula (1) is encoded in the functional equation

$$\begin{aligned} \frac{\partial }{\partial T} F_g(x,T) = F_g(x,T) \, \frac{\mathrm {d}}{\mathrm {d}T}\left( x\mathcal {E}_{g}\left( T\right) \right) . \end{aligned}$$
(6)

Further, let \(f(n):= \sum _{d \vert n} \mu (d) \, g(n/d)\), where \(\mu \) is the Moebius function. Then it can be shown by a standard procedure (logarithmic differentiation), that the Euler product

$$\begin{aligned} \prod _{n=1}^{\infty } \left( 1 - T^n \right) ^{- \frac{x f(n)}{n}} \end{aligned}$$

satisfies the functional equation (6). Finally, since

$$\begin{aligned} \ln \prod _{n=1}^{\infty } \left( 1 - T^n \right) ^{- \frac{x f(n)}{n}} = \sum _{n,m=1}^{\infty } \frac{x \, f(n)}{n} \frac{T^{nm}}{m} = x \mathcal {E}_g(T), \end{aligned}$$

the proof has been completed. \(\square \)

From this proof we obtain the exponential and geometric realization of \(P_n^{g,h}(x)\).

Corollary 3

Let \(h=\mathop {\mathrm{id}}\) or \(h=1\), then we have identities (2) and (3) for the assigned generating series:

$$\begin{aligned} \sum _{n=0}^{\infty } P_n^{g, \mathop {\mathrm{id}}}(x) \, T^n= & {} \exp \left( x \sum _{n=1}^{\infty } g(n) \, \frac{T^n}{n} \right) ,\\ \sum _{n=0}^{\infty } P_n^{g,1}(x) \, T^n= & {} \frac{1}{ 1 - x \sum _{n=1}^{\infty } g(n) \, T^n}. \end{aligned}$$

3 Log-concavity and double sequences

Definition 1

Suppose that \(\left\{ a_n\right\} _{n=0}^{\infty }\) is a sequence of non-negative real numbers. A finite sequence is extended with zeros.

  1. (1)

    The sequence is called log-concave if \(a_n^2 \ge a_{n-1} \, a_{n+1}\) for \(n \ge 1\).

  2. (2)

    We denote a double sequence \(\mathcal {A}=\{a_{n,m}\}\) horizontally log-concave iff for every \(n_0 \in \mathbb {N}\) the sequence \(\{a_{n_0,m}\}\) is log-concave and vertically log-concave iff for every \(m_0 \in \mathbb {N}\) the sequence \(\{a_{n,m_0}\}\) is log-concave.

  3. (3)

    If for \(C>1\) fixed and for all \(m_0\) the sequence \(\{a_{n,m_0}\}_{1 \le n \le C^{m_0}}\) is log-concave, then we denote the double sequence \(\mathcal {A}\) as vertically C-log-concave.

We are mainly interested in double sequences \(\mathcal {A}=\{a_{n,m}\}\) of triangular shape: \(a_{n,m}=0\) for \(m>n\) or \(m=0\), and \(a_{n,m}\) are otherwise positive.

Suppose that g and h are normalized arithmetic functions with positive real values. Suppose that g is of moderate growth. Then we assign to the family of polynomials \(P_n^{g,h}(x)\) the double sequence \(\mathcal {A}^{g,h}=\{a_{n,m}^{g,h}\}\) of triangular shape by putting

$$\begin{aligned} a_{n,m}^{g,h} = A_{n,m}^{g,h} \quad \text { for } 1 \le m \le n, \end{aligned}$$

and otherwise zero. If \(\mathcal {A}^{g,h}\) is horizontally or vertically log-concave or vertically C-log-concave we give \(P_n^{g,h}(x)\) the same label. We are interested in the D’Arcais polynomials \(P_n^{\sigma , \mathop {\mathrm{id}}}(x)\) which are conjectured to be horizontally log-concave. In the next section we provide counter-examples for vertical log-concavity and put this observation in the context of a conjecture by Hong and Zhang [15], addressing the vertical C-log-concavity.

Let us first give some examples, which may serve as a source of ideas to prove the Hong and Zhang conjecture. Example 1 leads to:

Proposition 1

Let \(g(n)=h(n)\) equal to 1(n) or \(\mathop {\mathrm{id}}\left( n\right) \). Then the assigned double sequences \(\mathcal {A}^{1,1}\) and \(\mathcal {A}^{\mathop {\mathrm{id}}, \mathop {\mathrm{id}}}\) are horizontally and vertically log-concave.

Proof

We recall that

$$\begin{aligned} a_{n,m}^{1,1} = \left( {\begin{array}{c}n-1\\ m-1\end{array}}\right) . \end{aligned}$$

Then \(\mathcal {A}^{1,1}\) consists of binomial coefficients, and therefore are (horizontally) log-concave. Binomial coefficients are also vertically log-concave:

$$\begin{aligned} {\left( {\begin{array}{c}n\\ k\end{array}}\right) }^2 \ge \left( {\begin{array}{c}n+1\\ k\end{array}}\right) \, \left( {\begin{array}{c}n-1\\ k\end{array}}\right) . \end{aligned}$$

Horizontal and vertical log-concavity of \(\mathcal {A}^{1,1}\) implies by Corollary 1 and Corollary 2 the proof of the proposition. This could also be obtained by a direct calculation. \(\square \)

Example 2

Let \(s\left( n\right) =n^2\). We recall from [10] that

$$\begin{aligned} A_{n,m}^{s, \mathop {\mathrm{id}}} = \frac{1}{m!} \left( {\begin{array}{c}n+m-1\\ 2m-1\end{array}}\right) .\end{aligned}$$

We obtain:

Proposition 2

The double sequences \(\mathcal {A}^{\mathop {\mathrm{id}},1}\) and \(\mathcal {A}^{s, \mathop {\mathrm{id}}}\) are horizontally and vertically log-concave.

Proof

It is sufficient to show that the double sequence \(\{ \left( {\begin{array}{c}n+m-1\\ 2m-1\end{array}}\right) \}_{n,m}\) is horizontally and vertically log-concave. This is shown in a straightforward manner.\(\square \)

Example 3

The polynomials \(n! \, P_n^{1,\mathop {\mathrm{id}}}(x)\) are obtained by the raising factorials. We have

$$\begin{aligned} P_n^{1, \mathop {\mathrm{id}}}(x) = \frac{ x (x+1) \ldots (x+n-1)}{n!}. \end{aligned}$$

Suppose that \(S\left( n,m \right) = \left[ \begin{array}{c} n \\ m \end{array} \right] \) is the unsigned Stirling number of the first kind and \({\widetilde{1}}(n) = \frac{1}{n}\). Then

$$\begin{aligned} A_{n,m}^{1, \mathop {\mathrm{id}}} = \frac{1}{n!} \left[ \begin{array}{c} n \\ m \end{array} \right] \text { and } A_{n,m}^{{\widetilde{1}}, 1} = \frac{m!}{n!} \left[ \begin{array}{c} n \\ m \end{array} \right] . \end{aligned}$$

Recall that the unsigned Stirling numbers of the first kind satisfy a three term recursion formula, similar to the recursion formula of binomial coefficients:

$$\begin{aligned} S(n,m) = (n-1) S(n-1,m) + S(n-1,m-1). \end{aligned}$$

This example is quite interesting. As a first result we have:

Proposition 3

The double sequences \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) and \(\mathcal {A}^{\tilde{1}, 1}\) are horizontally log-concave but not vertically log-concave.

Proof

The double sequence \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) is horizontally log-concave according to the theorem by Newton. To prove that the double sequence \(\mathcal {A}^{\tilde{{1}}, 1}\) is horizontally log-concave we cannot apply Newton’s theorem, since we do not know if \(P_n^{\tilde{{1}},1}(x)\) has only real roots. \(\mathcal {A}^{\tilde{{1}}, 1}\) is horizontally log-concave iff

$$\begin{aligned} m S(n,m)^2 \ge (m+1) \,S(n,m+1) \, S(n,m-1). \end{aligned}$$
(7)

Since \(S\left( n,m\right) =0\) only for \(m\le 0\) or \(m\ge n+1\), the Eq. (7) is true for \(m\le 1\) and \(m\ge n\).

For the rest of this part of the proof we now assume \(2\le m\le n-1\), which implies that all in (7) involved Stirling numbers are non-zero. From this we obtain

$$\begin{aligned} mS\left( n,m\right) /S\left( n,m-1\right) \ge \left( m+1\right) S\left( n,m+1\right) /S\left( n,m\right) . \end{aligned}$$
(8)

Sibuya ([23], Corollary 3.1) has shown that (8) holds strictly which proves our claim.

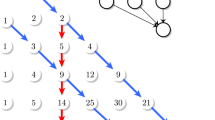
To disprove the vertical log-concavity, we record the coefficients of the first six polynomials \(P_n^{1, \mathop {\mathrm{id}}}(x)\).

\(n! \, {A}_{n,m}^{1, \mathop {\mathrm{id}}}\)

\(m=6\)

\(m=5\)

\(m=4\)

\(m=3\)

\(m=2\)

\(m=1\)

\(n=6\)

1

15

85

225

274

120

\(n=5\)

0

1

10

35

50

24

\(n=4\)

0

0

1

6

11

6

\(n=3\)

0

0

0

1

3

2

\(n=2\)

0

0

0

0

1

1

\(n=1\)

0

0

0

0

0

1

Let \(m=1\), then \(n_0=2\) is the smallest n, such that

$$\begin{aligned} \left( A_{n,1}^{\tilde{{1}}, 1}\right) ^2 \ge A_{n+1,1}^{\tilde{{1}}, 1} \,\, A_{n-1,1}^{\tilde{{1}}, 1}. \end{aligned}$$
(9)

fails. Moreover, (9) fails for all \(n \ge 2\).

Let \(m=2\), then \(n=n_0=5\) is the smallest n, such that

$$\begin{aligned} \left( A_{n,2}^{{\tilde{1}}, 1}\right) ^2 \ge A_{n+1,2}^{\tilde{{1}}, 1} \,\, A_{n-1,2}^{\tilde{{1}}, 1}. \end{aligned}$$
(10)

fails.\(\square \)

Remark

From ([14], Example 2.3) we obtain \(P_{n+1}^{1,\mathop {\mathrm{id}}}\left( x\right) =\frac{n+x}{n+1}P_{n}^{1,\mathop {\mathrm{id}}}\left( x\right) \). There is no obvious finite recursion formula for \(P_{n}^{\tilde{{1}},1}\left( x\right) \).

In the following we show that also in the case of \(m=2\) the inequality (10) fails for all \(n \ge n_0=5\). Let \(H(n)=\sum _{k=1}^n \frac{1}{k}\) denote the nth harmonic number. The sequence of harmonic numbers is log-concave. It is easy to see that

$$\begin{aligned} S(n,1)= (n-1)! \text { and } S(n,2) = (n-1)! \,\, H(n-1). \end{aligned}$$

Thus, \(A_{n,2}^{\tilde{{1}}, 1} = \frac{2}{n} \, H(n-1)\). We study the function

$$\begin{aligned}\Delta (n):= (n^2-1) H(n-1)^2 - n^2 H(n) H(n-2).\end{aligned}$$

Since \(H(n)= H(n-1) + \frac{1}{n}\), we obtain:

$$\begin{aligned} \Delta (n) = \frac{n}{n-1} ( H(n-1)+ 1) - H(n-1)^2. \end{aligned}$$

Let \( n \ge 2\). We have for \(2\le n\le 4\) the bounds \(1\le H\left( n-1\right) <2\). Thus,

$$\begin{aligned} \Delta \left( n\right)\ge & {} \frac{4}{3}\left( H\left( n-1\right) +1\right) -\left( H\left( n-1\right) \right) ^{2}\\= & {} \frac{1}{3}\left( 2+3H\left( n-1\right) \right) \left( 2-H\left( n-1\right) \right) >0. \end{aligned}$$

Otherwise, \(H(n-1) >2\), which leads to

$$\begin{aligned} \Delta \left( n\right)\le & {} \frac{4}{3}\left( H\left( n-1\right) +1\right) -\left( H\left( n-1\right) \right) ^{2}\\= & {} \frac{1}{3}\left( 2+3H\left( n-1\right) \right) \left( 2-H\left( n-1\right) \right) <0. \end{aligned}$$

4 On Hong and Zhang’s conjecture

Recently, Hong and Zhang [15] presented an interesting conjecture which implies that the Nekrasov–Okounkov polynomials are unimodal for large n.

4.1 Nekrasov–Okounkov polynomials

In 2003 Nekrasov and Okounkov, in an arXiv preprint ([18], formula (6.12)), announced a remarkable new type of hook length formula, based on their work on random partitions and the Seiberg–Witten theory (final publication [19]). Shortly after their discovery, Westbury [24] and Han [8] also spotted the hook length formula in connection with the Macdonald identities. Westbury utilized properties of twisted universal characters and Han properties of t-cores.

The hook length formula relates the sum over products of partition hook lengths [7, 17] to the coefficients of complex powers of Euler products [12, 20, 22], which is essentially a power of the Dedekind eta function.

Suppose that \(\lambda \) is a partition of n denoted by \(\lambda \vdash n\) with weight \(|\lambda |=n\). We denote by \(\mathcal {H}(\lambda )\) the multiset of hook lengths associated to \(\lambda \) and by \(\mathcal {P}\) the set of all partitions. The Nekrasov–Okounkov hook length formula is given by

$$\begin{aligned} \sum _{ \lambda \in \mathcal {P}} q^{|\lambda |} \prod _{ h \in \mathcal {H}(\lambda )} \left( 1 - \frac{z}{h^2} \right) = \prod _{m=1}^{\infty } \left( 1 - q^m \right) ^{z-1}. \end{aligned}$$
(11)

The identity (11) is valid for all \(z \in \mathbb {C}\). The Dedekind eta function \(\eta (\tau )\) is given by \(q^{\frac{1}{24}} \prod _{m=1}^{\infty } \left( 1 - q^m \right) \) (see [21]). In [9] we revised and refined three conjectures posted by Amdeberhan [1]. The formula (11) is built up of a family of polynomials \(Q_n(x)\). The nth Nekrasov–Okounkov polynomial is given by

$$\begin{aligned} Q_n(x) := \sum _{ \lambda \vdash n} \prod _{ h \in \mathcal {H}(\lambda )} \left( \frac{h^2 + x}{h^2} \right) \in \mathbb {C}[x]. \end{aligned}$$
(12)

Note that all the coefficients of \(Q_n(x)\) are non-negative. Suppose that \(Q_n(x)\) has only real roots (previous Conjecture 2), then we know already from Newton that this implies that \(Q_n(x)\) is log-concave, and hence unimodal (previous Conjecture 3). We disproved Conjecture 2, and used PARI/GP to check that \(Q_n(x)\) is log-concave for \(n \le 1500\). Note that the roots of \(Q_n(x)\) are directly related to the Lehmer conjecture [12, 16].

4.2 D’Arcais polynomials

In 1913 D’Arcais [5] studied a sequence of polynomials \(P_n(x)\) (which are denoted D’Arcais polynomials [24]):

$$\begin{aligned} \sum _{n=0}^{\infty } P_{n}\left( x\right) \, q^{n} = \prod _{n=1 }^{\infty } \left( 1 - q^n \right) ^{-x}. \end{aligned}$$

The coefficients are called D’Arcais numbers [4]. Newman and Serre [20, 22] studied the polynomials in the context of modular forms. Serre proved his famous theorem on lacunary modular forms, utilizing the factorization of \(P_n(x)\) for \( 1 \le n \le 10\) over \(\mathbb {Q}\).

4.3 Hong and Zhang’s conjecture

Hong and Zhang [15] investigated a conjecture, published by Heim and Neuhauser [9] on the unimodality of the Nekrasov–Okounkov polynomials and the related log-concavity (see also [1]).

We consider the generating series

$$\begin{aligned}f(q):= \sum _{n=1}^{\infty } \tilde{\sigma }(n) \, q^n = \sum _{n=1}^{\infty } \sigma (n) \, \frac{q^n}{n}.\end{aligned}$$

Let \(m \in \mathbb {N}\). We denote by \(b_{m,n}\) the coefficients of the q-expansion of the mth power of f(q) and we put otherwise \(b_{m,n}=0\). We follow [15] with \(m=k\) and \(b_{m,n}= c_{n,k}\).

Conjecture

(Hong, Zhang) There exists a constant \(C>1\), such that for all \(m \ge 2\) and \(1 \le n \le C^m\):

$$\begin{aligned} b_{m,n}^2 \ge b_{m,n-1} \, b_{m,n+1}. \end{aligned}$$

At the end of their paper they offer evidence and also remark that it is very likely that \(C=2\) may fulfill their conjecture. Finally, they prove that the validity of their conjecture implies that the Nekrasov–Okounkov polynomials are unimodal for large degrees.

4.4 Vertical version of the Hong–Zhang conjecture

The following identity puts the numbers \(b_{m,n}\) in the context of double sequences derived by polynomials defined by the recursion (1). We consider the q-expansion of reciprocal power series [11], induced by normalized arithmetic functions g, which provides the link to the polynomials \(P_n^{g,1}(x)\):

$$\begin{aligned} \frac{1}{1 - x \sum _{n=1}^{\infty } g(n) \, q^n} = \sum _{n=0}^{\infty } P_n^{g, 1}(x) \, q^n. \end{aligned}$$

Thus, the numbers \(b_{m,n}\) are the mth coefficients of the polynomial \(P_n^{\tilde{\sigma }, 1} (x)\). The duality property shows that \(b_{m,n}/m!\) is also equal to the mth coefficients \(A_{n,m}\) of the D’Arcais polynomials. Hence, we immediately obtain:

Theorem 2

Let \(C>1\). The Hong–Zhang conjecture with \(C>1\) is true iff the double sequence \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) attached to the D’Arcais polynomials is vertically C-log-concave iff the double sequence \(\mathcal {A}^{\widetilde{\sigma }, 1}\) is vertically C-log-concave.

5 Open challenges and further study

Suppose that g is a normalized positive real-valued arithmetic function of moderate growth. We consider double sequences \(\mathcal {A}^{g,h}\) assigned to families of polynomials \(P_n^{g,\mathop {\mathrm{id}}}(x)\) and \(P_n^{g,1}(x)\) for \(h=\mathop {\mathrm{id}}\) or \(h=1\). The horizontal and vertical log-concavity of sequences are important characteristics. We utilize a conversion principle, Theorem 1, which provides an explicit translation from the double sequences \(\mathcal {A}^{g, \mathop {\mathrm{id}} }\) to the double sequence \(\mathcal {A}^{\tilde{g},1}\).

5.1 Unsigned Stirling numbers of the first kind

Let \(g=1\) and \(h={\mathop {\mathrm{id}}}\). Then the double sequence \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) assigned to

$$\begin{aligned} P_n^{1,\mathop {\mathrm{id}}}(x) = \frac{1}{n!} \prod _{k=0}^n (x +k) = \frac{1}{n!} \sum _{m=1}^{n} S(n,m) \, x^m \end{aligned}$$

is horizontal log-concave. We have already shown that the vertical log-concavity fails. Nevertheless, numerical investigation shows similarities to the Hong–Zhang conjecture. We have recorded this in the following Table 1.

Table 1 Smallest integers \(n=n_{0}\) where \(\left( \frac{S\left( n,m\right) }{n!}\right) ^{2}<\frac{S\left( n-1,m\right) S\left( n+1,m\right) }{\left( n-1\right) !\left( n+1\right) !}\).
Full size table

Proposition 4

For large n the sequence \(\frac{S\left( n,m\right) }{n!}\) is not log-concave.

In the proof we will use Landau’s big O notation for functions on an unbounded subset of the positive real numbers and \(f\left( x\right) =O\left( g\left( x\right) \right) \) if there is a \(C>0\) and an \(x_{0}\) such that \(\left| f\left( x\right) \right| \le Cg\left( x\right) \) for all \(x\ge x_{0}\). We also will need the polynomials \(v_{m}\left( y\right) \) of degree m defined by the power series expansion of \(\frac{\text {e}^{xy}}{x\Gamma \left( x\right) }=\sum _{m=0}^{\infty }v_{m}\left( y\right) x^{m}\).

Proof

From [25] we can deduce that \(\frac{S\left( n,m\right) }{n!}=\frac{v_{m-1}\left( \ln \left( n-1\right) \right) }{n}+O\left( n^{\varepsilon /2-2}\right) \) for any \(0<\varepsilon <1\). Then

$$\begin{aligned}&\left( \frac{S\left( n,m\right) }{n!}\right) ^{2}-\frac{S\left( n-1,m\right) S\left( n+1,m\right) }{\left( n-1\right) ! \left( n+1\right) !}\\&\quad =\left( \frac{v_{m-1}\left( \ln \left( n-1\right) \right) }{n}\right) ^{2}-\frac{v_{m-1}\left( \ln \left( n-2\right) \right) }{n-1}\frac{v_{m-1}\left( \ln \left( n\right) \right) }{n+1}+O\left( n^{\varepsilon -3}\right) . \end{aligned}$$

Now \(\ln \left( n-1\pm 1\right) =\ln \left( n-1\right) +\ln \left( 1\pm \frac{1}{n-1}\right) =\ln \left( n-1\right) +O\left( n^{-1}\right) \). Since \(v_{m-1}\left( y\right) \) is a polynomial we have \(v_{m-1}\left( \ln \left( n-1\pm 1\right) \right) =v_{m-1}\left( \ln \left( n-1\right) \right) +O\left( n^{-1}\right) \). Together this yields

$$\begin{aligned}&\left( \frac{S\left( n,m\right) }{n!}\right) ^{2}-\frac{S\left( n-1,m\right) S\left( n+1,m\right) }{\left( n-1\right) !\left( n+1\right) !}\\&\quad =\left( \frac{1}{n^{2}}-\frac{1}{n^{2}-1}\right) \left( v_{m-1}\left( \ln \left( n-1\right) \right) \right) ^{2}+O\left( n^{\varepsilon -3}\right) . \end{aligned}$$

Therefore its sign is determined by the sign of

$$\begin{aligned} \left( \frac{1}{n^{2}}-\frac{1}{n^{2}-1}\right) \left( v_{m-1}\left( \ln \left( n-1\right) \right) \right) ^{2}<0. \end{aligned}$$

\(\square \)

Challenge 1

Is the double sequence \(\mathcal {A}^{1, \mathop {\mathrm{id}}}\) vertically C-log-concave?

We expect that the answer to this question will also give some insight in the Hong–Zhang conjecture.

5.2 D’Arcais polynomial version of Hong–Zhang’s conjecture

Hong and Zhang [15] considered the coefficients \(b_{m,n}\) of the mth power of the generating series

$$\begin{aligned}f(q)= \sum _{n=1}^{\infty } \sigma (n) \, \frac{q^n}{n}\end{aligned}$$

and conjectured that there exists a \(C>1\), such that for \(m \ge 2\) and \(1 \le n \le C^m\):

$$\begin{aligned} b_{m,n}^2 \ge b_{m,n-1} \, b_{m,n+1}. \end{aligned}$$

We have proven in this paper that the conjecture is equivalent to the vertical C-log-concavity of the D’Arcais polynomials \(P_n^{\sigma , \mathop {\mathrm{id}}}(x)\) given by

$$\begin{aligned} \sum _{n=0}^{\infty } P_n^{\sigma , \mathop {\mathrm{id}}}\left( x\right) \, q^n = \prod _{n=1}^{\infty } \left( 1 - q^n \right) ^{-x}. \end{aligned}$$

Challenge 2

Assume \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) horizontally log-concave. Does this imply the Hong–Zhang conjecture?

5.3 D’Arcais polynomials

The Nekrasov–Okounkov \(Q_n(x)\) polynomials are shifted D’Arcais polynomials. We have checked numerically that for \(n \le 1500\) the D’Arcais polynomials are (horizontally) log-concave. We would reinforce the conjecture stated in [1] and [9] on the unimodality of the Nekrasov–Okounkov polynomials.

Challenge 3

(Conjecture) The double sequence \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) assigned to the D’Arcais polynomials is horizontally log-concave.

By Brenti’s result this implies the log-concavity of the Nekrasov–Okounkov polynomials and therefore also the unimodality.

5.4 Examples for horizontal and vertical C-log-concavity

To get a better understanding of the D’Arcais polynomials it would be beneficial to know which property of the input function \(g=\sigma \) enforces the horizontal and vertical properties of the double sequences \(\mathcal {A}^{\sigma , \mathop {\mathrm{id}}}\) and \(\mathcal {A}^{\tilde{\sigma }, \mathop {\mathrm{1}}}\).

Challenge 4

Characterize the set of normalized positive-valued arithmetic functions, which provide horizontally and vertically (C-)log-concave properties of the assigned double sequences.