Understanding the Short Run Relationship Between Stock Market and Growth in Emerging Economies

Abstract

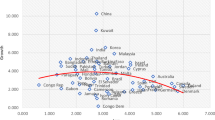
Contemporaneous correlation coefficients between per capita growth and market capitalization to GDP ratio calculated for 35 countries reveal highest correlations for emerging economies. The paper explains this phenomenon in an extended Lucas (Econmetrica 46(6):1429–1445, 1978) asset pricing model with production, accumulation and growth with two separately added additional features, international borrowing by domestic firms and holding of domestic shares by foreign agents. It is shown that in the first scenario, growth enhancing productivity shock increases market capitalization ratio in the short run and in the second, a positive demand shock increases short run growth. The model is calibrated using quarterly Indian data.

Appendices

A Household’s Optimization Conditions

The objective function of the household can be written as

$$\begin{aligned}&Max:E_{0}\sum _{t=0}^{\infty }\beta ^{t}u(c_{t}) \end{aligned}$$

(34)

$$\begin{aligned}&s.t.:\int _{0}^{1}p_{t}^{z}(i)\left( z_{t+1}(i)-z_{t}(i)\right) di+c_{t}=\int _{0}^{1}d_{t}(i)z_{t}(i)di \end{aligned}$$

(35)

as in (5) and (6).

The Lagrange function is formed as:

$$\begin{aligned} N_{t}= & {} \sum _{t=0}^{\infty }\beta ^{t}u(c_{t})+\omega _{t}\left[ \int _{0}^{1}d_{t}(i)z_{t}(i)di-\int _{0}^{1}p_{t}^{z}(i)\left[ z_{t+1}(i)-z_{t}(i)\right] -c_{t}\right] \nonumber \\&+\omega _{t+1}\left[ \int _{0}^{1}d_{t+1}(i)z_{t+1}(i)di \right. \nonumber \\&\left. -\int _{0}^{1}p_{t+1}^{z}(i)\left[ z_{t+2}(i)-z_{t+1}(i)\right] di-c_{t+1}\right] \end{aligned}$$

(36)

where $\omega _{t}$ is the Lagrange Multiplier for period t.

Since households and firms are all identical, the i subscript can be ignored. Choice variables for the household are $c_{t}$ and $z_{t+1}$.

First Order Condition with respect to $c_{t}$ gives

$$\begin{aligned} \omega _{t}=\beta ^{t}u'(c_{t}) \end{aligned}$$

(37)

First Order Condition with respect to $z_{t+1}$ gives

$$\begin{aligned} \omega _{t}p_{t}^{z}=\omega _{t+1}[d_{t+1}+p_{t+1}^{z}] \end{aligned}$$

(38)

Combining the two First Order Conditions I get

$$\begin{aligned} u^{\prime }(c_{t})p_{t}^{z}=\beta E_{t}u^{\prime }(c_{t+1})\left( d_{t+1}+p_{t+1}^{z}\right) \end{aligned}$$

(39)

which is Eq. (8) in Section 2.

B Expression for Asset Price

In equilibrium,

$$\begin{aligned} c_{t}=d_{t} \end{aligned}$$

This is in line with Lucas (1978). Taking into account this assumption as well as the assumption of a logarithmic utility function, i.e. $u(c_{t})=\ln c_{t}$, the stock Euler equation in (8) becomes

$$\begin{aligned} \frac{p_{t}^{z}}{c_{t}}= & {} \beta E_{t}\left( \frac{c_{t+1}+p_{t+1}^{z}}{ c_{t+1}}\right) \end{aligned}$$

(40)

$$\begin{aligned}= & {} \beta \left[ 1+E_{t}\left( \frac{p_{t+1}^{z}}{c_{t+1}}\right) \right] \nonumber \\= & {} \beta \left[ 1+\beta \left\{ 1+E_{t}\left( \frac{p_{t+2}^{z}}{c_{t+2}} \right) \right\} \right] \nonumber \\= & {} \beta \left[ 1+\beta +\beta ^{2}+\cdots +E_{t}\left\{ \lim _{n\rightarrow \infty }\beta ^{n-1}\left( \frac{p_{t+n}^{z}}{c_{t+n}}\right) \right\} \right] \nonumber \\= & {} \frac{\beta }{1-\beta }+\beta E_{t}\left\{ \lim _{n\rightarrow \infty }\beta ^{n-1}\left( \frac{p_{t+n}^{z}}{c_{t+n}}\right) \right\} \end{aligned}$$

(41)

If the asset price is bounded (i.e. it cannot go to a value such that it would cost more than the household’s total income to buy a single asset), it is straight forward to see that the limit term in Eq. (8) goes to zero. This means that the equilibrium asset price becomes

$$\begin{aligned} p_{t}^{z}=\frac{\beta }{1-\beta }c_{t} \end{aligned}$$

(42)

Market Capitalization Ratio and Per Capita Growth with Borrowing

In the borrowing constrained model, the maximization problem of the firm can be expressed formally as in Eqs. (24) and (25).

In order to solve the above maximization problem, I set up the Lagrange function as in Eq. (26).

At time t, the choice variables of the firm are its investment $k_{t+1}$ and the amount it decides to borrow i.e. $b_{t}$.

The first order conditions to the Lagrangian problem with respect to $k_{t+1}$ and $b_{t}$ implies

$$\begin{aligned} \frac{\lambda _{t}}{r^{\prime }}-1+m_{t,t+1}\left[ \epsilon _{t+1}+\left( 1-\delta \right) \right] =0 \end{aligned}$$

and

$$\begin{aligned} 1-\lambda _{t}-E_{t}m_{t,t+1}r^{\prime }=0 \end{aligned}$$

respectively.

Combining these first order conditions by equating $\lambda _{t}$, I have

$$\begin{aligned}&E_{t}m_{t,t+1}\left[ {\epsilon _{t+1}-\delta }\right] =\left[ 1-\frac{1}{r^{\prime }}\right] \\&\frac{1}{c_{t}}\left[ 1-\frac{1}{r^{\prime }}\right] =\beta E_{t}{c_{t+1}}\left[ \epsilon _{t+1}-\delta \right] \end{aligned}$$

From the equilibrium resource constraint

$$\begin{aligned} \epsilon _{t}k_{t}+b_{t}=c_{t}+\left[ k_{t+1}-(1-\delta )k_{t}\right] +r^{\prime }b_{t-1} \end{aligned}$$

(43)

In the borrowing constrained equilibrium, where $b_{t}=\frac{k_{t+1}}{ r^{\prime }}$, this resource constraint becomes

$$\begin{aligned} c_{t}+k_{t+1}\left[ 1-\frac{1}{r^{\prime }}\right] =k_{t} \left[ {\epsilon _{t}-\delta } \right] \end{aligned}$$

which can be expressed as

$$\begin{aligned} {\epsilon _{t+1}-\delta }= \frac{c_{t+1}+k_{t+2}\left[ 1-\frac{1}{r^{\prime }} \right] }{k_{t}} \end{aligned}$$

(44)

Using the above relationship from (44) in the equilibrium resource constraint in (43), I have

$$\begin{aligned}&\left. \frac{k_{t+1}}{c_{t}}-\frac{1}{r^{\prime }}\right) =\beta E_{t}\left. \left( 1+\frac{k_{t+2}}{c_{t+1}}- \frac{1}{r^{\prime }}\right) \right) \nonumber \\&\frac{k_{t+1}}{c_{t}}=\frac{\beta }{1-\beta }\left( \frac{1}{ r^{\prime }-1}\right) \end{aligned}$$

(45)

Plugging in the relation from (45) in the equilibrium resource constraint in (43),the borrowing constrained equilibrium consumption $c_{t}$ and capital accumulation $k_{t+1}$ can be solved as

$$\begin{aligned} c_{t}=\left( 1-\beta \right) \left( {\epsilon _{t}- -\delta }{\psi _{t}}\right) k_{t} \end{aligned}$$

and

$$\begin{aligned} k_{t+1}=\beta \left( \frac{r^{\prime }}{r^{\prime }-1}\right) \left( \epsilon _{t}-\delta \right) k_{t} \end{aligned}$$

The equilibrium market capitalization ratio is given by

$$\begin{aligned} mk_{t}=\frac{p_{t}^{z}}{y_{t}}=\left( \frac{\beta }{1-\beta }\right) \frac{ c_{t}}{y_{t}}=\frac{p_{t}^{z}}{y_{t}}=\beta \left( 1 - \frac{\delta }{\epsilon _t}\right) \end{aligned}$$

which is (23) and the equilibrium output growth is given by

$$\begin{aligned} yg_{t}=\frac{\epsilon _{t}k_{t}}{\epsilon _{t-1}k_{t-1}}=\beta \left( \frac{\epsilon _{t}}{\epsilon _{t-1}}\right) \left( \frac{r^{\prime }}{r^{\prime }-1}\right) \left( \epsilon _{t-1}-\delta \right) \end{aligned}$$

which is (24).