G-birational superrigidity of Del Pezzo surfaces of degree 2 and 3

Abstract

Any minimal Del Pezzo G-surface S of degree smaller than 3 is G-birationally rigid. We classify those which are G-birationally superrigid, and for those which fail to be so, we describe the equations of a set of generators for the infinite group $\mathrm{Bir}^G(S)$ of G-birational automorphisms.

1 Introduction

The group of birational automorphisms of $\mathbb {P}^2(\mathbb {C})$ is classically known as Cremona group, denoted $\mathrm{Cr}_2(\mathbb {C})$. The classification of its finite subgroups up to conjugacy rose the interest of many classical authors and it has been completed in [5]. In this paper, we refine the description of the conjugacy class of some special finite subgroups.

The key reduction step in the classification consists in associating to any finite subgroup G of $\mathrm{Cr}_2(\mathbb {C})$ a group of automorphisms of a rational surface, isomorphic to G, see [5, Section 3.4]. Via a G-equivariant version of Mori theory, one can suppose that the surface is minimal with respect to the G-action. Here, we concentrate our attention to those finite subgroups of $\mathrm{Cr}_2(\mathbb {C})$ which act minimally by automorphisms on Del Pezzo surfaces S of degree 2 and 3. In particular, when the normaliser of G is not generated by automorphisms of the Del Pezzo surface, i.e., the surface S is not G-birationally superrigid, we describe explicitly the generators of the normaliser.

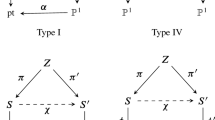
In order to formulate our main results, we recall the definition of minimal G-surface. Let $(S, \rho )$ be a G-surface, i.e., a nonsingular surface S defined over $\mathbb {C}$, endowed with the action of a finite group of automorphisms $\rho :G \rightarrow \mathrm{Aut}(S)$. Given two G-surfaces $(S, \rho )$ and , we say that a rational map $\varphi :S \dashrightarrow S'$ is G-rational if for any $g \in G$ the following diagram commutes:

for some . Then, a minimal G-surfaceS is a G-surface with the property that any G-birational morphism $S \rightarrow S'$ is an isomorphism. Equivalently, it is the output of a G-equivariant minimal model program, and as in the non-equivariant case, if S is rational, it is either a Del Pezzo surface with $\mathrm{Pic}^G(S)\simeq \mathbb {Z}$, i.e., $-K_S$ is ample, or a conic bundle with $\mathrm{Pic}^G(S)\simeq \mathbb {Z}^2$ (cf. [5, Theorem 3.8]).

The main properties investigated in this paper are described in the following definitions.

Definition 1.1

Let $(S, \rho )$ be a minimal Del Pezzo G-surface. Then $(S, \rho )$ is G-birationally rigid if there is no G-birational map from S to any other minimal G-surface. Equivalently, if $S'$ is any minimal G-surface and $\varphi :S \dashrightarrow S'$ is any G-birational map, then S is G-isomorphic to $S'$, not necessarily via $\varphi$. More precisely, there exists a G-birational automorphism $\sigma :S \dashrightarrow S$ such that is a G-biregular map.

Definition 1.2

The minimal Del Pezzo G-surface $(S, \rho )$ is G-birationally superrigid if it is G-birationally rigid and in addition, in the notation of Definition 1.1, any G-birational map $\varphi :S \dashrightarrow S'$ is biregular. In particular, the group of G-biregular automorphisms coincides with the group of G-birational automorphisms, i.e., $\mathrm{Aut}^G(S)=\mathrm{Bir}^G(S)$.

A classical theorem by Segre [9] and Manin [8] establishes that nonsingular cubic surfaces of Picard number 1 defined over a non-algebraically closed field are birationally rigid. In analogy with this arithmetic case, Dolgachev and Iskoviskikh showed in [5, Section 7.3] that minimal Del Pezzo G-surfaces of degree smaller than 3 are G-birationally rigid. In this paper we determine which minimal Del Pezzo G-surfaces of degree 2 and 3 are G-birationally superrigid. When the G-surface is not G-birationally superrigid, we describe the generators of the group of G-birational automorphisms $\mathrm{Bir}^G(S)$, or equivalently the normaliser of the corresponding subgroup G in $\mathrm{Cr}_2(\mathbb {C})$. Here, we collect our main results, adopting the notation of [5]:

Theorem 1.3

Let G be a non-cyclic group and S be a minimal Del Pezzo G-surface of degree 3. Then S is G-birationally superrigid, unless G is isomorphic to the symmetric group $S_3$ and S is not the Fermat cubic surface.

In this case, the group $\mathrm{Bir}^G(S)$ is generated by two or three Geiser involutions whose base points lie on the unique G-fixed line and by a subgroup of $\mathrm{Aut}(S)$ isomorphic to:

• (i) $S_3$ if S is of type V, VIII;

• (ii) if S is of type VI;

• (iii) if S is of type III, IV.

The group $\mathrm{Bir}^G(S)$ of the very general non-G-birationally superrigid minimal Del Pezzo G-surface of degree 3 with $G \simeq S_3$ is not finite.

For the proof, see Sect. 4.1.

Theorem 1.4

Let G be a cyclic group and S be a minimal Del Pezzo G-surface of degree 3. Then S is G-birationally superrigid if and only if G is of order 6 of type $A_5+A_1$. More precisely, if S is not G-birationally superrigid, then G is isomorphic to one of the following:

• (i) a cyclic group of order 3 of type $3A_2$. The group $\mathrm{Bir}^G(S)$ is (infinitely) generated by the Geiser involutions whose base points lie on the unique G-fixed nonsingular cubic curve and by a subgroup of $\mathrm{Aut}(S)$ isomorphic to , if S is the Fermat cubic surface, or by $\mathrm{Aut}(S)$ itself otherwise.

• (ii) a cyclic group of order 6 of type $E_6(a_2)$. The group $\mathrm{Bir}^G(S)$ is (infinitely) generated by three Geiser involutions, the Bertini involutions whose base points lie on a G-invariant nonsingular cubic curve C and by a subgroup of $\mathrm{Aut}(S)$ isomorphic to , if S is the Fermat cubic surface, or by $\mathrm{Aut}(S)$ itself otherwise.

• (iii) a cyclic group of order 9 of type $E_6(a_1)$. The group $\mathrm{Bir}^G(S)$ is finitely generated by three Geiser involutions whose base loci are coplanar and by a subgroup of $\mathrm{Aut}(S)$ isomorphic to the dihedral group $D_{18}$.

• (iv) a cyclic group of order 12 of type $E_6$. The group $\mathrm{Bir}^G(S)$ is finitely generated by G, by a Bertini involution and by a Geiser involution whose base loci are aligned.

For the proof, see Sect. 4.2.

Theorem 1.5

Let G be a non-cyclic group and S be a minimal Del Pezzo G-surface of degree 2. Then S is G-birationally superrigid.

For the proof, see Sect. 5.1.

Theorem 1.6

Let G be a cyclic group and S be a minimal Del Pezzo G-surface of degree 2. Then S is G-birationally superrigid if and only if G is one of the following:

• (i) a group of order 2 of type $A_1^7$;

• (ii) a group of order 6 of types $E_7(a_4), A_5 + A_1, D_6(a_2)+A_1$;

• (iii) a group of order 14 of type $E_7(a_1)$;

• (iv) a group of order 18 of type $E_7$.

Moreover, if S is not G-birationally superrigid, then G is isomorphic to one of the following:

• (v) a cyclic group of order 4 of type $2A_3+A_1$. The group $\mathrm{Bir}^G(S)$ is generated by infinitely many Bertini involutions whose base loci lie in the unique G-fixed nonsingular curve of genus one and by a subgroup of $\mathrm{Aut}(S)$ isomorphic to , if S is of type II, or by $\mathrm{Aut}(S)$ itself otherwise.

• (vi) a cyclic group of order 12 of type $E_7(a_2)$. The group $\mathrm{Bir}^G(S)$ is generated by two Bertini involutions and by a subgroup of $\mathrm{Aut}(S)$ isomorphic to .

For the proof, see Sect. 5.2.

Corollary 1.7

Let G be a cyclic group and S be a minimal Del Pezzo G-surface of degree smaller than 3. Then, S is G-birationally superrigid if and only if the group $\mathrm{Bir}^G(S)$ of G-birational automorphisms is finite.

Proof

It is an immediate corollary of Theorems 1.4 and 1.6. In particular, see Lemmas 4.9, 4.11 and 5.3. The authors are not aware of a proof that does not rely on the above classification.$\square$

In the paper we also provide explicit equations for the listed Del Pezzo surfaces S and the generators of the group $\mathrm{Bir}^G(S)$, unless it coincides with $\mathrm{Aut}^G(S)$. The types of the G-surfaces appearing in Theorems 1.3, 1.4 and 1.6 are described in full detail in Lemma 4.5, Propositions 4.7 and  5.2. For convenience, we summarise the contents of Theorems 1.3, 1.4 and 1.6 in Tables 1 and 2.

Table 1 Minimal Del Pezzo G-surfaces of degree 3 which are not G-birationally superrigid

Table 2 Minimal Del Pezzo G-surfaces of degree 2 which are not G-birationally superrigid

The structure of the paper is as follows: in Sect. 3 we rewrite in full detail the proof of the G-equivariant version of the above-mentioned Segre–Manin theorem, see Theorem 3.1. Note that the statement is essentially proved in [5, Corollary 7.11]. Building on this result, we classify the minimal Del Pezzo G-surfaces of degree 3 and 2 which are not G-birationally superrigid in Sects. 4 and 5 respectively.

2 Preliminaries

Let S be a nonsingular surface. A linear system on S is mobile if its fixed locus does not contain any divisorial component. The pair is the datum of a nonsingular surface S, a $\mathbb {Q}$-divisor D whose coefficients are at most 1 and a mobile linear system , or equivalently one of its general members. Let $\alpha :\widetilde{S} \rightarrow S$ be a birational morphism. For each prime divisor $E_i$ of $\widetilde{S}$ there exists a coefficient , called discrepancy, such that the following relation holds:

In particular, observe that the multiplicity of at a point $p \in S$ equals , where E is the exceptional divisor of the blow-up of S at p.

A pair is canonical if for any exceptional divisor E and for any $f:\widetilde{S} \rightarrow S$ birational morphism. A pair is called log Calabi–Yau if .

Let G be a finite group of automorphisms acting effectively on a surface S. In the introduction we have already recalled the definition of a G-rational map. This concept must not be confused with that of a G-equivariant map, i.e., a birational map which makes the following diagram commute:

for every $g \in G$.

The degreed of a Del Pezzo surface S is defined to be the self-intersection number of the canonical class $K_S$, in symbols $d{:=}K_S^2$. We briefly recall some properties of Del Pezzo surfaces of degree $\leqslant 3$, see for instance [6, Chapter III, Theorem 3.5].

• A Del Pezzo surface S of degree 1 is a nonsingular hypersurface of degree 6 in the weighted projective space $\mathbb {P}(1,1,2,3)$, embedded via the third pluricanonical linear system . Via the linear system , S can be realised as a double cover of the singular quadric $\mathbb {P}(1,1,2)$ branched along a nonsingular sextic curve. In particular, since the double cover is canonical, its deck transformation $\tau$ is a central element in the group of automorphisms $\mathrm{Aut}(S)$, see also [5, Section 6.7].

  

• A Del Pezzo surface S of degree 2 is a nonsingular hypersurface of degree 4 in the weighted projective space $\mathbb {P}(1,1,1,2)$, embedded via the second pluricanonical linear system . Via the canonical map, S can be realised as a double cover of $\mathbb {P}^2$ branched along a nonsingular quartic curve. In particular, since the double cover is canonical, its deck transformation $\tau$ is a central element in the group of automorphisms $\mathrm{Aut}(S)$, see also [5, Section 6.6].

  

• A Del Pezzo surface S of degree 3 is a nonsingular hypersurface of degree 3 in the projective space $\mathbb {P}^3$, embedded via the anticanonical linear system .

  

3 G-equivariant Segre–Manin theorem

In this section we present the proof, essentially due to Dolgachev and Iskoviskikh, of the following G-equivariant version of a classical arithmetic theorem by Segre [9] and Manin [8] (cf. also [2, Section 1.5]).

Theorem 3.1

(G-equivariant Segre–Manin theorem [5, Section 7.3]) Every minimal Del Pezzo G-surface S of degree $d \leqslant 3$ is G-birationally rigid.

The main ingredients of the proof are Noether–Fano inequalities, which in modern language recast the failure of birational superrigidity in terms of the existence of a non-canonical log Calabi–Yau pair.

Theorem 3.2

(Noether–Fano inequalities [3, Theorem 3.2.1 (ii), Theorem 3.2.6 (ii)]) Let G be a finite group, S and $S'$ be two minimal G-surfaces and $\varphi :S \dashrightarrow S'$ be a G-birational map. Suppose S is a minimal Del Pezzo surface and let be a G-invariant mobile linear system on S defined in the following way:

• if $S'$ is a Del Pezzo G-surface, then is the strict transform via $\varphi ^{-1}$ of the linear system |H|, where H is a very ample multiple of $-K_{S'}$;

• if is a G-conic bundle and H is a very ample G-invariant divisor of C, then is the strict transform via $\varphi ^{-1}$ of the linear system $|\psi ^*(H)|$.

Then, there exists a positive rational number $\lambda$ such that

and the following statements hold:

• (i) If $S'$ is a Del Pezzo surface and is canonical, then $\varphi$ is biregular.

• (ii) If $S'$ is a conic bundle, then is not canonical.

Proof of Theorem 3.1

Let $\varphi :S \dashrightarrow S'$ be a G-birational non-biregular map to a minimal G-surface $S'$. In order to prove that S is G-birationally rigid we need to exhibit a G-birational map $\sigma :S\dashrightarrow S$ such that is a G-biregular map.

Step 1 (non-canonical log Calabi–Yau pair). By Theorem 3.2, the existence of $\varphi$ is equivalent to the existence of a mobile G-invariant linear system on S such that

• (log Calabi–Yau) ;

• (not canonical singularities) the pair is not canonical.

Since $K_S$ generates $\mathrm{Pic}^G(S)$ in degree $\leqslant 3$, we can suppose $\lambda = \frac{1}{n}$ for some $n \in \mathbb {N}$.

Step 2 (orbit of length $\leqslant 3$). The proof of Lemma 3.4 implies that there exists a G-orbit O contained in the non-canonical locus of the log Calabi–Yau pair such that

Lemma 3.5 grants that the length of O is strictly less than the degree d of S.

Step 3 (Geiser and Bertini involution). By hypothesis, the degree of S is at most 3 and we are left with few possibilities:

Case 1. O consists of a single G-fixed point p and the degree of S is either 2 or 3. Let $\pi :\widetilde{S} \rightarrow S$ be the blow-up of S at p with exceptional divisor E. Then, the surface $\widetilde{S}$ is a Del Pezzo surface of degree 1 or 2 if S has degree 2 or 3 respectively (cf. Lemma 3.7), and it is endowed with a G-action via pullback of the G-action on S. These surfaces are endowed with a central G-invariant biregular involution $\tau$, which descends to a G-birational non-biregular involution $\sigma _1$ on S, named Bertini or Geiser involution respectively. The defined G-birational maps are collected in the following diagram:

Let a, b, c, d be integers such that $\tau ^*(H)\sim aH+bE$ and $\tau ^*(E)\sim cH+dE$, where is the pullback of the ample generator of $\mathrm{Pic}^G(S)$. Then, we obtain

Note in particular that $c>0$, because E is not $\tau$-invariant and so is not contracted by $\pi$: by the ampleness of $-K_S$, we obtain

Since $\tau$ preserves the canonical class , we obtain also that $a-c=1$, so that

Case 2. Oconsists of two points$p_1$and$p_2$and the degree ofSis 3. Analogously, the blow-up of S at $p_1$ and $p_2$ is a Del Pezzo surface of degree 1 endowed with a G-equivariant involution which descends to a non-biregular Bertini involution on S, denoted $\sigma _1$.

In all the cases, the Noether–Fano inequalities (cf. Lemma 3.4) force with $k_1 <n$.

Step 4 (inductive step). By Theorem 3.2, either is G-biregular or the pair is not canonical. In the latter case, we can repeat the above arguments and construct a sequence of Bertini or Geiser G-involutions $\sigma _1, \ldots , \sigma _s$ on S such that is non-biregular and again, by Theorem 3.2, the mobile pair , with $k_s < k_{s-1}$, is not canonical. However, if $s>n$, then the mobile linear system would not be $\mathbb {Q}$-linearly equivalent to an effective divisor, which is a contradiction. Hence, there exists an integer s such that $\varphi _s$ is G-biregular. We conclude that S is G-birationally rigid.$\square$

Corollary 3.3

Let S be a minimal Del Pezzo G-surface of degree 3 (resp. 2). Then, every G-birational map is a composition of a G-biregular map, Geiser and/or Bertini involutions (resp. a G-biregular map and Bertini involutions).

We now prove the lemmas used in the proof of Theorem 3.1.

Lemma 3.4

Let S be a G-surface and be a G-pair, i.e., is a G-invariant mobile linear system. If is not canonical, then there exists a G-orbit O in S such that

i.e., the multiplicity of each point of O on is greater than 1.

Proof

Let $\alpha :\widetilde{S} \rightarrow S$ be a G-equivariant log resolution of the pair . This means that $\alpha$ is a G-equivariant birational morphism such that the fixed locus of the pullback linear system has simple normal crossing. We prove the statement by induction on the number s of G-equivariant blow-ups through which $\alpha$ factors. If $\alpha$ is the blow-up of S at a single G-orbit O with exceptional divisor E, then

Since the pair is not canonical, by definition . Suppose now that , where $\alpha _i$ are a composition of iG-equivariant blow-ups:

$$\begin{aligned} \alpha :\widetilde{S} \xrightarrow {\,\alpha _{s-1}\,} S_1 \xrightarrow {\,\alpha _1\,}S. \end{aligned}$$

Let $O'$ be the centre of the blow-up $\alpha _1$ with exceptional divisor $E_1$. Then, either , or . In the latter case, since the pair is not canonical, a fortiori the pair is not canonical, but by induction hypothesis there exists $O_1 \subseteq S_1$ such that . This implies that for $O{:=}\alpha _1(O_1)$.$\square$

Lemma 3.5

Let S be a minimal Del Pezzo G-surface of degree d. If $\varphi :S \dashrightarrow S'$ is a non-biregular G-birational map, then the G-orbit O defined in Lemma 3.4 has length |O| strictly smaller than d.

Proof

Let be the linear system defined in Theorem 3.2. Consider $C_1$ and $C_2$ two general G-invariant $\mathbb {Q}$-divisors of . For any G-orbit O defined in Lemma 3.4, the following sequence of inequalities holds:

which implies $d > |O|$.$\square$

Remark 3.6

Lemma 3.5 implies immediately that any Del Pezzo G-surface of degree 1 is G-birationally superrigid, see also [5, Corollary 7.11].

Lemma 3.7

Let S be a minimal Del Pezzo G-surface of degree d and be a mobile linear system on S such that . Let be a G-equivariant blow-up of S at a G-orbit O defined in Lemma 3.4. Then, $S'$ is a Del Pezzo surface, i.e. $-K_{S'}$ is ample.

Proof

By the Nakai–Moishezon criterion for amplitude [7, Theorem 1.2.23], it is enough to check that

• $(-K_{S'}. C)>0$ for any curve $C \subset S'$;

• $K_{S'}^2>0$.

Note that

In particular, we obtain that for any curve $C \subset S$ different from E

since is an ample linear system and because of Lemma 3.4. If $C=E$, then

Finally, $K_{S'}^2=K^2_S- |O|>0$, by Lemma 3.5.$\square$

4 G-birational superrigidity of cubic surfaces

Let G be a finite group of automorphisms acting effectively on a minimal Del Pezzo surface of degree 3. It is well known that any Del Pezzo surface of degree 3 is a nonsingular cubic surface embedded in via the canonical embedding and every automorphism of S lifts to an automorphism of $\mathbb {P}^3$. The 4-dimensional vector space V is a G-representation, unique up to scaling by a character of G.

The content of this section is the proof of Theorem 1.4. Proposition 4.1 is one of the main ingredients of the proof.

Proposition 4.1

A minimal Del Pezzo G-surface S of degree 3 is not G-birationally superrigid if and only if it admits either G-equivariant Geiser or Bertini involutions. This is equivalent to the existence on S of a G-fixed point, not lying on a line, or a G-orbit of length 2, not lying on a line or a conic in S and such that no tangent space of one point contains the other.

Proof

This is a corollary of Theorem 3.1 and Corollary 3.3. The second statement follows from Lemma 4.2.$\square$

Lemma 4.2

Let S be a nonsingular cubic surface.

• (i) A point p in S is the base locus of a Geiser involution if and only if no line contained in S passes through p.

• (ii) The points $\{p_1, p_2\}$ in S are the base locus of a Bertini involution if and only if

  • (a) there is no line in S passing through $p_1$ or $p_2$;

  • (b) there is no conic contained in S passing through $p_1$ and $p_2$;

  • (c) $p_i$ is not contained in the tangent space of S at , $i \ne j$.

Proof

Let $f:\widetilde{S}\rightarrow S$ be the blow-up of S at p or at the pair $\{p_1, p_2\}$ respectively. By construction of Geiser and Bertini involution, we just need to check that $\widetilde{S}$ is a Del Pezzo surface. Recall that a Del Pezzo surface is the blow-up of $\mathbb {P}^2$ at most at eight points in general position, namely if

• no three of them lie on a line;

• no six of them lie on a conic;

• no eight of them lie on a nodal or cuspidal cubic with one of them at the singular point.

See for instance [1, Exercise V.21.(1)]. Let $g:S\rightarrow \mathbb {P}^2$ be a blow-up of $\mathbb {P}^2$ at six points $q_1, \ldots , q_6$ in general position. The point p in S is the base locus of a Geiser involution if and only if:

• p does not lie in the exceptional locus of g;

• the strict transform $\widetilde{l}$ of the line l passing through $q_i$ and does not contain p;

• the strict transform $\tilde{c}$ of a conic c passing through five of the points $q_i$ does not contain p.

Equivalently, we require that no $(-1)$-curve contains p. Indeed, the g-exceptional lines and the curves $\widetilde{l}$ and $\tilde{c}$ are all the 27 $(-1)$-curves in S.

In order to construct a Bertini involution, we need to check in addition that the strict transform $\tilde{s}$ of a singular cubic curve s containing all the points $q_i$ does not contain both $p_1$ and $p_2$. Suppose on the contrary that such a curve $\tilde{s}$ exists. We distinguish two cases: either $q_i$ is a singular point of s or one of the $p_i$, say $p_1$, is a singular point of $\tilde{s}$. In the former case, $\tilde{s}$ is a conic. Indeed, it is a nonsingular rational curve with

Vice versa, if the points $\{p_1,p_2\}$ lie on a nonsingular conic c in S, then

where $\tilde{c}$ is the strict transform of c via f, and $F_1$ and $F_2$ are the f-exceptional divisors. Thus, $\widetilde{S}$ is not a Del Pezzo surface. In the latter case, $\tilde{s}$ is an anticanonical divisor, hence a hyperplane section singular at $p_i$. In particular, the tangent plane at $p_1$ contains both the points $p_1$ and $p_2$.$\square$

In the following Lemma 4.3, we show that orbits of length 2 lie on invariant lines passing through a fixed point for the action of G on S.

Lemma 4.3

Let S be a minimal cubic G-surface admitting an orbit of length 2, then G fixes a point in S.

Proof

Denote by $q_1$ and $q_2$ the points in the orbit of length 2 and by $l_{q_1q_2}$ the line passing through those points in $\mathbb {P}^3$. Note that the line $l_{q_1q_2}$ is G-invariant and it is not contained in S. Differently, it could be contracted, violating the minimality of G.

Moreover, the line $l_{q_1q_2}$ intersects S with multiplicity 1 at $q_1$ and $q_2$. Otherwise, if the multiplicity at one of the two points is $\geqslant 2$, then so it is at the other point due to the group action. However, this is a contradiction, since $l_{q_1q_2}$ would intersect S with multiplicity at least 4, while S has degree 3. This implies that the invariant line $l_{q_1q_2}$ intersects S in a third point, thus fixed by the action of G.$\square$

Our strategy to show that a nonsingular cubic surface is G-birationally superrigid is the following:

• find G-fixed points and orbits of length 2 aligned with them, see Lemma 4.3;

• if the conditions of Lemma 4.2 do not hold for these G-orbits, then S is G-birationally superrigid.

In view of the latter, recall that a point of intersection of three lines on a cubic surface is called Eckardt point. It is just the case to mention that a point p is an Eckardt point if and only if the intersection of its tangent space to S and S itself is the union of three lines passing through p.

Remark 4.4

Notice that if $\{p_1, p_2 \}$ is a G-orbit then condition (c) in Lemma 4.2 always holds, since otherwise the line between $p_1$ and $p_2$ is bitangent to S.

4.1 G-birational superrigidity for non-cyclic groups

Suppose now that G is non-cyclic. Minimal non-cyclic finite groups acting effectively by automorphisms on cubic surfaces and fixing a point have been classified by Dolgachev and Duncan [4]. Any cubic surface endowed with an action of such a group is projectively equivalent to a surface $S_{ab}$ defined by

$$\begin{aligned} F_{ab} = t_0^3 + t_1^3 + t_2^3 + t_3^3 + t_0t_1(at_2 + bt_3), \end{aligned}$$

(1)

where a and b are parameters, and the fixed point is , see [4, Theorem 8.1]. In particular, G is a subgroup of the stabiliser of the point $p_0$. Since $F_{ab}$ specialises to the Fermat cubic equation $F_{00}$, G is a subgroup of the stabiliser of the point $p_0$ in $\mathrm{Aut}(S_{00})$, see the proof of [4, Theorem 8.1]. The automorphism group of the Fermat cubic surface is , where $S_4$ is the group of permutations of the variables and $3^3$ is the 3-torsion group of generated for instance by the following automorphisms:

where $\epsilon _3$ is a primitive third root of unity. The stabiliser of the point $p_0$ is , where $K_4$ is the non-normal Klein subgroup of $S_4$ generated by (12) and (34) and $3^2$ is generated by $\sigma$ and $\rho$.

In particular, the skew lines and are G-invariant, since they are invariant under the action of . The intersection $l_1\cap S_{ab}$ consists of three points $p_0$, and . In particular,

As the values of the parameters (a, b) vary, we have the following cases.

Type$a=b=0$. The surface $S_{00}$ is the Fermat cubic surface. The points $p_i$ are Eckardt points. No orbit can be the base locus of a Geiser or a Bertini involution. By Theorem 3.1, we conclude that $S_{00}$ is G-birationally superrigid.

Type$a^3=b^3\ne 0$. Up to a linear change of coordinates, we can suppose that $a=b\ne 0$. The group G is isomorphic to or $S_3$, where $S_3$ is generated by $\sigma \rho ^2$ and (12), and 2 is generated by (34), see [4, Theorem 8.1, Case 3.2.]. Hence, the only fixed point is the Eckardt point $p_0$ and the only invariant line through $p_0$ is $l_1$. Note that the surface $S_{ab}$ is of type VI in the sense of [5, Table 4] and the automorphism group of $\mathrm{Aut}(S_{ab})$ is isomorphic to . We consider the cases and $G \simeq S_3$ separately.

• . The conic passes through the length-two orbit $\{p_1, p_2\}$. By Lemma 4.2 and Theorem 3.1, we conclude that $S_{ab}$ is G-birationally superrigid.

• $G \simeq S_3$. The fixed points $p_1$ and $p_2$ are not Eckardt points. Therefore, $S_{ab}$ is not G-birationally superrigid and the group $\mathrm{Bir}^G(S_{ab})$ is generated by $\mathrm{Aut}(S_{ab})$ and the two Geiser involutions with base locus $p_1$ and $p_2$ respectively. The equations of these Geiser involutions and the infinitude of the group $\mathrm{Bir}^G(S_{ab})$ for the very general surface $S_{ab}$ are discussed in the following paragraphs.

Type$a^3 \ne b^3$. The group G is isomorphic to $S_3$, see [4, Theorem 8.1, Case 3.1]. The only fixed points are $p_0, p_1, p_2$. None of them is an Eckardt point and the only invariant line through $p_i$ is $l_1$. Therefore, $S_{ab}$ is not G-birationally superrigid and the group $\mathrm{Bir}^G(S_{ab})$ is generated by G-biregular automorphisms of $S_{ab}$ and three Geiser involutions with base loci contained in $l_1\cap S_{ab}$.

The Geiser involutions are given by the equations

We complete the list of generators, computing the normaliser $N_{\mathrm{Aut}(S_{ab})}(G)$ of G in $\mathrm{Aut}(S_{ab})$. We adopt the surface type convention of [5].

Lemma 4.5

The normaliser of G in $\mathrm{Aut}(S_{ab})$, denoted $N_{\mathrm{Aut}(S_{ab})}(G)$, is isomorphic to , if $S_{ab}$ is of type III or IV, or to $S_3$, if $S_{ab}$ is of type V or VIII.

Proof

Due to [5, Theorem 6.14], the group $\mathrm{Aut}(S_{ab})$ is one of the following.

• Type III. , where $H_3(3)$ is the Heisenberg group of unipotent -matrices over the finite field $\mathbb {F}_3$, see Sect. 4.2, Type $E_6$, for explicit generators. The generator of 4 conjugates the non-conjugate subgroups of type $S_3$ in , see [5, Theorem 6.14, Type III]. We conclude that $N_{H_3(3)\rtimes 4}(S_3)=N_{H_3(3)\rtimes 2}(S_3)$.

• Type IV. . It contains two non-conjugate subgroups isomorphic to $S_3$, normalized by the subgroups isomorphic to obtained from the previous ones by adding the central element, see [5, Theorem 6.14, Type III].

• Type V. $\mathrm{Aut}(S_{ab}) \simeq S_4$. Any subgroup isomorphic to $S_3$ is a non-normal maximal subgroup of $S_4$.

• Type VIII. $\mathrm{Aut}(S_{ab}) \simeq S_3$. $\square$

Let G be again the group of biregular automorphisms acting minimally on $S_{ab}$ with a fixed point $p_0$ and isomorphic to $S_3$. The following lemma establishes the infinitude of the group of G-birational automorphisms $\mathrm{Bir}^G(S_{ab})$ for the very general surface $S_{ab}$.

Let be the hypersurface given by the equation , see equation (1), and be the divisor in (equivalently ). Denote by the family of cubic surfaces $S_{ab}$ and by that of surfaces $S_{ab}$ with the property that $a=b$ (equivalently $a=\epsilon ^i_3 b$). The Geiser involutions $\varphi _{p_i}$ on $S_{ab}$ glue together to birational involutions of and respectively, as their equations are polynomial in (a, b).

Lemma 4.6

The group $\mathrm{Bir}^G(S_{ab})$ is not a finite group for the very general surface $S_{ab}$ in and in .

Proof

Let $\Delta$ be the diagonal in and be the graph of the composition in . There is an induced projection morphism

Define the (closed) algebraic subset

Note that the locus of surfaces $S_{ab}$ with infinite $\mathrm{Bir}^G(S_{ab})$ contains . Therefore, if there exists $(a_0, b_0)\in \mathbb {C}^2_{(a,b)}$ such that $\mathrm{Bir}^G(S_{a_0b_0})$ is not finite, then $C_n$ is a proper closed subset of $\mathbb {C}^2_{(a,b)}$ and the lemma holds.

We claim that $\mathrm{Bir}^G(S_{11})$ is not finite, i.e., we can choose $(a_0, b_0)$ equal to (1, 1). To this aim, recall the following facts:

• for any $p\in S_{ab}$ the point $\varphi _{p_i}(p)$ is aligned with $p_i$ and p;

• the involutions $\varphi _{p_1}$ and $\varphi _{p_2}$ fix the pencil of cubic curves

  

Fix such that $C_{(\lambda :\mu )}$ is nonsingular. Observe that the point $p_0$ is an inflection point of $C_{(\lambda :\mu )}$. Due to the previous facts, the following relations for the elliptic curve $(C_{(\lambda :\mu )},p_0)$ hold:

In particular,

One can check (use MAGMA) that for a suitable choice of (e.g.), the point $p_1$ is not a torsion point. This implies that has infinite order in $S_{11}$.

The same proof holds for since $S_{11} \subset \mathscr {S}'$.$\square$

Open Question

Is the group $\mathrm{Bir}^G(S_{ab})$ not finite for any $(a,b)\ne (0,0)$?

4.2 G-birational superrigidity for cyclic groups

In this section, we discuss the birational superrigidity of minimal cubic surfaces endowed with the action of a finite cyclic group G. Dolgachev and Iskovskikh classified these groups in [5]. For the convenience of the reader, we recall their result.

Here and in the following we denote by $\epsilon _n$ a primitive n-th root of unity.

Proposition 4.7

([5, Corollary 6.11]) Let $S=V(F)$ be a nonsingular cubic surface, endowed with a minimal action of a cyclic group G of automorphisms, generated by g. Then, one can choose coordinates in such a way that g and F are given in the following list:

• (i) $3A_2$, order 3, ,

  $$\begin{aligned} F=t^3_0+t^3_1+t^3_2+t^3_3+\alpha t_0 t_1 t_2; \end{aligned}$$

• (ii) $E_6(a_2)$, order 6, ,

  $$\begin{aligned} F=t^3_0+t^3_1+t^3_3+t_2^2(\alpha t_0+t_1); \end{aligned}$$

• (iii) $A_5 + A_1$, order 6, ,

  $$\begin{aligned} F=t^2_3t_1+t_0^3+t_1^3+t_2^3+\lambda t_0 t_1 t_2; \end{aligned}$$

• (iv) $E_6(a_1)$, order 9, ,

  $$\begin{aligned} F=t^2_3t_1+t^2_1t_2+t^2_2t_3+t^3_0; \end{aligned}$$

• (v) $E_6$, order 12, ,

  $$\begin{aligned} F=t^2_3t_1+t^2_2t_3+t^3_0+t^3_1. \end{aligned}$$

We proceed with an analysis case by case.

Type$3A_2$. G fixes the nonsingular cubic curve

S is not G-birationally superrigid and the group $\mathrm{Bir}^G(S)$ is generated by biregular G-automorphisms of S and infinitely many Geiser involutions whose base locus points lie on the nonsingular cubic curve given by $t_3=0$.

The normaliser $N_{\mathrm{Aut}(S)}(G)$ of G in $\mathrm{Aut}(S)$ is the group $\mathrm{Aut}^G(S)$ of biregular G-automorphisms. If C is equianharmonic, i.e., it has an automorphism of order 6, then S is the Fermat cubic surface and (cf. Sect. 4.1): the normaliser $N_{\mathrm{Aut}(S)}(G)$ is isomorphic to . Otherwise, g is a central element of $\mathrm{Aut}(S)$, which is isomorphic to or $H_3(3){\rtimes }2$, where $H_3(3)$ is the Heisenberg group of unipotent -matrices over the finite field $\mathbb {F}_3$ (cubic surfaces of type III or IV; see [5, Table 4]). Then, the group $\mathrm{Aut}^G(S)$ coincides with $\mathrm{Aut}(S)$.

Type$E_6(a_2)$. The line is fixed. The intersection

consists of three fixed points. The intersections of their tangent spaces with the cubic surface are respectively

which are three cuspidal cubic curves (we can suppose without loss of generality that , otherwise S would be singular). There is only one further isolated fixed point on S, namely , which is an Eckardt point and whose tangent space is given by the equation $\alpha t_0 + t_1=0$.

An invariant line, which is not , belongs either to the pencil of lines through intersecting the line $l_2$ or to the pencil of lines through intersecting the line $l_2$. These pencils span respectively the planes $t_2=0$ and $t_3=0$. Orbits of length 2 lie on invariant lines, neither on $l_1$ (since it is tangent to the Eckardt point , thus $l_1\cap S=\{p\}$), nor on a line through (since the group G modulo the stabiliser of the plane $t_2=0$ acts on it as a cyclic group of order 3). On the other hand, the nonsingular cubic curve

is covered by orbits of length 2, since the group G modulo the stabiliser of the plane $t_3=0$ acts on it as a cyclic group of order 2.

We conclude that S is not G-birationally superrigid and that the group $\mathrm{Bir}^G(S)$ is generated by G-biregular automorphisms of S, three Geiser involutions with base loci contained in $l_2\cap S$, and infinitely many Bertini involutions, whose base locus points lie on the nonsingular cubic curve given by $t_3=0$. We complete the list of generators, computing the normaliser $N_{\mathrm{Aut}(S)}(G)$ of G in $\mathrm{Aut}(S)$.

Lemma 4.8

Proof

Note that S is a cyclic cover of degree 3 of $\mathbb {P}^2$ branched along a nonsingular cubic curve C, and G is generated by $g_1g_2$, where $g_1$ is the deck transformation of the cover and $g_2$ is the lift of the involution on C.

If S is the Fermat cubic surface, then G is generated by the element in the notation of Sect. 4.1 (surface of type I with $K=G \cap 3^3$ of dimension 1 and type II $3A_2$; see [5, Section 6.5.]). Given , we observe that $\tau \in N_{S_4}((12)) \simeq K_4$. Denoting the conjugation of g via by $c_h(g)$, we write

Hence, $N_{\mathrm{Aut}(S)}(G)$ is generated by the permutation (12) and the subspace of $3^3_{(a_0,a_1,a_2)}$ satisfying the equation $a_0 \equiv a_1 \,(\mathrm{mod}\, 3)$. In particular, .

If S is not the Fermat cubic surface, then S is a surface of type III or IV [5, Table 4] and $\mathrm{Aut}(S)$ is a central extension of $\mathrm{Aut}(C)$ via $g_1$. Therefore, $N_{\mathrm{Aut}(S)}(G)$ is a central extension of $N_{\mathrm{Aut}(C)}(g_2)$ via $g_1$, but since $g_2$ is central in $\mathrm{Aut}(C)$, we conclude that $N_{\mathrm{Aut}(S)}(G)=\mathrm{Aut}(S)$, or equivalently that .$\square$

Types$A_5 + A_1$, $E_6(a_1)$and$E_6$. In the last few cases, i.e., $A_5 + A_1$, $E_6(a_1)$ and $E_6$, the group G acts on $\mathbb {P}^3$ by means of four distinct characters. In particular, the points and are the only fixed points in $\mathbb {P}^3$. The only invariant lines are those interpolating pairs of points , where $i \ne j$, shortly written . Note that eventual orbits of length 2 lie on .

Type$A_5 + A_1$. The only fixed point in S is the Eckardt point $p_3$. In the following table, we list all the invariant lines and the orbits that they cut on S.

Invariant lines		Orbits in
	$t_0^3+t_1^3=0$	orbit of length 3
	$t_0^3+t^3_2=0$	orbit of length 3
	$t^3_0=0$	fixed Eckardt point $p_3$
	$t^3_1+t_2^3=0$	orbit of length 3
	$t_3^2t_1+t^3_1=0$	fixed Eckardt point $p_3$ and orbit of length 2 given by:
	$t^3_2=0$	fixed Eckardt point $p_3$

Note that the conic

contains the only orbit of length 2 and the only fixed point in S is contained in a line. We conclude that S is G-birationally superrigid.

Type$E_6(a_1)$. All the fixed points in S are the points $p_1,p_2$ and $p_3$. They are not Eckardt points: by cyclic permutation of the variable it is enough to check that $T_{p_1}S\cap S$ is an irreducible cubic curve. Indeed,

The invariant lines $l_{p_1 p_2},l_{p_2 p_3}$ and $l_{p_1 p_3}$ intersect S in two fixed points, one of them necessarily with multiplicity 2. The invariant lines $l_{p_0 p_i}$, with $i=1,2,3$, are principal tangent lines at the singular point of the cuspidal cubic curves $T_{p_i}S\cap S$. We conclude that S is not G-birationally superrigid and the group $\mathrm{Bir}^G(S)$ is finitely generated by G-biregular automorphisms of S and three Geiser involutions with base loci $p_1,p_2$ and $p_3$ respectively. More explicitly, the Geiser involutions are given by

Although finitely generated, $\mathrm{Bir}^G(S)$ is not a finite group, as we show in the following lemma.

Lemma 4.9

The group $\mathrm{Bir}^G(S)$ is not a finite group.

Proof

It is enough to prove that the composition has infinite order. To this aim, recall the following facts:

• for any $p\in S$ the point $\varphi _{p_i}(p)$ is aligned with $p_i$ and p;

• the involutions $\varphi _{p_1}$ and $\varphi _{p_2}$ fix the pencil of cubic curves

  

Fix such that $C_{(\lambda :\mu )}$ is nonsingular and choose O an inflection point on $C_{(\lambda :\mu )}$. Due to the previous facts, the following relations for the elliptic curve $(C_{(\lambda :\mu )},O)$ hold:

In particular,

One can check (use MAGMA) that for a suitable choice of (e.g.), the point $p_2$ is not a torsion point. This implies that has infinite order.$\square$

We complete the list of generators of the group $\mathrm{Bir}^G(S)$, describing the group of G-biregular automorphisms of S. Note first that via the following change of coordinates

we can suppose that S is given by the equation

$$\begin{aligned} s_0^3+s_1^3+s_2^3+s_3^3=0 \end{aligned}$$

and a generator g of G acts via

Lemma 4.10

The normaliser of G in $\mathrm{Aut}(S)$, denoted $N_{\mathrm{Aut}(S)}(G)$, is isomorphic to the dihedral group $D_{18}$.

Proof

Recall that the automorphism group of a Fermat cubic is the group . Let $G'$ be the image of G in $S_4$, generated by the permutation (234), and $K{:=}G\cap 3^3$, generated by . The image of $N_{\mathrm{Aut}(S)}(G)$ is contained in $N_{S_4}((234))$, which is generated by (234) and (23) and isomorphic to $S_3$. Therefore, $N_{\mathrm{Aut}(S)}(G)$ is a subgroup of and admits a subgroup isomorphic to $S_3$.

The kernel of the projection $N_{\mathrm{Aut}(S)}(G) \rightarrow S_3$ is $3^3 \cap N_{\mathrm{Aut}(S)}(G) = K$. Indeed, the conjugation of g via an element is

i.e., . Since G is a subgroup of index 2 of , we conclude that .$\square$

Type$E_6$. In the following tables, we list fixed points and invariant lines and the orbits that they cut on S.

Fixed points	$T_{p_i}S$	$T_{p_i}S \cap S$	Eckardt point
$p_2$	$t_3=0$	$t^3_0+t^3_1=0$	yes
$p_3$	$t_1=0$	$t^2_2 t_3+t^3_0=0$	no

Invariant lines		orbits in
	$t_0^3+t_1^3=0$	orbit of length 3
	$t_0^3=0$	fixed Eckardt point $p_2$
	$t^3_0=0$	fixed point $p_3$
	$t^3_1=0$	fixed Eckardt point $p_2$
	$t_3^2t_1+t^3_1=0$	fixed point $p_3$ and orbit of length 2 given by:
	$t^2_2t_3=0$	fixed Eckardt point $p_2$ and fixed point $p_3$

Observe that the hypothesis of Lemma 4.2 (ii) holds for the orbit $\{q_1, q_2\}$. Indeed, the set $\{q_1, q_2\}$ is the only orbit of length 2 and $q_i$ are not Eckardt points, since

are cuspidal cubic curves. Moreover, the pencil of planes containing does not cut any conic on S and $q_i$ is not contained in the tangent space of , for $i \ne j$, by Remark 4.4. We conclude that S is not G-birationally superrigid and the group $\mathrm{Bir}^G(S)$ is generated by G-biregular automorphisms of S, a Bertini involution and a Geiser involution whose base loci are aligned: and $p_3$ respectively.

The Bertini involution with base points $q_1$ and $q_2$ is the deck transformation of the double cover

and it is given explicitly by

where

The Geiser involution with base point $p_3$ can be written as

Lemma 4.11

The group $\mathrm{Bir}^G(S)$ is not a finite group.

Proof

The proof is analogous to the one of Lemma 4.9. It is enough to prove that the composition has infinite order. Note that:

• for any $p\in S$ the point $\varphi _{p_3}(p)$ is aligned with $p_3$ and p;

• for any $p \ne p_3$, the points $\varphi _{q_1 q_2}(p)$ and p belong to a conic contained in the plane $\Pi _{q_1 q_2 p}$, spanned by $q_1,q_2$ and p, and tangent to $S \cap \Pi _{q_1 q_2 p}$ at $q_1$ and $q_2$;

• the involutions $\varphi _{p_3}$ and $\varphi _{q_1 q_2}$ fix the pencil of cubic curves

  

Fix such that $C_{(\lambda :\mu )}$ is nonsingular and choose O an inflection point on $C_{(\lambda :\mu )}$. Due to the previous facts, the following relations for the elliptic curve $(C_{(\lambda :\mu )},O)$ hold:

In particular,

One can check (use MAGMA) that for a suitable choice of (e.g.), the point $p_3$ is not a torsion point. This implies that has infinite order.$\square$

We complete the list of generators of the group $\mathrm{Bir}^G(S)$, observing that the only G-biregular automorphisms of S are the elements of G itself. Note that up to a change of coordinates [5, 6.5, Case 3, Type III], we can suppose that S is given by the equation

and a generator g of G acts via

The automorphism group of S is , where $H_3(3)$ is the Heisenberg group of unipotent -matrices over the finite field $\mathbb {F}_3$, generated by

and 4 is the cyclic group generated by

see [5, Theorem 6.14, Type III]. The group G is isomorphic to , where 3 is generated by , i.e., the centre of $H_3(3)$.

Lemma 4.12

The group G is self-normalising in $\mathrm{Aut}(S)$, i.e., the normaliser of G in $\mathrm{Aut}(S)$ is G itself.

Proof

If $G \subsetneq N_{\mathrm{Aut}(S)}(G)$, then $[H_3(3), H_3(3)] = G \cap H_3(3) \subsetneq N_{\mathrm{Aut}(S)}(G) \cap H_3(3)$ as $\langle \tilde{g}_4\rangle \subseteq G$. In particular, the image of $N_{\mathrm{Aut}(S)}(G)\cap H_3(3)$ via the quotient map $H_3(3) \rightarrow H_3(3)/[H_3(3), H_3(3)]\simeq 3^2$, generated by the image of $\tilde{g}_1$ and $\tilde{g}_2$, is non-trivial. Note that the element $\tilde{g}_4$ acts on $H_3(3)$ by conjugation via $(\tilde{g}_1, \tilde{g}_2)\rightarrow (\tilde{g}^2_2, \tilde{g}_1)$, see [5, Theorem 6.14, Type III]. As a result, we have

$$\begin{aligned} \tilde{g}_1^{-1}\tilde{g}_4\tilde{g}_1&=\tilde{g}_1^{-1}\tilde{g}^{-1}_2\tilde{g}_4\not \in G,\\ \tilde{g}_2^{-1}\tilde{g}_4\tilde{g}_2&=\tilde{g}_2^{-1}\tilde{g}_1\tilde{g}_4\not \in G,\\ (\tilde{g}_1\tilde{g}_2)^{-1} \tilde{g}_4(\tilde{g}_1\tilde{g}_2)&=\tilde{g}_2^{-1}\tilde{g}^{-1}_1\tilde{g}^{-1}_2\tilde{g}_1\tilde{g}_4\not \in G,\\ (\tilde{g}_1\tilde{g}^2_2)^{-1} \tilde{g}_4(\tilde{g}_1\tilde{g}^2_2)&=\tilde{g}_2\tilde{g}^{-1}_1\tilde{g}^{-1}_2\tilde{g}^{-1}_1\tilde{g}_4\not \in G. \end{aligned}$$

This implies that $N_{\mathrm{Aut}(S)}(G)\cap H_3(3)/[H_3(3),H_3(3)]=1$, which yields a contradiction. We conclude that G is self-normalising in $\mathrm{Aut}(S)$.$\square$

The results of this section are summarised in Theorem 1.4.

5 G-birational superrigidity of Del Pezzo surfaces of degree 2

In this section we prove Theorem 1.6 and we classify the Del Pezzo G-surfaces of degree 2 which are not G-birationally superrigid. Recall that a Del Pezzo surface S of degree 2 is a double cover of $\mathbb {P}^2$ branched over a nonsingular quartic curve. The surface S is a hypersurface of degree 4 in the weighted projective space $\mathbb {P}(1,1,1,2)$ given by the equation

where $F_4$ is a polynomial of degree 4. The covering map $\nu :S \rightarrow \mathbb {P}^2$ is then given by the projection on the first three coordinates and the ramification curve R is the intersection of S with .

As in the previous section, the proof of the Segre–Manin theorem (Theorem 3.1) implies that a minimal Del Pezzo G-surface of degree 2 is not G-birationally superrigid if and only if it admits a G-equivariant Bertini involution.

Lemma 5.1

Let S be a Del Pezzo surface of degree 2. Then, a point p is the base locus of a Bertini involution if and only if p lies neither on a $(-1)$-curve nor on the ramification locus of the double cover $\nu :S \rightarrow \mathbb {P}^2$.

Proof

The proof is analogous to that of Lemma 4.2. Recall that a Del Pezzo surface of degree 2 is a blow-up of $\mathbb {P}^2$ at points $q_1, \ldots , q_7$ in general position, see [1, Exercise IV.8.(10).(a)]. We need to check that the blow-up $\widetilde{S}$ of S at p is a Del Pezzo surface, or equivalently that the seven points $q_i$ and the image of p via the blow-down are in general position. We prove that if this is not the case, then p lies on a $(-1)$-curve or on the ramification locus. Indeed, note that the strict transform of a line passing through two of the points $q_i$ or that of a conic through five of them or that of a singular cubic curve through seven of them, with one of the $q_i$ at the singular point, is a $(-1)$-curve. Similarly, the strict transform of a singular cubic curve through all of the $q_i$, singular at p, is an anticanonical divisor, hence the pullback of a line via $\nu$. Since this curve is singular at p, then p lies on the ramification locus.

Conversely, if p lies on a $(-1)$-curve, the canonical class of the blow-up $S'$ of S at p has trivial intersection with the strict transform of the line, hence $-K_{S'}$ is not ample. On the other hand, if p lies on the ramification locus, then the preimage of the tangent line to the branch locus via $\nu$ is either an irreducible anticanonical divisor, singular only at p, i.e., the strict transform of a singular cubic passing through $q_i$, or the union of two $(-1)$-curves, if the line is bitangent to the branch locus.$\square$

Our strategy to identify birational superrigid G-surfaces will then consist in finding the fixed points of the given G-action and checking if these points lie on the ramification locus or on $(-1)$-curves. Recall that $(-1)$-curves on Del Pezzo surfaces of degree 2 are contained in the preimage of a bitangent line of the branched quartic in $\mathbb {P}^2$.

5.1 G-birational superrigidity for non-cyclic groups

The minimal non-cyclic groups G acting on S and fixing a point have been classified by Dolgachev and Duncan, the possible fixed points lie either on the ramification curve or they are the intersection of four $(-1)$-curves, see cases 2A and 2B of [4, Theorem 1.1]. Therefore, S is G-birationally superrigid by Theorem 3.1 and Lemma 5.1. This concludes the proof of Theorem 1.5. It remains to analyse cyclic groups.

5.2 G-birational superrigidity for cyclic groups

We describe the fixed locus of minimal cyclic groups G according to Dolgachev and Iskoviskikh classification. As before, we stick to their notation. Recall in particular that $\epsilon _n$ is a primitive n-th root of the unit and $F_i$ is a polynomial of degree i.

Proposition 5.2

([5, Section 6.6]) Let $S = V(F)$ be a Del Pezzo surface of degree 2, endowed with a minimal action of a cyclic group G of automorphisms, generated by g. Then, one can choose coordinates in such a way that g and F are given in the following list:

• (i) $A^7_1$, order 2, ,

  

• (ii) $2A_3+A_1$, order 4, ,

  

• (iii) $E_7(a_4)$, order 6, ,

  

• (iv) $A_5+A_1$, order 6, ,

  $$\begin{aligned} F = t_3^2 +t_2^3 t_0 + t_0^4 +t_1^4 + at_0^2 t_1^2; \end{aligned}$$

• (v) $D_6(a_2)+A_1$, order 6, ,

  

• (vi) $E_7(a_2)$, order 12, ,

  $$\begin{aligned} F = t_3^2 + t_0^4 + t_1^4 + t_0t_2^3; \end{aligned}$$

• (vii) $E_7(a_1)$, order 14, ,

  $$\begin{aligned} F = t_3^2 + t_0^3t_1 + t_1^3 t_2 + t_2^3t_0 ; \end{aligned}$$

• (viii) $E_7$, order 18, ,

  $$\begin{aligned} F = t_3^2 + t_0^4 + t_0t_1^3 + t_2^3t_1. \end{aligned}$$

We proceed with an analysis case by case.

Type$A^7_1$. The generator g is the standard Geiser involution of the surface S leaving the ramification curve fixed. Hence, the surface is G-birationally superrigid.

Type$2A_3+A_1$. The curve is fixed by the action of G. It is the preimage of the line under the double cover $\nu$. The intersection of l with the branched quartic

is simply given by . Notice that the polynomial $F_4$ has four distinct roots as C is nonsingular, hence there are four distinct intersection points and l is not a bitangent line of C. This implies that every point in the preimage of l is the base locus of a Bertini involution with the exception of the preimages of the four points of intersection with C and of the points of intersection with the bitangent lines of C. In other words, $\mathrm{Bir}^G(S)$ is generated by G-automorphisms and infinitely many Bertini involutions, in particular S is not G-birationally superrigid.

To complete the list of generators of $\mathrm{Bir}^G(S)$ it suffices to compute the normaliser $N_{\mathrm{Aut}(S)}(G)$. Notice that up to a linear change of coordinates in the variables $t_0, t_1$, the equation F can be written as

$$\begin{aligned} F = t_3^2 + t_2^4 + t_0^4 + at_0^2t_1^2 + t_1^4. \end{aligned}$$

The automorphism group $\mathrm{Aut}(S)$ depends on the parameter a and in each case we compute the normaliser $N_{\mathrm{Aut}(S)}(G)$ of G in $\mathrm{Aut}(S)$:

• if $a = 0$, then (cf. [5, Theorem 6.17, Type II]), where 2 is generated by , the symmetric group $S_3$ is generated by the transpositions

  

  and $4^2$ is generated by

  

  subject to the following relations:

  $$\begin{aligned} \tau g_2 \tau = g_2, \quad \tau g_1 \tau = g_1^{-1}g_2^{-1} = g_1^3g_2^3. \end{aligned}$$

  In particular, the group G is generated by $g=\gamma g_2$. Notice that $\langle g_2 \rangle$ is central in and therefore it is central in . Since

  

  we conclude that .

• if $a = \pm 2\sqrt{3}\,i$, then (cf. [5, Theorem 6.17, Type III]), where 2 is generated by and $4A_4$ is a central extension of the alternating group $A_4$ generated by

  

  Since c is central in $\mathrm{Aut}(S)$ and $g = \gamma c$, we conclude that $N_{\mathrm{Aut}(S)}(G) = \mathrm{Aut}(S)$.

• if $a \ne 0, \pm 2\sqrt{3}\,i$, then , where $AS_{16}$ is a non-abelian group of order 16 isomorphic to (cf. [5, Tables 1 & 6]). The generators of $\mathrm{Aut}(S)$ coincide with that of the previous case with the exception of the generator $g_3$. Hence, as in the previous case, g is a central element and $N_{\mathrm{Aut}(S)}(G) = \mathrm{Aut}(S)$.

Type$E_7(a_4)$. The fixed locus is given by and . In particular all fixed points lie on the ramification curve and therefore they do not give rise to Bertini involutions, thus S is G-birationally superrigid.

Types$A_5+A_1$, $D_6(a_2)+A_1$, $E_7$and$E_7(a_1)$. The fixed locus of each of these groups is contained in the set

of points on the ramification curve, hence S does not admit any Bertini involution and it is G-birationally superrigid.

Type$E_7(a_2)$. The fixed locus consists of the point lying on the ramification curve and two points

These points are mapped of the point via of the covering map $\nu$. The branch locus is given by

Suppose is a point in C whose tangent line

passes through p, then . This intersection consists of 12 distinct points

In other words, the lines tangent to C and passing through the possible q are given by

which are pairwise distinct and intersect C in three distinct points each, and hence, are not bitangent lines. Therefore $p_1$ and $p_2$ are not in any $(-1)$-curve and it follows that S is not G-birationally superrigid.

The Bertini involution with base point $p_1$ is the deck transformation of the map

and it is given explicitly by

where

Similarly, the involution with base point $p_2$ is the deck transformation of the map

therefore

where

Lemma 5.3

The group $\mathrm{Bir}^G(S)$ is not a finite group.

Proof

The proof is analogous to the one of Lemmas 4.9 and  4.11. It is enough to prove that the composition has infinite order. To this aim, note that the involutions $\varphi _{p_1}$ and $\varphi _{p_2}$ fix the pencil of curves of genus one

In particular, for a general choice of , we have

In the chart , where $r_0$ is a root of the polynomial , the affine curve is the zero locus of a cubic equation in $\mathbb {C}^2$, and $C_{(\lambda :\mu )}$ is birational (thus isomorphic) to the (nonsingular) projective closure of in $\mathbb {P}^2$ with coordinates . Hence, we can identify the two curves. Let . By restricting the linear system defining the double cover $\psi _i$ to , one can check that the points $p_i$ and $\varphi _{p_i}(p)$ are contained in a conic, tangent to $C_{(\lambda :\mu )}$ at $p_i$ and . As in Lemmas 4.9 and  4.11, we deduce the following relations for the elliptic curve $(C_{(\lambda :\mu )}, O) \subseteq \mathbb {P}^2$:

In particular,

One can check (use MAGMA) that for a suitable choice of (e.g.$2\lambda ^3+17\mu ^3=0$ and $r_0=1/2$), the point $p_2$ is not a torsion point. This implies that has infinite order.$\square$

The automorphism group of S is , see [5, Table 6, Theorem 6.17, Type III]. Here $4A_4$ is a non-split central extension of $A_4$ by a cyclic group of order 4, more explicitly there exists an exact sequence

$$\begin{aligned} 0 \rightarrow 4 \rightarrow 4A_4 \rightarrow A_4 \rightarrow 0. \end{aligned}$$

Let $G'$ be the image of G in $A_4$ under the composition of quotient homomorphisms . Notice , since $G'$ is necessarily a cyclic group of $A_4$ whose order is a multiple of 3. It follows the image of $N_{2 \times 4A_4}(G)$ is contained in $N_{A_4}(3)$. Moreover, notice that $N_{A_4}(3)= 3$, as there are no proper normal subgroups in $A_4$ containing 3 and 3 is not normal in $A_4$. Finally, since is a central extension of a central extension of $A_4$, one obtains . The group $\mathrm{Bir}^G(S)$ is generated by G, the standard Geiser involution $\gamma$ and two Bertini involutions with base locus $p_1$ and $p_2$ respectively.

The cases above yield the proof of Theorem 1.6.