Abstract
The aim of this study was to develop a semi automatic image processing algorithm (AIPA) based on the simultaneous information provided by X-ray and radioisotopic images to determine the biokinetic models of Tc-99m radiopharmaceuticals from quantification of image radiation activity in murine models. These radioisotopic images were obtained by a CCD (charge couple device) camera coupled to an ultrathin phosphorous screen in a preclinical multimodal imaging system (Xtreme, Bruker). The AIPA consisted of different image processing methods for background, scattering and attenuation correction on the activity quantification. A set of parametric identification algorithms was used to obtain the biokinetic models that characterize the interaction between different tissues and the radiopharmaceuticals considered in the study. The set of biokinetic models corresponded to the Tc-99m biodistribution observed in different ex vivo studies. This fact confirmed the contribution of the semi-automatic image processing technique developed in this study.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Small-animal imaging (SAI) systems provide non-invasive methods of assaying biological structure and function in vivo, in order to characterize (spatially and temporally) ordinary or abnormal tissues (such as tumors). Taking into account their non-invasive nature, imaging systems permit serial assays through rodent models of human cancer, cardiovascular abnormalities, neurological disorders and other diseases [1].
A large number of in vivo SAI systems has become available over the last decade, including optical bioluminescence/fluorescence, single photon emission computed tomography (SPECT), positron emission tomography (PET), computed tomography (CT), ultrasound (US), magnetic resonance imaging (MRI) in its different variants, such as magnetic resonance spectroscopy (MRS), diffusion tensor imaging (DTI), functional MRI (fMRI), and others. These diverse approaches differ from each other either in characteristics of the imaging probes or detection techniques. An imaging probe can be considered as a biologically relevant signal suitable for detection by a specific imaging technique [2, 3].
A combined modality oriented to simultaneously provide structural information (MRI, CT, US) and functional information (for example, PET, SPECT, fMRI, and MRS), has been considered as the most desirable imaging analysis strategy [4,5,6].
Currently, there is a multimodal preclinical in vivo imaging system (Xtreme, Bruker) based on optical technology for imaging of radiopharmaceuticals, which unlike conventional nuclear imaging systems (SPECT), has an ultra-thin phosphor screen that functions as a scintillator, a CCD detector, and lacks of pulse height analyzer for discriminating the energies emitted by the radionuclide. Mainly, this device is utilized to analyze the presence of biomarkers that are usually applied as biosensors in different malignancies [7].
Several contrast agents (used as biomarker) have been developed over the last few years, with a major focus on molecular specificity to enable labeling of particular cells types associated to different disease processes. Recently, the complexes 99mTc-ethylenediamine-N,N´-diacetic acid/hydrazinonicotinamyl-Lys3-Bombesin (99mTc-BN) and 99mTc-ethylenediamine-N,N´-diacetic acid/hydrazinonicotinamyl-Glu[cyclo(Arg-Gly-Asp-d-Phe-Lys)]2 (99mTc-RGD2) have been reported as radiopharmaceuticals with major stability in human serum, with specific recognition to gastring releasing peptide receptor (GRPr) and integrins α(v)β(3) and α(v)β(5), respectively, which are very active in cancer cells. Integrins formed a large family of heterodimeric glycoprotein receptors. Each integrin heterodimer consists of an alpha (α) and a beta (β) subunit. The integrins α(v)β(3) and α(v)β(5) as well as the GRPr are over expressed in membrane cancer cells.
The aforementioned process can be characterized by means of a biokinetic mathematical model, obtained by SPECT image quantification [8,9,10].
A mathematical description of the time-dependent tissue uptake and tissue clearance after injection of contrast agents or radioactively-labeled tracers with suitable models (kinetic modeling), allows a detailed analysis of in vivo imaging corresponding to transporting and metabolism processes [11]. This analysis can provide quantitative information for several relevant parameters such as local blood volume, blood flow, distribution volumes, metabolic rates, binding potentials and so forth, simultaneously [12], [13]. Despite the remarkable imaging results offered by the Xtreme device, there is a lack of automatic system to obtain the regions of interest and their activity quantification needed to develop the mathematical models [14]. This condition may reduce the model accurateness and its reproducibility.
In this study, homogeneous regions of radiopharmaceuticals activity were determined to obtain the aforementioned models in an automatic manner. Today, this task is performed by using the free-hand tool for regions of interest selected by the user. Therefore, an automatic method could greatly enhance the accuracy of the modeling task. Biomedical image processing is the method proposed in this study for radiation activity quantification with scattering, background and attenuation corrections from the Xtreme images. [15].
The aim of this research was to develop an automatic image processing system to quantify the 99mTc-BN and 99mTc-RGD2 radiation activity from images acquired in a murine model using the multimodal preclinical in vivo imaging system Xtreme. The regions of interest were semi-automatically selected and the effect of scattering was removed by the method proposed in this study. Background as well as attenuation were also corrected. This image processing system was implemented in Matlab®, since its Image Processing Toolbox provides a wide range of advanced image-processing functions and interactive tools for enhancing and analyzing digital images [16]. The information generated by the automatic image-processing method was used to develop the biokinetic model of 99mTc-BN and 99mTc-RGD2 in the different anatomically-oriented regions of interest depending on the radiation activity accumulation.
2 Methods
2.1 Image Acquisition System
All the optical images were acquired with the preclinical multimodal in vivo imaging system Xtreme (Bruker) for small species, with two modes of acquisition: Radionuclide and X-Ray. Acquisition parameters of binning were 1 × 1 and field of view was 12.5 cm. For the radioisotopic images, a phosphor screen at exposure time of 5 min was used. X-ray images were acquired with a radiographic screen and an exposure time of 5.0 s. Parallel-hole collimator was used to reduce the effect of scattered radiation in either the analysis of attenuation-dispersion correction factors or to acquire radioistopic images of the mice. The X-ray parameters were: energy of 45 kVp, current of 497 µA and an aluminum filter of 0.8 mm.
All experiments including the tumor induction and the injection of 99mTc-BN and 99mTc-RGD2 followed the rules stated in the official norm NOM-062-ZOO-1999. Also, the protocol proposed to execute the animal experiments were evaluated and approved by an ethical committee.
2.2 Anisotropy Study
At the moment, there is no a formal anisotropy study for the Xtreme equipment. Even when CCD sensor array and parallel beam collimator are highly isotropic structures, there is the necessity of estimate the possible variation of radiation detector with respect to the incidence angle.
An anisotropy study based on an automatic image processing algorithm without the parallel-hole collimator was made by duplicate, using the images acquired by the Xtreme equipment of six 99mTc samples (n = 3). Samples of radionuclides with previously known activities were placed in equally-dimensioned wells (Depth: 10.67 mm, diameter: 6.35 mm). Subfigures named A1, B2, C3, D4, E5 and F6 in Fig. 1 correspond to six samples with known radiation activities served to construct the anisotropy study. These activities were 1.73, 3.47, 6.92, 13.87, 22.75 and 55 MBq/50 µL (n = 3).
The gray-scale intensity per pixel in eight sections of the scattering halo was quantified by an automatic image processing method (Fig. 1). These sections were determined by an algorithm that automatically calculated the counts per pixel by the sequential application of morphological image processing operations over the image. External and internal activity regions were determined based on the application of the following treatment sequence: histogram equalization, morphological opening and image binarization with two different thresholds (0.7 and 0.9) [16].
These treatments used two masks: one representing the actual activity in the well, and the second included the radiation scattering. Subtracting these two masks produced a halo that can be spliced in 8 equally-distributed sectors. Pixel intensity (measured by the gray-scale color representation) was added and correlated with the previously known radiation activity. Therefore, the radiation activity of eight sections was calculated. The intensity average and standard deviation of eight sections from each image were calculated by adding all the intensities within each region. Standard deviations lower than 5% in all regions (corresponding to statistical significance p < 0.05), indicated that Xtreme acquisition is isotropic.
2.3 Attenuation Factor Calculation
To calculate the Xtreme attenuation factor (AF) by the mouse thickness, a set of eight known 99mTc radiation activity (0.2 to 17.0 MBq/100 µl) samples (n = 3) were placed in wells in two different geometry groups.
The first experiment positioned a mouse between the plate and the imaging system sensor. The second one used the same known samples but for this particular case, no mouse was placed over the plate (Fig. 2). The radiation source was aligned in both experiments by using X-ray images. The sample was elevated to same position considered when the mouse was in the experiment. This condition was proposed to avoid blurring and crosstalk within the collimator. It should be considered that mice used in these experiments are between 1.0 and 2.0 cm width. Then no correction by organ deep was considered.
The radiation activity of each sample (with and without mouse) was quantified by a similar code to the one developed for determining the isotropy. The AF was calculated as the quotient of the total intensity including the mouse (IWM), divided by the total intensity without the mouse (IWOM). A linear function was used to correlate the AF with the radiation activity [15].
The percentage of radiation attenuation due to the mouse body was 64 ± 2% calculated from all the images acquired according to the methodology reported. This percentage was used as the attenuation correction factor (AF). The AF was used to correct the intensity of activity quantification in mice images according to the following expression:
The averaged attenuation value was 0.64 (±0.05). Then, a linear relationship between attenuated activity I A and the measured one I N . The calibration technique used to adjust the attenuation factor included the rat tissue.
2.4 Evaluation of Scattering and Calibration Factor
This study considered that radiation interacts with some organs and structures different to target organs. We assumed that these structures are dense enough to produce secondary radiation that scatters from the main zone where radiation is detected.
Even when only images obtained from Xtreme can be used to elucidate if radiations scatter or blurring is a consequence of detector, we have observed different radiation patterns on experiments. Therefore, we assumed that these variations are produced by scattered radiation instead of a detector characteristic (which should remain constant).
To calculate scattering and calibration factor, six different known 99mTc radiation activities (n = 3) were placed in wells of equal dimensions (depth: 10.67 mm, diameter: 6.35 mm). Six samples with known radiation activities served to construct the attenuation study. These activities were 16.43, 6.88, 3.42, 1.74, 0.95, 0.54 and 0.37 and 0.21 MBq/100 µL. For the case of the scattering and calibration factor, we used 3.09, 2.52, 1.62, 0.83, 0.34, 0.17 MBq/50 µL.
Using the Xtreme SAI, a set of images was acquired from each well.
A new automatic image processing algorithm was developed in Matlab to place a filled white circle with diameter (in pixels) equal to the diameter of the well in the gray-scale image (Ig). The diameter of the well in pixels was calculated using the information from an X-ray image. This image was represented as mask 1 (M1). The circle represents the region where the main radiation activity was emitted.
A second concentric (to the one placed in mask M1), exterior circle was developed to cover every pixel where radiation still appears, surrounding the original circle calculated by the masking based on M1. These pixels represent the scattered radiation around each well. This second filled circle produced the second binary mask (M2).
A third binary mask (M3), was obtained by subtracting M1 from M2. The set of these three masks M1, M2 and M3, as well as an example showing how they were applied on unprocessed image Ig are shown in Fig. 3. Image Itot represents the application of the mask M1 over Ig, obtained by the direct multiplication (pixel by pixel) between these two images. A similar procedure was followed to obtain the image Iact, that corresponds to the application of M2 over Ig. Finally, Idis represents the image where the scattered information can be quantified using the pixels represented in the gray-scale [16].
Normalized intensity (intensity/pixel) in each image was calculated. Total intensity per pixels of the total image (Int), the normalized intensity due to the activity in the well (INa) and the normalized intensity due to the scattering (INd), were also determined. From the collected information, two different relationships were analyzed: [I nt vs (I nt −I Nd )] and [(I Na −I Nd ) vs Activity]. For each relation, two different functions were fitted to obtain the scattering factor and the calibration factor, respectively.
A flow chart describing the sequence of steps needed to complete the image processing steps as well as the modeling method appears in Fig. 4.
2.5 Biokinetic Model Synthesis
Five athymic nude mice bearing the T47D tumor (breast cancer cells, average tumor area: 0.5 cm2), were injected with 99mTc-BN or 99mTc-RGD2 in the tail vein. Mice under 2% isoflurane anesthesia were placed in the supine position. Whole body radioisotopic and X-ray images were acquired at the same mice position with the Xtreme equipment. The image acquisition strategy obeyed the following sampling times: 0.0, 5.0, 10.0, 15.0, 20.0, 120.0 min and 24 h.
A different automatic image processing algorithm was developed in Matlab® to process both the radioisotopic and X-ray images. This new algorithm was proposed to quantify the radiation activity from heart, kidney 1, kidney 2, bladder and tumor. Radiation activity obtained from these images was compensated in background, attenuation and scattered radiation using the correction factors developed in previous experimental stages. The algorithm satisfied the next logical sequence:
-
(a)
Central coordinates of organs and tumor introduction: Central coordinates of image regions corresponding to areas of heart, kidneys, bladder and tumor were obtained from the radioisotopic image. A similar analysis to the one used to obtain M1 was used in this step. The corresponding coordinates were labeled (Xhe, Yhe), (Xk1, Yk1), (Xk2, Yk2), (Xbl, Ybl) and (Xtu, Ytu), respectively.
-
(b)
Organs selection and organ mask creation: After coordinate definition, the algorithm automatically fragmented the optic image into five independent images associated to each organ of interest (heart, kidney 1, kidney 2, bladder and tumor). These masks were obtained by the sequential application of morphological labeling and binarization operations. Five different binary mask images were created corresponding to each organ.
-
(c)
Tumor area and mask creations: Due to the variability of tumor morphology, its corresponding binary mask cannot be calculated automatically if it is not placed over the region where any of organs selected in the previous stage appeared. The tumor location was fixed to posterior legs. Therefore, no interference was observed in the acquired images. A similar sequence of binarization and labeling algorithms was used to determine the binary mask associated to the tumor. This part of the algorithm used the X-ray image. The region that characterizes the tumor position was obtained by using the anatomic references observed in X-ray image. However, the algorithm was prepared with the option of mask-correction by gathering the data obtained from the X-Ray and radioisotopic images.
-
(d)
Images multiplication (overlapping): After the determination of organ and tumor regions, their respective binary masks were overlapped to the radioisotopic image to characterize the particular radiation activity for each organ and the tumor. This step was executed by the application of a labeling procedure over each region determined in this step.
-
(e)
Intensity computing: Based on the separated images created in the last step, the algorithm computed the radiation intensity in counts per pixel of each organ and the tumor. These counts were named INhe, INk1, INk2, INbl and Intu, corresponding to heart, kidney 1, kidney 2, bladder and tumor.
-
(f)
Intensity correction by attenuation interference: A correction factor was applied to the intensities determined in the previous step. This factor was obtained from the AF analysis. A direct subtraction of the AF from counts INhe, INk1, INk2, INbl and INtu by IAhe, IAk1, IAk2, IAbl and IAtu, respectively, that corresponds to the attenuation of radiation intensity for heart, kidney 1, kidney 2, bladder and tumor.
-
(g)
Intensity correction by scattering interference: A second correction factor was applied to the intensities determined in the previous step using the information obtained in the scattering interference analysis. The direct subtraction of the factors IAhe, IAk1, IAk2, IAbl and IAtu from the true radiation activity associated to the biomarker proposed in this study. The intensity results were denominated: IDhe, IDk1, IDk2, IDbl, and IDtu, respectively.
-
(h)
Intensity to activity conversion: Finally, the application of calibration factor on IDhe, IDk1, IDk2, IDbl, and IDtu produced the real radiation activity results named Ahe, Ak1, Ak2, Abl, and Atu. This factor was used to convert the pixel intensity into radiation activity.
Once the radiation activity of 99mTc over time for each organ was obtained, a nonlinear Hammerstein-Wienner algorithm was used to develop the biokinetic model.
A bi-exponential function for each curve was fitted using the well-known theory of interaction between radiation and organic tissue. Activity (number of disintegrations per unit time), integrated over time, gives the total number of disintegrations (N), expressed per unit of initial activity in the studied source region (MBq h/MBq).
2.6 Statistical Analysis
Validation of the model obtained in this study used the kidneys’ activity quantification reported in previous articles [8, 9]. In those studies, similar quantification data were obtained from mice organs after complete dissection using the same radiopharmaceuticals. Student t test (p > 0.05) of two set of experiments with different standard deviation was considered to calculate the significance of similarity degree between experimental data.
2.7 Animal Care
All applicable international, national, and/or institutional guidelines for the care and use of animals were followed. Besides all procedures performed in studies involving animals were in accordance with the ethical standards of the institution (ININ) or practice at which the studies were conducted.
3 Results
3.1 Anisotropy Study
The intensity quantification results obtained from the anisotropy study are shown in Table 1. Six different images (with different initial radiation activity) were obtained from this study (Fig. 5). Each image was divided in 8 regions as explained in the methodology.
The average intensities quantified in all the 8 sections of a known-activity image is reported in Table 1, as well as the corresponding standard deviation. In all cases, this statistic parameter was less than 5% with respect to the average value of each image. This means that the 99mTc radioisotopic image acquired with the Xtreme has no anisotropy interference; therefore, no correction factor should be determined and applied to adjust the actual radiation activity.
In literature, anisotropy studies by image processing have been developed for many years. Several formal methods based on image filtering and deblurring have offered a formal method to correct the anisotropy effect [17, 18]. However, the automatic image processing method described in this study was an alternative to characterize the possible anisotropy effect.
Despite that, all results obtained in this study showed low standard deviation (<5.0%), there is still the option to apply the image tensor information to design anisotropic diffusion scale/spaces in order to reduce the effect of anisotropy.
3.2 Attenuation Factor Calculation
The attenuation correction method presented in this study uses a simple manner to take into consideration the presence of mice. In this case, the so-called linear attenuation coefficient was the selected form to model the attenuation effect.
The presence of collimator supports the selection of the linear attenuation coefficient model. However, this study did not consider the determination of attenuation map because the size of mice. However, the application of image processing methods may be simultaneously used to characterize this spatial distribution [15].
Results without attenuation and scatter corrections are not presented. The reported methods of radioactivity quantification from images always recommend the use of these corrections because the information collected by radioisotopic imaging systems does not meet the definition of a projection.
The gamma ray emissions collected by the systems are not linearly related to the sums of activity in the sample because of tissue attenuation. As a consequence, these attenuated projections results with artifacts and will not accurately reflect the true internal distribution.
Factors different from attenuation limit the quality of the images. These include spatial resolution, scattered radiation, and statistical fluctuations (image noise). The advances in nuclear imaging are directly tied to improving the quality and accuracy of the acquired projections either through better instrumentation or better correction algorithms.
The variation of mice depth is not so relevant. In average, the selected mice have similar dimensions with a standard deviation of 0.19 cm. This is less than 5% of 1.18 cm averaged depth. Even when a detailed study on the effect of mice depth can be interesting, the attenuation correction by the method used in this study is very recommended when activity determination from images is done, because gamma photons in optical imaging are subject to attenuation as they travel through the imaged object. This effect reduces the number of photons detected in each line of response. If the material properties of the object are known, the measurement along each line of response can be corrected for this attenuation effect. Although the magnitude of this correction for small animal subjects is much smaller than for humans (45 for a 40 cm diameter human), it is important to correct the data for quantitative analysis of the tracer distribution. The main advantage of using a global scale factor for attenuation correction is convenience. No transmission scans are needed and attenuation is assumed to be uniform for small animals such as mice. Moreover, soft tissue attenuation coefficients have a larger impact on Tc-99m studies because of its lower energy gamma rays [19].
3.3 Scattering Correction Factor
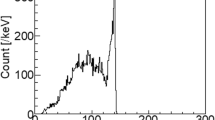
Figure 6 depicts the results obtained when the relation [I nt vs (I Na −I Nd )] was analyzed as well as its linear function regression. This parametric identification analysis yields to the following equation:
where a = 180.74892 counts/pixel, b = 0.06011 (counts/pixel)/(counts/pixel). The linear regression analysis produced a correlation coefficient of R2 = 0.98. Equation 2 was used in the activity quantification algorithm to eliminate the counts in the region of interest due to dispersion effect.
3.4 Calibration Factor
Figure 7 represents the results obtained for the relationship [(I Na −I Nd ) vs Activity] as well as its exponential function regression. This linear parametric identification analysis yields a correlation factor of 0.99. The equation that relates the activity to I Na −I Nd is:
where A = 3.75543e −24 MBq, C = 3.8187 counts/pixel, z = 0.08289 MBq.
The calibration factor described in Eq. 3 was used to convert the intensity corrected by radiation attenuation and dispersion to activity in MBq in the activity quantification algorithm. Notice that this calibration curve already considered the effect of 99mTc half-life.
3.5 Biokinetic Models
Two sequential modes were used to recover anatomical structures as well as radiation activity. All these images were acquired with the mice in the same position (Fig. 8). The image-processing algorithm was developed in Matlab®. The algorithm developed in this multitask software platform quantifies activity from light intensity and corrects the effect of radiation scattering, attenuation and background. This software was evaluated with three series of experiments. A set of regular quality measures were proposed to qualify the image-processing algorithm. Repeatability above 90% accuracy of less than 10 pixels proved the precision of the automatic segment algorithm.
Image analysis for both the optic and x-ray images in parallel. On the left from top to bottom, the original optic image including the highlighted target organs (a), the automatic selection of anatomic sections corresponding to the target organs (b) and the choice of ROI for the tumor region (c). On the right, the original X-ray image (d), the binary masks corresponding to the target organs (e) and the application of these masks in the selected ROIs (f). At the bottom (g), the collection of the segmented organs showing their relative activity (based on the color scale)”
Time variation of radiation activities in all the organs and tumor were evaluated in the following sampling times: 0.0, 5.0, 10.0, 15.0, 20.0, 120.0 min and 24 h (Fig. 9). These activities (normalized by the initial administrated activity) were analyzed by a nonlinear parametric identification algorithm. This algorithm produces parameters that characterize the biokinetic models of all organs and tumor (Table 2). The activity values quantified with respect to time were fitted onto a biokinetic model to the total number of disintegrations (N) of 99mTc-BN and 99mTc-RGD2 radiopharmaceuticas within each region of interest (Table 2).
4 Discussion
The image processing based modelling method presented in this study contributes to usual methods considered in the kinetic modelling of pharmaceuticals. Despite that image processing techniques used in this study has been applied by some other authors, the integrated method presented in this study considers the automatic segmentation of regions of interest that were eventually used to obtain the parameters in the kinetic model [20]. Nevertheless, the modeling strategy based on image processing depends on the specific hardware scheme used to acquire the radiopharmaceuticals activity (Xtreme, Bruker).
The processing methodology described in this study can be replicated when images are obtained with a different technology, but the results presented here can be used directly when images came from a different equipment. This seems to be the main advantage of the algorithm developed in this study.
Based on the semi-automatic image processing technique, the results presented in Table 2 can be considered less subjective than those obtained when the image segmentation is depending on the user intervention in all the stages of study. Moreover, many advanced methods such as factor analysis of dynamic structures still consider the user intervention to draw and refine the regions of interest. In the case of this study, this condition is avoided by merging the radiological and anatomical information provided by the Xtreme device.
The models obtained in this study have exponents smaller than 0.1154 which is the physical decay constant for 99mTc. Then, the faster radiation decay dynamics is governed by the proper residence times as well as accumulation activities in different organs.
When compared the data of activity quantification in kidneys observed in two preliminary studies, for both 99mTc-BN and 99mTc-RGD2, with the predicted activity by the model proposed in this study, (as result of the Student t-test), the significance of similarity study was 0.91 and 0.93 correspondingly. These values were expected considering that the animal model was evaluated under controlled conditions and therefore, the results obtained in this study requires some further experimental work in order to extrapolate its conclusions. This fact can be considered a further work that must consider less controlled conditions. Nevertheless, as a first stage, the set of experiments seems to demonstrate that the simple image processing proposed in this study can be used as part of more complex techniques. This analysis followed the strategy of comparison reported in [21] to evaluate the similarity of two independent set of experiments.
5 Conclusions
An automatic image-processing algorithm was proposed to characterize the relevant radiation activities of 99mTc-BN and 99mTc-RGD2 in target organs and breast tumor inoculated in mice. The set of images processed in this study were acquired in a multimodal preclinical imaging system known as Xtreme system. A set of quality measures were used to define the efficiency of the automatic characterization of radiation activity. Individual biokinetic models based on the radiation activity were obtained for each organ of interest. Despite the method introduced in this study was applied for modelling the accumulated activities of 99mTc-BN and 99mTc-RGD2 radiopharmaceuticals, the same methodology can be used to obtain comparable models when the radiopharmaceutical includes Tc-99m as key radiological marker.
Change history
09 February 2018
The article ���Preclinical Biokinetic Modelling of Tc-99m Radiophamaceuticals Obtained from Semi-Automatic Image Processing���, written by Luz G. Cornejo-Arag��n, Clara L. Santos-Cuevas, Blanca E. Ocampo-Garc��a, Isaac Chairez-Oria, Lorenza Diaz-Nieto, Janice Garc��a-Quiroz was originally published Online First without open access. After publication in volume [37], issue [6], page [887���898] the author decided to opt for Open Choice and to make the article an open access publication. Therefore, the copyright of the article has been changed to �� The Author(s) [2018] and the article is forthwith distributed under the terms of the Creative Commons Attribution 4.0 International License (http://creativecommons.org/licenses/by/4.0/), which permits use, duplication, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made
References
Kiessling, F., Pichler, J., & Hauff, P. (2011). Small animal imaging. Berlin: Springer.
Gross, S., & Piwnica-Worms, D. (2006). Molecular imaging strategies for drug discovery and development. Current Opinion in Chemical Biology, 10, 334–342.
Fox, J. G., Barthold, S., Davisson, M., Newcomer, C. E., Quimby, F. W., & Smith, A. (2006). The mouse in biomedical research: Diseases (Vol. 2). New York: Academic Press.
Judenhofer, M. S., Wehrl, H. F., Newport, D. F., Catana, C., Siegel, S. B., Becker, M., et al. (2008). Simultaneous PET-MRI: A new approach for functional and morphological imaging. Nature Medicine, 14, 459–465.
Cho, H., Ackerstaff, E., Carlin, S., Lupu, M. E., Wang, Y., Rizwan, A., et al. (2009). Noninvasive multimodality imaging of the tumor microenvironment: registered dynamic magnetic resonance imaging and positron emission tomography studies of a preclinical tumor model of tumor hypoxia. Neoplasia, 11(3), 247IN2–259IN3.
Cherry, S. R. (2009). Multimodality imaging: Beyond pet/ct and spect/ct. Seminars in Nuclear Medicine, 39(5), 348–353.
Doney, E., Van Avermaete, T., Chapman, S., Waldeck, J., & Leevy, W. M. (2013). Planar imaging of 99mTc labeled SPECT probes in living mice using the in-vivo Xtreme platform with radioisotopic phosphor screen. Application Note.
Ortiz-Arzate, Z., Santos-Cuevas, C. L., Ocampo-García, B. E., Ferro-Flores, G., García-Becerra, R., Estrada, G., et al. (2014). Kit preparation and biokinetics in women of 99mTc-EDDA/HYNIC-E-[c (RGDfK)] 2 for breast cancer imaging. Nuclear Medicine Communications, 35, 423–432.
Ferro-Flores, G., de Murphy, C. A., Rodrguez-Cortes, J., Pedraza-Lopez, M., & Ramrez-Iglesias, M. T. (2006). Preparation and evaluation of 99mTc-EDDA/HYNIC-[Lys3]-bombesin for imaging gastrin-releasing peptide receptor-positive tumours. Nuclear Medicine Communications, 27, 371–376.
Santos-Cuevas, C. L., Ferro-Flores, G., de Murphy, C. A., & Pichardo-Romero, P. A. (2008). Targeted imaging of gastrin-releasing peptide receptors with 99mTc-EDDA/HYNIC-[Lys3]-bombesin: biokinetics and dosimetry in women. Nuclear Medicine Communications, 29, 741–747.
Barbolosi, D., Hapdey, S., Battini, S., Faivre, C., Mancini, J., Pacak, K., et al. (2015). Determination of the unmetabolised 18F-FDG fraction by using an extension of simplified kinetic analysis method: clinical evaluation in paragangliomas. Medical & Biological Engineering & Computing, 54(1), 103–111.
Vicini, P., Brill, A. B., Stabin, M. G., & Rescigno, A. (2008). Kinetic modeling in support of radionuclide dose assessment. Seminars in Nuclear Medicine, 38(5), 335–346.
Pinard, E., Engrand, N., & Seylaz, J. (2000). Dynamic cerebral microcirculatory changes in transient forebrain ischemia in rats: Involvement of type I nitric oxide synthase. Journal of Cerebral Blood Flow & Metabolism, 20, 1648–1658.
Junk, M., Salzwedel, J., Sindlinger, T., Brkle, A., & Moreno-Villanueva, M. (2014). Mathematical modelling of the automated FADU assay for the quantification of DNA strand breaks and their repair in human peripheral mononuclear blood cells. BMC Biophysics, 7, 9.
Zaidi, H., & Erwin, W. D. (2007). Quantitative analysis in nuclear medicine imaging. Journal of Nuclear Medicine, 48, 1401.
Seletchi, E. D. (2008). Medical image processing using MATLAB. Journal of Information Systems & Operations Management, 2, 194–210.
Beekman, F. J., Kamphuis, C., & Frey, E. C. (1997). Scatter compensation methods in 3D iterative SPECT reconstruction: a simulation study. Physics in Medicine & Biology, 42, 1619.
Kim, K. M., Varrone, A., Watabe, H., Shidahara, M., Fujita, M., Innis, R. B., et al. (2003). Contribution of scatter and attenuation compensation to SPECT images of nonuniformly distributed brain activities. Journal of Nuclear Medicine, 44, 512–519.
Dodgas, B., Sattuck, D. W., & Leahy, R. M. (2005). Segmentation of skull and scalp in 3D human MRI using mathematical morphology. Human Brain Mapping, 26(4), 273–285.
Pham, D. L., Xu, C., & Prince, J. L. (2000). Current methods in medical image segmentation 1. Annual Review of Biomedical Engineering, 2, 315–337.
Jannin, P., Grova, C., & Maurer, C. R., Jr. (2006). Model for defining and reporting reference-based validation protocols in medical image processing. International Journal of Computer Assisted Radiology and Surgery, 1, 63–73.
Acknowledgements
Authors want to acknowledge the support given by the projects IPN-SIP-COFAA-2015-0344, CONACyT-CB-2013-221867 and CONACyT-PDCPN-2015-01-1040 granted by the National Polytechnic Institute and the National Council of Science and Technology, respectively. This research was carried out as part of the activities of the “Laboratorio Nacional de Investigación y Desarrollo de Radiofármacos, CONACyT”.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interests regarding the publication of this paper.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made.
The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder.
To view a copy of this licence, visit https://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Cornejo-Aragón, L.G., Santos-Cuevas, C.L., Ocampo-García, B.E. et al. Preclinical Biokinetic Modelling of Tc-99m Radiophamaceuticals Obtained from Semi-Automatic Image Processing. J. Med. Biol. Eng. 37, 887–898 (2017). https://doi.org/10.1007/s40846-017-0250-4
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40846-017-0250-4