Skip to main content
SpringerLink
Log in

A Two-Warehouse Inventory Model for Deteriorating Items with Capacity Constraints and Back-Ordering Under Financial Considerations

  • Original Paper
  • Published:
International Journal of Applied and Computational Mathematics Aims and scope Submit manuscript

Abstract

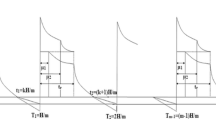
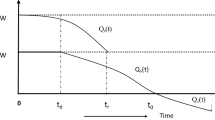
This paper investigated two warehouse inventory model for a single deteriorating items under the assumption of shortages and partial backlogging under payments delay and the effect of inflation and time value for money is also incorporated. Again, two warehouse capacity (owned and rented) have been considered over the finite horizon planning under which back-ordering is assumed. When the order quantity becomes higher than the storage capacity in own warehouse then the system involves two warehouse model. In this model, excess inventory are stored in rented warehouses which are assumed to charge higher unit holding costs than owned warehouses. Moreover, in rented warehouse item deteriorates with higher rates than in owned warehouse. At first own warehouse are filled out by its storage capacity and the rests are kept in rented warehouse. So, at first, the items in RW decreases due to demand and deterioration until it reaches to the level zero while on the other hand a portion on the inventory on OW is depleted due to deterioration only. Then, the inventory on OW decreases due to demand and deterioration until it reaches to the level zero. Finally, shortages start and backlogging rate is negative exponential of function waiting time. Here, the demand is used as exponential function of time and backlogging rate varies negative exponential function of waiting time. The total cost function is carried out under the effect of JIT setup cost. Two numerical examples are illustrated for the developed model and sensitivity analysis has been carried out to identify behaviour of model parameters.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5

Similar content being viewed by others

References

  1. Hartely, V.R.: Operations Research—A Managerial Emphasis, pp. 315–317. Santa Monica, CA (1976)

    Google Scholar 

  2. Goswami, A., Chaudhuri, K.S.: An economic order quantity model for items with two levels of storage for a linear trend in demand. J. Oper. Res. Soc. 43, 157–167 (1992)

    Article  MATH  Google Scholar 

  3. Sarma, K.V.S.: A deterministic order-level inventory model for deteriorating items with two storage facilities. Eur. J. Oper. Res. 29, 70–73 (1987)

    Article  MathSciNet  MATH  Google Scholar 

  4. Pakkala, T.P.M., Achary, K.K.: A deterministic inventory model for deteriorating items with two warehouses and finite replenishment rate. Eur. J. Oper. Res. 57, 71–76 (1992)

    Article  MATH  Google Scholar 

  5. Zhou, Y.W., Yang, S.L.: A two-warehouse inventory model for items with stock-level-dependent demand rate. Int. J. Prod. Econ. 95, 215–228 (2005)

    Article  Google Scholar 

  6. Lee, C.C.: Two-warehouse inventory model with deterioration under FIFO dispatching policy. Eur. J. Oper. Res. 174, 861–873 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  7. Yang, H.L.: Two-warehouse partial backlogging inventory models for deteriorating items under inflation. Int. J. Prod. Econ. 103, 362–370 (2006)

    Article  Google Scholar 

  8. Jaggi, C.K., Cardenas-Barron, L.E., Tiwari, S., Shafi, A.: Two-warehouse inventory model for deteriorating items with imperfect quality under the conditions of permissible delay in payments. Sci. Iran. Trans. E 24(1), 390–412 (2017)

    Google Scholar 

  9. Tiwari, S., Cardenas-Barron, L.E., Khanna, A., Jaggi, C.K.: Impact of trade credit and inflation on retailer’s ordering policies for non-instantaneous deteriorating items in a two-warehouse environment. Int. J. Prod. Econ. 176, 154–169 (2016)

    Article  Google Scholar 

  10. Sett, B.K., Sarkar, B., Goswami, A.: A two-warehouse inventory model with increasing demand and time varying deterioration. Sci. Iran. Trans. E Ind. Eng. 19, 306–310 (2012)

    Google Scholar 

  11. Shah, N.H.: A lot-size model for exponentially decaying inventory when delay in payments is permissible. Cahiers du CERO 35, 115–123 (1993)

    MATH  Google Scholar 

  12. Aggarwal, S.P., Jaggi, C.K.: Ordering policies of deteriorating items under permissible delay in payments. J. Oper. Res. Soc. 46, 658–662 (1995)

    Article  MATH  Google Scholar 

  13. Jamal, A.M.M., Sarker, B.R., Wang, S.: An ordering policy for deteriorating items with allowable shortages and permissible delay in payment. J. Oper. Res. Soc. 48, 826–833 (1997)

    Article  MATH  Google Scholar 

  14. Sarkar, B.: An EOQ model with delay-in-payments and time-varying deterioration rate. Math. Comput. Model. 55, 367–377 (2012)

    Article  MathSciNet  MATH  Google Scholar 

  15. Chung, K.J., Liao, J.J.: Lot-sizing decisions under trade credit depending on the ordering quantity. Comput. Oper. Res. 31, 909–928 (2004)

    Article  MATH  Google Scholar 

  16. Chung, K.J., Liao, J.J.: The optimal ordering policy in a DCF analysis for deteriorating items under trade credit depending on the ordering quantity. Int. J. Prod. Econ. 100, 116–130 (2006)

    Article  Google Scholar 

  17. Shinn, S.W., Hwang, H.: Optimal pricing and ordering policies for retailers under order-size-dependent delay in payment. Comput. Oper. Res. 30, 35–50 (2003)

    Article  MATH  Google Scholar 

  18. Huang, K.N., Liao, J.J.: A simple method to locate the optimal solution for exponentially deteriorating items under trade credit financing. Comput. Math. Appl. 56, 965–977 (2008)

    Article  MathSciNet  MATH  Google Scholar 

  19. Liao, J.J.: On an EPQ model for deteriorating items under permissible delay in payments. Appl. Math. Model. 31, 393–403 (2007)

    Article  MATH  Google Scholar 

  20. Liao, J.J.: A note on an EOQ model for deteriorating items under supplier credit linked to ordering quantity. Appl. Math. Model. 31, 1690–1699 (2007)

    Article  MATH  Google Scholar 

  21. Chen, S.-C., Cardenas-Barron, L.E., Teng, J.T.: Retailer’s economic order quantity when the supplier offers conditionally permissible delay in payments link to order quantity. Int. J. Prod. Econ. 155, 284–291 (2014)

    Article  Google Scholar 

  22. Ghare, P.M., Schrader, G.P.: A model for an exponentially decaying inventory. J. Ind. Eng. 14, 238–243 (1963)

    Google Scholar 

  23. Covert, R.P., Philip, G.P.: An EOQ model for items with Weibull distribution deterioration. Am. Inst. Ind. Eng. Trans. 5, 323–326 (1973)

    Google Scholar 

  24. Cheng, M., Zhang, B., Wang, G.: Optimal policy for deteriorating items with trapezoidal type demand and partial backlogging. Appl. Math. Model. 35, 3552–3560 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  25. Chung, K.J., Lin, S.D.: The inventory model for trade credit in economic ordering policies of deteriorating items in a supply chain system. Appl. Math. Model. 35, 3111–3115 (2011)

    Article  MathSciNet  MATH  Google Scholar 

  26. Cardenas-Barron, L.E.: The economic production quantity (EPQ) with shortage derived algebraically. Int. J. Prod. Econ. 70, 289–292 (2011)

    Article  Google Scholar 

  27. Widyadana, G.A., Cardenas-Barron, L.E., Wee, H.M.: Economic order quantity model for deteriorating items and planned back-order level. Math. Comput. Model 54, 1569–1575 (2011)

    Article  MATH  Google Scholar 

  28. Chung, C.J., Widyadana, G.A., Wee, H.M.: Economic production quantity model for deteriorating inventory with random machine unavailability and shortage. Int. J. Prod. Res. 49, 883–902 (2011)

    Article  MATH  Google Scholar 

  29. Sarkar, M., Sarkar, B.: An economic manufacturing quantity model with probabilistic deterioration in a production system. Econ. Model. 31, 245–252 (2013)

    Article  Google Scholar 

  30. Sarkar, B., Sarkar, S.: Variable deterioration and demand—an inventory model. Econ. Model. 31, 548–556 (2013)

    Article  Google Scholar 

  31. Sarkar, B., Saren, S., Wee, H.M.: An inventory model with variable demand, component cost and selling price for deteriorating items. Econ. Model. 30, 306–310 (2013)

    Article  Google Scholar 

  32. Sarkar, B.: A production-inventory model with probabilistic deterioration in two-echelon supply chain management. Appl. Math. Model. 37, 3138–3151 (2013)

    Article  MathSciNet  MATH  Google Scholar 

  33. Sarkar, B., Saren, S., Cardenas-Barron, L.E.: An inventory model with trade-credit policy and variable deterioration for fixed lifetime products. Ann. Oper. Res. 229(1), 677–702 (2016)

    Article  MathSciNet  MATH  Google Scholar 

  34. Sarkar, B., Mandal, B., Sarkar, S.: Preservation of deteriorating seasonal products with stock-dependent consumption rate and shortages. J. Ind. Manag. Optim. 13(1), 187–206 (2017). https://doi.org/10.3934/jimo.2016011

    MathSciNet  MATH  Google Scholar 

  35. Wu, J., Al-khateeb, F.B., Teng, J.T., Cardenas-Barron, L.E.: Inventory models for deteriorating items with maximum lifetime under downstream partial trade credits to credit-risk customers by discounted cash-flow analysis. Int. J. Prod. Econ. 171, 105 (part 1)–115 (2016)

    Article  Google Scholar 

  36. Sarkar, B., Saren, S., Cardenas-Barron, L.E.: An inventory model with trade-credit policy and variable deterioration for fixed lifetime products. Ann. Oper. Res. 229(1), 677–702 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  37. Shah, N.H., Cardenas-Barron, L.E.: Retailer’s decision for ordering and credit policies for deteriorating items when a supplier offers order-linked credit period or cash discount. Appl. Math. Comput. 259, 569–578 (2015)

    MathSciNet  Google Scholar 

  38. Ray, J., Chaudhuri, K.S.: An EOQ model with stock-dependent demand, shortage, inflation and time-discounting. Int. J. Prod. Econ. 53, 171–180 (1997)

    Article  Google Scholar 

  39. Chen, J.M.: An inventory model for deteriorating items with time-proportional demand and shortages under inflation and time discounting. Int. J. Prod. Econ. 55, 21–30 (1998)

    Article  Google Scholar 

  40. Bose, S., Goswami, A., Chaudhuri, K.S.: An EOQ model for deteriorating items with linear time-dependent demand rate and shortages under inflation and time discounting. J. Oper. Res. Soc. 46, 771–782 (1995)

    Article  MATH  Google Scholar 

  41. Sarkar, B., Sana, S.S., Chaudhuri, K.S.: A finite replenishment model with increasing demand under inflation. Int. J. Math. Oper. Res. 2(3), 347–385 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  42. Roy, T., Chaudhuri, K.S.: A finite time-horizon deterministic EOQ model with stock level-dependent demand, effect of inflation and time value of money with shortage in all cycles. Yugosl. J. Oper. Res. 17(2), 195–207 (2007)

    Article  MathSciNet  MATH  Google Scholar 

  43. Sana, S.S.: A production-inventory model in an imperfect production process. Eur. J. Oper. Res. 200, 451–464 (2010)

    Article  MathSciNet  MATH  Google Scholar 

  44. Roy, T., Chaudhuri, K.S.: A finite time horizon EOQ model with ramp-type demand rate under inflation and time-discounting. Int. J. Oper. Res. 11(1), 100–118 (2011). Kindly check and confirm the inserted page range is correctly identified for the reference [44]

    Article  MathSciNet  MATH  Google Scholar 

  45. Ouyang, L.-Y., Yang, C.-T., Chan, Y.L., Cardenas-Barron, L.E.: A comprehensive extension of the optimal replenishment decisions under two levels of trade credit policy depending on the order quantity. Appl. Math. Comput. 224, 268–277 (2013)

    MathSciNet  MATH  Google Scholar 

  46. Wu, J., Ouyang, L.Y., Cardenas-Barron, L.E., Goyal, S.K.: Optimal credit period and lot size for deteriorating items with expiration dates under two-level trade credit financing. Eur. J. Oper. Res. 237(3), 898–908 (2014)

    Article  MathSciNet  MATH  Google Scholar 

  47. Chung, K.J., Cardenas-Barron, L.E., Ting, P.S.: An inventory model with non-instantaneous receipt and exponentially deteriorating items for an integrated three layer supply chain system under two levels of trade credit. Int. J. Prod. Econ. 155, 310–317 (2014)

    Article  Google Scholar 

  48. Yang, H.H.: Two-warehouse inventory models for deteriorating items with shortages under inflation. Eur. J. Oper. Res. 157, 344–356 (2004)

    Article  MathSciNet  MATH  Google Scholar 

  49. Hou, K.L.: An inventory model for deteriorating items with stock-dependent consumption rate and shortages under inflation and time discounting. Eur. J. Oper. Res. 168, 463–474 (2006)

    Article  MathSciNet  MATH  Google Scholar 

  50. Cardenas-Barron, L.E., Chung, K.J., Trevio-Garza, G.: Celebrating a century of the economic order quantity model in honor of Ford Whitman Harris. Int. J. Prod. Econ. 155, 1–7 (2014). (2006)

    Article  Google Scholar 

  51. Liao, J.J., Huang, K.N.: Deterministic inventory model for deteriorating items with trade credit financing and capacity constraints. Comput. Ind. Eng. 59, 611–618 (2010)

    Article  Google Scholar 

  52. Sarkar, B., Saren, S.: Product inspection policy for an imperfect production system with inspection errors and warranty cost. Eur. J. Oper. Res. 248, 263–271 (2016)

    Article  MATH  Google Scholar 

  53. Sarkar, B.: Supply chain coordination with variable back order, inspections, and discount policy for fixed lifetime products. Math. Prob. Eng. 2016, 14 (2016). https://doi.org/10.1155/2016/6318737

    Article  Google Scholar 

  54. Sarkar, B., Sarkar, S., Yun, W.Y.: Retailer’s optimal strategy for fixed lifetime products. Int. J. Mach. Learn. Cybern. 7, 121–133 (2016)

    Article  Google Scholar 

  55. Tripathi, R.P., Chaudhary, S.K.: Inflationary induced EOQ model for Weibull distribution deterioration and trade credits. Int. J. Appl. Comput. Math. 3, 3341–3353 (2017). https://doi.org/10.1007/s40819-016-0298-9

    Article  MathSciNet  Google Scholar 

  56. Das, P., De, S.K., Sana, S.S.: An EOQ model for time dependent backlogging over idle time: a step order fuzzy approach. Int. J. Appl. Comput. Math. 1(2), 171–185 (2015)

    Article  MathSciNet  MATH  Google Scholar 

  57. Sarkar, B., Sana, S.S., Chaudhuri, K.S.: An Economic production quantity model with stochastic demand in an imperfect production system. Int. J. Serv. Oper. Manag. 9(3), 259–283 (2011)

    Google Scholar 

Download references

Acknowledgements

The authors wish to thank the anonymous referees for their helpful comments and suggestions which greatly improved the content of the article.

Author information

Authors and Affiliations

  1. Department of Mathematics, Vidyasagar College for Women, 39, Sankar Ghosh Lane, Kolkata, 700006, India

    R. Chakrabarty & T. Roy

  2. Department of Mathematics, Jadavpur University, Kolkata, 700032, India

    K. S. Chaudhuri

Authors
  1. R. Chakrabarty
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. T. Roy
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. K. S. Chaudhuri
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to R. Chakrabarty.

Appendix A

Appendix A

From Eq. (3) we obtain order quantity \(Q=I(0)=\frac{a}{\alpha + b}(e^{(\alpha + b)t_{1}}-1)\) and if the order quantity \(Q\le W\) then it is unnecessary to rent any warehouse. Thus \(\frac{a}{\alpha + b}(e^{(\alpha + b)t_{1}}-1)\le W\) implies \(t_{1} \le \frac{1}{\alpha + b}log(1+\frac{(\alpha + b)W }{a})\). For simplicity, let \(t_{a}=\frac{1}{\alpha + b}log(1+\frac{(\alpha + b)W }{a})\). The inequality \(Q\le W\) holds if and only if \(t_{a}\ge t_{1}\). Therefore, the inequality \(Q>W\) holds if and only if \(t_{a}< t_{1}\) which implies that there are W units of items stored in OW and the remainder are despatched in RW.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Chakrabarty, R., Roy, T. & Chaudhuri, K.S. A Two-Warehouse Inventory Model for Deteriorating Items with Capacity Constraints and Back-Ordering Under Financial Considerations. Int. J. Appl. Comput. Math 4, 58 (2018). https://doi.org/10.1007/s40819-018-0490-1

Download citation

  • Published:

  • DOI: https://doi.org/10.1007/s40819-018-0490-1

Keywords

Search

Navigation