Introduction

Gone are the days when public forest lands were managed solely for timber. Today, public forest lands are managed for a wide range of services that include timber, habitat quality, carbon, and water quality. There has been a paradigm shift from economic criteria based on timber production to one that is based on ecosystem services. Most public land management organizations make it a requirement that forest management plans provide for sustainable management of forest resources and other values. This complicates the decision-making environment of the resource manager, economically, socially, and environmentally as there are too many important societal needs to consider. If these societal needs can be quantified using decision variables, then optimization techniques can be employed to sort through all the management alternatives available to the resource manager.

Most of the decisions in forest management are carried out at either the stand level or at the forest level. A typical stand-level management problem deals with determining the time and intensity to implement each treatment in order to optimize the management objective [1]. The ability to evaluate alternative treatments for a forest stand is a fundamental step in forest management planning. Stand-level optimization is important for sorting through the alternative treatment options available to the resource manager and assisting the manager in the decision-making process. Decisions made at the stand level can be useful for the development of alternatives for forest level plans. At the forest level, the goal is to seek the best combinations of these development paths for the stands that make up the forest, taking into account the constraints and objectives for the forest as a whole.

The objective of stand-level optimization may be to produce the best management plan for each forest stand, independent of other stands in the forest. The planning process involves analyzing a number of intermediate treatments (e.g., thinning) as well as a final harvest decision. The planning process also involves finding the best timing and intensity of the silvicultural activities or finding the best stand structure that should remain after the activities. Although decisions made at the stand level can be useful for the development of alternatives for forest level problems, the decisions are not impacted by decisions assigned to other stands, nor by the condition of the surrounding forests [2]. This is because combining an optimal solution from each forest stand may not be optimal under the consideration of forest level constraints. But it is important to note that some inferior solutions at the stand level could improve the solution at the forest level.

A number of techniques have been proposed or applied to solve stand-level optimization problems. These techniques can come in handy when a forest manager is faced with a large number of choices for which a manual decision is impossible. The emergence of operations research and computer science in the past few decades have provided powerful tools for solving stand-level optimization problems. The first known application of operations research technique in forest stand-level planning was the work by Arimizu [3], with input from the founders of dynamic programing (DP), Bellman and Dreyfus. Since the publication of his work appeared in the 1957 issue of Journal of Operations Research Society of Japan, his accomplishment was overlooked for several years by many in the scientific community.

In this paper, we present an overview of the methodologies used in stand-level optimization. We analyze the strengths and weaknesses of these methodologies as well as provide comments on the effectiveness of the methodology under consideration. We then dig deeper into dynamic programing approach for generalizing solution specification and techniques.

Review of Methodologies

A classic stand-level optimization problem in forest economics involves the use of “derivatives” to determine the harvest age for an even-aged forest stand which maximizes the net present value of an infinite series of timber regeneration, growth, and harvest cycles. Faustmann [4] is usually attributed with the first appropriate solution to this problem when only timber values are considered given that there is no stochasticity in all elements. Samuelson [5] provides a more formal mathematical specification of the problem. Hartman [6] extends the model to include values associated with standing trees (e.g., wildlife habitat) as well as the extractive value of timber harvest. With stochasticity, however, the Faustmann formulation could lead to a false optimal solution [7, 8]. Additionally, the ceasing or giving-up phenomena of the management activities cannot be captured by the Faustmann formulation due to the underlying assumptions of sustainability, i.e., assumption of a continuous plantation-harvest behavior over time. When considering these phenomena, stochastic control modeling approach such as stochastic dynamic programming plays an important role in solving the management problem [9].

Several authors have also used optimal control theory in stand-level optimization. This approach has been shown by Heaps [10] to converge to the Faustmann model in the steady state. Some of these papers directly address the incorporation of Faustmann models into market analyses (e.g., [11, 12]). Anderson [13] developed an optimal control approach to a timber management problem that included the opportunity cost of forested land. His generalized steady-state control solution was shown to be identical to the Faustmann rotation model. Optimal control theory is used to derive a set of necessary conditions for control in Hamiltonian under maximum (or minimum) principle by relying on differentiability of the problem setting. The approach can differ from the classical calculus of variations when it uses control variables to optimize the function.

Optimal control theory may be the most appropriate to formulate the stand-level planning problem from the viewpoint of mathematical economics in order to provide insights of economic or practical conditions for optimal solution. However, because of the growing complexity in stand-level optimization problems, many other practical methods which specify planning regime over time have been proposed. These optimum seeking methods are major applications of mathematical programming techniques in the field of operations research. Table 1 shows a chronological list of researchers who have used mathematical programming techniques in forest stand-level planning. Among the different derivative-free solution techniques used in stand-level optimization, non-linear programming (NLP) methods have been employed the most. This is primarily due to the attribute of the growth models and the discrete nature of the dynamics. These derivative-free solution techniques have been grouped into several broad categories by various authors. Valsta [14] classified stand-level optimization solution techniques into deterministic and stochastic methods. He defined the deterministic methods to include the following: DP, optimal control theory, NLP, and random search. The definition was based on the fact that the decision variables and constraints do not contain stochasticity. He then grouped the stochastic methods into the following: adaptation and anticipation methods, stochastic DP and optimal stopping, and stochastic non-linear programming. Bettinger et al. [15] grouped the solution techniques into four broad categories: Hooke and Jeeves [16], heuristics and meta models, NLP, and DP. Later in 2010, Bettinger et al. [2] further reclassified these solution techniques into three broad categories: Hooke and Jeeves (NLP), heuristics or meta models, and DP.

Table 1 Change in optimization approach over years
Full size table

In this paper, the focus is on deterministic techniques for forest stand-level planning as shown by the summarized literature in Table 1. For stochastic techniques, we would like to refer the readers of this paper to Bettinger [17] who investigated stochastic techniques related to wildfire and forest planning. We would also like to direct interested readers to Yousefpour et al. [9] who reviewed techniques for modeling climate change under the scheme of adaptive forest management. Other papers that addressed stochasticity or risk and uncertainty, in a DP framework include the following: Gunn [18], Díaz-balteiro and Rodriguez [19], Zhou and Buongiorno [20]; Ferreira et al. [21] and Ferreira et al. [22]; Yoshimoto and Shoji [23]; Yoshimoto [24]. In this study, we use deterministic solution techniques to describe a situation where the future state of a forest stand can be predicted exactly from knowledge of the present and all inputs and events are assumed to be known with certainty. The rest of the “Review of Methodologies” section describes the different approaches for solving forest stand-level optimization problems. We analyze the strengths and weakness of these approaches, as well as reveal the conditions under which one approach would be preferred over the other. Generally, there is no one single algorithm that is suitable for all optimization problems. However, in the “General Formulation of Forest Stand-Level Planning Problem” section of this manuscript, we will propose the most appropriate approach for any given problem, within the DP framework.

Non-linear Programming (NLP) Approach

Non-linear programming (NLP) is a method used to optimize a problem with a non-linear objective function subject to non-linear constraints. Since most growth and yield models are constructed in a non-linear framework, NLP may be ideal for solving problems of forest stand-level planning. A wide variety of NLP techniques have been proposed in operations research field. Among them, a derivative-free method is suitable for forestry problems due to discreteness and non-differentiability of growth models with respect to management activities including thinning and harvesting. The Hooke and Jeeves method is the one most often applied in forest stand-level planning. This technique is very popular because it is easy to use and can perform well with discreteness of growth models on the expected concavity of the response surface. The Hooke and Jeeves method is described as a “direct search method”, which involves a sequential examination of the changes that occur when a problem is solved and the results are compared to the “best” solution among the derived candidate solutions, together with a strategy for determining the next trial solution, based on previously obtained results. This solution technique is very similar to modern day heuristic techniques, except that many heuristics contain provisions that allow the search process to deviate in a negative direction from the best solution stored in memory, with the purpose of exploring larger areas of the solution space.

The Hooke and Jeeves method has a long history in forestry [25–33]. Generally, the Hooke-Jeeves algorithm consists of two major phases: an “exploratory search” around the base point and a “pattern search” in a direction selected for optimization (minimization or maximization) [16]. The exploratory move is performed in the vicinity of the current point systematically to find the best point around the current point. Thereafter, two points are used to make a pattern move. It is important to note that if the gradient information is available, a gradient-based method may be another option worth considering.

The Hooke and Jeeves method is comparable to other techniques in terms of solution time. Roise [34] made a comparison of three different NLP techniques and discrete DP. He measured relative efficiency in finding a solution in terms of the amount of central processing unit and concluded that the Hooke and Jeeves method is not significantly superior to DP. In a similar study, Pukkala [35] concluded that the Hooke and Jeeves method is faster in terms of computing time than any of the population-based methods considered in his study. However, Yoshimoto et al. [36] pointed out that the main shortcoming of NLP techniques such as the Hooke and Jeeves method, for determination of the optimal is the non-concave production or response surface derived from the target growth model with respect to the decision variable to seek a final solution. The result of this is the inability to find a “global” optimum. In other words, searching results could end in the vicinity of local optima due to local concavity of the growth model behavior. NLP methods can be efficient and effective if the response surface to seek an optimal solution has the property of concavity for maximization or convexity for minimization. Note that during the search process by NLP methods, it would be difficult to investigate how the response surface is formed. In other words, a set of derived candidate solutions as well as intermediate solutions is not enough to investigate if the response surface is concave.

NLP has also been used in uneven-aged management. Tahvonen et al. [37] used data from long-term experiments of uneven-aged forest to develop a transition matrix growth model [38] for a Norway spruce stand and formulated a NLP problem searching for the optimal management. Tahvonen [39] extended the study by Tahvonen et al. [37] and applied a more detailed single tree growth model rather than transition matrix model to an uneven-aged Norway spruce stand. Pukkala et al. [40] optimized a mixed forest stand with pine, spruce, and birch in Finland using the Hooke and Jeeves method without specific optimization formulation.

Heuristics Technique or Meta Models

There are many stand-level problems or growth models that are too complex to be solved by the existing optimization techniques within a reasonable timeframe, even with the help of modern computers. These types of problems are most often handled by using heuristic techniques in forestry. Note that heuristics have been traditionally employed in forest planning at the forest level, when the decision variables are binary. With the exception of genetic algorithms, most heuristics follow a local improvement methodology. The solution is improved gradually by changing it locally.

Bullard et al. [41] may be the first to develop the heuristic random search algorithm to simultaneously estimate optimal thinning and the final harvest age. The model was formulated using a stand-table projection growth model in a non-linear-integer programming framework, to predict mixed-species growth and stand structure. After the introduction of the major heuristic algorithms such as simulated annealing [42] and tabu search [43] in the 1980s, several researchers have incorporated these algorithms into forest stand-level optimization problems, though most of the application have been found in forest-level harvest scheduling optimization. A genetic algorithm was applied in Chikumbo and Nicholas [44], while Eriksson [45] used simulated annealing in addition to NLP with the gradient method. Tabu search was also used in Wikström [46]. The main concern with these techniques is that the final or “optimal” solution generally does not have optimal attributes but is guaranteed to be the “best” among the generated group of solutions. They give us at least a feasible and hopefully “near-optimal” solution. Heuristics can be described as trial-and-error techniques that seek a final solution without being able to guarantee an optimal solution [47]. They are designed to explore larger areas of the solution space randomly or with semi-random sequences deterministically. Heuristics are popular because of their flexibility and ease to implement in programming. Some heuristic techniques are deterministic: from the same initial solution, they always return the same final solution. Others are stochastic (e.g., simulated annealing, tabu search, threshold accepting, genetic algorithms), which means that from the same initial solution, they may return a different final solution due to the random characteristics of their search processes.

Although heuristics are generally simple to build and require only modest programming skills, they must be modified to fit each planning problem. There is no universal algorithm for all problems. Another concern, as outlined earlier, stems from the quality of the solution produced, i.e., no guarantee for locating an optimal solution. The advantage of heuristics is mainly due to the quickness of generating very good and feasible solutions to complex problems, once the heuristic is developed appropriately. Previous research including Bettinger et al. [48] and Pukkala and Miina [31] have shown in forest management that quality solutions can be obtained using heuristics. If the quality of the solution is deemed high compared to exact solution techniques, then heuristics are the preferred solution technique.

Dynamic Programming (DP) Approach

Dynamic programming, unlike NLP only requires one starting point for an iterative search. Once the DP network is “appropriately” constructed for the target problem, Bellman’s principle of optimality works to seek an optimal solution. That is, construction of the DP network is the most important task for DP application. Bellman’s principle of optimality states that “An optimal policy has the property that whatever the initial state and initial decision, the remaining decisions must constitute an optimal policy with regard to the state resulting from the first decision.” Put in another way, it means that given the current state, there exists an optimal policy for a sub-problem from the current state to the final state of the final stage regardless of the initial state and decision, which consists of further local optimal policies between two sequential stages connecting from the current state. Thus, the current state can be a part of the final optimal policy, but not necessarily. It is this property that allows DPs to be broken up into a series of smaller, simpler sub-problems, and there always exists an optimal policy from each state to the final state of the final stage. DP allows one to examine a large number of alternatives by reducing the range of options examined and by thoroughly searching the solution space. DP is a powerful approach to stand-level optimization problems because growth models are dynamic in nature.

After the introduction of DP by Bellman [49], the first application of DP in forestry was conducted by Arimizu [3] for an optimal thinning regime in the USA. DP allows one to solve many different types of sequential optimization problems in a reasonable timeframe. It is a recursive optimization approach that simplifies complex problems by transforming them into a DP network with a sequence of smaller simpler problems [50].

DP has been used extensively in forest management for several decades. Earlier applications revolved around the use of DP to find the optimal scheduling of silvicultural treatments or timber management in even-aged stands within the “classical” framework [51–53], including the use of DP for intermediate treatments and optimal forest rotations [54–59]. Schreuder [60] solved an optimal thinning and rotation age problem using DP. Assuming continuous time, he formulated the problem in the form of calculus of variation but could not get a close form solution. When he recast the same problem in DP form, he was able to get a numerical solution. Brodie et al. [54] employed forward recursion and developed a method to find the optimal thinning schedule and rotation length. They concluded that forward recursion is more flexible for thinning analysis. One drawback in their study was the fact that they did not consider more intensive thinnings to speed up diameter growth. This problem was solved by Brodie and Kao [61] who used a biometric model instead of a yield table and developed a DP model. Other similar studies include the works by Kao and Brodie [55], Riitter et al. [56], Chen et al. [62], Brodie, and Haight [63]. Integration of DP and stand growth and yield models has allowed the simultaneous determination of the timing and intensity of thinnings. Successful integration of the two requires that one limits the number of variables used to define thinning decisions [57].

As the target growth model becomes more complicated for precise description of growth phenomena, constructing the DP network by the classical framework begins to require more dimensions for the state descriptors over stage defined by time. In other words, the DP network is constructed by defining the main elements of growth simulator for the state descriptors. As a result, encompassing a higher number of main elements increases the introduction of state descriptors into the DP network, which results in the curse of dimensionality [64]. A major breakthrough to overcome the curse of dimensionality using a classical DP framework was employed by Paredes and Brodie [65], who introduced an efficient DP algorithm called PATH (Projection Alternative TecHnique). They constructed a DP thinning model with a whole stand growth model. This algorithm reduces the scheduling problem to a “one-state and one-stage” DP problem regardless of the number of the main elements for the growth simulator. Yoshimoto et al. [66] advanced scientific knowledge in this area by introducing MSPATH (Multi-Stage PATH) algorithm to incorporate all possible “look-aheads” in the optimization instead of the one-stage “look-ahead” of the algorithm PATH. Two years later, Yoshimoto et al. [36] introduced RLS-PATH (Region Limiting Strategies PATH) for the multivariate control problem. The advantage of this algorithm stems from the ability of DP approaches to avoid including multiple partial local optima in the solution. This algorithm has been successfully employed by Bettinger et al. [15] in density-dependent forest stand-level optimization as well as by Graetz et al. [67].

Although DP has been used extensively in even-aged stand-level optimization problems, for computational reason within the classical framework, it has generally not been used to optimize uneven-aged management decisions. This has primarily been the results of large state space [68]. Anderson and Bare [68] used deterministic DP formulation that maximizes net present value of harvested trees at each stage, to show that DP provides a promising approach to analyzing uneven-aged stand management problems. In their model, state variables were described by the number of trees and total basal area per hectare as is the case in the classical framework. Uneven-aged stand management decisions have a long history in forestry, including early works by Duerr and Bond [69], Adams and Ek [70], Buongiorno and Mitchie [71], and Chang [72]. Recent interest in uneven-aged management has attracted a considerable amount of deterministic optimization studies especially in Europe, where even-aged stand management has been dominantly implemented [73]. Ribeiro et al. [74] applied DP by MSPATH in the uneven-aged and distance-dependent model for cork oak forests in Portugal without heavy computational burden.

DP also offers the flexibility for addressing various types of spatial considerations involving stand neighborhoods [75]. DP models can be used to schedule core area production over time as well as satisfy adjacency constraints. Hoganson et al. [76, 77] have tracked and valued core area in forest management scheduling models based on DP. More recently, DP has been used in some papers as an approach to stand-level optimization with respect to non-timber values such as carbon sequestration. Diaz-Balteiro and Rodriguez [78] considered carbon payments in their analysis of optimal coppice management strategies for fast-growing species in Brazil and Spain using a DP technique within the classical framework. Other researchers such as Yoshimoto and Marušák [79], optimized timber and carbon values in a forest stand using DP by MSPATH where both thinnings and final harvest were considered. Asante et al. [80] and Asante and Armstrong [81] also used DP to determine the optimal harvest decision for a forest stand in the boreal forest of western Canada that provides both timber harvest volume and carbon sequestration services without considering the intermediate treatment such as thinning.

General Formulation of Forest Stand-Level Planning Problem

When the dynamics of growth is considered, it is natural to consider dynamic optimization approaches such as DP. In this section, we generalize the forest stand-level planning problem by the formulation of the common dynamic optimization and propose a solution approach by DP within the one-state and one-stage framework.

Let us introduce a vector of time-varying state variables, x(t) describing the state of forest stand and a vector of control variables, u(t) of thinning affecting the growth of a forest stand at time t. All required input components for the growth model could be handled by x(t) and u(t). Introducing an instant performance index or net present value functional, \( \dot{I}\left(\mathbf{x}(t),\mathbf{u}(t)\right) \), from the current state of forest stand over the small interval of time as a function of the state vector and the control vector. The objective is to seek an optimal control or management regime to maximize its summation of the integral from time t 0 to time t n .

$$ \begin{array}{l}\underset{\left\{\mathbf{u}(t)\right\}}{ \max}\kern0.5em J={\displaystyle {\int}_{t_0}^{t_n}\dot{I}\left(\mathbf{x}(t),\mathbf{u}(t)\right)dt}\hfill \\ {}\mathrm{subject}\ \mathrm{t}\mathrm{o}\hfill \\ {}\kern1.6em \dot{\mathbf{x}}(t)\kern-1.3em =\kern-1.3em f\kern-1.1em \left(\mathbf{x}(t),\mathbf{u}(t)\right)\hfill \\ {}\kern1.7em \mathbf{x}\kern-3.7em \left({t}_0\right)\kern-4em =\kern-4em {\mathbf{x}}_0\hfill \end{array} $$
(1)

where f(⋅) is assumed to be continuously differentiable function of (x(t), u(t)) to describe a dynamic change of the state, x(t) over small interval of time. Equation (1) is one of the typical formulations of the continuous time optimal control formulation with a dynamic change of the state by \( \dot{\mathbf{x}}(t) \) from the initial state of x 0.

Let us consider discrete thinning activities over time, with final harvesting to maximize the net present value of the total profit from these activities. Converting the above continuous problem into a discrete thinning problem will result in the following objective function:

$$ \begin{array}{ll}\underset{\left\{\mathbf{u}\left({t}_i\right)\right\}}{ \max}\hfill & J\kern-2.9em =\kern-3.8em {\displaystyle \sum_{i=0}^{n-1}{\displaystyle {\int}_{t_i}^{t_{i+1}}\kern-0.25em \dot{I}\left(\mathbf{x}(t),\mathbf{u}(t)\right)dt}}\hfill \\ {}\hfill & \kern2.1em ={\displaystyle \sum_{i=0}^{n-1}\left\{I\left(\mathbf{x}\left({t}_{i+1}\right)|\mathbf{x}\left({t}_i\right),\mathbf{u}\left({t}_i\right)\right)-I\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_i\right),\mathbf{u}\left({t}_i\right)\right)\right\}}\hfill \end{array} $$
(2)

given that thinning control, u(t i ) at time t i only affects the state of forest stand, x(t i + 1) at time t i + 1. Discrete dynamics of the state is expressed by a function g(⋅) of (x(t), u(t)) over the given time interval from t i to t i + 1:

$$ \mathbf{x}\left({t}_{i+1}\right)=g\left(\mathbf{x}\left({t}_i\right),\mathbf{u}\left({t}_i\right)\right) $$
(3)

Note that I(x(t i + 1)| x(t i ), u(t i )) is the net present value of profit from a forest stand at time t i + 1 after having thinning control, u(t i ) at time t i but before any control at time t i + 1. Thus, by setting I(u(t i )) equal to the net present value of profit from thinning control, u(t i ) itself such as that from thinned trees, the second term of the right-hand side of Eq. (2) becomes:

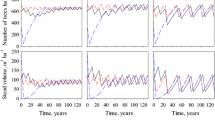
$$ I\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_i\right),\mathbf{u}\left({t}_i\right)\right)=I\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_{i-1}\right),\mathbf{u}\left({t}_{i-1}\right)\right)-I\left(\mathbf{u}\left({t}_i\right)\right) $$
(4)

That is, I(x(t i )| x(t i ), u(t i )) is the net present value of profit from a forest stand at time t i just before having thinning control, u(t i ) at time t i . Figure 1 depicts examples of trajectory of I(⋅) with thinning control over time. Figure 1a represents the case for considering volume of a forest stand, while Fig. 1b represents some value of a forest stand considering other factors such as biodiversity, esthetic value, and ecosystem services.

Fig. 1
figure 1

Examples of trajectory of net present value functional. a Volume of a forest stand. b Biodiversity, esthetic value, and ecosystem services

Full size image

As a result, Eq. (2) becomes:

$$ \begin{array}{ll}\underset{\left\{\mathbf{u}\left({t}_0\right),\dots, \mathbf{u}\left({t}_{n-1}\right)\right\}}{ \max}\kern1em J& ={\displaystyle \sum_{i=0}^{n-1}\left\{I\left(\mathbf{x}\left({t}_{i+1}\right)|\mathbf{x}\left({t}_i\right),\mathbf{u}\left({t}_i\right)\right)-I\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_i\right),\mathbf{u}\left({t}_i\right)\right)\right\}}\\ {}\kern1em & ={\displaystyle \sum_{i=0}^{n-1}\left\{I\left(\mathbf{x}\left({t}_{i+1}\right)|\mathbf{x}\left({t}_i\right),\mathbf{u}\left({t}_i\right)\right)+I\left(\mathbf{u}\left({t}_i\right)\right)-I\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_{i-1}\right),\mathbf{u}\left({t}_{i-1}\right)\right)\right\}}\kern1em \end{array} $$
(5)

Note that when i = 1 in the above summation, we replace I(x(t 0)| x(t −1), u(t −1)) by I(x(t 0)) as the initial state.

Within the one-state and one-stage framework for DP optimization, the optimality equation thus becomes

$$ \begin{array}{l}{f}_i^{*}=\underset{\left\{\mathbf{u}\left({t}_i\right)\right\}}{ \max}\left\{{f}_i\right(\mathbf{u}\left({t}_i\right)\Big\}\hfill \\ {}{f}_i\left(\mathbf{u}\left({t}_i\right)\right)={I}_i+{I}_i^u+\left\{{f}_{i-1}^{*}-{I}_{i-1}^{*}\right\}\hfill \end{array} $$
(6)

where I i  = I(x(t i + 1)| x(t i ), u(t i )), \( {I}_i^u=I\left(\mathbf{u}\left({t}_i\right)\right) \), \( {I}_i^{*}=I\left({\mathbf{x}}^{*}\left({t}_{i+1}\right)|\mathbf{x}\left({t}_i\right),{\mathbf{u}}^{*}\left({t}_i\right)\right) \), and u * (t i ) is the derived optimal thinning control at time t i for x *(t i + 1) = g(x(t i ), u *(t i )). The resultant optimal objective value becomes:

$$ {f}_n^{*}={I}_n^{*}+{I}_{n-1}^{u*}+{I}_{n-2}^{u*}\cdots +{I}_0^{u*} $$
(7)

where \( {I}_i^{u*}={I}_i^u\left({\mathbf{u}}^{*}\left({t}_{i-1}\right)\right) \). This is the optimality equation for the case of no dependency of the thinning control over multiple periods or stages. In other words, if the current thinning control only affects the thinning control at the following period, Eq. (7) becomes valid, which is the case of PATH algorithm, i.e., one-stage look-ahead. Applications of DP to thinning optimization using the classical framework can be regarded as one-stage look-ahead just like the PATH network, since thinning at each period is assumed to be independent of each other over multiple periods. The DP network of this is depicted by Fig. 2a.

Fig. 2
figure 2

DP network within the “one-state and one-stage” framework. a DP network of PATH. b DP network of MSPATH

Full size image

As pointed out by Yoshimoto et al. [66], when the one-stage look-ahead period becomes insufficient to evaluate impacts on the future stand, then MSPATH becomes necessary. Such situations include the following: (1) when there is no thinning at the next stage, implying too much thinning at the previous stage and (2) when intensive thinning is required at the current stage, allowing a great potential growth of the residual stand over the long-term, not the short-term. Intolerant trees show this type of growth over time with the heavy sigmoid-shape of growth curve. If this is the case or there exists influence of thinning control over multiple periods, i.e., multi-stage look-ahead, the DP network changes to the representation in Fig. 2b, with the optimality equation now defined by,

$$ \begin{array}{l}{f}_i^{*}=\underset{\left\{\mathbf{u}\left({t}_{i-j}\right),j\right\}}{ \max}\left\{{f}_{i,i-j}\right({\mathbf{u}}_i\left({t}_{i-j}\right)\Big\}\\ {}{f}_{i,i-j}\left({\mathbf{u}}_i\left({t}_{i-j}\right)\right)={I}_{i,i-j}+{I}_{i,i-j}^u+\left\{{f}_{i-j}^{*}-{I}_{i-j}^{*}\right\}\end{array} $$
(8)

in order to search for an optimal thinning control as well as optimal elapse of time, j, to implement the control. More scripts are introduced to differentiate the thinning control with different elapse of time. Note that I i , i − j  = I(x(t i )| x(t i − j ), u i (t i − j )), u i (t i − j ) is the thinning control implemented at time t i − j targeting the forest stand at time t i , \( {I}_{i,i-j}^u=I\left({\mathbf{u}}_i\left({t}_{i-j}\right)\right) \), j * is an optimal elapse of time (t i  − t i − j ) targeting the state at time t i , \( {I}_{i-j*}^{*}={I}_{i,i-j*}\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_{i-j*}\right),{\mathbf{u}}_i^{*}\left({t}_{i-j*}\right)\right) \), and \( {\mathbf{u}}_i^{*}\left({t}_{i-j*}\right) \) is an optimal thinning control at time t i − j* targeting the forest stand at time t i . This is the case for MSPATH algorithm, which requires more computational time but can overcome the effect of thinning control over multiple periods. Applications of NLP to thinning optimization are categorized in the “multi-stage look-ahead” framework of MSPATH, since the intensity and timing of thinning activities can independently be searched over multiple periods.

The algorithm for PATH and MSPATH is the forward recursive process and works as follows. At each period, i, based on the optimal state vector of a forest stand (if i = 0, it is an initial state vector, x 0), under the forward recursive procedure, the best thinning control is sought by maximizing the sum of the contribution from the thinning control, \( {I}_{i+j,i}^u=I\left({\mathbf{u}}_{i+j}\left({t}_i\right)\right) \), and that from the forest stand toward the target period, I i + j , i  = I(x(t i + j )| x(t i ), u i + j (t i )), and saved the set of the best thinning controls with different time elapse, \( \left\{{\mathbf{u}}_{i+j}^{**}\left({t}_i\right)\right\} \), as well as the corresponding state vector toward each target period with different time elapse, (j = 1, 2,  ⋯ , n − 1). This generates the set of candidates for each target period from the current. Next, after one period growth, the best thinning control as well as time elapse from the past periods is searched and the corresponding best state vector with the best thinning control is selected and used for the future projection for thinning until the end of the planning period.

$$ \left({\mathbf{u}}_i^{*}\left({t}_{i-j*}\right),{j}^{*}\right)=\underset{\left\{{\mathbf{u}}_i^{**}\left({t}_{i-j}\right),j\right\}}{ \arg \max}\left\{I\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_{i-j}\right),{\mathbf{u}}_i^{**}\left({t}_{i-j}\right)\right)+I\left({\mathbf{u}}_i^{**}\left({t}_{i-j}\right)\right)\right\} $$
(9)

At each period, the optimal thinning regime from the initial state is obtained, so that the optimal rotation is derived as the one with the optimal objective value over the planning horizon. If u i (t i − j ) is multivariate, the region-limiting strategies (RLS) can be applied with PATH or MSPATH [15, 34, 65]. As Yoshimoto et al. [36] pointed out, computational efficiency is performed by partitioning the entire problem into partial optimization problems at each period for thinning control such as in the concept of DP.

In order to overcome the multiple period dependency problems due to development of more complicated growth models and ill-behaved financial functions, there is still a case where the thinning control affects the state dynamics over periods, which is overlooked by MSPATH. Such a case was found when we analyzed optimal thinning regime under the thinning subsidy program in Japan. The subsidy is applied at a certain period for a fixed percent of thinning, resulting in conversion of a smooth response surface into the ill-behaved response surface. Too much thinning at an early stage would miss a great opportunity for the subsidy. Whenever we use ill-behaved financial function, there is always the risk of facing heavy dependency of multiple periods. A new approach can be proposed to overcome further dependency, which is two-directional multi-stage PATH (called TMSPATH). In TMSPATH, two types of an optimal time elapse for implementing the thinning control are considered. One is the same as above for the forward recursion, while the other is an elapse of time from the past thinning control for the backward recursion. The backward recursive search is only implemented among the derived candidates by the forward recursive search from the past to the current period. That is, the best combination from the “past” and to the “future” elapse of time is obtained to search for an optimal thinning control at each period. Although the DP network for TMSPATH is the same as that for MSPATH, searching is conducted in two directions (backward and forward) for TMSPATH as opposed to one direction (forward) for MSPATH as well as PATH. The “best” time elapse from the past is selected among those time elapses to the current from the past with the corresponding state and thinning control vector. The optimality equation for TMSPATH becomes:

$$ {f}_i^{*}=\underset{\left\{\mathbf{u}\left({t}_{i-j}\right),j,k\right\}}{ \max}\left\{{f}_{i,i-j}\left({\mathbf{u}}_i\left({t}_{i-j}\right),{\mathbf{u}}_{i-j}^{**}\left({t}_{i-j-k}\right)\right)\right\}{f}_{i,i-j}\left({\mathbf{u}}_i\left({t}_{i-j}\right),{\mathbf{u}}_{i-j}^{**}\left({t}_{i-j-k}\right)\right)={I}_{i,i-j}+{I}_{i,i-j}^u+{I}_{i-j,i-j-k}^{u**}+\left\{{f}_{i-j-k}^{*}-{I}_{i-j-k}^{*}\right\} $$
(10)

The difference between MSPATH and TMSPATH is the third term in the right-hand side of Eq. (10) and an additional time elapse of t i − j − k toward time t i − j . Again, \( \left\{{\mathbf{u}}_{i-j}^{**}\left({t}_{i-j-k}\right)\right\} \) is the candidate best thinning control at time t i − j − k toward a forest stand at time t i − j .

Figure 3 depicts the image of the different recursive processes at time t i − 1 by PATH and t i − j by MSPATH and TMSPATH. The dashed lines for PATH and MSPATH in Fig. 3 are the selected optimal thinning control from the past with one period elapse of time for PATH and multiple period elapse of time for MSPATH and used for future search. On the other hand, the dashed lines for TMSPATH in Fig. 3 are those derived and selected thinning controls \( \left\{{\mathbf{u}}_{i-j}^{**}\left({t}_{i-j-k}\right)\right\} \) from the past different periods toward time t i − j . One solution from each period is chosen. In TMSPATH, based on each solution from the past \( \left\{{\mathbf{u}}_{i-j}^{**}\left({t}_{i-j-k}\right)\right\} \), one thinning control at time t i − j toward a forest stand at time t i is selected among {u i (t i − j )} derived, so that the same number of the candidate solutions are derived as the number of the past periods to time t i − j . Once all solutions from the different past periods are generated, one set of the backward solution from the past \( \left\{\left\{{\mathbf{u}}_{i-j}^{\ast}\left({t}_{i-j-{k}^{\ast }}\right)\right\}\right\} \) and the forward solution \( \left\{{\mathbf{u}}_i^{*}\left({t}_{i-j}\right)\right\} \) to the target period at time t i − j is selected as the optimal thinning controls over two sequential controls toward time t i through time t i − j . This procedure continues from the beginning of the period to the end period.

Fig. 3
figure 3

Comparison of recursive process among PATH, MSPATH, and TMSPATH

Full size image

One of the advantages of DP by the one-state and one-stage framework defined by the above dynamic system over other approaches as well as DP by the “classical” framework is that, the recursive procedure provides useful information on the response surface from the growth simulator used. By changing the degree of the thinning control sequentially at each period, we can have the contribution from the residual forest stand at the target period as well as the contribution from the thinning control at the current period, so that we can investigate how the response surface of the performance index changes with respect to the degree of the control. As long as the surface forms quasi-concave for maximization, the derived solution becomes most likely optimal. If the surface shows ill-behaved phenomena, then we could expect local optima over searching. Figure 4 shows a typical example of the relationship among contribution from thinning control, residual stand, and the response surface. Sequential change on the control is an important process not only for seeking an optimal solution but also for investigating the behavior of the growth simulator. Since the growth simulator is becoming more and more complicated, this kind of task is key for optimization. Note that the DP approach by the classical framework and other approaches do not have this characteristic from the recursive procedures.

Fig. 4
figure 4

Response surface with respect to thinning control

Full size image

When dealing with multiple control variables such as the ones in Yoshimoto et al. [36], Bettinger et al. [15], and Graetz et al. [67], the region-limiting strategies under PATH, MSPATH, or TMSPATH can be applied. NLP approaches can also be used to search for the best multiple control variables; however, again NLP cannot provide information on the response surface but the solution.

Several researchers including Miina [82], Vettenranta and Miina [83], Miina and Pukkala [30], Möykkynen et al. [29], Wikström and Eriksson [84], Wikström [46], Hyytiäinen and Tahvonen [85], and Ribeiro et al. [74] tackled the thinning optimization problems with distance-dependent control variables for the growth simulator. Only Ribeiro et al. [74] applied DP by MSPATH. Distance-dependent growth simulator has the site-specific tree growth dynamics, so that the thinning control is to “cut a tree” or “leave a tree” in a forest stand for future growth. Depending on a tree to be cut, the growth of the residual stand differs. In such a case, we apply two phase RLS for optimization. Let us defined the ordered control vector as follows. Let us set \( {\mathbf{u}}_i^{(k)}\left({t}_{i-j}\right) \) as the control vector of having k trees to be cut. The question is which tree should be included for thinning. RLS can be applied to seek the best one \( {\mathbf{u}}_i^{\left({k}^{\ast}\right)}\left({t}_{i-j}\right) \) among candidates.

$$ {\mathbf{u}}_i^{\left({k}^{\ast}\right)}\left({t}_{i-j}\right)=\underset{{\mathbf{u}}_i^{(k)}\left({t}_{i-j}\right)}{ \arg \kern0.3em \max}\left\{I,\left(\mathbf{x}\left({t}_i\right)|\mathbf{x}\left({t}_{i-j}\right),{\mathbf{u}}_i^{(k)}\left({t}_{i-j}\right)\right),+,I,\left({\mathbf{u}}_i^{(k)}\left({t}_{i-j}\right)\right)\right\} $$
(11)

Once we generate all \( \left\{{\mathbf{u}}_i^{\left({k}^{\ast}\right)},\left({t}_{i-j}\right)\right\} \) with different numbers of trees for thinning, the corresponding response surface can be created to seek the optimal among them as observed in Fig. 5. Empty circles are those inferior to the filled circles with the same number of trees for thinning. By performing this process, we can find the optimal number as well as a set of trees for thinning. PATH, MSPATH, or TMSPATH can be applied to seek the optimal thinning regime for the distance-dependent growth simulator.

Fig. 5
figure 5

Performance frontier for thinning control

Full size image

Conclusions

Forest stand-level planning has a long history of resource managers using optimization techniques to assist them in sorting through alternative management strategies available to them. In this paper, we present an overview of some of the operation research techniques used in forest stand-level planning. We highlight the strengths and weaknesses of these techniques to assist resource managers and operation researchers in their model selection.

The review showed that optimization algorithms often need to be embedded in growth models for iterative calculation, so that development of an optimization model can be conducted jointly with growth modelers and systems analysts. As can be seen from this review, the NLP approach is used more often than the other approaches due to the complexity of the growth model such as distance-dependent and mixed forests. Most growth and yield models are simulators that consist of several sub-models which are difficult to maximize analytically. The derivative-free NLP techniques such as Hooke and Jeeves are suitable for optimizing non-smooth dynamics that are not differentiable.

We also noted that there are many stand-level problems or growth models that are too complex to be solved using most optimization techniques within a reasonable timeframe. These types of problems may be best handled by heuristic techniques. However, the main concern with these techniques is that the final or optimal solution searched generally does not have optimal attributes but is guaranteed to be the best among the generated group of solutions. A reasonable computational time for seeking a feasible and near-optimal solution is the main benefit of using heuristics.

Finally, we put together a strong reason to advocate for the use of DP over other optimization techniques. DP has major advantages that include the ability to find a global optimum. Unlike NLP or heuristic approaches, they do guarantee the finding of a global optimum as long as the DP network for the target problem is “appropriately” constructed. In such a situation, the DP approach is more efficient and permits practical consideration of a larger number of alternatives.

We concluded this review paper by providing the general formulation and solution techniques for forest stand-level planning, including PATH, MSPATH, and a newly proposed TMSPATH algorithm within the one-state and one-stage framework. With the use of the one-state and one-stage framework, the recursive procedure provides useful information on the response surface from the growth simulator used. The form of the response surface plays a key role in judging if the final solution becomes globally optimal or locally optimal. When dealing with multiple control variables as well as distance-dependent growth simulators, the region-limiting strategies under PATH, MSPATH, or TMSPATH can be applied with the ordered control vectors. Note that the DP network by MSPATH can describe most NLP and heuristics searching networks as well, since NLP is seeking the best combination of time elapse and controls over time. Only the process and criterion to choose a solution path is different. Another concern for forest stand-level planning is advanced development of more complex growth simulators in user-friendly applications. Although those growth simulators are easy to use for the end-users, it seems difficult for systems analysts to implement recursive procedure in modeling due to programming language difficulty. In such a case, however, if the growth simulator can provide information for the state vector describing forest stand status at each period as well as control, then the script type of iteration process can be conducted and programmed to seek an optimal solution. That is, we do not need to embed the iterative process into the simulators.