Abstract
We present a technique that examines handwritten equations from a student’s solution to an engineering problem and from this estimates the correctness of the work. More specifically, we demonstrate that lexical properties of the equations correlate with the grade a human grader would assign. We characterize these properties with a set of features that include the number of occurrences of various classes of symbols and binary and tripartite sequences of them. Support vector machine (SVM) regression models trained with these features achieved a correlation of r = .433 (p< .001) on a combined set of six exam problems. Prior work suggests that the number of long pauses in the writing that occur as a student solves a problem correlates with correctness. We found that combining this pause feature with our lexical features produced more accurate predictions than using either type of feature alone. SVM regression models trained using an optimized subset of three lexical features and the pause feature achieved an average correlation with grade across the six problems of r = .503 (p< .001). These techniques are an important step toward creating systems that can automatically assess handwritten coursework.
Similar content being viewed by others
Introduction
The ready availability of large amounts of data from educational software systems has enabled data mining techniques to be used to examine a wide range of education research questions (Romero and Ventura 2010). For example, log files from intelligent tutoring systems (e.g., Stevens et al. 2005) and learning management systems (e.g., Krüger et al. 2010) are common sources of data for mining. However, in many disciplines — particularly science, technology, engineering, and math (STEM) — learning involves a substantial amount of problem solving with paper and pencil, which is more challenging to mine than text-based work.
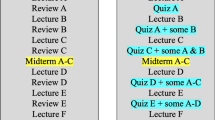
In previous work (Stahovich and Lin 2016), we developed techniques capable of extracting text information from handwritten solutions to engineering problems like the one in Fig. 1b. As an example of the utility of these methods, we used them to examine the relationship between the amount of writing in a student’s handwritten solution to an exam problem and the correctness of the work. More specifically, we found that the total number of alphabetic characters (i.e., the 26 English characters), the number of units of measure (e.g., “kg” and “ft”), and the number of equation groups each correlated positively and significantly with the grade assigned by a human grader. An equation group is a string of characters belonging to a single equation and written on the same baseline (Fig. 2). This work also demonstrated that the number of long pauses between characters correlated positively and significantly with the grade.
Rectangles indicate typical equation groups from Fig. 1b
This prior work primarily examined the relationship between the amount of writing and the correctness of a solution. Here, we examine the hypothesis that the types of content comprising a solution, and the sequences in which it is arranged, relate to the correctness. For example, skilled problem-solvers often solve problems by manipulating the equations in symbolic form, and avoid substituting numerical values into the variables until the final step. One advantage of this approach is that it facilitates the identification of errors. For example, while it is clear that “F = m ∗ v” is an incorrect statement of Newton’s second law (force relates to acceleration not velocity), it is not readily apparent if “F = 20.0 * 4.5” is a correct statement of this law. Likewise, manipulating symbolic variables reduces transcription errors that can occur when manipulating multi-digit real numbers. Thus, having a majority of non-numerical symbols rather than numbers may be indicative of correctness.
In short, the present work examines the hypothesis that lexical properties of a student’s handwritten solution to a problem in a STEM course correlate with the correctness of the solution. We consider a number of lexical properties including the number of occurrences of various classes of symbols (e.g., letters, numbers, and mathematical symbols), the number of occurrences of various binary sequences of characters (e.g., a digit followed by a letter), and the number of tripartite sequences (e.g., a digit followed by a mathematical symbol followed by a letter). Likewise, we also consider the number of equation groups and the number of occurrences of units of measure from (Stahovich and Lin 2016). We refer to these as “lexical properties” to emphasize that we do not consider the semantics of the symbols. Said differently, we do not interpret the meaning of the written solution but rather consider only the quantities of various types of textual elements.
As the work in (Stahovich and Lin 2016) suggests that the number of long inter-character pauses that occur as a student solves a problem in a STEM course is related to the correctness of the solution, we include this feature in our models. Similar to the lexical features, this feature can be computed without interpreting the meaning of the solution.
For our present study, we used Livescribe smartpens to collect a dataset of handwritten solutions to exam problems from an undergraduate engineering course on statics. The smartpens have an integrated camera and are used with dot-patterned paper. They serve the same function as a traditional ink pen and also record the work as time-stamped pen strokes, thus enabling both temporal and spatial analysis of the writing. Statics is the subdiscipline of engineering mechanics that examines the equilibrium of structures subject to forces. The solution to a statics problem typically includes free body diagrams and equilibrium equations. The former represent the forces acting on a system, while the latter are the application of Newton’s Second Law. Figure 1a shows a typical problem from an undergraduate statics course and Fig. 1b shows the sort of solution a student might generate for that problem.
This work demonstrates that the lexical properties of handwritten solutions to a problem in an undergraduate engineering course are predictive of the correctness of the solution. This work could provide the basis for an automated system to provide students with feedback on their homework. In large undergraduate STEM courses, it is often impractical to manually grade students’ homework. Our techniques provide an inexpensive and scalable means of estimating the correctness of this work. By examining the entire solution to a problem, our techniques complement traditional online homework systems that consider only the final answer (Demirci 2010). This sort of automated feedback would also be useful for online courses. While online courses provide an efficient means for delivering course content, there are currently no cost-effective methods for assessing handwritten work. Our techniques could provide the basis for creating such a method.
Related Work
Recent research has begun to examine the relationship between the amount of writing a student produces and academic achievement (Rawson et al. 2017; Van Arsdale and Stahovich 2012). For example, Rawson et al. (2017) examined students’ writing on homework assignments in an introductory engineering course and found that the amount of writing, measured both in terms of the number of pen strokes and the length of ink written, correlated positively and significantly with course grade. Similarly, Van Arsdale and Stahovich (2012) found that the amount of effort on equations correlated positively and significantly with the correctness of the work. These studies examined the amount of writing, not the content, and found that it correlated positively with outcomes. In the present work, we build upon these results by examining how lexical properties of the content correlate with the correctness of a student’s work.
Van Arsdale and Stahovich (2012) examined the relationship between the temporal and spatial organization of a student’s handwritten solution to a statics problem and the correctness of the work. They computed 10 features describing the organization of the solution process and used them to construct stepwise regression models predicting the grade students achieved on the work. Our work is complementary in that we consider lexical properties of equations rather than the organization of the solution process.
Cheng and Rojas-Anaya (2008) examined pauses that occurred as students copied equations and found that the number of long pauses correlated negatively with competence. They defined a long pause as one longer than twice the median pause occurring while the student wrote his or her name. By contrast, Stahovich and Lin (2016) found that the number of long inter-character pauses during problem solving correlated positively with the correctness of the solution. The difference in the sign of the correlations is likely due to the nature of the tasks: one considers a copying task while the other considers a problem-solving task. We employ the pause measure from (Stahovich and Lin 2016) in the present work.
Research in educational data mining has seen a dramatic increase in the past few years (Romero and Ventura 2010). Much of the data used in this work is extracted from log files of intelligent tutoring systems (Stevens et al. 2005; Beal and Cohen 2008; Shanabrook et al. 2010; Mostow et al. 2011; Li et al. 2011; Trivedi et al. 2011) and learning management systems such as Moodle or Blackboard (Krüger et al. 2010; Romero et al. 2010). Our work differs from this in that we record and mine data from learning activities in natural environments, rather than online environments. The work of Oviatt et al. (2006) suggests that natural work environments are critical to student performance. In their examinations of computer interfaces for completing geometry problems, they found that “as the interfaces departed more from familiar work practice…, students would experience greater cognitive load such that performance would deteriorate in speed, attentional focus, meta-cognitive control, correctness of problem solutions, and memory.”
While assessment is a critical element of effective instruction (Pellegrino et al. 2001; Bransford et al. 2000), it can be a burdensome task. Thus, educators have long sought to create methods for automating it. Gikandi et al. (2011) present a recent overview of online assessment tools. Multiple-choice exams are perhaps the most common automated offline tool. While such exams are inexpensive to grade, they generally capture the product of thinking rather than the process. Our techniques are complementary as they consider all of the work for a traditional handwritten problem, not just the final answer.
There have been some efforts to develop tools to facilitate manual grading of handwritten coursework (Schneider 2014; Singh et al. 2017), but there is relatively little work addressing automated grading. Recently, there has been some progress in developing systems for automatically grading handwritten essays (Srihari et al. 2007; Sharma and Jayagopi 2018). These systems first use optical handwriting recognition techniques to identify the text, and then apply automated essay scoring techniques to score the writing. As handwritten solutions to problems in STEM courses are dissimilar from essays, these techniques are not suitable for our task. One fundamental difference is that the text in an essay is written in a highly structured way (e.g., lines of text written from left to right and proceeding down the page), while the writing for a problem solution (e.g., Fig. 1b) is typically scattered around the page in a loosely structured fashion. Additionally, essays employ a known lexicon, whereas the combinations of symbols in a solution to a STEM problem are arbitrary. Researchers have developed techniques for interpreting handwritten equations (Smithies et al. 1999; LaViola and Zeleznik 2004; de Silva et al. 2007; LaViola 2007). These techniques are suitable for interpreting isolated equations and often require the user to draw in a structured manner or to use gestures to guide the interpretation. Thus, these techniques are unsuitable for our task, as the homework solutions we consider contain freeform writing.
Recently, Rawson and Stahovich (2013) and Rawson et al. (2017) examined the relationship between homework effort and course grade. Effort was represented by a set of features describing the amount of writing and the distribution of the writing activity over the assignment period. The features were used to construct regression models predicting course grade. These models demonstrated that the amount of writing correlated positively and significantly with course grade. Herold et al. (2013a) used a related approach that considered both the effort on individual problems and on the assignment as a whole. Herold et al. (2013b) represent homework activity as sequences of actions, including diagram drawing, equation writing, and taking breaks. They used differential data mining techniques to differentiate the activity sequences of students who achieved a high exam grade from those who achieved a low grade. All of these studies examined homework activity (effort) to predict future achievement in the course. By contrast, our work examines the lexical properties of equations written in solutions to exam problems to predict the correctness of the solutions.
Herold and Stahovich (2012) used smartpens as an assessment tool to examine how self-explanation affects the order in which students solve assigned homework problems. The study found that students who generated self-explanations of their work were more likely to finish each problem before starting the next compared to students who did not generate self-explanations.
More traditional educational data mining techniques have also been used to examine learning activities in statics courses. For example, work by Steif and Dollár (2009) examined usage patterns of a web-based statics tutoring system and found that learning gains increased with the number of tutorial elements completed. Similarly, work by Steif et al. (2010) examined whether students can be induced to talk about the bodies in a statics problem, and if doing so can increase a student’s performance. They used tablet PCs to record the students’ spoken explanations and their handwritten solutions, but the written work was left mostly unanalyzed.
Method
We used Livescribe smartpens to capture students’ handwritten solutions to exam problems written on dot-patterned paper. The pens digitize pen strokes as they are written and store them as sequences of time-stamped Cartesian coordinates. We used techniques from Stahovich and Lin (2016) to process the pen stroke data into a form suitable for data mining. In the first step of processing, the equation pen strokes are separated from other content such as diagrams. Then the equation pen strokes are grouped, first into individual equations, and then into individual characters. Finally, after a character recognizer is used to recognize each individual character, a hidden Markov model is used to correct recognition errors.
Once the pen strokes have been recognized, we characterize a problem solution by computing features that characterize lexical properties of the equations. Some features describe the number of occurrences of various symbols and symbol combinations. One feature, for example, describes the number of occurrences of units of measure (e.g., “kg”), while another describes the number of occurrences of a letter following a mathematical operator. We also compute a feature counting the number of long inter-character pauses in the writing. We use support vector machine (SVM) regression models to relate these features to the correctness of the work. We take the grade assigned by a human grader to represent the correctness of a solution.
The next section describes the techniques we use to process the digital pen stroke data. This is followed by a description of our features and the dataset we used in this work.
Recognizing Equation Text
We use techniques from Stahovich and Lin (2016) to process the pen stroke data so that we can extract lexical features from it. Here we provide a brief summary of these techniques. Complete details can be found in (Stahovich and Lin 2016).
Handwritten solutions to engineering problems, like the one in Fig. 1b, contain a variety of content including diagrams, equations, and cross-outs. (Because the digital pens use ink which cannot be erased, students must cross out incorrect work.) The first step of processing is to identify which ink belongs to equations. This is accomplished with two filters. The first uses a set of heuristics to distinguish cross-outs from equations and diagrams. The second uses an AdaBoosted J48 decision tree, trained with a set of features describing the spatial and temporal properties of the pen strokes, to distinguish the equations from the diagrams.
Once the equation pen strokes have been identified, they are grouped into individual equation groups. As shown in Fig. 2, an equation group is a string of characters belonging to a single equation and written on the same baseline. One equation may comprise multiple equation groups. For example, if an equation wraps to a second baseline, there will be two equation groups, one for each baseline. Similarly, if a fraction is written with a horizontal fraction bar (vinculum), the numerator and denominator will likely be identified as separate equation groups.
We focus on equation groups, rather than complete equations, for the sake of simplicity. Identifying complete equations is a difficult problem for which no solutions currently exist. Consider, for example, the three equation groups in the lower right portion of Fig. 2. These three groups form a single equation:
However, identifying this would require complex semantic analysis of the writing. As the focus of our present study is to determine the relationship between lexical properties of a student’s handwritten solution — rather than semantic content — and the correctness, we avoid the complexity of the semantic analysis.
The equation grouper uses a classifier to determine if a pair of pen strokes belongs to the same equation group. The pairwise classifier is a J48 decision tree, implemented in WEKA (Hall et al. 2009) and trained using three features computed from the bounding boxes of the two pen strokes. Figure 3 shows the bounding boxes of two pen strokes and the four distances used to compute the features. The feature GY describes the vertical overlap of the bounding boxes. If yA and yB are the heights of the bounding boxes, and yO is their vertical overlap, then \(G_{Y} = \max (\frac {y_{O}}{y_{A}}, \frac {y_{O}}{y_{B}})\). GY is large if one of the characters lies mostly within the vertical extent of the other. A large value of GY suggests that the two pen strokes lie on the same baseline.
The feature GD is related to the Manhattan distance. If xD is the horizontal distance between the bounding boxes, GD is defined as xD − yO. If the bounding boxes overlap horizontally, xD = 0. GD compares the horizontal spacing between two strokes to the vertical overlap between them. If the former is small compared to the latter, the strokes are near each other horizontally.
The feature GA2 is the ratio of the area of the intersection of the bounding boxes to the area of their union. However, before computing this ratio, the bounding boxes are expanded if they are too small. If the height of a bounding box is less than the median bounding box height, the box is expanded to that height. The width is adjusted analogously. Additionally, the width of each bounding box is then doubled to emphasize the horizontal arrangement of the strokes. The medians are computed separately for each problem solution. A large value of GA2 provides additional evidence that two pen strokes are near each other and are on the same baseline.
To group pen strokes into equation groups, the pairwise classifier is applied to every pair of strokes. A chaining process is then used to merge pairs of grouped strokes that share a common stroke. For example, if the pairwise classifier groups stroke A with B and B with C, the chaining process will combine A, B, and C into one group. Sometimes subscripts are not properly grouped with an equation. As a remedy, small equation groups containing less than five strokes are merged with the nearest equation group if that group is nearby.
Once the pen strokes have been grouped into equations, it is necessary to group the strokes into individual characters so they can be recognized. For example, the letter “X” is typically drawn with two pen strokes. These two strokes must be grouped into a single multi-stroke character before the letter can be recognized.
Characters are grouped using a variation on the equation grouper employing only two features, GA and GX. GA is similar to GA2, but the widths of the bounding boxes are not doubled. GX is similar to GY but considers horizontal overlap of the bounding boxes: \(G_{X} = max(\frac {x_{O}}{x_{A}},\frac {x_{O}}{x_{B}})\). Here xA and xB are the widths of the bounding boxes of the two strokes, and xO is their horizontal overlap. As before, these features are used to train a J48 decision tree. This classifier is applied to all pairs of strokes in an equation group to determine which pairs form multi-stroke characters. Grouped pairs can chain together to form larger characters.
After the individual characters in a solution have been located, an image-based recognizer (Kara and Stahovich 2005) is used to recognize them. The recognizer uses a database of handwritten symbols to identify each character group. An approach based on a hidden Markov model (HMM) is used to correct recognition errors. Some errors are due to variations in writing style. Others result from ambiguity. For example, a lowercase “t” can be confused with a “+” and the number “1” can be confused with the letter “i”. The HMM uses local context to correct errors. For example, imagine that the recognizer identifies a sequence of characters as “s1n”. The HMM will examine the sequence and determine that “sin” is a more likely interpretation than “s1n”.
During error correction, the output of the image-based recognizer is considered to comprise the observations and the true identity of the characters are the hidden states. The Viterbi algorithm (Rabiner 1989) is used to compute the most likely sequence of hidden states to produce the observations. This sequence is then used as the interpretation of the equation.
Extracting Features from Equation Groups
Once the equations have been recognized, we compute 25 features from the text as summarized in Table 1. The first feature, FE is the number of equation groups identified by the equation grouper.
Several features describe the number of occurrences of various classes of symbols. FD is the number of individual digits in the solution (i.e., 0 – 9). FL is the number of letters, including both the English alphabet and the Greek letters ‘𝜃’ and ‘ϕ’, which are often used to represent angles. We include only these two Greek letters (and ‘Σ’) because they occur far more frequently in our dataset than other Greek letters. FM is the number of mathematical symbols including ‘+’, ‘-’, ‘*’, ‘/’, and ‘=’. The number of parentheses is excluded in the count of mathematical symbols. FΣ is the number of occurrences of the symbol ‘Σ’, which is typically used in equation prototypes (see below). Finally, FC is the total number of characters in the solution: FC = FD + FL + FM + FΣ + N(), where N() is the number of parentheses. (While we include the number of parentheses in the total count of characters, we found that excluding this from the count of mathematical symbols resulted in slightly higher prediction accuracy.) Three features describe the relative number of occurrences of the three most common symbol classes: FD/L = FD/FL, FD/M = FD/FM, and FL/M = FL/FM. Finally, FU is the number of units of measure in the solution, including “kg”, “g”, “kN”, “N”, “m”, “lb”, “ft”, and “in”. To be identified as such, units must be immediately preceded by a digit such as “7 lb”.
The next two categories of features are the number of occurrences of binary and tripartite sequences of digits (D), letters (L), and mathematical symbols (M). The features Fij for i, j ∈{D, L, M} are the number of occurrences of binary sequences. For example, FDM is the number of pairs of characters containing a digit followed by a mathematical symbol. The feature F=D considers the number of occurrences of the specific sequence in which an equal sign is followed by a digit, such as “= 4”. Equal signs are important as they are one indication of the number of complete equations. The features FiMj for i, j ∈{D, L} are the number of occurrences of tripartite sequences. For example, FDML is the number of character sequences containing a digit, mathematical symbol, and letter, in that order.
Our set of lexical features is inspired by aspects of effective problem-solving approaches. For example, students in STEM courses are often encouraged to solve problems symbolically and then to plug in the numbers at the end. It is believed that manipulating symbols, rather than numbers, makes the concepts more evident to the student and reduces transcription errors. Likewise, students are encouraged to write units of measure (e.g., “kg” and “ft”) for the various quantities when solving physics-based problems. Problem-solving errors often result in inconsistent or incorrect units. Thus, explicitly writing units can help students to identify errors. Similarly, when solving mechanics problems, students are encouraged to write equation prototypes such as “ΣFX = 0”, which is read as “the sum of the forces in the x-direction equals zero.” Equation prototypes guide students in writing equilibrium equations. By representing the number of occurrences of the various classes of symbols, and the various combinations of them, our features model aspects of a student’s problem-solving approach. Thus, we predict that these features will correlate with the correctness of the work.
The final feature, which is taken from (Stahovich and Lin 2016), characterizes the number of pauses between characters. The feature FP is the number of inter-character pauses longer than the median inter-character pause.
Dataset
We used Livescribe smartpens to collect exam solutions from an undergraduate mechanical engineering course in statics taught at the University of California, Riverside. A total of 147 students enrolled in the course and 138 completed it. The course included two midterm exams and a final exam. Here we use data from the midterm exams. The data comprises a total of 1,069,918 pen strokes, of which 72% are equation strokes.
After we collected the midterm exam data, we manually partition it into individual problem solutions. To do this, we rendered each page of digital ink and interactively separated it by problem. In this way, we created a dataset containing 79 solutions for Midterm 1 Problem 1 (P1), 113 solutions for Midterm 1 Problem 2 (P2), 76 solutions for Midterm 1 Problem 3 (P3), 77 solutions for Midterm 2 Problem 1 (P4), 82 solutions for Midterm 2 Problem 2 (P5), and 48 solutions for Midterm 2 Problem 3 (P6).
The exam problems were graded by teaching assistants based on rubrics developed by the course instructor. These rubrics assigned credit for the correctness of individual problem-solving steps as well as the overall correctness of the solution. To verify the reliability of the grading, we randomly selected exams from 25 students and regraded the problems. As we did not have access to the rubric for problem P2, we did not regrade this problem. Also as not all students completed all exam problems, the random selection of 25 students resulted in only 22 solutions for 5 of the six exam questions. (There were 25 solutions for problem P1.) The new grades were highly consistent with the original ones. For problems P1, P3, P4, P5, and P6, the correlations between the original grades and the new grades were r = .882, r = .896, r = .780, r = .932, and r = .926, respectively. These correlations are significant at p< .001.
Results
Table 2 shows the means and standard deviations for the 24 lexical features, the pause feature, and grade for each of the six exam problems. By some measures, students produced the least amount of equations for problem P2, and the most for problem P4. For example, the average number of equation groups (FE) for problem P2 is 23.7 and for problem P4 it is 32.1. Likewise, the average number of characters written (FC) for problem P2 is 227.8 and for problem P4 it is 329.1. Interestingly, problem P2 had the lowest average grade of 11.2, while problem P4 had the highest average grade of 16.4. (All problems have a maximum possible grade of 20.) The average number of long pauses (FP) ranged from 45.1 for problem P5 to 69.8 for problem P4. Once again, problem P4 had the largest number of long pauses out of all six problems.
To examine our hypothesis that lexical properties of handwritten solutions correlate with the correctness of the work, we computed Pearson correlations between each of the 24 lexical features and grade for all six problems, both separately and combined. The results are listed in the first 24 rows of Table 3. For the six problems combined (column P:All), all of the correlations are positive and significant. In fact, for 22 of the lexical features, p< .001. (Note that all p values are computed with two tails and the number of degrees of freedom equal to the number of data points minus two.)
For four of the individual problems, the correlations with grade are significant for most of the lexical features. More specifically, for problem P1, all lexical features except FΣ, FD/L, FD/M, and FL/M correlate positively and significantly with grade. For problem P2, all except FΣ, FD/L, and FL/M correlate positively and significantly with grade. For problem P3, all except FL/M correlate positively and significantly grade. For problem P6, all except FΣ, FD/M, FL/M, and FLML correlate positively and significantly with grade. FL/M correlates significantly, but the correlation is negative.
For problem P4, only three lexical features correlate significantly with grade: FE correlates negatively and FD/M and FL/M correlate positively. For problem P5 only one lexical feature correlates significantly with grade: FDD correlates positively.
Table 3 also includes Pearson correlations between the number of long pauses (FP) and grade for all six problems, both separately and combined. The results are listed in the last row of Table 3. For the six problems combined, the correlation is positive and significant (r = .461, p< .001). Furthermore, FP correlates positively and significantly with grade for all individual problems except problem P4. The average correlation coefficient across all six individual problems is r = .405.
As a measure of the collective power of the features for predicting grade, we used them to construct SVM regression models. We began by considering a problem-dependent training approach in which the model for each individual problem was trained and tested using data from only that problem. We constructed the models using WEKA’s SVM regression method (SMOreg) with default parameter values (Hall et al. 2009). This method normalizes the data and uses a polynomial kernel with an exponent of 1.0. We trained the models for all problems, both separately and combined, using 10-fold cross-validation. For this training approach, the dataset is split into 10 equal-size, disjoint subsets. During each of the 10 folds, a model is trained using nine of the subsets, and that model is then used to make predictions for the remaining subset. At the completion of this process, there is a predicted grade for each data point. We characterize the performance of the models in terms of the Pearson correlation (r) between the predicted and actual grades, the root-mean-square error (RMSE) of the predictions, and the mean-absolute error (MAE). The results are listed in Table 4. The rows labeled “P:All” are the results for the six problems combined, while the rows labeled “Ave” are the average performance measures for the six individual problems.
The “All” column in the Table 4 lists the correlations achieved using all of the features: the 24 lexical features and the pause feature. For all problems combined, the correlation with grade is .456 (p< .001), the RMSE is 4.10, and the MAE is 3.28. (When interpreting RMSE and MAE, note that grades range from 0.0 to 20.0). Additionally, the models correlate positively and significantly with grade for four of the six individual problems: P1 (r = .404, p< .001), P2 (r = .342, p < .001), P3 (r = .565, p < .001), and P6 (r = .455, p < .001). The average correlation coefficient across all six individual problems is r = .323, the average RMSE is 4.30, and the average MAE is 3.43.
To examine the relative predictive power of the various types of features, we trained SVM regression models using subsets of them. We considered five subsets: (A) FC which comprises the total number of characters, (B) Lexical features which comprise the complete set of 24 lexical feature, (C) Single features which comprise single item counts {FE, FD, FL, FM, FΣ, FC, FD/L, FD/M, FL/M, FU}, (D) Double features which comprise binary pattern counts {FDD, FDM, FDL, FLD, FLM, FLL, FMD, FMM, FML, F=D}, (E) Triple features which comprise tripartite pattern counts {FDMD, FDML, FLMD, FLML}, and (F) FP which comprises the number of long pauses. These results are listed in Table 4. All six subsets produce models that correlate positively and significantly (p< .001) with grade for the six problems combined. For FCr = .435, for the Lexical features r = .433, for the Single features r = .453, for the Double features r = .440, for the Triple features r = .381, and for FPr = .451.
All six feature subsets produce models that correlate positively and significantly with grade for individual problems P1, P2, P3, and P6. Additionally, the models trained with the Single feature subset also correlate positively and significantly with grade for problem P4. For FC, the average correlation with grade across all six problems is r = .345, for the Lexical features it is r = .321, for the Single features it is r = .363, for the Double features it is also r = .363, for the Triple features it is r = .339, and for FP it is r = .357.
Note that the correlations for FC for the six individual problems listed in Table 4 are smaller than the correlations for FC listed in Table 3. The former are correlations between predicted grades and actual grades using a cross-validation approach in which the training and testing data are disjoint so as to reduce over-fitting. By contrast, the latter are direct correlations between FC and grade.
The results in Table 4 characterize the performance of the models for problem-dependent training. Here, to explore the robustness of the models, we evaluate their performance using a problem-independent training approach. More specifically, when testing a model on data from a particular problem, we train the model on data from the other five problems. This training approach corresponds to a usage scenario in which models trained from previous problems are used to estimate grades on a new problem. The performance of these models is described in Table 5.
When using the problem-independent approach, the models trained using all features as well as the Lexical, Single, and Double feature subsets correlate positively and significantly with grade for problems P1, P2, P3, and P5. The models trained using the FC, Triple, and FP feature subsets correlate significantly with grade for all six problems: for problem P4 the correlations are negative and for the other five problems they are positive. For all features, the average correlation with grade across all six problems is r = .305, for FC it is r = .285, for Lexical features it is r = .302, for Single features it is r = .336, for Double features it is r = .325, for Triple features it is r = .240, and for FP it is r = .296. As is expected, the correlations are smaller, and the RMSE and MAE are larger for the problem-independent training than for the problem-dependent training.
Using too many features in a model often results in over-fitting of the data. Here we examine optimal subsets of the features. We exhaustively enumerated and evaluated all possible models employing three lexical features and the pause feature. We trained these models in a problem-dependent fashion using 10-fold cross validation. Table 6 lists the optimal combination of features for each problem and the corresponding correlation coefficient, RMSE, and MAE. Table 7 contains the coefficients for the optimal regression models. Note that the models are computed using normalized feature values. For all six problems, the correlations are positive and significant. The average correlation across all six problems is r = .503, the average RMSE is 3.60, and the average MAE is 2.89. Figure 4 shows plots of residuals vs. predicted grades for the optimal models.
Residual vs. predicted grade for the optimal SVM models trained using three lexical features and the pause feature. (See Table 6)
Discussion and Future Work
Our results support our prediction that the lexical properties of a student’s handwritten solution to a problem in a STEM course correlate with the correctness of the solution. We found that all of the lexical features correlate positively and significantly (p< .001) with grade for the six problems combined. Furthermore, for four of the six individual problems (P1, P2, P3, and P6), nearly all of the lexical features correlate positively and significantly with grade.
SVM regression models trained in a problem-dependent fashion (i.e., with training and testing data comprising disjoint subsets of data from the same problem) demonstrated that the lexical features, in combination, are predictive of the correctness of a handwritten solution (Table 4). For example, models trained with the complete set of lexical features, as well as those trained with four different subsets of the lexical features (the FC, Single, Double, and Triple subsets), all correlate positively and significantly (p< .001) with grade for the six problems combined.
Prior work in (Stahovich and Lin 2016) demonstrated that the number of long pauses in a student’s handwritten solution to a problem in a STEM course correlates with correctness. Our results demonstrate that our lexical features provide information beyond that provided by the pause feature. In fact, combining the lexical and pause features produced the best performance. For example, the models in Table 6, which each include three lexical features and the pause feature, performed better than the models in Table 4, which comprised only subsets of the lexical features or only the pause feature.
Because of their nature, the various lexical features are correlated with each other. For example, as the total number of characters increases, the number of digits, letters, and mathematical symbols each typically increase as well. Indeed, SVM regression models trained in a problem-dependent fashion using only the number of characters (FC) did correlate positively and significantly with grade for four of the six individual problems (P1, P2, P3, and P6) and for all problems combined. However, the other features do provide additional information as is evident from the optimal models in Table 6. The feature FC was not selected in any of the optimal feature models. Thus, beyond the number of characters, the number of occurrences of the various classes of symbols and binary and tripartite sequences of them are important features for assessing the correctness of a problem.
The correlations for problem-independent training (Table 5) are somewhat smaller than the correlations for problem-dependent training (Table 4). Nevertheless, the fact that problem-independent training produces significant correlations suggests that the methods may be useful in scenarios in which models are trained on existing problems are then used to estimate grades on new problems. However, there are clearly limits to the generality of the models, and exploring this is left to future work.
For both problem-dependent and problem-independent training, models trained using the full set of lexical features failed to produce significant correlations for problem P4. (However, the optimal model did produce a significant correlation with grade.) We suspect that this may be related to the nature of this particular exam question. This problem had the highest average grade out of the six problems. On average, students received 16.4 out of a possible 20 points. We suspect that the weak correlations for this problem are a result of a large number of students performing particularly well so that the distribution of grades was highly skewed. In total, 32% of students received a perfect grade of 20.
For problem P5, problem-dependent training using the full set of lexical features failed to produce a significant correlation. However, problem-independent training with the full set of lexical features did produce a significant correlation, as did the optimal model. This may suggest a problem with over-fitting.
Figure 4 shows plots of the residuals vs. predicted grades for the optimal models from Table 6. For the most part, the residuals are unbiased. The residuals for problem P2 are somewhat heteroscedastic, but this may be a result of the dearth of examples with high grades. The diagonal band in the upper right of the residual plot for problem P4 is a result of the high proportion of students who received perfect grades. Each of these points represents a student who received a perfect grade, and thus the predicted values and residuals are linearly related. This same band appears in the plot for all problems combined.
We believe that our features are predictive of correctness because they characterize aspects of effective problem solving. For example, by characterizing the relative frequency of non-numerical symbols vs. numbers, our features may detect when a student works symbolically and delays the use of numbers until the last step, which is an effective approach to problem solving. Nevertheless, we avoid attempting to interpret the coefficients of the SVM regression models in Table 7 as their meaning is not clear.
Instead, our models are best evaluated in terms of their accuracy at making predictions. Our regression results characterize prediction accuracy as the training and testing data for the models was distinct: the results in Table 4 describe the prediction performance for problem-dependent training using cross-validation, while the results in Table 5 describe performance for problem-independent training in which the training and testing data are form different problems. Said differently, our results characterize performance at extrapolation rather than interpolation.
The best prediction accuracy was achieved by the optimal models described in Table 6, which were also trained in a problem-dependent fashion using cross-validation. For the six individual problems, the models achieved an average correlation coefficient r = .503, an average RMSE of 3.60 and an average MAE of 2.89. On average, these models explained 25% of the variance in the grades (r2 = .253) and, thus are capable of making useful predictions of grades. However, as the RMSE is 3.60 on a grading scale of zero to 20, the predictions are not yet sufficiently accurate for automated grading. The models are best used for providing automated feedback to students. For example, in cases where it is impractical to grade student homework (which unfortunately occurs all too often in large STEM courses), the models could be used to identify students who have poor predicted grades on multiple problems. Those students could then be given additional support with the material. For this application, erroneously low predicted grades would cause no harm.
While an average correlation coefficient of r = .503 is still insufficient for automated grading, these results are none the less surprising. The models do not attempt to interpret a student’s equations or the final answer. In fact, the models do not even consider if a final answer exists. The predictions are based solely on lexical characteristics of the writing and the number of long pauses. We believe that there may be other lexical properties of handwritten equations, not considered by our feature set, that also correlate with correctness. Identifying these could improve prediction accuracy, but that is future work. Likewise, our work is complementary to that of Van Arsdale and Stahovich (2012) who used features characterizing the temporal and spatial organization of a student’s handwritten solution to predict correctness. We expect that combining our features with theirs will produce even more accurate predictions.
It is useful to contrast our task with another automated grading task: automated essay scoring (AES). AES techniques are quite mature. For example, Attali (2015) reported correlations between machine generated scores and human generated scores as high as r = .79. However, this task is considerably different from ours. AES systems work with machine interpretable text, while we work from handwritten pen strokes. Recently, Sharma and Jayagopi (2018) developed a method for automated grading of handwritten essays. They formulated the problem as the task of classifying an essay with one of five possible integer scores in the range from zero to four. Their methods achieved an accuracy of only 38.1% at assigning the correct score, i.e., the score assigned by a human grader. However, as described in Section “Related Work”, even this task is considerably different from ours. For example, essays have a strong spatial organization and a known lexicon, while the handwritten problem solutions we consider do not. Thus, given the complexities of our problem domain, a correlation of r = .503 between predicted and actual grades represents a reasonable level of performance.
Evaluating the validity and reliability of automated grading methods is a complicated matter. For example, Attali (2013) presents an analysis of the validity and reliability of AES methods. He notes that because these methods cannot evaluate the same aspects of writing that human graders do, many researchers evaluate the validity of AES methods simply in terms of their ability to match human-generated scores, without concern for which aspects of the writing the methods actually evaluate. We employ the same approach here. Understanding which aspects of problem solving our methods measure is an interesting and challenging question which is beyond the scope of our present work.
Similarly, we have not yet examined the reliability of our methods. We use the methods in (Stahovich and Lin 2016) to locate and recognize characters and locate equations groups. If these methods cannot interpret the writing, this will affect the computation of the lexical and pause features, and thus could affect the predicted grade. As result, two solutions that differ only in the legibility of the writing may be assigned different grades. Examining this issue is left to future work. Nevertheless, we believe that improving the accuracy of the underlying recognition methods we use will increase our accuracy at predicting grade.
We found that subsets of the features produced the strongest predictions of grade. We performed limited feature subset selection by enumerating all models containing three lexical features and the pause feature and selecting the best-performing ones. In future work, it will be necessary to employ more sophisticated subset selection techniques such as those in (Kohavi and John 1997).
Some of the lexical features are domain-independent, while others like the number of “Σ” characters may be specific to particular STEM subjects. Thus, future research is needed to determine if these results generalize to other STEM courses. Furthermore, replication of these results with other cohorts of students will strengthen the conclusions of this study.
Conclusion
This study demonstrated that the lexical properties of a student’s handwritten solution to an exam problem in an engineering course correlate with the correctness of the work. We developed a set of 24 quantitative features characterizing the lexical properties of handwritten equations. These features include the number of occurrences of various classes of symbols, binary sequences of symbols, and tripartite sequences of symbols. We used these features to construct SVM regression models to predict the correctness of the work, i.e., the grade a human grader would assign.
We evaluated this approach on a dataset containing solutions to six exam problems from an undergraduate engineering course in statics. Students completed the exam problems using digital pens that recorded the work as time-stamped pen strokes. SVM regression models trained using the complete set of lexical features achieved a correlation of r = .433 (p< .001) on the six problems combined, and an average correlation of r = .321 for the problems considered individually.
We also examined the performance of our lexical features in combination with a pause feature that represents the number of long pauses in a student’s handwritten solution (Stahovich and Lin 2016). We found that the two types of features provide complementary information about correctness and that combining the two produced the best performance. For example, SVM regression models trained using an optimized subset of three lexical features and the number of long pauses achieved an average correlation with grade across all six problems of r = .503. This is a surprising result given that our approach does not attempt to interpret the equations or even the final numerical answer. Additionally, unlike more traditional automated grading methods, such as automated exam scoring, our methods work from handwritten pen strokes rather than machine interpretable text.
One important property of our techniques is that they do not require complete semantic interpretation of equations, nor do they require knowledge of the subject matter. Consequently, our techniques should be readily extensible to other subject areas. In particular, we expect that our techniques will be useful for assessing student learning in a variety of STEM subjects.
Our techniques are an important step toward creating systems that can automatically grade handwritten coursework. While our current models cannot yet replace a human grader, our techniques are attractive because of their generality and low cost. By examining the steps used to solve a problem, our techniques complement traditional online homework systems that consider only the final answer.
Change history
13 January 2020
In this issue, the citation information on the opening page of each article HTML was updated to read ���International Journal of Artificial Intelligence in Education December 2019���,��� not ���International Journal of Artificial Intelligence in Education December 2000...���
References
Attali, Y. (2013). Validity and reliability of automated essay scoring. Handbook of automated essay evaluation: current applications and new direction, 181–198.
Attali, Y. (2015). Reliability-based feature weighting for automated essay scoring. Appl. Psychol. Meas., 39(4), 303–313.
Beal, C.R., & Cohen, P.R. (2008). Temporal data mining for educational applications. In Proceedings of the 10th Pacific rim international conference on artificial intelligence: trends in artificial intelligence (pp. 66–77). Berlin: Springer.
Bransford, J.D., Brown, A.L., Cocking, R.R. (Eds.). (2000). How people learn: brain, mind, experience, and school: expanded edition. Washington: The National Academies Press.
Cheng, P.C., & Rojas-Anaya, H. (2008). Measuring mathematic formula writing competence: an application of graphical protocol analysis. In Proceedings of the 13th annual conference of the cognitive science society (pp. 869–874).
Demirci, N. (2010). Web-based vs. paper-based homework to evaluate students’ performance in introductory physics courses and students’ perceptions: two years experience. Int. J. E-Learning, 9(1), 27–49.
Gikandi, J., Morrow, D., Davis, N. (2011). Online formative assessment in higher education: a review of the literature. Comput. Educ., 57(4), 2333–2351.
Hall, M., Frank, E., Holmes, G., Pfahringer, B., Reutemann, P., Witten, I.H. (2009). The WEKA data mining software: an update. ACM SIGKDD Explorations Newsletter, 11(1), 10–18.
Herold, J., & Stahovich, T. (2012). Characterizing students’ handwritten self-explanations. In Proceedings of the 2012 American society for engineering education annual conference and exposition.
Herold, J., Stahovich, T.F., Rawsonm, K. (2013a). Using educational data mining to identify correlations between homework effort and performance. In Proceedings of the 2013 American society for engineering education annual conference and exposition.
Herold, J., Zundel, A., Stahovich, T.F. (2013b). Mining meaningful patterns from students’ handwritten coursework. In Proceedings of the sixth international conference on educational data mining.
Kara, L.B., & Stahovich, T.F. (2005). An image-based, trainable symbol recognizer for hand-drawn sketches. Comput. Graph., 29, 501–517.
Kohavi, R., & John, G.H. (1997). Wrappers for feature subset selection. Artif. Intell., 97(1), 273–324. https://doi.org/10.1016/S0004-3702(97)00043-X, http://www.sciencedirect.com/science/article/pii/S000437029700043X, relevance.
Krüger, A., Merceron, A., Wolf, B. (2010). A data model to ease analysis and mining of educational data. In Proceedings of the 3rd international conference on educational data mining.
LaViola, J.J. Jr. (2007). An initial evaluation of mathpad2: a tool for creating dynamic mathematical illustrations. Comput. Graph., 31(4), 540–553. https://doi.org/10.1016/j.cag.2007.04.008, https://doi.org/10.1016/j.cag.2007.04.008.
LaViola, J.J. Jr, & Zeleznik, R.C. (2004). Mathpad2: a system for the creation and exploration of mathematical sketches. ACM Trans. Graph., 23 (3), 432–440. https://doi.org/10.1145/1015706.1015741, http://doi.acm.org/10.1145/1015706.1015741.
Li, N., Cohen, W.W., Koedinger, K.R., Matsuda, N. (2011). A machine learning approach for automatic student model discovery. In Proceedings of the 4th international conference on educational data mining (pp. 31–40).
Mostow, J., Gonzàlez-Brenes, J.P., Tan, B.H. (2011). Learning classifiers from a relational database of tutor logs. In Proceedings of the 4th international conference on educational data mining (pp. 149–158).
Oviatt, S., Arthur, A., Cohen, J. (2006). Quiet interfaces that help students think. In UIST ’06: Proceedings of the 19th annual ACM symposium on User interface software and technology, ACM Press, New York (pp. 191–200).
Pellegrino, J.W., Chudowsky, N., Glaser, R. (Eds.). (2001). Knowing what students know: the science and design of educational assessment. Washington: The National Academies Press.
Rabiner, L. (1989). A tutorial on hidden markov models and selected applications in speech recognition. Proc. IEEE, 77(2), 257–286.
Rawson, K., & Stahovich, T.F. (2013). Predicting course performance from homework habits. In Proceedings of the 2013 American society for engineering education annual conference and exposition.
Rawson, K., Stahovich, T.F., Mayer, R.E. (2017). Homework and achievement: using smartpen technology to find the connection. J. Educ. Psychol., 109(2), 208.
Romero, C., & Ventura, S. (2010). Educational data mining: a review of the state of the art. Systems, Man, and Cybernetics, Part C: Applications and Reviews, IEEE Transactions on, 40(6), 601–618.
Romero, C., Romero, J., Luna, J., Ventura, S. (2010). Mining rare association rules from e-learning data. Educ. Data Mining, 171–180.
Schneider, S.C. (2014). Paperless grading of handwritten homework: electronic process and assessment. In Proceedings of the American society for enginering education annual conference.
Shanabrook, D.H., Cooper, D.G., Woolf, B.P., Arroyo, I. (2010). Identifying high-level student behavior using sequence-based motif discovery. In de Baker, R.S.J., Merceron, A., Jr, P.I.P. (Eds.) Proceedings of the 3rd international conference on educational data mining (pp. 191–200).
Sharma, A., & Jayagopi, D.B. (2018). Automated grading of handwritten essays. In 2018 16Th international conference on frontiers in handwriting recognition (ICFHR), IEEE (pp. 279–284).
de Silva, R., Bischel, D.T., Lee, W., Peterson, E.J., Calfee, R.C., Stahovich, T.F. (2007). Kirchhoff’s pen: a pen-based circuit analysis tutor. In Proceedings of the 4th eurographics workshop on sketch-based interfaces and modeling, ACM, New York, NY, USA, SBIM ’07 (pp. 75–82).
Singh, A., Karayev, S., Gutowski, K., Abbeel, P. (2017). Gradescope: a fast, flexible, and fair system for scalable assessment of handwritten work. In Proceedings of fourth ACM conference on learning@ scale (pp. 81–88): ACM.
Smithies, S., Novins, K., Arvo, J. (1999). A handwriting-based equation editor. In Proceedings of the 1999 conference on graphics interface ’99, Morgan Kaufmann Publishers Inc., San Francisco, CA, USA (pp. 84–91). http://dl.acm.org/citation.cfm?id=351631.351660.
Srihari, S.N., Srihari, R.K., Babu, P., Srinivasan, H. (2007). On the automatic scoring of handwritten essays. In Proceeddings of international joint conference on artificial intelligence (pp. 2880–2884).
Stahovich, T.F., & Lin, H. (2016). Enabling data mining of handwritten coursework. Comput. Graph., 57, 31–45. https://doi.org/10.1016/j.cag.2016.01.002, http://www.sciencedirect.com/science/article/pii/S0097849316300012.
Steif, P.S., & Dollár, A. (2009). Study of usage patterns and learning gains in a web-based interactive static course. J. Eng. Educ., 98(4), 321–333.
Steif, P.S., Lobue, J.M., Kara, L.B., Fay, A.L. (2010). Improving problem solving performance by inducing talk about salient problem features. J. Eng. Educ., 99(2), 135–142.
Stevens, R., Johnson, D.F., Soller, A. (2005). Probabilities and predictions: modeling the development of scientific problem-solving skills. Cell Biol. Educ., 4(1), 42–57.
Trivedi, S., Pardos, Z.A., Sàrközy, G.N., Heffernan, N.T. (2011). Spectral clustering in educational data mining. In Proceedings of the 4th international conference on educational data mining (pp. 129–138).
Van Arsdale, T., & Stahovich, T. (2012). Does neatness count? What the organization of student work says about understanding. In Proceedings of the 2012 American society for engineering education annual conference and exposition.
Acknowledgements
This material is based upon work supported by the National Science Foundation under Award Numbers 0935239, 1432820, and 1612511. Livescribe, Inc. provided some materials used in the project. We thank Daniel Jeske for his suggestions about some of the statistical analysis.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Stahovich, T.F., Lin, H. & Gyllen, J. Using Lexical Properties of Handwritten Equations to Estimate the Correctness of Students’ Solutions to Engineering Problems. Int J Artif Intell Educ 29, 459–483 (2019). https://doi.org/10.1007/s40593-019-00181-3
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40593-019-00181-3