Skip to main content
SpringerLink
Log in

Period-doubling route to chaos, bistability and antimononicity in a jerk circuit with quintic nonlinearity

  • Published:
International Journal of Dynamics and Control Aims and scope Submit manuscript

Abstract

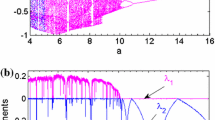
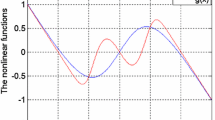
In this paper, the dynamics of an autonomous jerk circuit with quintic nonlinearity is investigated. The circuit is described by a set of three coupled-first order nonlinear differential equations recently introduced as memory oscillator by Sprott (Elegant chaos, algebraically simple chaotic flows, World Scientific, Singapore, 2010). The dynamical behaviors of the system are examined with the help of common nonlinear methods such as bifurcation diagrams, largest Lyapunov exponent plot, Poincaré map as well as power density spectra. It is revealed that the system under scrutiny experiences some complex phenomena including period-doubling route to chaos, bistability and antimonotonicity. Finally, the analog simulations are carried out in PSIM and experimental electronic circuit is realized to validate the numerical results.

This is a preview of subscription content, log in via an institution to check access.

Access this article

Log in via an institution

Price excludes VAT (USA)
Tax calculation will be finalised during checkout.

Instant access to the full article PDF.

Institutional subscriptions

Fig. 1
Fig. 2
Fig. 3
Fig. 4
Fig. 5
Fig. 6
Fig. 7
Fig. 8
Fig. 9
Fig. 10
Fig. 11
Fig. 12
Fig. 13

Similar content being viewed by others

References

  1. Goswami BK, Pisarchik AN (2008) Controlling multistability by small periodic perturbation. Int J Bifurc Chaos 18:1645–1673

    Article  MathSciNet  Google Scholar 

  2. Lynch S (2001) Multistability, bistability and chaos control. Nonlinear Anal Theory Methods Appl 47:4501–4512

    Article  MathSciNet  MATH  Google Scholar 

  3. Upadhyay RK (2003) Multiple attractors and crisis route to chaos in a model food-chain. Chaos Solitons Fractals 16:737–747

    Article  MathSciNet  MATH  Google Scholar 

  4. Pivka L, Wu WC, Huang A (1994) Chua’s oscillator: a compendium of chaotic phenomena. J Frankl Inst 331:705–741

    Article  MathSciNet  MATH  Google Scholar 

  5. Kuznetsov AP, Kuznetsov SP, Mosekilde E, Stankevich NV (2015) Co-existing hidden attractors in a radio-physical oscillator system. J Phys A Math Theor 48:125101

    Article  MathSciNet  MATH  Google Scholar 

  6. Lee EK, Pang HS, Park JD, Lee H (1993) Bistability and chaos in an injection-locked semiconductor laser. Phys Rev A 47:736–739

    Article  Google Scholar 

  7. Ávarez LF, Pla O, Chubykalo O (2000) Quasiperiodicity, bistability, and chaos in the Landau–Lifshitz equation. Phys Rev B 61:11613–11617

    Article  Google Scholar 

  8. Munmuangsaen B, Srisuchinwong B, Sprott JC (2011) Generalization of the simplest autonomous chaotic system. Phys Lett A 375:1445–1450

    Article  MATH  Google Scholar 

  9. Sprott JC (1997) Some simple chaotic jerk functions. Am J Phys 65:537

    Article  Google Scholar 

  10. Sprott JC (2000) Simple chaotic systems and circuits. Am J Phys 68:758–764

    Article  Google Scholar 

  11. Eichhorn R, Linz SJ, Hanggi P (2002) Simple polynomial classes of chaotic jerky dynamics. Chaos Solitons Fractals 13:1–15

    Article  MathSciNet  MATH  Google Scholar 

  12. Schot SH (1978) Jerk: the time rate of change of acceleration. Am J Phys 46:1090

    Article  Google Scholar 

  13. Sprott JC (2010) Elegant chaos, algebraically simple chaotic flows. World Scientific, Singapore

    Book  MATH  Google Scholar 

  14. Sprott JC (2011) A new chaotic jerk circuit. IEEE Trans Circuits Syst II Express Briefs 58:240–243

    Article  Google Scholar 

  15. Kengne J, Njitacke ZT, Nguomkam Negou A, Fouodji Tsostop M, Fotsin HB (2016) Coexistence of multiple attractors and crisis route to chaos in a novel chaotic jerk circuit. Int J Bifurc Chaos 26:1650081

    Article  MATH  Google Scholar 

  16. Kengne J, Njitacke ZT, Fotsin HB (2016) Dynamical analysis of a simple autonomous jerk system with multiple attractors. Nonlinear Dyn 83:751–765

    Article  MathSciNet  Google Scholar 

  17. Kengne J, Negou Nguomkam A, Njitacke ZT (2017) Antimonotonicity, chaos and multiple attractors in a novel autonomous jerk circuit. Int J Bifurc Chaos 27:1750100

    Article  MathSciNet  MATH  Google Scholar 

  18. Vaidyanathan S, Volos C, Pham VT, Madhavan K, Idowu BA (2014) Adaptive backstepping control, synchronization and circuit simulation of a 3-D novel jerk chaotic system with two hyperbolic sinusoidal nonlinearities. Arch Control Sci 24:375–403

    Article  MathSciNet  MATH  Google Scholar 

  19. Vaidyanathan S, Volos C, Pham VT, Madhavan K (2015) Analysis, adaptive control and synchronization of a novel 4-D hyperchaotic hyperjerk system and its SPICE implementation. Arch Control Sci 25:109–135

    Article  MathSciNet  Google Scholar 

  20. Kyprianidis IM, Volos C, Stouboulos IN, Angelopoulos A, Fildisis T (2010) AIP conference proceedings: chaotic dynamics from a nonlinear circuit based on memristor with cubic nonlinearity. In: Hellenic Physical Society (ed) Chaotic dynamics from a nonlinear circuit based on memristor with cubic nonlinearity, AIP Conference Proceedings, pp 626–631

  21. Thamilmaran K, Lakshmanan M, Venkatesan A (2004) Hyperchaos in a modified canonical Chua’s circuit. Int J Bifurc Chaos 14(01):221–243

    Article  MATH  Google Scholar 

  22. Yuan F, Wang G, Shen Y, Wang X (2016) Coexisting attractors in a memcapacitor-based chaotic oscillator. Nonlinear Dyn 86:37–50

    Article  MathSciNet  Google Scholar 

  23. Kamdoum Tamba V, Fotsin HB, Kengne J, Megam Ngouonkadi EB, Talla PK (2017) Emergence of complex dynamical behaviors in improved colpitts oscillators: antimonotonicity, coexisting attractors, and metastable chaos. Int J Dyn Control 5(3):395–406

    Article  MathSciNet  Google Scholar 

  24. Kengne J, Signing VR, Folifack, Chedjou JC, Leutcho GD (2017) Nonlinear behavior of a novel chaotic jerk system: antimonotonicity, crises, and multiple coexisting attractors. Int J Dyn Control. https://doi.org/10.1007/s40435-017-0318-6

  25. Gottlieb HPW (1996) Question 38. What is the simplest jerk function that gives chaos? Am J Phys 64:525

    Article  Google Scholar 

  26. Strogatz HS (2014) Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering. Westview Press, Boulder

    MATH  Google Scholar 

  27. Kuznetsov Y (2004) Elements of applied bifurcation theory, 3rd edn. Applied Mathematical Sciences, New York

    Book  MATH  Google Scholar 

  28. Argyris J, Faust G, Haase M (1994) An exploration of chaos: an introduction for natural scientists and engineers. North-Holland, Amsterdam

    MATH  Google Scholar 

  29. Nayfeh AH, Balakumar B (1996) Applied nonlinear dynamics: analytical, computational, and experimental methods. Bull Math Biol 58:603–606

    Article  Google Scholar 

  30. Hilborn RC (1994) Chaos and nonlinear dynamics: an introduction for scientists and engineers, 2nd edn. American Institute of Physics, College Park

    MATH  Google Scholar 

  31. Press WH, Teukolsky SA, Vetterling WT, Flannery BP (1993) Numerical recipes in Fortran (the art of scientific computing), 2nd edn. Elsevier, North Holland

    MATH  Google Scholar 

  32. Wolf A, Swift JB, Swinney HL, Vastano JA (1985) Determining lyapunov exponents from a time series. Physica D 16:285–317

    Article  MathSciNet  MATH  Google Scholar 

  33. Kaplan JL, Mallet-Paret J, Yorke JA (1984) The lyapunov dimension of a nowhere differentiable attracting torus. Ergod Theory Dyn Syst 4(2):261–281

    Article  MathSciNet  MATH  Google Scholar 

  34. Sprott JC (2003) Chaos and time-series analysis. Oxford University Press, Oxford

    MATH  Google Scholar 

  35. Masoller C (1994) Coexistence of attractors in a laser diode with optical feedback from a large external cavity. Phys Rev A 50:2569–2578

    Article  Google Scholar 

  36. Li C, Sprott JC (2014) Multistability in the lorenz system: a broken butterfly. Int J Bifurc Chaos 24:1450131

    Article  MathSciNet  MATH  Google Scholar 

  37. Pisarchik AN (2001) Controlling the multistability of nonlinear systems with coexisting attractors. Phys Rev E 64:046203

    Article  Google Scholar 

  38. Dawson SP, Grebogi C, Yorke JA, Kan I, Koçak H (1992) Antimonotonicity: inevitable reversals of period-doubling cascades. Phys Lett A 162:249–254

    Article  MathSciNet  Google Scholar 

  39. Pisarchik AN, Goswami BK (2000) Annihilation of one of the coexisting attractors in a bistable system. Phys Rev Lett 84:1423–1426

    Article  Google Scholar 

  40. Ogawa T (1988) Quasiperiodic instability and chaos in the bad-cavity laser with modulated inversion: numerical analysis of a toda oscillator system. Phys Rev A 37:4286–4302

    Article  MathSciNet  Google Scholar 

  41. Parlitz U, Lauterborn W (1985) Superstructure in the bifurcation set of the duffing equation. Phys Lett A 107:351–355

    Article  MathSciNet  Google Scholar 

  42. Parlitz U, Lauterborn W (1987) Period-doubling cascades and devil’s staircases of the driven van der Pol oscillator. Phys Rev A 36:1428–1434

    Article  Google Scholar 

  43. Kocarev L, Halle KS, Eckert K, Chua LO (1993) Experimental observation of antimonotonicity in Chua’s circuit. Int J Bifurc Chaos 03:1051–1055

    Article  MATH  Google Scholar 

  44. Kyprianidis IM, Stouboulos IN, Haralabidis P, Bountis T (2000) Antimonotonicity and chaotic dynamics in a fourth-order autonomous nonlinear electric circuit. Int J Bifurc Chaos 10(08):1903–1915

    Article  Google Scholar 

  45. Dawson SP, Grebogi C, Koçak H (1993) Geometric mechanism for antimonotonicity in scalar maps with two critical points. Phys Rev E 48:1676–1682

    Article  MathSciNet  Google Scholar 

  46. Grassberger P, Procaccia I (1983) Measuring the strangeness of strange attractors. Physica D 9:189–208

    Article  MathSciNet  MATH  Google Scholar 

  47. Kingni ST, Keuninckx L, Woafo P, Van der Sande G, Danckaert J (2013) Dissipative chaos, shilnikov chaos and bursting oscillations in a three-dimensional autonomous system: theory and electronic implementation. Nonlinear Dyn 73(1–2):1111–1123

    Article  MathSciNet  MATH  Google Scholar 

  48. Kingni ST, Jafari S, Simo H, Woafo P (2014) Three-dimensional chaotic autonomous system with only one stable equilibrium: analysis, circuit design, parameter estimation, control, synchronization and its fractional-order form. Eur Phys J Plus 129(5):76

    Article  Google Scholar 

  49. Hamill DC (1993) Learning about chaotic circuits with SPICE. IEEE Trans Educ 36:28–35

    Article  Google Scholar 

  50. Bianchi G, Kuznetsov NV, Leonov GA, Seledzhi SM, Yuldashev MV, Yuldashev RV (2016) Hidden oscillations in SPICE simulation of two-phase costas loop with non-linear VCO. IFAC-Pap Online 49:45–50

    Article  Google Scholar 

  51. Sampath S, Aidyanathan S, Volos C, Pham VT (2015) An eight term novel four-scroll chaotic system with cubic nonlinearity and its circuit simulation. J Eng Sci Technol Rev 8:1–6

    Article  Google Scholar 

  52. Bao BC, Bao H, Wang N, Chen M, Xu Q (2017) Hidden extreme multistability in memristive hyperchaotic system. Chaos Solitons Fractals 94:102–111

    Article  MathSciNet  MATH  Google Scholar 

  53. Kamiriski B, Wejrzanowski K, Koczara W (2004) IEEE35th annual power electronics specialists conference—an application of PSIM simulation software for rapid prototyping of DSP based power electronics control systems. In: An application of PSIM simulation software for rapid prototyping of DSP based power electronics control systems. IEEE, pp 336–341

  54. Kiers K, Schmidt D, Sprott JC (2004) Precision measurements of a simple chaotic circuit. Am J Phys 72(4):503–509

    Article  Google Scholar 

  55. Luchinsky D, McClintock PV, Dykman M (1998) Analogue studies of nonlinear systems. Rep Prog Phys 61(8):889

    Article  Google Scholar 

  56. Jafari S, Li C (2017) Asymmetric bistability in the rossler system. Acta Phys Pol B 48:97–107

    Article  Google Scholar 

  57. Daltzis P, Vaidyanathan S, Pham V, Volos C, Nistazakis E, Tombras G (2017) Hyperchaotic attractor in a novel hyperjerk system with two nonlinearities. Circuits Syst Signal Process 37:1–23

    MathSciNet  Google Scholar 

  58. Venkatasubramanian V, Weijun J (1999) Coexistence of four different attractors in a fundamental power system model. IEEE Trans Circuits Syst I Fundam Theory Appl 46:405–409

    Article  Google Scholar 

  59. Li C, Hu W, Sprott JC, Wang X (2015) Multistability in symmetric chaotic systems. Eur Phys J Spec Top 224:1493–1506

    Article  Google Scholar 

Download references

Acknowledgements

The authors would like to thank Prof. Woafo Paul of University of Yaoundé 1-Cameroon, for suggesting many helpful pieces of advice during the investigation of the work and Dr. Sifeu Takougang Kingni of University of Maroua-Cameroon, for carefully reading the manuscript.

Author information

Authors and Affiliations

  1. Research Unit of Laboratory of Automation and Applied Computer (LAIA), Electrical Engineering Department of IUT-FV, University of Dschang, P.O. Box 134, Bandjoun, Cameroon

    Justin Roger Mboupda Pone & Guillaume Honore Kom

  2. Laboratory of Energetic and Automation (LEA), Automation and Control Laboratory Team (ACL), Electrical Engineering Department of National Advanced School of Engineering, ENSP, University of Yaoundé I, P.O. Box 8390, Yaoundé, Cameroon

    Justin Roger Mboupda Pone

  3. Research Unit of Laboratory of Condensed Matter, Electronics and Signal Processing (LAMACETS) Department of Physics, Faculty of Sciences, University of Dschang, P.O. Box 67, Dschang, Cameroon

    Victor Kamdoum Tamba

  4. Laboratory of Electronics and Signal Processing (LETS), GRETMAT Team, Electrical Engineering Department of National Advanced School of Engineering, ENSP, University of Yaoundé I, P.O. Box 8390, Yaoundé, Cameroon

    Guillaume Honore Kom & Alain Bertin Tiedeu

Authors
  1. Justin Roger Mboupda Pone
    View author publications

    You can also search for this author in PubMed Google Scholar

  2. Victor Kamdoum Tamba
    View author publications

    You can also search for this author in PubMed Google Scholar

  3. Guillaume Honore Kom
    View author publications

    You can also search for this author in PubMed Google Scholar

  4. Alain Bertin Tiedeu
    View author publications

    You can also search for this author in PubMed Google Scholar

Corresponding author

Correspondence to Justin Roger Mboupda Pone.

Ethics declarations

Conflict of interest

The authors declare that there are no conflict of interest regarding the publication of this paper.

Rights and permissions

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Mboupda Pone, J.R., Kamdoum Tamba, V., Kom, G.H. et al. Period-doubling route to chaos, bistability and antimononicity in a jerk circuit with quintic nonlinearity. Int. J. Dynam. Control 7, 1–22 (2019). https://doi.org/10.1007/s40435-018-0431-1

Download citation

  • Received:

  • Revised:

  • Accepted:

  • Published:

  • Issue Date:

  • DOI: https://doi.org/10.1007/s40435-018-0431-1

Keywords

Search

Navigation