High-resolution 3D weld toe stress analysis and ACPD method for weld toe fatigue crack initiation

Abstract

Weld toe fatigue crack initiation is highly dependent on the local weld toe stress-concentrating geometry including any inherent flaws. These flaws are responsible for premature fatigue crack initiation (FCI) and must be minimised to maximise the fatigue life of a welded joint. In this work, a data-rich methodology has been developed to capture the true weld toe geometry and resulting local weld toe stress-field and relate this to the FCI life of a steel arc-welded joint. To obtain FCI lives, interrupted fatigue test was performed on the welded joint monitored by a novel multi-probe array of alternating current potential drop (ACPD) probes across the weld toe. This setup enabled the FCI sites to be located and the FCI life to be determined and gave an indication of early fatigue crack propagation rates. To understand fully the local weld toe stress-field, high-resolution (5 μm) 3D linear-elastic finite element (FE) models were generated from X-ray micro-computed tomography (μ-CT) of each weld toe after fatigue testing. From these models, approximately 202 stress concentration factors (SCFs) were computed for every 1 mm of weld toe. These two novel methodologies successfully link to provide an assessment of the weld quality and this is correlated with the fatigue performance.

Introduction and background

Weld toe geometry

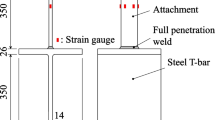
Stress-concentrating geometrical features inherent to welding are one of the primary causes of the low fatigue strengths of welded joints compared to the unwelded material. The stress-concentrating features can be broadly classified as macro- or micro-sized; the former considers the weld bead geometry as described by the plate thickness, leg attachment length and weld toe angle and radius (Fig. 1) whilst the latter considers weld toe flaws, which typically consist of undercuts and spatter. The role of the inherent flaws in fatigue crack initiation is similar to the behaviour of sharp notches in unwelded material [2] and it has been shown that [3] even in high-quality weld flaws can have depths of 0.1 mm.

Fig. 1

Schematic of the mathematically simplified geometry. (a) Global weld toe geometry; (b) local weld toe geometry; (c) flaw at weld-toe. Adapted from [1]

Due to the inherent inhomogeneity of welding processes, varying weld toe geometries can result, and it is currently not possible to economically identify and measure the inherent micro-size flaws [4,5,6]. Hence, a mathematically simplified or “perfect” weld toe geometry is assumed for weld toe stress and integrity assessments with the initial flaws being considered as initial cracks, with depth, a, and length 2c (Fig. 1).

To estimate stress concentration factors (SCFs) for simplified weld profiles, various parametric solutions can be found in the literature [7,8,9,10,11,12]. These are based on linear-elastic finite element modelling and are valid for specific ranges of geometrical parameters. Table 1 provides SCFs calculated for simplified weld toe geometries in the literature, with the four most recent works using a fictitious radius at the weld toe [14,15,16,17].

Table 1 SCF distribution obtained from simplified weld profiles

To capture the “true” weld toe geometry, a number of methods have been used in the literature: sectioning and microscopy, laser scanning and micro-computed tomography (μ-CT) (Table 2). Nykänen et al. obtained local geometrical parameters based on published experimental data and, by using LEFM, reported their influence on the fatigue behaviour of specimens similar to the ones used in this work [29]. Some of these studies further utilised the extracted geometry and computed linear-elastic weld SCFs from it; Table 3 provides the range of SCFs obtained for each study.

Table 2 Methods used for capturing the true weld profile

Table 3 SCF distribution obtained for true weld profiles

In Table 3, the maximum SCF values computed for “true” weld toe profiles are higher than the values obtained from the simplified weld toe profiles. This is primarily due to more stress-concentrating notch-like geometries being captured in the former, from either undulations in the weld bead or the inherent flaws such as undercuts.

Alternating current potential drop (ACPD) fatigue crack monitoring system

The basic premise of using a potential drop method (AC or DC) for crack growth monitoring can be found in [30, 31]. Essentially PD systems measure the electric impedance of the specimen when an excitation current is passed through it. Alternating current potential drop (ACPD) measures impedance as a function of the capacitive, inductive and resistive components, whilst DCPD measures only resistance. DCPD is the more conventional method used for fatigue crack propagation growth rate measurements [30], and a comparative study of the two techniques is provided in [32].

Okumura et al. 1981 [33] used ACPD for detecting crack initiation and monitoring crack extension during stable slow crack propagation. In this study, it was assumed that crack initiation occurred at the minimum PD signal and that subsequent increases in PD were related to crack extension. Venkatasubramanian and Unvala [34] discussed the use of ACPD for crack length measurements and highlighted the impact of the positioning and joining of current and voltage probes and leads, in addition to the influence of stress on ACPD. Gibson [35] also emphasised the impact of stress on the PD signal. Tests done by Raujol-Veillé et al. [25] used a digital ACPD system developed by MATELECT Ltd. to detect the size of fatigue cracks at the weld toe of their low alloy steel non-load carrying joints. A combination of both ACPD and DCPD has been used by Wojcik et al. [36] for creep damage monitoring and end of life warning for high-temperature components.

ACPD has been used in this study due to its characteristic “skin effect” [32, 34, 36], which causes the excitation current to flow close to the surface of the specimen, as opposed to flowing uniformly through the cross-section in DCPD. The distance of the current from the surface, called skin depth, is a function of the frequency of the alternating current, with the skin depth decreasing (i.e. closer to the surface) with an increase in frequency. This effect can be used to detect small surface breaking flaws or cracks initiating at the surface; it has been used for the latter in this work. The equipment used for this test is from the same manufacturer MATELECT Ltd. as in [25, 34,35,36].

Summary

The work presented in this paper describes the development of a process that combines state-of-the-art techniques available: to non-destructively resolve the “true” weld toe profile of non-load carrying welds, produce high-resolution weld toe SCF distributions and identify crack initiation under fatigue cycling using ACPD. This approach could lead to an evaluation of the effect of the “true” weld toe geometry on the fatigue performance of a good quality manual arc-welded joint using the fatigue notch strain approach [37]. However, this is beyond the scope of this paper and will be discussed in a future publication.

Methodology

Material and specimen

A structural C-Mn steel (complying to BS EN10025-2 S355 J2+N [39]) double-sided transverse non-load carrying joint of length 500 mm was manufactured by metal active gas (MAG) welding. For the work described in this paper, specimens of width 50 mm were extracted from the welded plate avoiding stop/start locations, the full dimensions of which are given in Fig. 2. Mechanical properties of the parent steel are provided in Table 4.

Fig. 2

(a) Micrograph of the specimen; (b) fatigue specimen geometry

Table 4 Mechanical properties of the base metal

Experimental methods

Multi-probe ACPD crack monitoring

One weld toe on the specimen was equipped with a series of ACPD probes to detect early fatigue crack initiation and monitor early fatigue crack growth. The remaining three weld toes were ultrasonically peened to delay fatigue crack initiation.

Load-control fatigue testing was carried out in tension at a load ratio (R) of 0.1, frequency of 5 Hz and stress range of 270 MPa in a Mayes servo-hydraulic test machine. A schematic of the test setup is shown in Fig. 3a, and an image of the specimen in the test machine is shown in Fig. 3b.

Fig. 3

(a) Schematic of specimen setup; (b) image of the specimen in the servo-hydraulic test machine

The multi-probe ACPD setup developed in this work utilised a MATELECT® CGM-7 ACPD Crack Growth Monitor. An array of “active” PD probe pairs was positioned along the weld toe with each probe pair positioned at 4 mm intervals and corresponding “reference” probe pairs were positioned 10 mm below each “active” pair in the parent metal (Fig. 4). Reference probes were used to account for changes in the test environment and setup that can influence the instantaneous PD readings, i.e. temperature and current dissipation. For this work, however, the data from the reference probes were not used in the analysis described in the next section. All the wires were twisted to minimise interference between them.

Fig. 4

Schematic of ACPD probes layout (not drawn to scale)

PD probes were made from enamelled nickel wires and were spot-welded to the specimen surface. Current wires were insulated copper wires and were connected to stud-welded nickel wire. Nickel wires were used as they provided the best stud weld connection with the steel specimen. Current wires were positioned along the surface of the specimen to allow for an effect called current focussing, which increases the density of the current field along the surface. This maximises the skin effect described in Section 1.2, and, therefore, the sensitivity of the technique for the detection of small fatigue cracks at the weld toe. A schematic of the arrangement is shown in Fig. 5 and an image in Fig. 6. An AC current of 2 A at a frequency of 20 kHz was used.

Fig. 5

Schematic of current wire layout (not drawn to scale)

Fig. 6

Specimen after ACPD wiring, ready for fatigue testing

The fatigue test was interrupted (stopped) after a target PD change of 2 mV at one “active” probe pair was observed. The value of 2 mV is based on the work of Raujol-Veillé [25] using MATELECT® ACPD crack growth monitoring equipment with an AC current of 1 A and a frequency of 20 kHz on a fillet weld. Raujol-Veillé used a single probe in his work and a change of 2 mV represented a weld toe crack depth of 500 μm. The work herein used a larger current to increase the sensitivity of the ACPD technique.

X-ray micro-computed tomography and finite element analysis

A 5 × 5 × 50 mm specimen consisting of the weld toe was extracted from the fatigue tested specimen using electrical discharge machining (EDM). The entire specimen was then scanned using non-destructive X-ray micro-computed tomography (μCT) at the University of Southampton’s μVIS Imaging Centre using the HMX system. Nine thousand seven hundred eight radiographs were generated during the scan, which were reconstructed in three dimensions (3D) using CT Pro 3D software. Scan parameters were determined from [1] and are given in Table 5. In terms of the impact of the surrounding weld bead geometry and base metal on the weld toe stresses, it has been seen before [1] that geometry beyond a distance of 2 mm has no significant impact.

Table 5 μ-CT scan settings

After 3D reconstruction, volumes were converted to a series of 2D images. These were cropped to the region of interest to reduce file size (Fig. 7a) and then processed in ImageJ® using the MinError(I) algorithm [38] (Fig. 7b). An algorithm was written in MATLAB® to extend each image, making it representative of the full weld bead (Fig. 7c and d).

Fig. 7

Image processing steps: (a) slice from the original CT volume; (b) processed image after using ImageJ auto-threshold tool; (c) additional processing in MATLAB to add material to the CT images; (d) final shape after image processing representative of the actual test specimen. The inset shows the true geometry in the final image

3D meshed models for finite element analysis (FEA) were created in Simpleware ScanIP™ software on image stacks of 150 image slices, equivalent to 0.73 mm of weld toe length. These sub-volume sizes were chosen to obtain feasible meshing times (approximately 2 h). The stack of binary images shown in Fig. 7d was imported into the software. A 3D rendered sub-volume is shown in Fig. 8 (for μCT scan resolution of 4.9 μm). The entire 3D volume was approximately 46.5 mm long, which gave 64 sub-volumes. Each such sub-volume was separately meshed and solved.

Fig. 8

3D sub-volume rendered in Simpleware scanIP™. The inset highlights the presence of the true geometry of the weld toe

A mesh validation study was performed to determine the optimum mesh density that accurately describes the local weld toe geometry whilst still providing feasible meshing times. Mesh refinement was applied at the weld toe using three concentric cylinders (Fig. 9). The remaining material was assigned a maximum element size of 1.5 mm. Adaptive meshing using the +FE Free algorithm in Simpleware scanIP™ was used to create the mesh.

Fig. 9

Mesh refinement zones in the form of three concentric cylinders, each of different element sizes. Cylinder 1 has the smallest elements, cylinder 3 the largest. In the overlapping sections, the element size of the internal cylinder is given precedence

Two kinds of mesh validation processes were performed:

• 1. Element size. In this mesh validation, the element size in cylinder 1, the refinement zone enveloping the weld toe along the weld bead, was varied to obtain convergence of SCF values obtained at the weld toe. The element size chosen was the same as the resolution of the μCT scan. Table 6 shows the results of this validation study.

Table 6 Mesh validation type 1—cylinder 1 element size

• 2. Cylinder 1 radius. In this mesh validation, the radius of cylinder 1 was varied. It was seen that a radius of 0.2 mm gave feasible meshing time (approximately 2 h) and convergent SCF results. Table 7 shows the results of this validation study. Note that the meshing time varies for each sub-model, depending on the complexity of the geometry in each model.

Table 7 Mesh validation type 2—cylinder 1 radius

Based on these two types of mesh validation studies, the final mesh parameters were decided and are presented in Table 8. Figure 10 shows the final meshed weld toe geometry for one sub-volume containing a cold lap feature. This mesh contains a total of 8.7 million elements and 1.5 million nodes.

Table 8 Final mesh refinement parameters

Fig. 10

Final meshed sub-volume containing a cold lap feature at the weld toe

FE models (without sub-modelling) were created in ABAQUS® using the orphan meshes exported from Simpleware scanIP™. Boundary conditions were applied to the model to replicate the fully tensile fatigue test setup. A 3D static linear-elastic stress analysis was carried out for each of the 64 sub-volumes to obtain the stress distribution along the weld toe. Young’s modulus of 207 GPa and Poisson’s ratio of 0.3 were used for the stress analysis. As the stress analysis was purely linear-elastic, no hardening effects and phase transformation effects were considered. Due to the size of the models, all computing was performed on a high-performance computing cluster facility at the University of Southampton.

Results and discussion

3D FE modelling

Weld toe SCFs were extracted from each FE model at 5 μm and 50 μm intervals using an algorithm developed in MATLAB. Two SCFs were extracted: SCF₁₁, the maximum SCF in the x-direction (longitudinal to the parent metal) and SCF_PS, the maximum SCF in the principal stress direction. Example stress distributions from four sub-models exhibiting different geometries and stress distributions are shown in Fig. 11. Regions with SCFs below 1.0 are grey and SCFs above 4.0 are dark red; all images have the same scale.

Fig. 11

Example SCF₁₁ distributions from four sub-models—(a) and (b) are examples with relatively lower stress concentration; (c) example of a cold lap defect; (d) example of a weld bead section with consistently large stress concentration across the weld toe

Maximum SCF₁₁ and SCF_PS values for the length of weld toe studied here (46.5 mm) are plotted in Fig. 12 at 5 μm intervals. The maximum values are plotted as there are multiple values of stress in any particular plane. The ACPD probe distribution along the weld toe has also been shown in the image. Over 9300 SCF values were obtained and statistically analysed to give the mean, median, range, interquartile range and standard deviation for the welded sample (Table 9). A box-whisker plot showing the SCF₁₁ distribution is plotted in Fig. 13.

Fig. 12

SCF₁₁ and SCF_PS values plotted along the length of the weld toe

Table 9 Statistical analysis of the SCF values obtained

Fig. 13

Box and whisker plot for maximum SCF₁₁ distribution

ACPD fatigue crack initiation monitoring

The interrupted fatigue test was performed to 84,344 cycles, which corresponded to a PD drop of 4 mV at Probe 5. PD drops (between 0.5 and 2 mV) were observed at six of the other twelve PD probes; no PD drops were observed at the remaining five PD probes. To represent this data graphically, the absolute potential drop (PD) value detected by the probes is presented in Fig. 14 in millivolts (mV). Crack initiation life was evaluated based on the onset of PD drop in Probe 5. It is important to highlight that crack initiation life has been defined as the number of fatigue cycles to crack growth of a certain crack length or depth, also referred to as a technical crack [37]. In this work, however, crack initiation life is defined by the indication obtained from the ACPD fatigue crack growth monitoring technique.

Fig. 14

ACPD data for selected probes along with the point of initiation in the overall life of the specimen

Serial metallography results

Further validation of the work described thus far is provided by serial metallography. This was conducted at regions of interest along the weld toe to capture the crack depth and morphology to understand if it related well with the FE and ACPD results. A controlled metallography methodology was developed to remove material transverse to the weld toe at 50 μm and 200 μm intervals. The sections provided information on fatigue crack depth, crack morphology and the number of cracks. Figure 15 features four such obtained sections. Figure 15(a) shows a fatigue crack with bifurcation occurring possibly around grains. Figure 15(c) shows a fatigue crack at an overlap defect at the weld toe. Figure 15(d) shows the presence of three fatigue cracks that are growing on two different planes adjacent to each other. A total of 180 sections have been taken at regions of interest, to cover a total of approximately 18 mm of the total weld toe length of 46.5 mm. The crack depths of nine different cracks are represented along with the SCF₁₁ distribution plot in Fig. 16. 7.2.C, 7.3.SH.C and 7.3.LO.C represent the mounts into which the specimen was cut for serial metallography. The number after “.C” (for example 1 in 7.2.C1) represents the serial number of the crack. Results from this plot will be further analysed in Section 3.4.

Fig. 15

Sections with different features—(a) fatigue crack exhibiting bifurcation located at the weld toe; b) expected fatigue crack growth–transverse to the stress axis; (c) fatigue cracking from an overlap defect at the weld toe; (d) two fatigue cracks which eventually coalesced in further sections

Fig. 16

Observed crack morphology and depths from serial metallography

Validation of 3D finite element linear-elastic stress analysis using ACPD and serial metallography

Figure 16 presents the observed crack depth at regions identified using the ACPD probe data in Fig. 14. Multiple cracking was observed at the weld toe. Figure 17 contains two higher resolution plots from Fig. 16 and are the regions subjected to serial metallography. Some smaller cracks, with depths between 5 and 50 μm and lengths (along the weld toe for which the crack was observed) between 20 and 200 μm, were removed from the plots for clarity. The deepest cracks are in the regions with the maximum change in ACPD data. This area also corresponds to the area of consistently larger SCF₁₁ observed in the FE analysis. It corresponds to a location where two weld ripples meet to create a region of stress-concentrating geometry. Crack depth is seen to follow the SCF distribution. However, the ACPD probes P2 and P3 have not shown the same degree of change as probes P4, P5 and P6. This could be due to the fact that the SCF distribution at P2 was lower than P5. No serial metallographic evidence is available for P3. Also, P6 experienced multiple cracking, which could explain the deflection in measured PD voltage. The effects of stress on ACPD potentially play a role as well, and further testing would be required to investigate the exact effects. It is also important to note that fatigue crack initiation is not always associated with regions of higher SCFs, but also occurs at surface spatter which exhibited SCF₁₁ from 3.00-6.40.

Fig. 17

Plots A and B represent the crack depth with SCF₁₁ distribution for the regions that have been subject to serial metallography

Fatigue cracking (revealed from serial metallography) has occurred at the locations of high stress concentration observed in the 3D FE stress analysis. The ACPD probes information used to indicate fatigue crack growth location and life have further validated this.

Discussion

The multiple probe ACPD system captured early fatigue crack propagation at the weld toe and indicated the location of fatigue crack initiation. This gives the potential of focussing on the crack initiation sites at the weld toe in future tests, and to obtain more information on the most critical weld toe geometries to fatigue. The qualitative data obtained from continuous ACPD monitoring also correlated well with the obtained SCF₁₁ values and crack depths measured from serial metallography. The correlation to crack depths indicated that the ACPD signal is also likely to be influenced by multiple cracking and neighbouring cracking and net section stresses.

The high (elastic) SCF values obtained in this work are larger than most of those obtained in previous similar studies in the literature [14,15,16,17,18,19, 21, 28]. This could be attributed to both the methods used for capturing the weld toe geometry and the resolution. Some measurement methods such as laser scanning are unable to capture notch-like flaws when paint is applied to the surface prior to scanning and many notch-like flaws observed in this work were smaller than some of the resolutions used in previous studies (Table 3). Higher SCFs up to 12.00 were captured in a previous study that used μ-CT and 2D FE stress analysis on similar arc-welded joints [1]. Interestingly, the welds studied had larger flaws than those in this work, herein flaws of depths up to 40 μm were observed whilst in [1], flaws up to 200 μm in depth were observed.

Conclusion

• In this study, the weld toe profile has been resolved using μ-CT at a resolution (< 5 μm) capable of capturing the inherent flaws. The 3D volumes have then been subjected to a high-resolution FE stress analysis, the results of which have been linked to fatigue crack initiation and early crack propagation data obtained from the joint using a multiple probe ACPD method.

• SCF₁₁ values ranging between 2.03 and 8.49 were obtained for the weld studied in this work, which resulted in fatigue crack depths up to 230 μm after 84,344 cycles at a stress range of 270 MPa and stress-ratio of 0.1. SCF₁₁ values correlated well with ACPD data and measured crack depths from serial metallography, and the results indicated that multiple cracking is likely to influence the ACPD results though the data still provides a clear indication of crack initiation below 0.25 mm.

• The methodology developed in this work provides a data-rich weld toe analysis method capable of linking the “true” weld toe stresses with fatigue crack initiation results and thus allowing for an improved assessment of welded joints in the future.