1 Introduction

Welding is a technology that melts a material and filler metal by the plasma arc. The surface shape and the penetration shape are deformed by the influence of four types of convections, as shown in Fig. 1. The four types of convections interact with each other. As a result, complicated flow will occur in welding pool. In welding pool, the heat energy is transported by the flow, and the shape of the welding pool changes [1]. For example, in the case of a strong outward convection, the heat energy will be transported for outside, and the weld penetration becomes shallow and wide. In contrast, in the case of a strong inward flow, the heat energy will be transported along the depth direction, and the weld penetration becomes narrow and deep. Therefore, the shape of the bead and penetration of the weld zone can significantly affect the mechanical performance of a joint, and hence, predicting the shape created by welding is essential. However, prediction via conventional computational fluid dynamics is difficult because the melting section is deformed greatly by arc affect and convections.

Fig. 1
figure 1

Convection in a welding pool

Full size image

On the other hand, the moving particle semi-implicit (MPS) method developed by Koshizuka [2–4] expresses fluid flow as a collection of particles. This facilitates the calculation of large deformations, free surfaces, and the breakup or union of fluids.

However, many other particle methods such as smoothed particle hydrodynamics (SPH) and molecular dynamics (MD) are currently available. SPH can be used for various problems, but the governing equation is difficult and computationally expensive. MD is also very useful; however, molecular behavior is determined on a nanoscale. The size of the welding area varies from millimeters to meters, and hence, MD calculations are unsuitable for the simulation of welding. If welding simulations are to be used in the production field, then simple and fast calculations are required. The MPS method is easy to use and requires less computational effort than other particle methods. Therefore, we believe that the MPS method is well suited for the analysis of welding.

In this study, we determine the forming mechanism of a welding pool. To determine welding pool phenomena, we developed an MPS method that incorporates a thermal conduction model, heat transfer and radiation model, melting and solidification model, and surface tension model. However, determining both the welding arc and welding pool phenomena using the MPS method is difficult because it is extremely time consuming and has high calculation cost. As such, welding arc analysis is performed using the lattice-based Finite Volume Method (FVM). To reduce computational cost, welding arc data are then used by the MPS method as boundary conditions or source calculations. In this study, we describe the addition of a physical model to the MPS method and report the results of the welding pool analysis.

2 Moving particle semi-implicit

2.1 Moving particle semi-implicit

In this study, we use the MPS method developed by Koshizuka [2–4] to perform an incompressible flow analysis. We also use the program code provided by the “MPS Code User Group.” The momentum equation of an incompressible fluid is given as

$$ \frac{Du}{Dt}=-\frac{1}{\rho}\nabla P+\upsilon {\nabla}^2u+g+{F}_s+{F}_{ma}. $$
(1)

Here, u, ρ, P, ν, g, F s , and F ma are the velocity, density, pressure, kinematic viscosity, gravity, surface tension, and Marangoni force, respectively. Equation (1) includes both gradient and Laplacian differential operators. These operators are discretized by the particle interaction model of a common MPS method.

Equation (1) is discretized using a numerical model for Laplacian and gradient operators; this model considers the interaction between the particles. The gradient differential operator is given as

$$ {\left\langle \nabla \varphi \right\rangle}_i=\frac{d}{n^0}{\displaystyle \sum_{j\ne i}\left[\frac{\varphi_j-{\varphi}_i}{{\left|{r}_j-{r}_i\right|}^2}\left({r}_j-{r}_i\right)w\left(\left|{r}_j-{r}_i\right|\right)\right]}. $$
(2)

The Laplacian differential operator is given as

$$ {\left\langle {\nabla}^2\varphi \right\rangle}_i=\frac{2d}{n^0\lambda }{\displaystyle \sum_{j\ne i}\left[\left({\varphi}_j-{\varphi}_i\right)w\left(\left|{r}_j-{r}_i\right|\right)\right]}. $$
(3)

Here, φ is a physical quantity, d is the number of dimensions, n 0 is particle number density at the initial condition of a disposed particle, r is the position of the particle, and w is the weight function. The weight function w varies with the distance between the calculated particle and surrounding particles. The effect of the surrounding particles is considered by the weight function w when their interaction with the calculation particle is determined. Moreover, particle i refers to the calculated particle whose number density n i is defined as follows [2–4]:

$$ w(r)=\left\{\begin{array}{ll}\frac{r_e}{r}-1\hfill & \left(0\le r\le {r}_e\right)\hfill \\ {}0\hfill & \left({r}_e\le r\right)\hfill \end{array}\right., $$
(4)
$$ {n}_i={\displaystyle \sum_{j\ne i}w\left(\left|{r}_j-{r}_i\right|\right)}. $$
(5)

Here, r e is the effective radius. The effect of other particles on the effective radius of particle i is considered in the calculation; r is the distance between particles i and j, and r i and r j are their respective positions. Furthermore, particles j are the particles surrounding particle i in a volume of effective radius r e .

λ is a parameter used for normalization in Laplacian model and is given as follows:

$$ \lambda =\frac{{\displaystyle \sum_{j\ne i}{\left|{r}_j-{r}_i\right|}^2w\left(\left|{r}_j-{r}_i\right|\right)}}{{\displaystyle \sum_{j\ne i}w\left(\left|{r}_j-{r}_i\right|\right)}}. $$
(6)

The momentum and energy equations are determined from Eqs. (2)–(6).

A temporary velocity is calculated and used to determine the gravity and surface tension terms via an explicit calculation; the velocity is then corrected by a pressure equation. The particle number density is changed by the temporary velocity. This density is proportional to that of the material. In fact, instead of using the material density, pressure can be described in terms of the initial particle number density n 0 and temporary particle number density n *.

$$ {\nabla}^2{P}^{k_n+1}=-\frac{\rho_0}{\varDelta {t}^2}\frac{n*-{n}^0}{n^0}. $$
(7)

Here, k n is the time step of the calculation. The momentum equation is formulated as follows. First, the gravity and surface tension terms are calculated by an explicit method. Second, the viscosity term is determined by an implicit method and is used to calculate the stable high-viscosity fluid flow. Third, after moving the particle temporarily, the Poisson equation of pressure is formulated using an implicit method. However, the particle method results in unrealistic pressure oscillations at high frequencies. Therefore, we used the suppression method developed by Kondo and Koshizuka [5] to suppress these oscillations. Other calculations were performed as described in references [2–4].

2.2 Analysis model of thermal conduction, melting, and solidification

A law of energy conservation must be incorporated in the modeling of thermal conduction, melting, and solidification. This conservation of energy is given as follows:

$$ \frac{Dh}{Dt}=k{\nabla}^2T+Q, $$
(8)

Here, h, T, k, and Q are the enthalpy (energy per unit volume), temperature, thermal conductivity, and total amount of heat, i.e., the sum of heat input and radiation, respectively. Heat is input when Q > 0 and radiated when Q < 0. The first term on the right is discretized by the Laplacian of the MPS method, and the thermal conduction is calculated.

In this study, enthalpy at the position of a particle is calculated, and temperature is subsequently determined using Eq. (9). The temperature does not change while changing phase because it is influenced by latent heat.

$$ {T}_i=\left\{\begin{array}{ll}{T}_m+\frac{h-{h}_s}{\rho {C}_{Ps}}\hfill & \left(h<{h}_s\right)\hfill \\ {}{T}_m\hfill & \left({h}_s<h<{h}_l\right)\hfill \\ {}{T}_m+\frac{h-{h}_l}{\rho {C}_{Pl}}\hfill & \left(h>{h}_l\right)\hfill \end{array}\right.. $$
(9)

Here, T i is the temperature of the particle, T m is the melting temperature, h s is the enthalpy at the start of melting, and h l is the enthalpy at the end of melting; C Ps and C Pl are the specific heat of solid and liquid, respectively. In this study, heat loss by the vaporization of the molten metal is not considered in the simulation.

The quantity of heat Q is defined as the sum of radiation q o , heat transfer q c , and heat input q i .

$$ Q={q}_o+{q}_c+{q}_i. $$
(10)

The amount of radiation q o is calculated using Eq. (11):

$$ {q}_o=-\varepsilon \sigma \left({T}^4-{T}_a^4\right){S}_i. $$
(11)

Here, ε, σ, T, and T a are the radiation ratio, Stefan–Boltzmann constant, temperature in the heated region, and surrounding temperature, respectively. In this study, T a is 300 K because the heat input is calculated by the arc simulation using the lattice method. If the heat input at the temperature of the atmosphere T a is used, then the heat input will be counted twice. To avoid this double count, only heat emission is considered in Eq. (11), and the temperature of the atmosphere is considered to be 300 K.

S i is the surface area of particle i. In the particle method, the surface area varies with the particle number density. The interparticle spacing r 0 of cubic particles is equal to the length of each side of the cube. S i is calculated using Eq. (12):

$$ {S}_i=\left(1-\frac{n_i}{n^0}\right){N}_s{r}_0^2. $$
(12)

Here, n 0 is the initial particle number density, n i is the current particle number density of particle i, and N s is the number of surface areas. For example, N s is 4 for two-dimensional (2D) calculation and 6 for three-dimensional calculation. If n i is 0 when there is nothing around particle i, then the surface area is N s r 0 2. If n i is n 0, corresponding to the density of the material, then the surface area is 0. Particles placed on the corner of the cube have surface areas of 0–N s r 0 2, which are determined via interpolation.

In addition, convection heat transfer q c is calculated from heat transfer coefficient α and Newton’s law of cooling.

$$ {q}_c=\alpha \left({T}_m-{T}_a\right). $$
(13)

The solid rate γ is defined as the rate of solid and liquid in particles and is calculated from the enthalpy [2] using Eq. (14) to calculate melting and solidification and to determine the phase of a material.

$$ \gamma =\left\{\begin{array}{ll}1\hfill & \left(h<{h}_s\right)\hfill \\ {}\frac{h_s-h}{h_l-{h}_s}\hfill & \left({h}_s<h<{h}_l\right)\hfill \\ {}0\hfill & \left(h>{h}_l\right)\hfill \end{array}\right.. $$
(14)

Therefore, the material is completely solid when γ is 1 and liquid when γ is 0. If γ is neither 0 nor 1, the material is a mixture of solid and liquid. Moreover, reciprocal average is used for determining the thermal conductivity k of this mixed state because generally thermal conductivity k is different from liquid and solid [6].

$$ \frac{1}{k}=\frac{\gamma }{k_s}+\frac{1-\gamma }{k_l}. $$
(15)

Here, s and l indices denote solid and liquid, respectively.

The kinematic viscosity, thermal conductivity, and specific heat are determined from table of temperature values. The values between each temperature are interpolated and used for the calculation of the particle.

Thermal conduction, melting, and solidification are calculated after being added to the computational algorithm of the MPS code. In this study, the temperature, melting, and solidification are calculated after solving the momentum equation and determining the motion of the particles.

2.3 Surface tension and Marangoni force

The improved potential model proposed by Ito et al. [7] is used to calculate the surface tension. The equation given below is used to calculate potential applied between particles.

$$ \varPhi (r)=C\varphi (r), $$
(16)
$$ \varphi (r)=\left\{\begin{array}{ll}-\frac{1}{3}\left(r-\frac{3}{2}{r}_0+\frac{1}{2}{r}_e\right){\left(r-{r}_e\right)}^2\hfill & \left(r<{r}_e\right)\hfill \\ {}0\hfill & \left(r\ge {r}_e\right)\hfill \end{array}\right.. $$
(17)

Here, C is the coefficient of the potential function, and r 0 is the initial distance between the particles. The potential force F i po exerted by particle j on the effective radius of particle i is calculated from Eq. (19).

In Eq. (16), considering relations of C and surface tension coefficient σ is necessary because the potential coefficient C is unknown. However, the surface tension coefficient σ is equivalent to the energy saved in the surface per unit area. If the energy needed to create the surface is calculated, the relation between the energy and surface tension can be derived. When we divide a particle of diameter l 0 into two surfaces, each with a surface area of l 0 2, then the energy is calculated from the equation as follows:

$$ 2\sigma {l}_0^2=\varPhi (r). $$
(18)

If the surface tension coefficient σ is known, then the potential coefficient C can be determined from Eqs. (16)–(18).

$$ {F}_i^{po}={\displaystyle \sum_j\frac{\partial \varPhi \left(\left|{r}_j-{r}_i\right|\right)}{\partial \left|{r}_j-{r}_i\right|}\frac{r_j-{r}_i}{\left|{r}_j-{r}_i\right|}}. $$
(19)

The potential force results in an attraction between the particles. However, forces of repulsion are also exerted from inside the fluid. The surface tension is modeled as the total force of attraction between the particles and repulsion from inside the fluid and is defined as follows:

$$ {F}_i={\delta}_s\frac{ \cos {\theta}_i}{{ \sin}^3{\theta}_i}{F}_i^{po}. $$
(20)

Here, θ i is an angle between particle i and other particle, as shown Fig. 2. δ s is constant. It is assumed that the surface tension affects only the outermost surface particles. However, particles that are designated as surface particles are frequently located at depths of two or three times that of the particle radius, away from the surface. To affect only the outermost surface particles, a correction coefficient δ s is used. In this study, δ s  = 0.4 was used for the calculations because this value led to more stable results than other values tested.

Fig. 2
figure 2

Schematic showing the angle θ

Full size image

We also added a wettability model such as that proposed by Ito et al. [7]; this model considers the wettability of the fluid.

The Marangoni force is a surface force that results from the temperature-dependent coefficient of the surface tension. In this study, the model developed by Koshizuka et al. [7] was used to calculate the Marangoni force using Eq. (21). Thus, the surface tension coefficient is proportional to the potential coefficient C, and the Marangoni force is determined as changes in the latter with the former, as defined in Eq. (22).

$$ {F}_i^{ma}={\delta}_m{\displaystyle \sum_j\left({C}_j-{C}_i\right)\frac{\partial \varPhi \left(\left|{r}_j-{r}_i\right|\right)}{\partial \left|{r}_j-{r}_i\right|}}\frac{r_j-{r}_i}{\left|{r}_j-{r}_i\right|}, $$
(21)
$$ {C}_i=\frac{\sigma_i\left({T}_i\right)}{\sigma_0\left({T}_0\right)}{C}_0. $$
(22)

Here, C i and C j are the potential coefficients of particles at the fluid surface, and C 0 is the standard potential coefficient calculated from the surface tension coefficient σ 0(T 0) at temperature T 0. As Eq. (22) shows, C i depends on the temperature of each particle, standard potential coefficient C 0, surface tension coefficient at room temperature σ 0(T 0), and surface tension coefficient at each particle temperature σ i (T i ). δ m is constant, and δ m  = 0.4 is was used for the calculations because this value led to more stable results than other values tested.

2.4 Arc force

The effect of the arc force calculated by the FVM using Tanaka’s arc model [1] is considered in the MPS method as a boundary condition. In the arc calculation, two types of boundary conditions are applied at the surface of the base material, i.e., if the base material is solid, then its surface is considered as a wall, and the velocity of the solid area is zero. However, if the base material is liquid, then its surface is considered as fluid, which has the same density and viscosity as the base metal.

The node position and arc conditions (velocity and pressure) at each node calculated by the FVM are used as the background lattice in the particle method calculation. Figure 3 shows a schematic of the particle positions and background lattice. In Fig. 3, the red, yellow, and gray circles represent surface, liquid, and solid particles that are affected by the arc flow, move freely, and immobile, respectively.

Fig. 3
figure 3

Schematic of the position of the background lattice

Full size image

The pressure was calculated by the MPS method using the Dirichlet boundary condition in which a pressure of zero was assigned to the outermost surface particle. However, the calculated arc pressure was applied to the outermost surface particle.

The velocity of the fluid flow is then fixed in space; because this calculation incorporates one-way coupling, the calculated velocity does not consider the shape of the welding pool surface. Therefore, the effect of the arc is reduced when the surface of the welding pool moves large distances from the background lattice. This reduced arc effect results in a rise in the surface of the welding pool. However, if the surface of the molten pool rises and the arc effects are increased, then the surface of the welding pool moves toward the arc again. This results in an instability in the welding pool behavior, and the calculation becomes unstable.

To avoid this instability, a background lattice is superimposed on the initial surface. This background lattice affects particles near the surface. In addition, changes in the shape of the surface are considered during the calculation.

As Fig. 4 shows, the flow velocity resulting from the welding arc and pressure is interpolated for particles at the surface of the background lattice because the arc force acts only on the surface of the welding pool. The velocity is calculated using the equations as follows.

Fig. 4
figure 4

Schematic of the interpolation between particles

Full size image
$$ \left\{\begin{array}{l}{V}_a=\left({V}_2-{V}_1\right)\frac{x_i-{x}_1}{x_2-{x}_1}+{V}_1\\ {}{V}_b=\left({V}_4-{V}_3\right)\frac{x_i-{x}_1}{x_2-{x}_1}+{V}_3\end{array}\right., $$
(23)
$$ {V}_i=\left({V}_b-{V}_a\right)\frac{y_i-{y}_1}{y_2-{y}_1}+{V}_a. $$
(24)

Here, x 1–2 and y 1–2 are the positions of nodes 1–4 in Fig. 4; x i and y i are the positions of particle i; V 1–4 is the value at nodes 1–4; V a and V b are the interpolation values along the x axis; and V i is the value resulting from the interpolation of particle i. The pressure term is usually calculated using the Dirichlet boundary condition in which a pressure of zero is assigned to the surface particles. The arc pressure is the only input pressure used in this study.

The shear force at the surface of the welding pool results from the viscosity between the arc flow and surface of the welding pool. Moreover, the arc flow induces a drag on the pool. In a 2D calculation, the velocity u * liquid resulting from the arc force is determined from Eq. (25); u arc and u k liquid are the fluid velocity resulting from the welding arc and convection velocity of the welding pool, respectively.

$$ {u}_{\mathrm{liquid}}^{*}=\frac{\rho_{\mathrm{gas}}}{\rho_{\mathrm{liquid}}}\nu \frac{\left({u}_{\mathrm{arc}}-{u}_{\mathrm{liquid}}^k\right)}{r_0}\varDelta t. $$
(25)

The density ratio ρ gas/ρ liquid is used to account for the fact that gas and liquid have differing densities; ρ gas and ρ liquid are the respective densities of the arc plasma and molten metal, ν is the kinematic viscosity of the plasma, r 0 is the initial distance between the particles, and Δt is the time increment. Equation (25) is calculated explicitly before solving the Poisson equation of pressure, and u * liquid is defined as a virtual velocity of the particles.

3 Validation of thermal model

3.1 Thermal conduction

The thermal calculation inserted in the MPS method was validated. One-dimensional (1D) unsteady thermal analysis was performed at a plate to validate the thermal analysis performed via the MPS method. Equation (26) was used to determine the 1D unsteady thermal conduction and was formulated to compare the results thereof with those obtained from the MPS method. Figure 5 shows a schematic illustration of the system used in this calculation. The temperatures of the iron plate and side surface were set to 300 and 500 K, respectively. The upper and bottom sides were set as the insulation boundary. In addition, the 1D temperature distribution at the center of the plate obtained via calculation from Eq. (26) was compared with the analytical solution.

Fig. 5
figure 5

Schematic of the region considered in the calculation. The hatched and central regions denote the high-temperature side surface and low-temperature iron plate, respectively

Full size image
$$ \frac{T}{T_0}=\frac{4}{\pi}\left\{ \exp \left(-{\pi}^2\frac{at}{L^2}\right) \sin \frac{\pi x}{L}\right.\left.\frac{1}{3}+ \exp \left(-{\left(3\pi \right)}^2\frac{at}{L^2}\right) \sin \frac{3\pi x}{L}+\cdot \cdot \cdot \right\}. $$
(26)

Here, T, T 0, a, π, t, L, and x are the temperature, initial temperature, thermal diffusivity, circular constant, time, thickness of iron plate, and position of calculation point. The material-temperature-dependent shift in thermal properties was not considered in this calculation. Table 1 lists the properties of the iron plate.

Table 1 Properties of the iron plate used in the thermal conduction calculation
Full size table

The temperature distributions obtained after t = 300 s were compared. Figure 6 shows the temperature distributions and corresponding graph of the analytically determined solution and the result of the MPS method. The maximum deviation between the results was 1.5 %. Furthermore, the thermal conduction was accurately modeled by the MPS method.

Fig. 6
figure 6

The result of the MPS calculation and comparison of the 1D temperature distribution. a The MPS results are color coded according to temperature; b 1D temperature distribution obtained after 300 s. The red and blue lines denote the MPS and analytically determined results, respectively

Full size image

3.2 Heat transfer and radiation

Heat transfer was validated by investigating the cooling process of a stainless steel plate. Table 2 lists the material properties of the stainless steel used for the calculation performed under the assumptions of air atmosphere. The coefficient of heat transfer is calculated by considering natural convection. Figure 7 shows a schematic of the calculation region. Temperature was also calculated using ABAQUS and compared at points 1–4 in Fig. 4.

Table 2 Parameters used in the calculation of heat transfer and radiation
Full size table
Fig. 7
figure 7

Schematic of the calculation model. The size of the calculation model was 1/4th that of 110 mm × 74 mm × 11 mm (i.e., the hatched area)

Full size image

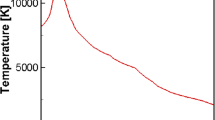
Figure 8 shows the result of the investigation of the cooling process at each point for 60 s. The temperatures calculated for the 60 s were compared, and a maximum deviation of 5 % was obtained between the MPS and ABAQUS results. Furthermore, deviations of 2 and 5 % were obtained in the case of points 1 and 2 that were placed at the center and edge of the top surface, respectively. The MPS result revealed a tendency for faster cooling than ABAQUS. The same element size was used in both calculations. However, the respective surface areas of the ABAQUS and MPS models were calculated as that corresponding to a square and the particle number density. Thus, the surface in the former calculation was slightly larger than that of the latter.

Fig. 8
figure 8

Result of the cooling process of stainless steel showing temperature plotted as a function of time. Results from the ABAQUS and MPS calculations are plotted as solid lines and symbols, respectively

Full size image

3.3 Convection of buoyancy

Buoyancy results from a temperature difference, and natural convection occurs in a fluid. A thermal cavity was determined to verify the convection of buoyancy, and the results were compared with those obtained using the FVM described by Davis [8]. Figure 9 shows a schematic illustration of the thermal cavity. The Rayleigh number (Ra) was changed by varying the temperature of the high-temperature side; the temperature of the low-temperature side was set to zero. Ras of 103, 104, and 105 were used in the calculation; Table 3 lists the properties of the thermal cavity considered.

Fig. 9
figure 9

Schematic of the thermal cavity. The area surrounded by the wall. One side of the wall is fixed at a high temperature and the other at 0 K

Full size image
Table 3 Properties of the thermal cavity used in the calculation
Full size table

Figure 10 shows one of the results obtained for Ra = 103 and reveals a close (qualitative) correspondence between the flow line and temperature distribution of the MPS method and FVM. To compare the results quantitatively, the maximum velocity associated with each Ra result was converted to a dimensional-less variable. With this non-dimensional variable, deviation (error values) of 6, 15, and 8 % were obtained between the MPS and FVM results for Ra = 103, 104, and 105, respectively.

Fig. 10
figure 10

Comparison of a flow line and b boundary temperature. The temperature lines were superimposed on the MPS result

Full size image

3.4 Melting and solidification

The solidification of water was investigated to validate the implemented melting and solidification model. A 79 mm × 79 mm area was filled with water of 0 °C, which was solidified from the exterior to interior by cooling the outer wall at a rate of 0.085 °C/min. Table 4 lists the parameters used in the calculation. This problem was examined experimentally by Saitho [9]. The present calculation was based on the assumption that water flow and heat transfer did not occur. The temperature of the water was set to zero, and the thermal conductivity of ice was used for the calculation because thermal conduction occurred only between the ice and water.

Table 4 Parameters used in the solidification calculation
Full size table

Figure 11 reveals a close correspondence between the calculated and experimental results for the center of each side of the cavity. However, the boundary shape at the corner was round in the case of the latter than the former. This indicates that the boundary in the MPS method had a lower cooling ratio than that in the experiment. According to Saito et al., the temperature decreases readily at the corner of the region. However, the tendency for temperature decrease was not considered in this calculation.

Fig. 11
figure 11

The results of solidification showing the boundary between the water and ice after 20, 40, and 60 min. The symbols and solid lines denote the results of the MPS calculation and experiment by Saitho, respectively, for a the entire region and b part of the corner

Full size image

4 Analysis of arc welding

4.1 Conditions

The MPS method was used to calculate the welding pool in 2D, and the arc flow was considered. Furthermore, the stable TIG arc was determined by the FVM and then by the particle method. The parameters used for the arc determination included current, Ar gas flow rate, arc length, cathode tip angle, base metal, and cathode material of 200 A, 10 L/min, 5 mm, 60°, pure iron, and tungsten, respectively. The results of the calculation were output at each node. These data were then used for the particle method calculation. The approximated heat input was proportional to the distance from the center of an arc to the surface particles. Figure 12 shows the distribution of heat input; Fig. 13 shows the 2D model of the particles from the iron plate. In addition, Table 5 lists the parameters used in the calculation, and Fig. 14 shows the temperature dependence of the surface tension. The surface tension of pure iron had a negative temperature coefficient. For comparison, we also performed the calculation for a positive temperature coefficient.

Fig. 12
figure 12

Distribution of the input heat energy

Full size image
Fig. 13
figure 13

Schematic of the calculation model of the particle method

Full size image
Table 5 Parameters used in the weld pool calculation
Full size table
Fig. 14
figure 14

Temperature dependence of the surface tension

Full size image

5 Results and discussion

Figures 15 and 16 show the calculation result and velocity vector, respectively.

Fig. 15
figure 15

Result of the welding pool analysis with the arc force color coded according to temperature for a negative and b positive temperature coefficients of surface tension

Full size image
Fig. 16
figure 16

Distribution of the vector for a negative and b positive temperature coefficients of the surface tension. The arrow length denotes the magnitude of the velocity

Full size image

As Fig. 15 shows, the surface tension acts in the direction of low temperature, and outward convection was induced with the arc flow. The weld penetration became wide and shallow with heat transfer to outside via an outward flow. However, as Fig. 15b reveals, the positive surface tension acts in the direction of high temperature, thereby inducing inward convection. The resulting heat transferred in the through-thickness direction by an inward flow, and the weld penetration became narrow and deep.

As Fig. 16b shows, the outward flowing arc stream is located at the surface. There is also a strong inward convection, although the velocity of the Marangoni convection is significantly smaller than the arc velocity. This stems possibly from an underestimation of the arc force defined in Eq. (25). Moreover, the influence of the arc flow should change with the deformation of the welding pool surface, and the model must be adapted or a new model must be developed to take this into consideration.

The actual material has, in fact, a negative surface tension coefficient. The result obtained using the negative coefficient was compared with the experimental result; the melting shape resulting from the MPS calculation was more than that from the experiment. This may be attributed to the thermal energy that remained in the welding pool because the input heat could not move to the front or back sides of the 3D model. Further investigation is required to explain the aforementioned difference in shape.

6 Conclusions

We developed an MPS method for modeling welding effects. This method allows the representation of a free surface, clear boundary shape, and easily calculated phase shifts.

  1. 1.

    To calculate the heat effect, we added a heat conduction model and a melting and solidification model to the MPS method. Surface tension and Marangoni force models were also added to determine the surface tension and Marangoni convection.

  2. 2.

    The effect of arc flow calculated by Tanaka’s model is considered by using the one-way coupling model.

  3. 3.

    The calculated welding pool was shallow and exhibited wide penetration for a positive temperature coefficient of the surface tension. In contrast, the welding pool was deep and exhibited narrow penetration for a negative temperature coefficient of the surface tension. The tendency for the deformation of the welding pool was determined by the developed MPS method.