AC impedance spectroscopy and conductivity studies of Dy doped Bi₄V₂O₁₁ ceramics

Abstract

The ac impedance and conductivity properties of Dy doped Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) ceramics prepared by solid-state reaction technique, in a wide frequency range at different temperatures have been studied. All the samples exhibited β-type phase orthorhombic structure at room temperature. The Nyquist plot confirmed the presence of both grain and grain boundary effects for all Dy doped samples. Double relaxation behavior was also observed. The grain and grain boundary resistance decreases with rise in temperature for all the concentration and exhibits a typical negative temperature co-efficient of resistance (NTCR) behavior. An analysis of the electric modulus suggests the possible hopping mechanism for electrical transport processes of all the materials. The ac conductivity spectrum obeys Jonscher’s universal power law. DC conductivity of the materials were also studied and values of the activation energy found to be 0.40, 0.49, 0.73 and 0.78 eV for the compositions x = 0.05, 0.10, 0.15 and 0.20, respectively, at different temperatures (150–375 °C).

Introduction

Layered bismuth oxides of the general formula (Bi₂O₂)²⁺ (A _m − 1B _m O_3m + 1)²⁻ discovered by first Aurivillius [1]. Where A cations are generally K¹⁺, Ba²⁺, Sr²⁺, Ca²⁺, Bi³⁺, etc. while the B cations are Fe³⁺, Ti⁴⁺, Nb⁵⁺, W⁶⁺ and m ranges between 1 and 8 [2–4]. Crystal structures of these oxides consist of Bi₂O₂ layers interleaved with m-perovskite layers of the composition A _m − 1B _m O_3m + 1. When m = 1 and B = V⁵⁺, the formula can be written as Bi₄V₂O₁₁. The oxide Bi₄V₂O₁₁ with the Aurivillius layered perovskite structure was first reported by Venevtsev and later studied by Nowogrocki’s group [5, 6].

Abraham et al. [6] characterized the parent compound (Bi₄V₂O₁₁) by three essential polymorphs phase; α, β and γ. α (monoclinic and orthorhombic) phase exists at room temperature (RT) range and stable up to 440 °C; β (orthorhombic) phase is stable in the temperature range (440–560 °C) and γ (tetragonal) phase, which is fully oxygen disordered and found beyond 560 °C. The highly pure α-Bi₄V₂O_11 − δ phase has monoclinic structure. If the compound contains low level of impurities in the starting material, it stabilizes to a closely related orthorhombic form. The γ-polymorph phase is a good oxide-ion conductor at moderate temperatures because of the fully disordered oxygen vacancies in the perovskite vanadate layers. Solid solutions with high oxide anion conductivity derived from parent compound Bi₄V₂O₁₁ by partial substitution for vanadium site possesses good oxide anion conductivity at intermediate temperature. These materials are used for various applications such as catalysts, gas sensors, solid-state electrolytes, fuel cells and oxygen pumps. Sei-Ki Kim et al. studied the Co doped at the B site of Bi₄V_2 − x Co _x O_11 − δ and confirmed a high anisotropy of the ionic conductivity between the directions of both parallel and perpendicular to (Bi₂O₂)²⁺ layer [7]. Gupta et al. studied the Barium doped Bi₄Ba _x V_2 − x O_11 − δ (0.0 ≤ x ≤ 0.15) using melt quench technique [8]. Ravi Kant et al. also studied the Ti doped Bi₄V_2−x Ti _x O_11 − δ (0 ≤ x ≤ 0.4) [9]. Gupta et al. again studied Bi₄V_2 − x Mg _x O_11−δ (x = 0.05, 0.10 and 0.20) and Bi₄V_2 − x Ca _x O_11−δ (x = 0.05, 0.10, 0.15 and 0.20) [10]. Yasuda et al. studied the impedance analysis on electrical anisotropy of layer-structured Bi₄V_2(1 − x)Co_2x O_11 − δ single crystals [11]. Neelam Kumari et al. studied the dielectric, impedance and ferroelectric characteristics of C-oriented bismuth vanadate films grown by pulsed laser deposition [12]. Jugananda Sut et al. studied the A site doped lithium (Li) of Bi_4 − x Li _x V₂O_11 − δ (0 ≤ x ≤ 0.4) [13]. Al-Areqi et al. studied the double substitution (Co, Ni) of A-site doped BICO_0.20 − x NI _x VO _x (0 ≤ x ≤ 0.20) and found the maximum ionic conductivity at lower temperature (~2.56 × 10⁻⁴ S Cm⁻¹ at 300 °C) for concentration x = 0.13 [14]. Saba Beg et al. studied the structural and electrical properties of Bi₄Cr _x V_1 − x O_{5.5 + x − δ} (0 ≤ x ≤ 0.20) prepared by a micro wave-assisted route [15] and the effect of Cu–Al double substitution on the electrical properties of Bi₄V₂O₁₁ [16]. Gupta et al. studied that the composition Bi₄V_2 − x Sr _x O_11 − δ (0.05 ≤ x ≤ 0.20) prepared by melt quench technique and found that the grain size increases with dopant concentration which leads to increase the dielectric constant [17]. The present paper reports the synthesis, structural, electrical (impedance and modulus) and conductivity properties of layered bismuth oxide structure compounds of Dy doped Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) ceramics.

Experimental

Materials preparation

Solid-state reaction technique was used for the preparation of Dysprosium doped Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20). High purity ingredients; Bi₂O₃ (99%), Dy₂O₃ (99.9%), V₂O₅ (98.5%) were taken in a suitable stoichiometry to synthesize all samples. The compositions were mixed thoroughly using mortar and pestle, first in an air atmosphere for 1 h and then in methanol for 2 h so as to prepare good homogeneous fine powder. Then the fine powders were calcined in a high purity alumina crucible at an optimized temperature of 700 °C for 3 h in an air atmosphere. The formation of the compounds were checked by X-ray diffraction technique (XRD) at room temperature. Then the fine homogenous calcined powder were cold pressed into cylindrical pellets of 12 mm diameter and 1–2 mm of thickness at a pressure of 4 × 10⁶ N/m² using a hydraulic press. Polyvinyl alcohol (PVA) was used as binder in the fine powder which was burnt out during the high temperature sintering. Then the pellets were sintered at 750 °C for 3 h in an air atmosphere. Finally, the sintered pellets were polished with fine emery paper to make both the surfaces smooth and parallel. The pellets were coated with high purity silver paste and dried at temperature 150 °C for 1 h to remove moisture, if any, and then cooled to room temperature before carrying out the measurements of electrical properties.

Materials characterization

X-ray diffraction analysis of the calcined homogenous fine powders were studied at room temperature using a diffractometer (ULTIMA IV Model-Rigaku, Japan) using CuKα radiation (λ = 1.5405 Å) in a wide range of Bragg’s angle 2θ (20° ≤ θ ≤ 80°) with a scanning speed of 3°/min. The parameters such as electrical impedance (Z), phase angle (θ), loss tangent (tanδ) and capacitance (C _p) were measured using a computer-controlled impedance analyzer LCR meter (HIOKI Model: 3532) in laboratory-made sample holder and a heating arrangement in a wide frequency range (10²–10⁶ Hz) at different temperatures (25–450 °C) of the samples.

Results and discussion

Structural study

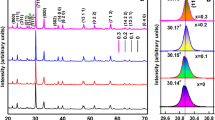
At room temperature, compared XRD pattern shown in Fig. 1 of fine homogenous calcined powders for all Dy compositions of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) were taken and confirmed an orthorhombic crystal structure. It is observed that, all the sample exhibit characteristic doublet at 2θ ≈ 32^o and singlet at 2θ ≈ 46^o, which suggests the β phase orthorhombic crystal structure at room temperature [16]. A good agreement between observed (obs) and calculated (cal) interplanar spacing d (∑Δd = d _obs − d _cal = minimum) was observed. The values of the lattice parameters shown in Table 1 were evaluated using a standard computer program package “POWD” [18] for all Dy concentration samples. The crystallite size (P) of Dy doped samples were roughly estimated from the broadening of a few XRD peaks (in a wide 2θ range) using the Scherrer’s equation [19], $P = K\lambda (\beta_{{\frac{1}{2}}} \cos \theta_{\text{hkl}} )$ (where K = constant = 0.89, λ = 1.5405 Å and β _1/2 = peak width of the reflection at half intensity). The average values of P were found to be 21–40 nm.

Fig. 1

XRD patterns of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at room temperature

Table 1 Values of lattice parameters of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20)

Impedance study

The complex impedance spectroscopy (CIS) [20] is the most important technique to study the electrical response (i.e., transport properties) of the material. Generally, the contribution of grain, grain boundary and electrode effect of a polycrystalline sample in a wide range of frequency at different temperatures can be analyzed. The electrical properties of the material is normally described in terms of complex dielectric constant (ε*), complex impedance (Z*), electric modulus (M*) and loss tangent (tanδ). These are related to each other as (1) $\varepsilon * = \varepsilon^{\prime} - j\varepsilon^{\prime\prime}$ (2) $Z* = Z^{\prime} - jZ^{\prime\prime}$ (3) $M* = \frac{1}{\varepsilon *(\omega )} = M^{\prime} + jM^{\prime\prime}$ (4) $\tan \delta = \frac{{\varepsilon^{\prime\prime}}}{{\varepsilon^{\prime}}} = \frac{{M^{\prime\prime}}}{{M^{\prime}}} = \frac{{Z^{\prime}}}{{Z^{\prime\prime}}}$, where (Z′, M′, ε′) and (Z′′, M′′, ε′′) are real and imaginary components of impedance, modulus and permittivity. A complex impedance spectrum of ceramic sample shows two distinct features intragrain (grain) and intergrain (grain boundary). Impedance data are presented in the form of Z′′ (capacitive) and Z′ (resistive). The complex impedance of the electrode/ceramic/electrode configuration can be explained as the sum of a single RC (R = resistance and C = capacitance) circuit in parallel combination.

Figures 2a–f and 3a–f shows the complex impedance spectrum (called as Nyquist plot) i.e., Z′ vs. Z′′ of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) over a wide range of frequency (100 Hz–1 MHz) at different temperatures (100–375 °C). Generally, the semicircle at higher and lower frequencies represents grain and electrode effect, respectively, while at intermediate frequencies it represents the grain boundary contribution. In these cases, two semicircles are observed in the Nyquist plot; first semicircle at low frequency represents the resistance of the grain boundary and second at high frequency represents the resistance of grain properties. It shows from the Figs. 2a–f and 3a–f that a single semicircular arc appears for all the concentration up to 125 °C. Above 125 °C, two semicircular arcs are formed, which shows the contribution of both grain (at the higher frequency side) and grain boundaries (at the lower frequency side) effect with their centers lying below the real axis. This confirms the existence of non-debye type relaxation. Similar type of behavior is also observed in other Bi-layered structured compound [21]. The above property of the material arises due to the double parallel combination of resistance and capacitance. From the complex impedance spectrum, the intercept point on the real axis shifts towards the origin with the increase in temperature. It indicates the decrease in the resistive property, i.e., grain and grain boundary of the materials like a semiconductor. The impedance data are well fitted with the ZSimpWin software with an equivalent circuit as shown in the Fig.  2a–f (inset) and Fig. 3a–f (inset) at temperatures 150, 200 and 350 °C for x = 0.05 − 0.20, where R, C, W and Q are resistance, capacitance, warburg and constant phase element (CPE). The values of fitting parameters of the circuits are shown in Table 2.

Fig. 2

a–f Complex impedance plot (Z′ vs. Z′′) with equivalent circuit (inset) of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05 and 0.10) at different temperatures

Fig. 3

a–f Complex impedance plot (Z′ vs. Z′′) with equivalent circuit (inset) of Bi₄V_2 − x Dy _x O₁₁ (x = 0.15 and 0.20) at different temperatures

Table 2 Values of fitting parameters of the equivalent circuits of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at 150, 200 and 350 °C

Figure 4a–d shows the variation of real part of the impedance (Z′) with frequency at different temperatures (250–325 °C) of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20). It is observed that at lower frequency range, the magnitude of Z′ (grain resistance) decreases with rise in temperature and appears to merge in the high frequency region. This may be due to the release of space charge polarization with rise in temperature and frequency [22]. On increasing the Dy concentration, the occurrence of space charge shifted to the higher frequency side. This may be due to the reduction in barrier properties of the materials with rise in temperature and responsible for the enhancement of conductivity. The space charge polarization occurs maximum at higher frequency side for x = 0.20 as compared to the other Dy compositions. This may be possible due to the Dy doped on vanadium sites of the samples. It is also observed that the value of same resistance for x = 0.15 and 0.20. Similar type of behavior is also observed in other studied material [17].

Fig. 4

a–d Variation of Z′ with frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures

Figure 5a–d shows the variation of imaginary part of the impedance (Z′′), generally called as loss spectrum, with frequency at different temperatures (250–325 °C) of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20). From Fig. 5a, b, it is observed that, at low frequency region, Z′′ initially decreases sharply with the increase in frequency and temperature but some peaks appear at intermediate frequency. These peaks are shifted towards higher frequency side in a decreasing manner, and finally, merge in the high frequency domain. From Fig. 5c, d, two peaks appeared in Z′′ at low and intermediate frequency region. Again these two peaks are shifted towards higher frequency side. The Z′′ peaks shifts to the lower frequencies with increasing Dy content, which indicates the presence of composition dependent electrical relaxation phenomenon in the system. This may by due to the immobile species at low temperatures and defect or vacancies at high temperatures [23]. The magnitude of Z′′ decreases with increase in frequency, as well as with temperature for all the Dy concentration. At higher frequency, it is clear that there is an absence of space charge effect in the materials. Similar type of behavior is also observed in other studied material [16].

Fig. 5

a–d Variation of Z′′ with frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures

Modulus study

The complex modulus spectroscopy is a very convenient tool to study the dynamical aspects of electrical transport phenomena in the materials. Generally, the complex electrical impedance spectrum gives more emphasis to elements with large resistance, whereas complex electric modulus spectrum plots highlight those with smaller capacitance. Using the complex modulus formula, the inhomogeneous nature of the polycrystalline materials with grain and grain boundary effects can be probed easily, which cannot be distinguished from complex impedance plot. The other advantage of the electric modulus spectrum formulae is the suppressed electrode effect. The real and imaginary components of the complex electric modulus (M*) were calculated using the relation M′ = $\omega C_{0} Z^{\prime\prime}$, $M^{\prime\prime} = \omega C_{0} Z^{\prime}(\omega = 2\pi f_{r} ,C_{0} = \frac{{\varepsilon_{0} A}}{t})$, where $\omega ,C_{0} ,\varepsilon_{0} ,A,t$ and $f_{r}$ are the angular frequency, geometrical capacitance, permittivity of free space, area of the electrode surface, thickness and relaxation frequency.

Figure 6a–d shows the variation of M′ as a function of frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures (250–325 °C). For all the samples, at lower frequency region, it shows a very low value (~zero) of M′. It shows a continuous increase in the dispersion with increase in frequency and then saturate at a maximum asymptotic value (i.e., M _∞ ) in the higher frequency region. This may be due to the presence of conduction phenomenon, short range mobility of charge carriers and also may possibly be related to a lack of restoring force for flow of charges under the influence of steady electrical field. The value of M′ decreases with rise in temperature in the high frequency region for all the Dy concentrations. Similar type of behavior also observed in other reported materials [24, 25].

Fig. 6

a–d Variation of M′ as a function of frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures

Figure 7a–d shows the variation of imaginary part of electric modulus (M′′) with frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures (250–325 °C). A well-defined relaxation mechanism are observed for the concentration x = 0.10–0.20 at different temperatures expect x = 0.05. The relaxation peaks shift towards higher frequency side with increase in temperature which correlates between the motions of mobile ions [26]. This suggests that the relaxation is thermally activated process. The asymmetry of peak broadening shows the spread of relaxation times with different time constant and hence the relaxation in the all compositions is of non-Debye type. The magnitude of the peak increases on increasing temperature. It is also observed that no peaks are obtained at 325 °C for all the Dy concentration of x = 0.05–0.20.

Fig. 7

a–d Variation of M′′ as a function of frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures

Figure 8a–d shows the complex modulus spectrum (M′ vs. M′′) of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at selected temperatures. The impedance data were again re-plotted in the modulus formula. A single semicircle is formed for all the Dy concentrations. It also confirms the presence of electrical relaxation phenomena in the materials. On increasing temperature, the intercept on real axis shifts towards the higher value of M′. It indicates the increase in capacitance of the all Dy concentration of the materials. The intercept point on the real axis indicates that the grain effect contribute the total capacitance. It also supports the negative temperature co-efficient of resistance type behavior of the materials since the grain capacitance (C _g) is inversely proportional to the grain resistance (R _g). Similar type of results also observed in other reported material [25, 27].

Fig. 8

a–d Complex modulus spectrum (M′ vs. M′′) of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures

Electrical conductivity study

Figure 9a–d shows the ac electrical conductivity as a function of frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures (250–325 °C). It is observed that the value of σ (ω) increases with increase in frequency, as well as temperature for all Dy concentration. It can be also be explained as frequency dependent conductivity of the materials by Jonscher’s universal power law [28] by the equation: $\sigma (\omega ) = \sigma_{\text{dc}} + A\omega^{n}$, where σ _dc is a dc conductivity at frequency independent in particular range of temperature, ‘A’ is the temperature dependent parameter and ‘n’ is the power law exponent, $A\omega^{n}$ consisting of the ac dependence and characterizes for all dispersion phenomena. It is confirmed to be a typical fit of the parameters A, n and σ _dc calculated by non-linear fit of the above equation with experimental data as shown in Table 3. The Navy blue solid lines are the fitted line for all the compositions. It is found that the value of the n vary between 0 and 1 (0 ≤ n ≤ 1) depending on temperature. This suggests that the electrical conduction in the materials are also due to thermally activated process [29, 30]. The ac conductivity is found to increase with increase in both frequency as well as Dy concentration. The conductivity pattern is a strongly dependent frequency and obeys a power relation σ _ac α ω ⁿ for all temperature. It clearly indicates that the low and high frequency dispersive regions are separated by a change in slope at a particular frequency at temperature 325 °C for all concentration. There is an appearance of plateau region in the low frequency side and shows a change in slope at a particular frequency known as hopping frequency.

Fig. 9

a–d Variation of ac conductivity with frequency of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20) at different temperatures

Table 3 Value of fitting parameters obtained from Jonscher’s power law at different temperatures

The electrical conductivity (σ _dc ) is thermally activated process and which obeys the Arrhenius law; $\sigma_{dc} = \sigma_{0} \exp \left( {\frac{{ - E_{a} }}{{K_{\text{B}} T}}} \right),$ where the symbols having their usual meaning. Figure 10 shows the variation of σ _dc (grain) with inverse of absolute temperature (10³/T) of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20). The dc conductivity of the material were evaluated using the relation $\sigma = \frac{l}{{R_{\text{g}} A}}$, where l is the thickness, R _g is the grain resistance (calculated from Nyquist plot) and A is the area of cross-section of the samples. A linear fit of σ _dc vs. (10³/T) plot has been used to calculate from the slope of straight line. The values of activation energy (E _a) are found to be 0.40, 0.49, 0.73 and 0.78 eV for x = 0.05, 0.10, 0.15 and 0.20, respectively, in the temperature range 150–375 °C. The dc conductivity increases with increase in Dy concentration for all the samples. From the plot, it is clear that the grain resistance decreases with rise in temperature and indicates negative temperature co-efficient of resistance like a semiconductor.

Fig. 10

Variation of dc conductivity with inverse of temperature of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05, 0.10, 0.15 and 0.20)

Conclusions

The polycrystalline samples of Bi₄V_2 − x Dy _x O₁₁ (x = 0.05–0.20) were prepared by the solid-state reaction technique has been studied. The phase formation is confirmed by X-ray analysis which exhibits β phase orthorhombic crystal structure for all Dy concentration at room temperature. The complex impedance plots exhibit both grain and grain boundary effect. Both grain (R _g) and grain boundary (R _gb) decreases with rise in temperature indicating the negative temperature co-efficient of resistance (NTCR) behavior for all the samples. All the samples show frequency dependence of ac conductivity which obeys the universal power law. Modulus analysis has been carried out to understand the mechanism of electrical transport process and also indicates non-Debye type conductivity relaxation for all Dy doped samples.