Introduction

Developing new concepts to improve the efficiency of photovoltaic solar cells is a well-known challenge for the scientific community. In 1961 Shockley and Queisser [1] brought out the theoretical limit of a photovoltaic solar cell. The results of their study are worldwide recognized as theoretical limit of efficiency for a single pn-junction solar cell. After them, many studies have been carried out to explore the possibilities of exceeding this limit. Different technologies and methods were used for that purpose [2–15]. Among these approaches, we could cite tandem cells, concentrator cell, carrier multiplication, down conversion, hot carriers, etc.

In 1997, by considering the impact ionization phenomenon to generate hot electrons, Würfel [11] found a maximum efficiency of 85% for a vanishing band gap of the solar cell. In 1993, Landsberg et al. [12] reported an efficiency of 60.3% at E G = 0.8 eV for a solar cell submitted to band–band impact ionization effect. By considering the impact ionization effects on the efficiency of intermediate band solar cells, Gorji [16] has obtained a thermodynamic efficiency of 81.2%, which was higher than the maximum efficiency of 63.2% for an intermediate band without impact ionization mechanism. All these results show that the impact ionization phenomenon is very promising for the improvement of solar cell efficiency.

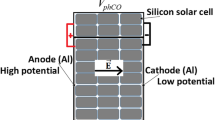
Impact ionization is a process in which a charge carrier with high kinetic energy collides with a second charge carrier transferring its kinetic energy to the latter which is hereby lifted to higher energy level [17]. This process increases the number of charge carriers. There are many impact ionization models. One can have: the one carrier model and the two carrier models which are often classified as band–band and band-trap impact ionization [18]. The current study focuses on the band trap impact ionization of the solar cell to reach a high efficiency. Free carriers are subject to trapping [19]. The default and the presence of some impurities in the solar cell material introduce trap levels into the band gap. These levels can emit an electron towards conduction band (case A in Fig. 1), receive an electron from valence band (case B in Fig. 1), receive an electron from conduction band (case C in Fig. 1) or loss an electron towards valence band (case D in Fig. 1). The cases A and B are those on which this paper focused because they permit to generate additional free charge carriers. These cases can easily been obtained through the process of impact ionization induced by an external source of energy. The current study considers an external applied electric field as the parameter which induces the impact ionization. The models of generation–recombination mechanism with band trap impact ionization involving electrons and holes are presented in Refs. [18, 20–23].

Fig. 1
figure 1

Transition of charge carriers via trap level

Full size image

A single pn-junction of the solar cell is considered in this work. In Ref. [17] it has been shown that outside an electron diffusion length L n to the right or a hole diffusion length L p to the left of the pn-junction, the charge current through a pn-junction is a pure electron current in the n-region and a pure hole current in the p-region. This charge current is then given by integrating over the contributions to the electron current (alternatively, the contributions to the hole current). Knowing the number of free electrons in n-region (or free holes in p-region) could be sufficient to evaluate the charge current through a pn-junction and thus the open circuit voltage. In this paper, the number of free electrons in n-region of the pn-junction is evaluated by solving the reaction diffusion equation. This equation is solved with the factorization method. The total hole-electron generation rate due to the solar radiation is evaluated by following the Shockley–Queisser approach [1].

Studied model

The current delivered by a photovoltaic solar cell is based on the generation–recombination mechanism. The generation–recombination model in this paper is based on the band trap impact ionization phenomenon involving two carriers (holes and electrons). The rate equations of the model are:

$$f_{n} \left( {n,p} \right) = Y + \left[ {X_{1} N_{D}^{*} - X_{1} n - \left( {B - X_{1} } \right)p} \right]n$$
(1a)
$$f_{p} \left( {n,p} \right) = Y + \left[ {X_{2} P_{D} - X_{2} p - \left( {B - X_{2} } \right)n} \right]p$$
(1b)

where n and p are the number of free electrons and free holes, respectively. The variables X 1 and X 2 are band-trap impact ionization coefficients (to generate additional electrons and holes, respectively) which depend on the applied electric field. Y and B are the band–band generation coefficient and the band–band recombination coefficient, respectively. Y is a photo-generation parameter due to the illumination of solar cell. This variable is evaluated through Eq. (43). The constants N * D and N t are the effective donor density and the trap density, respectively. P D  = N t − N * D .

Considering the fact that the total charge current through a pn-junction is a pure electron current in the n-region, the knowledge of the free electrons number in the n-region is requested to determine the total charge current through the pn-junction. Considering only the transverse direction and neglecting the transverse electric field, the number of free electrons can be determined using the reaction–diffusion equation presented in Eq. (2).

$$\frac{{{\partial }n}}{\partial t} - D_{n} \frac{{\partial^{2} n}}{{\partial x^{2} }} = f_{n} (n,p)$$
(2)

In steady state regime, \(\frac{\partial n}{\partial t} = 0\). Thus Eq. (2) turns to:

$$\frac{{\partial^{2} n}}{{\partial x^{2} }} + \frac{{f_{n} (n,p)}}{{D_{n} }} = 0$$
(3)

the constant D n is the electron diffusion coefficient defined by:

$$D_{n} = \mu_{n} \frac{{kT_{\text{c}} }}{q}$$
(4)

Thermodynamic efficiency calculation

Resolution of the reaction–diffusion equation

The factorization method [24, 25] is used in this work to solve the reaction–diffusion equation. The equation to solve is Eq. (3).

By setting \(D = \frac{\partial }{\partial x}, D^{2} = \frac{{\partial^{2} }}{{\partial x^{2} }}, g_{1} \left( {n,p} \right) = 0,\;{\text{and}}\;f_{1} \left( {n,p} \right) = \frac{{f_{n} (n,p)}}{{D_{n} }},\)The Eq. (3) can turn to:

$$\left( {D^{2} + g_{1} \left( {n,p} \right)D + \frac{{f_{1} (n,p)}}{n}} \right)n = 0$$
(5)

The Eq. (5) can be factorized as:

$$\left( {D - \psi_{12} } \right)\left( {D - \psi_{11} } \right)n = 0$$
(6)

where

$$f_{1} \left( {n,p} \right) = n \psi_{12} \psi_{11}$$
(7)

The Eq. (3) can be developed and leads to:

$$n^{\prime\prime} - \left( {\psi_{11} + \psi_{12} + n\frac{{\partial \psi_{11} }}{\partial n}} \right)n^{\prime} + \psi_{12} \psi_{11} n = 0$$
(8)

The comparison of Eqs. (3) and (8) leads to:

$$0 = - \left( {n\frac{{\partial \psi_{11} }}{\partial n} + \psi_{11} + \psi_{12} } \right)$$
(9)
$$\frac{{f_{n} (n,p)}}{{D_{n} }} = \psi_{12} \psi_{11} n$$
(10)

Eq. (1a) leads to:

$$\frac{{f_{n} (n,p)}}{{D_{n} }} = \frac{1}{{K_{1} D_{n} }}\left( {1 - \frac{{\left( {B - X_{1} } \right)p}}{{\frac{Y}{n} + X_{1} \left( {N_{D}^{*} - n} \right)}}} \right) \times K_{1} \left( {\frac{Y}{n} + X_{1} \left( {N_{D}^{*} - n} \right)} \right)n$$
(11)

Therefore, referring to Eq. (10), \(\psi_{ij}\) could be choosing such as:

$$\psi_{11} = K_{1} \left( {\frac{Y}{n} + X_{1} \left( {N_{D}^{*} - n} \right)} \right)$$
(12a)
$$\psi_{12} = \frac{1}{{K_{1} D_{n} }}\left( {1 - \frac{{\left( {B - X_{1} } \right)p}}{{\frac{Y}{n} + X_{1} \left( {N_{D}^{*} - n} \right)}}} \right)$$
(12b)

where K 1 is an arbitrary constant to be determined.To determine the constants K 1 let us consider Eq. (9). This equation can be developed and leads to,

$$K_{1}^{2} X_{1} N_{D}^{*} + \frac{1}{{D_{n} }} - 2K_{1}^{2} X_{1} n - \frac{{\left( {B - X_{1} } \right)p}}{{D_{n} \left( {\frac{Y}{n} + X_{1} N_{D}^{*} - X_{1} n} \right)}} = 0$$
(13)

The Eq. (13) admits solution if:

$$\left\{ {\begin{array}{*{20}l} {K_{1}^{2} X_{1} N_{D}^{*} + \frac{1}{{D_{n} }} = 0,} \\ {\text{or}} \\ { - 2K_{1}^{2} X_{1} n - \frac{{\left( {B - X_{1} } \right)p}}{{D_{n} \left( {\frac{Y}{n} + X_{1} N_{D}^{*} - X_{1} n} \right)}} = 0} \\ \end{array} } \right.$$
(14)

The first condition of Eq. (14) leads to:

$$K_{1} = i\sqrt {\frac{1}{{X_{1} N_{D}^{*} D_{n} }}} ,$$
(15)

The Eq. (5) transformed to two possible differential equations of first order such as [25]:

$$n^{\prime} - \psi_{11} \left( {n,p} \right)n = 0$$
(16a)
$$n^{\prime} - \psi_{12} \left( {n,p} \right)n = 0$$
(16b)

Let us consider Eq. (16a). The replacement of Eq. (12a) into Eq. (16a) leads to:

$$\mathop \int \nolimits \frac{{{\text{d}}n}}{{Y + X_{1} \left( {N_{D}^{*} - n} \right)n}} = \mathop \int \limits_{{z_{0} }}^{z} K_{1} {\text{d}}z$$
(17)

The Eq. (17) permits to obtain:

$$\left| {\frac{n - \alpha }{n - \beta }} \right| = e^{{K_{1} \sqrt \Delta \left( {z - z_{0} } \right)}}$$
(18)

where

$$\Delta = \left( {X_{1} N_{D}^{*} } \right)^{2} +\; 4YX_{1} ,$$
(19a)
$$\alpha = \frac{{X_{1} N_{D}^{*} - \sqrt \Delta }}{{2X_{1} }},$$
(19b)

and

$$\beta = \frac{{X_{1} N_{D}^{*} + \sqrt \Delta }}{{2X_{1} }}$$
(19c)

We have to consider two cases:

First case

For \(\left| {\frac{n - \alpha }{n - \beta }} \right| = - \frac{n - \alpha }{n - \beta }\), Eq. (18) leads to:

$$n = \frac{\alpha }{{1 + e^{{K_{1} \sqrt \Delta \left( {x - x_{0} } \right)}} }} + \frac{{\beta e^{{K_{1} \sqrt \Delta \left( {x - x_{0} } \right)}} }}{{1 + e^{{K_{1} \sqrt \Delta \left( {x - x_{0} } \right)}} }}$$
(20)

By setting \(K_{1} = iK_{2}\), Eq. (20) can turn to:

$$n = \frac{{\alpha e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }} + \frac{{\beta e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \Delta \left( {x - x_{0} } \right)/2}} }}$$
(21)

where

$$K_{2} = \sqrt {\frac{1}{{X_{1} N_{D}^{*} D_{n} }}}$$
(22)

By setting \(\gamma = \frac{{\alpha e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }} \;{\text{and}}\;\delta = \frac{{\beta e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }},\) one could have:

$$\gamma = \frac{{\alpha \left( {\frac{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{2}} \right) + \alpha e^{{ - iK_{2} \sqrt \Delta \left( {z - z_{0} } \right)/2}} - \alpha \left( {\frac{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{2}} \right)}}{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}$$
(23a)

and

$$\delta = \frac{{\beta \left( {\frac{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{2}} \right) + \beta e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} - \beta \left( {\frac{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}{2}} \right)}}{{e^{{iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} + e^{{ - iK_{2} \sqrt \Delta \left( {x - x_{0} } \right)/2}} }}$$
(23b)

Equations (23a) and (23b) turn to:

$$\gamma = \frac{\alpha }{2}\left( {1 - { \tan }\left( {\frac{{K_{2} \sqrt \Delta \left( {x - x_{0} } \right)}}{2}} \right)} \right)$$
(24a)

and

$$\delta = \frac{\beta }{2}\left( {1 + { \tan }\left( {\frac{{K_{2} \sqrt \Delta \left( {x - x_{0} } \right)}}{2}} \right)} \right)$$
(24b)

Thus, Eq. (20) turns to:

$$n = \frac{\alpha }{2}\left( {1 - { \tan }\left( {\frac{{K_{2} \sqrt \Delta \left( {x - x_{0} } \right)}}{2}} \right)} \right) + \frac{\beta }{2}\left( {1 + { \tan }\left( {\frac{{K_{2} \sqrt \Delta \left( {x - x_{0} } \right)}}{2}} \right)} \right)$$
(25)

By replacing α and β by their expressions in Eq. (25) one obtains:

$$n = \frac{{N_{D}^{*} }}{2} - \frac{\sqrt \Delta }{{2{\text{X}}_{1} }}{ \tan }\left( {\frac{{K_{2} \sqrt \Delta \left( {x - x_{0} } \right)}}{2}} \right)$$
(26)

Second case

For \(\left| {\frac{n - \alpha }{n - \beta }} \right| = \frac{n - \alpha }{n - \beta }\), Eq. (18) leads to:

$$n = \frac{\alpha }{{1 - e^{{K_{1} \sqrt \Delta \left( {x - x_{0} } \right)}} }} - \frac{{\beta e^{{K_{1} \sqrt \Delta \left( {x - x_{0} } \right)}} }}{{1 - e^{{K_{1} \sqrt \Delta \left( {x - x_{0} } \right)}} }}$$
(27)

Following a same approach like in the first case, one gets:

$$n = \frac{{N_{D}^{*} }}{2} + \frac{\sqrt \Delta }{{2X_{1} }}{ \cot }\left( {\frac{{K_{2} \sqrt \Delta \left( {x - x_{0} } \right)}}{2}} \right)$$
(28)

Charge current density through the pn-junction

According to Ref. [17], the total charge current through a pn-junction could be expressed by:

$$j_{\text{Q}} = q\mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} \text{div}j_{n} {\text{d}}x$$
(29)

where

$$L_{n} = \sqrt {D_{n} \tau_{n} }$$
(30a)
$$L_{p} = \sqrt {D_{p} \tau_{p} }$$
(30b)
$$D_{p} = \mu_{p} \frac{{kT_{\text{c}} }}{q}$$
(30c)

From the continuity equation for electrons, one gets:

$${\text{div}}j_{n} = q\left( {\frac{\partial n}{\partial t} - f_{n} (n,p)} \right)$$
(31)

By replacing Eq. (1a) into Eq. (31) and Eq. (31) into Eq. (29), and considering the fact that \(\frac{\partial n}{\partial t} = 0\) (steady state condition), then Eq. (29) turns to:

$$j_{\text{Q}} = - q^{2} \mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} Y{\text{d}}x - q^{2} X_{1} N_{D}^{*} \mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} n{\text{d}}x + q^{2} X_{1} \mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} n^{2} {\text{d}}x + q^{2} \left( {B - X_{1} } \right)\mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} pn{\text{d}}x$$
(32)

For simplicity let us set:

$$\theta_{1} = q^{2} \mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} Y{\text{d}}x,$$
(33a)
$$\theta_{2} = q^{2} X_{1} N_{D}^{*} \mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} n{\text{d}}x,$$
(33b)
$$\theta_{3} = q^{2} X_{1} \mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} n^{2} {\text{d}}x,$$
(33c)
$$\theta_{4} = q^{2} \left( {B - X_{1} } \right)\mathop \int \limits_{{ - L_{p} }}^{{L_{n} }} pn{\text{d}}x$$
(33d)

The calculation of θ 1 , θ 2 , θ 3 and θ 4 leads to:

$$\theta_{1} = q^{2} Y\left( {L_{n} + L_{p} } \right)$$
(34a)
$$\theta_{2} = q^{2} X_{1} N_{D}^{*} \left( {\frac{{N_{D}^{*} }}{2}\left( {L_{n} + L_{p} } \right) + \frac{1}{{K_{2} X_{1} }}\log \left| {\cos \left( {\frac{{K_{2} \sqrt \Delta }}{2}\left( {L_{n} - x_{0} } \right)} \right)} \right| - \frac{1}{{K_{2} X_{1} }}\log \left| {\cos \left( {\frac{{K_{2} \sqrt \Delta }}{2}\left( { - L_{p} - x_{0} } \right)} \right)} \right|} \right)$$
(34b)
$$\theta_{3} = q^{2} X_{1} \left( \begin{aligned} \left( {\frac{{N_{D}^{*2} }}{4} - \frac{\Delta }{{4X_{1}^{2} }}} \right)\left( {L_{n} + L_{p} } \right) + \frac{{N_{D}^{*} }}{{K_{2} X_{1} }}\log \left| {\cos \left( {\frac{{K_{2} \sqrt \Delta }}{2}\left( {L_{n} - x_{0} } \right)} \right)} \right| - \frac{{N_{D}^{*} }}{{K_{2} X_{1} }}\log \left| {\cos \left( {\frac{{K_{2} \sqrt \Delta }}{2}\left( { - L_{p} - x_{0} } \right)} \right)} \right| \hfill \\ + \frac{\sqrt \Delta }{{2K_{2} X_{1}^{2} }}\tan \left( {\frac{{K_{2} \sqrt \Delta }}{2}\left( {L_{n} - x_{0} } \right)} \right) - \frac{\sqrt \Delta }{{2K_{2} X_{1}^{2} }}\tan \left( {\frac{{K_{2} \sqrt \Delta }}{2}\left( { - L_{p} - x_{0} } \right)} \right) \hfill \\ \end{aligned} \right)$$
(34c)
$$\theta_{4} = q^{2} n_{\text{i}}^{2} \left( {B - X_{1} } \right)\left( {L_{n} + L_{p} } \right){ \exp }\left( {\frac{qV}{{kT_{\text{c}} }}} \right)$$
(34d)

Thus, Eq. (32) could be rewritten as:

$$j_{\text{Q}} = - \theta_{1} - \theta_{2} + \theta_{3} + q^{2} n_{\text{i}}^{2} \left( {B - X_{1} } \right)\left( {L_{n} + L_{p} } \right){ \exp }\left( {\frac{qV}{{kT_{\text{c}} }}} \right)$$
(35)

The short-circuit current j sc (when V = 0) is defined as:

$$j_{\text{sc}} = - \theta_{1} - \theta_{2} + \theta_{3} + q^{2} n_{\text{i}}^{2} \left( {B - X_{1} } \right)\left( {L_{n} + L_{p} } \right)$$
(36)

Equation (35) could be rewritten as:

$$j_{\text{Q}} = j_{\text{sc}} + q^{2} n_{\text{i}}^{2} \left( {B - X_{1} } \right)\left( {L_{n} + L_{p} } \right)\left( {{ \exp }\left( {\frac{qV}{{kT_{\text{c}} }}} \right) - 1} \right)$$
(37)

By considering the dark where j sc = 0 and for large negative voltages (where \({ \exp }\left( {\frac{qV}{{kT_{\text{c}} }}} \right) \ll 1\)), one gets the reverse saturation current j s as:

$$j_{\text{s}} = q^{2} n_{\text{i}}^{2} \left( {B - X_{1} } \right)\left( {L_{n} + L_{p} } \right)$$
(38)

From the relation

$$j_{\text{Q}} = j_{\text{sc}} + j_{\text{s}} \left( {{ \exp }\left( {\frac{qV}{{kT_{\text{c}} }}} \right) - 1} \right) ,$$
(39)

the open circuit voltage (when j Q = 0) is deducted as:

$$V_{\text{oc}} = \frac{{kT_{\text{c}} }}{q}\ln \left( {1 - \frac{{j_{\text{sc}} }}{{j_{\text{s}} }}} \right)$$
(40)

According to Ref. [17], the thermodynamic efficiency is given by:

$$\eta_{\text{thermodynamic}} = \frac{{qV_{\text{oc}} }}{{E_{\text{G}} + 3kT_{\text{c}} }}$$
(41)

According to Ref. [1], the photo-generation rate of hole-electron pairs Y is defined by:

$$Y = Sf_{\omega } t_{\text{s}} Q_{\text{s}}$$
(42)

where

$$Q_{\text{s}} = \left[ {2\pi \left( {kT_{\text{s}} } \right)^{3} /\left( {h^{3} c^{2} } \right)} \right]\mathop \smallint \limits_{{x_{\text{g}} }}^{\infty } \frac{{x^{2} {\text{d}}x}}{{e^{x} - 1}}$$
(43)
$$x_{\text{g}} = \frac{{E_{\text{G}} }}{{kT_{\text{s}} }}$$
(44)

.

Discussion

All the needed parameters for simulation are presented in Table 1.

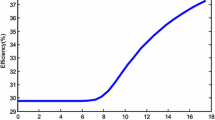
Table 1 Typical materials parameters corresponding to α-si near room temperature for the g–r process of band-trap impact ionization [18]
Full size table

Figure 2 presents the thermodynamic efficiency of the studied silicon solar cell modeled as an increase function for the external applied electric field in the range of 0–1586 V/Cm. An efficiency of 67% is reached for E o = 1586 V/Cm. From E o > 1586 V/Cm an efficiency fluctuation (increasing and decreasing) is noted. This fluctuation could be due to current instabilities which emerge from solar cells (which are semiconductors) when the applied electric field is increasing [26]. Figure 3 has been plotted for 0 < E o < 106 V/Cm and shows that the solar cell could reach a high efficiency for strong electric field as it is the case for E o = 8 × 105 V/Cm where an efficiency of 72.7% has been reached. In this case, the problem is that, for the same value of electric field, there are different values of efficiency because of fluctuations. Therefore, it could be difficult to determinate exactly the high efficiency of the solar cell subjected to impact ionization (induced by an external applied electric field) in the margin of which efficiency fluctuates and is unstable. The results obtained shows that the band-trap impact ionization of charge carriers induced by an applied electric field could be an interesting solution to reach a high efficiency of the photovoltaic solar cells. However, it is very important to know and avoid applying electric field belonging to the range which induces efficiency instabilities. Theoretically a high efficiency of solar cell could be reached even for applied electric fields of average intensity (67% has been reached at E o = 1586 V/Cm).

Fig. 2
figure 2

Thermodynamic efficiency versus external applied electric field for 0 < Eo < 104 V/Cm. T c = 300 K, T s = 6000 K, S = 1 Cm², f ω  = 2.18 × 10−5, t s = 1, τ n  = τ p  = 10−6 s, x 0 = 0

Full size image
Fig. 3
figure 3

Thermodynamic efficiency versus external applied electric field for 0 < Eo < 106 V/Cm. T c = 300 K, T s = 6000 K, S = 1 Cm², f ω  = 2.18 × 10−5, t s = 1, τ n  = τ p  = 10−6 s, x 0 = 0

Full size image

Conclusion

In this paper, the effect of an external applied electric field on the thermodynamic efficiency of a silicon photovoltaic solar cell has been studied. Theoretically, it has been shown that an auxiliary applied electric field could be a very promising solution to reach a high efficiency of the solar cells. However, it is not always the stronger electric field which is necessary to induce the higher efficiency. There are efficiency instabilities for strong applied electric field to solar cells.