Abstract
In this paper, a new numerical technique implements on the time-space pseudospectral method to approximate the numerical solutions of nonlinear time- and space-fractional coupled Burgers’ equation. This technique is based on orthogonal Chebyshev polynomial function and discretizes using Chebyshev–Gauss–Lobbato (CGL) points. Caputo–Riemann–Liouville fractional derivative formula is used to illustrate the fractional derivatives matrix at CGL points. Using the derivatives matrices, the given problem is reduced to a system of nonlinear algebraic equations. These equations can be solved using Newton–Raphson method. Two model examples of time- and space-fractional coupled Burgers’ equation are tested for a set of fractional space and time derivative order. The figures and tables show the significant features, effectiveness, and good accuracy of the proposed method.
Similar content being viewed by others
1 Introduction
The time- and space-fractional Burgers’ equations arise in areas of many phenomena such as material science, hereditary effects on nonlinear acoustic waves, chemical reaction fluid mechanics, plasma physics, optical fibers, and finance [5, 17, 26, 32].
In this paper, let us consider time-fractional-coupled Burgers’ equation:
and space-fractional-coupled Burgers’ equation:
with initial condition:
and boundary conditions:
where \(\Omega ^{}= \left[ x_{L},x_{R}\right] ^{} \), \( \alpha _{1} \) and \( \beta _{1} \) are order of time-fractional derivative, and \( \alpha _{2} \) and \( \beta _{2} \) are order of space-fractional derivative.
In past years, several analytical and numerical methods have been developed for the time- and space-fractional coupled Burger’s equation. Kurt et al. [16] have proposed exp- function method and perturbation–iteration method for the analytical solutions of nonlinear time-fractional coupled Burgers’ equations. Senol et al. [27] have introduced residual power series method for the numerical solutions of time-fractional burgers’ type equation with conformable fractional derivative. Cenesiz et al. [7] have obtained new type exact solutions for time-fractional Burgers’ equation, modified Burgers’ equation, and Burgers’–Korteweg–de-Vries equation using first integral method. Islam et al. [15] have obtained extract exact solutions for space-time-fractional Burgers’ equation using rational fractional expansion method. Furthermore, authors have also employed exp-function method and the extended tanh method to construct the closed form solutions. Prakash et al. [25] have proposed fractional variational iteration method for the numerical solutions of time- and space-fractional coupled Burgers’ equations. Chen and Li An [8] have introduced the Adomian decomposition method for numerical solutions of coupled Burgers’ equations with time- and space-fractional derivatives. Yildirim and Kelleci [30] have proposed homotopy perturbation method for the numerical solutions of coupled Burgers’ equations with time- and space-fractional derivatives. Asgari and Hosseini [3] have proposed two semi-implicit Fourier spectral schemes for the numerical solution of generalized time-fractional Burger’s equation. In this method, the authors have shown unconditional stability and improve the computational cost. Momani [24] has obtained the non-perturbative analytical solutions of space- and time-fractional Burgers’ equations using Adomian decomposition method and describe the physical processes of unidirectional propagation of weakly nonlinear acoustic waves through a gas-filled pipe. Mohammadizadeh et al. [23] have obtained unique solutions under some special conditions for a special class of fractional Burgers’ equation. They have also found at least one optimal solution for this problem. Moreover, this equation was solved by many different numerical methods such as finite-difference method [18, 19], finite-element method [31, 33], variational iteration method [14], spectral method [4, 20,21,22], Adomian decomposition method [1], b-spline method [9, 11, 12], Galerkin method [6], homotopy algorithm [29], generalized exp-function method [10], finite volume method [13], residual power series method [34], and homotopy perturbation method [2], etc.
This paper is organized as follows. In Sect. 2, we describe some basic definitions and notations. Discretizing and description of the methods are presented in Sects. 3 and 4. In Sect. 5, we present the convergence analysis of time- and space-fractional coupled Burgers’ equation. In Sect. 5, we present numerical solutions and errors by the proposed scheme. Finally, the conclusion of our work is given in the last section.
2 Preliminary
In this section, the definition of the Caputo–Riemann–Liouville fractional derivative is introduced systematically.
Definition 2.1: The partial fractional derivatives of order \( n-1<\nu <n \) of a function \( \L _{M}(t) \), with respect to variable t, in the Caputo–Riemann–Liouville fractional derivative formula are defined by:
where \( \nu \ge 0 \) is the order of derivative, \( \Gamma \) is the gamma function, and \( n=\lceil \nu \rceil +1 \) with \( \lceil \nu \rceil \) denoting the integral part of \( \nu \). Caputo–Riemann–Liouville fractional derivatives have some basic properties which are needed in this paper as follows:
Moreover, construction of the first-order Chebyshev fractional differential matrix is given as:
3 Pseudospectral methodology
The method allows the representation of functions and their derivatives at given set of grid points and approximate solutions of nonlinear partial differential equations as a sum of basis functions in both space and time directions.
We seek a pseudospectral approximation F(x, t), as a finite linear combination of a chosen set of orthogonal basis functions for the one-dimensional form:
where the trial basis functions defined by:
and
Here, z is a dummy variable and represents x in spatial and t in time direction, \(\tau _i(x)\) and \(\tau _j(t)\) are \(M^{th}\) degree Lagrange polynomials in spatial and time variables, and \( F(x_{i},t_{j}) \) are unknowns spectral coefficients. Let us define Chebyshev–Gauss–Lobatto points (CGL points):
These points are projection of equispaced points on upper half of unit circle on \( [ -1, 1] \) and make cluster at boundaries.
Next, define the Chebyshev differentiation matrix at CGL points \(\left\{ z_{0}, z_{1},\ldots ,z_{M} \right\} \), which is used to approximate the derivatives of F(x, t) in the spatial and time directions. The first derivative matrix \(D^{(1)}\) is defined by:
Then, Eq. (3.1) can be expressed in the form of direct product as:
where
In this manner, first spatial derivative of the function can be defined as follows:
In similar fashion, first spatial fractional derivative of the function can be defined as follows:
Next, time derivative and time-fractional derivative of the function can be defined by:
Similarly, the second spatial derivative of the function is given by:
where \( D^{(2)}= D^{(1)}\times D^{(1)}\).
4 Pseudospectral method-based discretization
Furthermore, let us consider following transformations which are used to transform the one-dimensional space \( [x_{L},x_{R}] \), \( [y_{L},y_{R}] \) and time [0, T] in to \( [-1,1] \). We obtain the time fractional coupled Burgers’ equation in new space and time interval:
and space-fractional coupled Burgers’ equation:
with initial conditions:
and boundary conditions:
Furthermore, we consider a mapping for converting the non-homogeneous initial and boundary values to homogeneous initial and boundary values:
Define new variables \(Y_{k}(x,t),~\forall k=\left\{ 1,2\right\} \):
the above time-fractional coupled Burgers’ equation can be modified with new variables and obtained the residuals:
and obtain the residuals of space-fractional coupled Burgers’ equation:
Now, we apply CGL points and pseudospectral method in coupled equations and obtained the system of nonlinear algebraic equation:
The system of nonlinear equation (4.6) can be solved using Newton–Raphson method.
5 Convergence analysis
In this section, author study for the error analysis of the suggested expansion of Chebyshev polynomials is investigated.
Theorem 51
If the series \( \sum _{i=0}^{\infty } \sum _{k=0}^{\infty }{\tau _{i}(x) \tau _{k}(t) \varTheta _{ik}} \) converges uniformly to \( Z_{1}(x,t) \) on the interval \( [-1,1]^{2} \), then we have:
Proof
We know that:
Taking \( L_{w^{}}^{2}[- 1,1] \) norm both side, we get:
Finally, put the value of discrete inner product, and we get:
Hence, function \( Z_{1}(x,t) \) is bounded. In a similar fashion, we can obtain function \( Z_{2}(x,t) \) is bounded. \(\square \)
6 Numerical results and discussion
In this section, to demonstrate the performance, the proposed method is implemented on test problems of time- and space-fractional Burgers’ equation. Error at different grid points will be expressed in terms of \( L_{2} \)- norm which is defined by:
where \(Z_{i}^\mathrm{exa}\) and \(Z_{i(\alpha ,\beta )}^\mathrm{num},~~~ \forall i\in {1,2},\) represent exact solutions and numerical solutions, respectively.
6.1 Example 1
Let us consider the time-fractional coupled Burgers’ equation:
with initial condition:
the exact solution for the problem is given: [1]
When \( \alpha _{1}=\beta _{1}=1 \), then exact solution is:
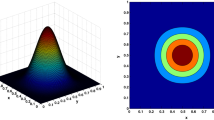
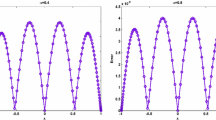
In this example, numerical solutions of the proposed method have obtained over the domain \( \Omega =[- 10,10]^{},~~ t \in [0,0.005] \) and fractional-order derivative \( 0< \alpha _{1},\beta _{1} \le 1 \). The error norms for different grid points and different fractional-order derivatives are presented in Table 1. In Table 1, it can be seen that the accuracy of the numerical results is increased along with the number of grid points. We are also depicted the 3D graph of numerical solutions \( Z_{1} \) and \( Z_{2} \) at time \( T= 0.005 \) and \( \alpha _{1}=0.5,\beta _{1}=0.25 \) in Fig. 1. Figure 2 illustrates the 2D curve of the numerical and exact solutions with different fractional-order derivatives at time \( T=0.005 \). In this figure, the solid line represents the exact solutions; however, the block represents the numerical solutions at various \( \alpha _{1} \) and \( \beta _{1} \). Accuracy of numerical solutions is merely seen in Fig. 2. Authors have discussed the numerical solutions of the equation with the different set of data, and for comparison purpose, we refer to [1, 8, 28, 30]. Furthermore, it is found that the results obtained by the proposed method show very good agreement with published results. Moreover, proposed method has obtained the eighth order of accuracy.
6.2 Example 2
Let us consider the space-fractional coupled Burgers’ equation:
with initial condition:
the exact solution for the problem is given as: [8, 30]
where
In this example, numerical solutions of the proposed method have obtained over the domain \( \Omega =[0,10]^{},~~ t \in [0,1] \) and fractional-order derivative \( 0< \alpha _{2},\beta _{2} \le 1 \). The error norms for different grid points and different fractional order derivatives are presented in Table 2. In Table 2 , it can be seen that the accuracy of the numerical results is increased along with the number of grid points. In Fig. 3, we are also depicted the of numerical solutions \( Z_{1} \) and \( Z_{2} \) in the form of 3D graph for \( (a) \alpha _{1}=0.5, \beta _{1}=0.5\), (b) \( \alpha _{1}=0.75, \beta _{1}=0.75\) and (c) \( \alpha _{1}=1.00, \beta _{1}=1.00\) at time \( T=1 \). Authors have discussed the numerical solutions of the equation with the different set of data; for comparison purpose, we refer to [8, 28, 30]. Furthermore, it is found that the results obtained by the proposed method show very good agreement with published results. Moreover, proposed method has obtained the ninth order of accuracy.
7 Conclusion
In this paper, time–space Chebyshev pseudospectral method has been successfully employed to time- and space-fractional coupled Burgers’ equation. The fractional-order differentiation matrix has been established using Caputo–Riemann–Liouville derivative formula at CGL points for fractional-order derivative. It has shown that the numerical results of the proposed method are more close to exact solution. For the equation, convergence analysis of the proposed method has been presented. To demonstrate the performance, the method has been employed two test problems, first for time-fractional and other for space-fractional coupled Burgers’ equation. Reported numerical results are highly accurate which shows the efficiency of the proposed method.
References
Ahmed, H.F.; Bahgat, M.; Zaki, M.: Analytical approaches to space-and time-fractional coupled burgers’ equations. Pramana 92(3), 38 (2019)
Alam Khan, N.; Ara, A.; Mahmood, A.: Numerical solutions of time-fractional burgers equations: a comparison between generalized differential transformation technique and homotopy perturbation method. Int. J. Numer. Methods Heat Fluid Flow 22(2), 175–193 (2012)
Asgari, Z.; Hosseini, S.: Efficient numerical schemes for the solution of generalized time fractional burgers type equations. Numer. Algorithm 77(3), 763–792 (2018)
Balyan, L.K.; Mittal, A.K.; Kumar, M.; Choube, M.: Stability analysis and highly accurate numerical approximation of fisher’s equations using pseudospectral method. Math. Comput. Simul. 177, 86–104 (2020)
Benton, E.R.; Platzman, G.W.: A table of solutions of the one-dimensional burgers equation. Q. Appl. Math. 30(2), 195–212 (1972)
Cao, W.; Xu, Q.; Zheng, Z.: Solution of two-dimensional time-fractional burgers equation with high and low reynolds numbers. Adv. Differ. Equ. 2017(1), 338 (2017)
Cenesiz, Y.; Baleanu, D.; Kurt, A.; Tasbozan, O.: New exact solutions of burgers’ type equations with conformable derivative. Wave Random Compl. Media 27, 103–116 (2017)
Chen, Y.; An, H.-L.: Numerical solutions of coupled burgers equations with time-and space-fractional derivatives. Appl. Math. Comput. 200(1), 87–95 (2008)
El-Danaf, T.S.; Hadhoud, A.R.: Parametric spline functions for the solution of the one time fractional burgers’ equation. Appl. Math. Model. 36(10), 4557–4564 (2012)
Emad, A.-B.; Hassan, G.F.: Multi-wave solutions of the space-time fractional burgers and sharma-tasso-olver equations. Ain Shams Eng. J. 7(1), 463–472 (2016)
Esen, A.; Tasbozan, O.: Numerical solution of time fractional burgers equation. Acta Univ. Sapientiae Math. 7(2), 167–185 (2015)
Esen, A.; Tasbozan, O.: Numerical solution of time fractional burgers equation by cubic b-spline finite elements. Mediterr. J. Math. 13(3), 1325–1337 (2016)
Guesmia, A.; Daili, N.: Numerical approximation of fractional burgers equation. Commun. Math. Appl. 1(2), 77–90 (2010)
Inc, M.: The approximate and exact solutions of the space-and time-fractional burgers equations with initial conditions by variational iteration method. J. Math. Anal. Appl. 345(1), 476–484 (2008)
Islam, M.T.; Akbar, M.A.; Azad, M.A.K.: Closed-form travelling wave solutions to the nonlinear space-time fractional coupled burgers’ equations. Arab J. Basic Appl. Sci. 26, 1–11 (2019)
Kurt, A.; Senol, M.; Tasbozan, O.; Chand, M.: Two reliable method for the solution of fractional coupled burgers’ equation arising as a model of polydispersive sedimentation. Appl. Math. Nonlinear Sci. 4(2), 523–534 (2019)
Li, C.; Zeng, F.: Finite difference methods for fractional differential equations. Int. J. Bifurc. Chaos 22(04), 1230014 (2012)
Li, D.; Zhang, C.; Ran, M.: A linear finite difference scheme for generalized time fractional burgers equation. Appl. Math. Model. 40(11–12), 6069–6081 (2016)
Li, L.; Zhou, B.; Chen, X.; Wang, Z.: Convergence and stability of compact finite difference method for nonlinear time fractional reaction-diffusion equations with delay. Appl. Math. Comput. 337, 144–152 (2018)
Mittal, A.: A stable time-space jacobi pseudospectral method for two-dimensional sine-gordon equation. J. Appl. Math. Comput. 63, 1–26 (2020)
Mittal, A.; Balyan, L.: A highly accurate time-space pseudospectral approximation and stability analysis of two dimensional brusselator model for chemical systems. Int. J. Appl. Comput. Math. 5(5), 140 (2019)
Mittal, A.; Balyan, L.; Tiger, D.: An improved pseudospectral approximation of generalized burger-huxley and fitzhugh-nagumo equations. Comput. Methods Differ. Equ. 6(3), 280–294 (2018)
Mohammadizadeh, F.; Tehrani, H.; Georgiev, S.; Noori Skandari, M.: An optimal control problem associated to a class of fractional burgers’ equations. Asian-Eur. J. Math. 2019, 2050079 (2019)
Momani, S.: Non-perturbative analytical solutions of the space-and time-fractional burgers equations. Chaos Solitons Fractals 28(4), 930–937 (2006)
Prakash, A.; Kumar, M.; Sharma, K.K.: Numerical method for solving fractional coupled burgers equations. Appl. Math. Comput. 260, 314–320 (2015)
Rossikhin, Y.A.; Shitikova, M.V.: Application of fractional calculus for dynamic problems of solid mechanics: novel trends and recent results. Appl. Mech. Rev. 63(1), 010801 (2010)
Senol, M.; Tasbozan, O.; Kurt, A.: Numerical solutions of fractional burger’s type equations with conformable derivative. Chin. J. Phys. 58, 75–84 (2019)
Singh, J.; Kumar, D.; Swroop, R.: Numerical solution of time- and space-fractional coupled burgers’ equations via homotopy algorithm. Alex. Eng. J. 55, 1753–1763 (2016a)
Singh, J.; Kumar, D.; Swroop, R.: Numerical solution of time-and space-fractional coupled burgers’ equations via homotopy algorithm. Alex. Eng. J. 55(2), 1753–1763 (2016b)
Yıldırım, A.; Kelleci, A.: Homotopy perturbation method for numerical solutions of coupled burgers equations with time-and space-fractional derivatives. Int. J. Numer. Methods Heat Fluid Flow 20(8), 897–909 (2010)
Yokus, A.; Kaya, D.: Numerical and exact solutions for time fractional burgers’ equation. J. Nonlinear Sci. Appl. 10(7), 3419–3428 (2017)
Zeng, F.; Li, C.; Liu, F.; Turner, I.: The use of finite difference/element approaches for solving the time-fractional subdiffusion equation. SIAM J. Sci. Comput. 35(6), A2976–A3000 (2013)
Zeng, F.; Li, C.; Liu, F.; Turner, I.: Numerical algorithms for time-fractional subdiffusion equation with second-order accuracy. SIAM J. Sci. Comput. 37(1), A55–A78 (2015)
Zhang, J.; Wei, Z.; Yong, L.; Xiao, Y.: Analytical solution for the time fractional bbm-burger equation by using modified residual power series method. Complexity 2018, 8 (2018)
Acknowledgements
The author is highly grateful to the anonymous referee for his comments and suggestions which helped improve the quality of manuscript.
Author information
Authors and Affiliations
Corresponding author
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mittal, A.K. Spectrally accurate approximate solutions and convergence analysis of fractional Burgers’ equation. Arab. J. Math. 9, 633–644 (2020). https://doi.org/10.1007/s40065-020-00286-x
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40065-020-00286-x