Bifurcation in car-following models with time delays and driver and mechanic sensitivities

Abstract

In this work, we study a model of traffic flow along a one-way, one lane, road or street, the so-called car-following problem. We first present a historical evolution of models of this type corresponding to a successive improvement of requirements, to explain some real traffic phenomena. For both mathematical reasons and a better explanation of some of those phenomena, we consider more convenient and accurate requirements which lead to a better non-linear model with reaction delays, from several sources. The model can be written as an ordinary nonlinear delay differential equation. It has equilibrium solutions, which correspond to steady traffic. The mentioned reaction delays introduce perturbation terms in the equation, leading to of instabilities of equilibria and changes of the structure of the solutions. For some of the values of the delays, they may become oscillatory. We make a number of simulations to show these changes for different values of delays. We also show that, for certain values of the delays the above mentioned change of structure (representing regimes of real traffic) corresponds to a Hopf bifurcation.

1 Introduction

In this work we first present some models for traffic flow in which, as usual, there exists among the basic variables some relationships coming from basic and suitable physical laws. The selection of one of such laws or another leads to different models of traffic flow. Besides, we focus on a particular feature of the traffic flow, not very often dealt with, such as the delays involved, important enough to be taken into account to improve significantly the models or to build more realistic and accurate ones. There are some evident delays, as the one caused by an accident, which certainly modify the traffic conditions. For self-driven vehicles, reaction delays tend to be smaller than those of human-driven vehicles, and typically occur due to the delays in sensing some information, processing it and acting. In the context of human-driven vehicles, our investigation on the impact of the reaction delay enhances phenomenological insights into the emergence and evolution of traffic congestion. For example, a peculiar phenomenon as the emergence of a backpropagating congestion wave in motorway traffic, seemingly coming out of nowhere, has been observed in the real world. In traffic, the phenomenon of stop-and-go waves (known as a start-stop waves, or a ‘phantom jam’) has been empirically studied by many authors. Some studies have shown that a change in driver’s sensitivity (for instance, a sudden deceleration) can lead to such oscillatory behavior. Similar oscillations could also result from an increase in the driver’s reaction delay.

When dealing with the delay equations arising in car-following problems, and in order to obtain more refined models, it seems convenient to consider the delay as the total effect of different causes (see [24] among others). One of them is the time between drivers’ perception of changes or hazards ahead, becoming aware of them and acting accordingly. Another part of the reaction time would be the processing of the information, and the actions taken on the mechanisms of the car. It can be seen that the different processes mentioned above lead to different overall amounts of time. However, in modeling, the time spent on each step has a different degree of variability and importance with respect to the others. For example, in certain cases, some of them can be considered constants and the others not. In some models, as in electric cars, the mechanical response is almost immediate and the mechanic delay is almost zero. In some other cases, as in self driven cars, the driver’s delay is usually smaller than the human one.

Concerning the driver, there has been an evolution of models characterized by increasingly sophisticated assumptions about the driver behavior. These models have progressed from the assumption that drivers behave according to the safe following rule, through early assumptions that the distance is based on the reaction time required to perceive the need to decelerate and apply the brakes, to the General Motors’ models (GM) (see e.g. [1]) in which is adopted the assumption that the car-following response (acceleration or deceleration) was a function of a stimulus, represented by the relative velocity of the leading vehicle, and “sensitivity”, which itself is a function of the spacing between vehicles. The search for the large stimulus used by drivers in car-following appears to represent the most concerted effort to explore the psychological factors in car-following. According to [12], the most successful stimulus is the relative speed divided by spacing, and the least successful stimulus is just the spacing between the vehicles. Later models incorporated the possibility that the following drivers may use information from more than one vehicle ahead to anticipate the actions of the leading vehicle. There are further models taking into account several other features, some of them still open, as those considering the comparison of the driver’s estimation of spacing with the actual spacing, or more realistic ones, where the delay may be dependent of the state of the system, such as relative positions or velocities. In some other fields this situation has been considered, as in [3] and in the references therein, mainly [18].

By taking the delay as central in the analysis of the change of stability of the solutions, we can also analyze the time-delayed traffic dynamics in a control problem perspective. In several works, within a large family of problems, the delay is a tool for control (see e.g. [4, 5, 24]).

We then consider a different non-linear car-following model with a reaction delay. For a single lane, it can be written as an ordinary nonlinear delay differential equation defined by a sigmoidal function, to better fit most of mathematically reasonable assumptions taken from real traffic. This new class of traffic-flow models is introduced in Sect. 2. The choice of a family of sigmoidal function has much interest by itself because, due to their properties, they are better adapted to the conditions to be verified by the variables of the new problem we wish to study. Their properties have proved also useful in the study of problems in other important and very different fields, such as the modeling of activation potential in biological neural networks, or where the conditions on the (very different) variables whose relationships are to be modeled are similar. Superposition of certain sets of sigmoidal functions can be used to approximate some other functions of one or several variables in different normed spaces (see, for example, [10]) in order to obtain a best approximation to non sigmoidal models.

We study this new model in Sect. 3. There exists equilibrium solutions which correspond to steady traffic. The reaction delay terms introduce perturbations for this equation and its solutions, which change their structure. We study the stability of these changes. First we look for the roots, and its nature, of the quasi-characteristic equation of the linearized equation (Sect. 3.1). This will give regions of the values of the parameters, mainly the delays, for which to expect different behavior (constant, oscillatory, periodic, etc.). From the numerical point of view (Sect. 3.2), we make simulations for this type of Differential Delay Equation (DDE). We have adapted to this case some numerical methods for differential equations without delays and to first order system of delay differential equations. Our simulations may provide also a way to find suitable values of parameters for a proper behavior of the cars. The simulation studies show changes of structure. In particular, when the delays vary, a phenomenon known as Hopf bifurcation seems to appear (Sect. 4).

2 Some car-following models

Car-following theory is an important research direction in the field of intelligent transportation systems. It describes the one-by-one following process of vehicles on the same lane in traffic flow, and one of its important issues is congestion control. The follow-the-leader theory of traffic is a theory pertaining to single-lane dense traffic with no passing, and is based on the assumption that each driver reacts in some specific way to a stimulus from the car (or cars) ahead of and/or behind him.

There are different ways towards the modeling of traffic flow:

Macroscopic models where traffic is viewed as a compressible fluid formed by vehicles. The traffic flow can be characterized by macroscopic parameters like the mean velocity or the mean flow and without inflow from and outflow to other ways: to build these models, it is assumed that the car velocity u is a known function of the density $\rho$, $u=u\left( \rho \right) ,$ and that the total number of cars is conserved. As a consequence, the density and velocity must satisfy a conservation law, the continuity equation in one dimension

$$\begin{aligned} \partial _{t}\rho +\partial _{x}(\rho u)=0. \end{aligned}$$

These models lead to (hyperbolic) partial differential equations, [2, 20], among others, and references therein.

Microscopic models where an individual vehicle is represented by a particle and the vehicle traffic is treated as a system of interacting particles driven far from equilibrium. The traffic flow can be considered as the motion of a single particle (vehicle) known as the microscopic approach (e. g. see [15]).

Car-following model is based on the idea that each driver controls a vehicle under the stimuli from the preceding vehicle, which can be expressed by a function of the headway distance or the relative velocity of two successive cars. The models introduce a delay term associated to the driver reaction. The basic differential difference equations of the follow-the-leader theory express the idea that each driver of a vehicle responds to a given stimulus according to a relation such as

$$\begin{aligned} \text {response}=\text {sensitivity}\propto \text {stimulus}. \end{aligned}$$

Car-following models are commonly classified into classes depending on the logic used:

• (i) Gazis–Herman–Rothery models (GM). These models state that the following vehicle’s acceleration is proportional to the speed of the follower, the speed difference between follower and leader and the space in between (see [1, 15]).

• (ii) Safety-distance models, which are based on the assumption that the follower always keeps a safe distance to the vehicle in front (see [12]).

• (iii) Psycho-physical car-following models, which use thresholds for, e. g., the minimum speed difference between follower and leader perceived by the follower (see [24]).

Traffic micro-simulation models are commonly used to estimate macroscopic traffic measures. The response has been taken as the acceleration of the vehicle, since a driver actually has a direct control of this quantity through the gas and brake pedals. The stimulus could be a functional of the positions of a number of cars and their speed, and, perhaps, also some other parameters (this may lead to linear or nonlinear models). The sensitivity was initially taken as a constant and later as inversely proportional to the spacing of the leading and following car. Other functionals for the sensitivity can be considered. The various modifications of the sensitivity functional have been made, in general, as attempts to account for experimental and observational data. These have been obtained from both phenomenological observations on a single-lane traffic flow in tunnels (there are some classical experiments in the Lincoln Tunnel of New York [15]) and from other follow-the-leader experiments.

In this work, by taking into account the driver’s reaction time, the resulting model is a family of functional differential equations with, a parameters dependent, sigmoidal function. We study the stability of the equilibrium state by investigating the location of the roots of the quasi-characteristic equation. We carry out both numerical and graphical simulations. This gives us regions of values of the parameters for which the equilibrium solution changes its stability modifying its structure and giving rise, eventually, to some kind of oscillatory and periodic solutions.

2.1 A follow-the-leader General Motors’ model (GM)

In this subsection we present and analyze some previous car-following models built from a follow-the-leader General Model (GM). Let us consider a car following another, under the following assumptions:

• (i) The cars flow on a single lane.

• (ii) If t is the time (assuming that the initial time $t_{0}=0$), for the car n at the time t,  $X_{n}\left( t\right)$ is its position, $X_{n}^{\prime }(t)$ is its velocity,  and $X_{n}^{\prime \prime }(t)$ is its acceleration.

• (iii) The driver n (following car) adjust his speed with respect to the speed of the car $n+1$ (the leading car).

• (iv) There exist a time lag $\tau _{ {n}}$ reaction of the following car to the actions of the leading car. As said above,

  $$\begin{aligned} \tau _{ {n}}=\tau _{d_{ {n}}}+\tau _{m_{ {n}}} \end{aligned}$$

  with $\tau _{d_{ {n}}}$ is the reaction delay of the driver and $\tau _{m_{ {n}}}$ is the mechanic delay of his car.

A first analysis is to consider that the acceleration (or deceleration) of car n is proportional to the perceived difference with respect to car $n+1$. Mathematically,

$$\begin{aligned} X_{n}^{\prime \prime }\left( t+\tau _{ {n}}\right) =u\left( X_{n+1}^{\prime }\left( t\right) -X_{n}^{\prime }\left( t\right) \right) . \end{aligned}$$

Now we can distinguish if u is a constant or a nonconstant function depending, for instance, of the distance between cars, the relative velocity, etc.

When u is a constant function, the car-following model is linear. In this case, the acceleration (response) is directly proportional to the relative velocity (stimulus) (see [8]).

When u is a nonconstant function, the car-following model is nonlinear. Several relationships can be considered, usually a certain power (to be determined) of the following car’s speed. Moreover, Gazis et al. [14] found that the above equation could not quite explain the traffic situation in higher density since, in it, the behavior of the drivers that follows does not just take into account the relative spacing between cars. In order to make the model more realistic, they defined u as a real function of the distance between two cars, that is $u =u\left( X_{n+1}\left( t\right) -X_{n}\left( t\right) \right)$, and choosing u as

$$\begin{aligned} u=c\frac{1}{X_{n+1}\left( t\right) -X_{n}\left( t\right) }, \end{aligned}$$

which implies

$$\begin{aligned} X_{n}^{\prime \prime }\left( t+\tau _{ {n}}\right) =c\frac{1}{X_{n+1}\left( t\right) -X_{n}\left( t\right) }\left( X_{n+1}^{\prime }\left( t\right) -X_{n}^{\prime }\left( t\right) \right) \end{aligned}$$

In 1961, Edie (see [11]) modified the model again and considered that the velocity of vehicle itself also influence the behavior of driver. In consequence, the GM model can be expressed, more generally, as

$$\begin{aligned} X_{n}^{\prime \prime }\left( t+\tau _{ {n}}\right) =c\frac{X_{n}^{\prime }\left( t\right) ^{m}}{\left( X_{n+1}\left( t\right) -X_{n}\left( t\right) \right) ^{l}}\left( X_{n+1}^{\prime }\left( t\right) -X_{n}^{\prime }\left( t\right) \right) \end{aligned}$$

(1)

where m and $l\in \mathbb {R}$ are nonnegative constants to be determined by experimental data. The key to the selection of a model from this set of models (GM), is the specification of parameters m and l. In the following years, a large amount of work on the definition of the ‘best’ combination of m and l was done, but without a uniform result (see Table 1).

Table 1 Models according to different values of m and l (see [1] and its references)

However, in these models, the distance between successive vehicles can be arbitrarily close when the leading and the following vehicles have identical speed, which seems to be somewhat unrealistic. This is one of the reason why we propose a refined new class of traffic-following models (see [7]) defined by a sigmoidal function.

2.2 A new car-following model as a Delay Differential Equation (nDDE)

We introduce a multiparameter car-following model defined by a specific class of functions avoiding the above inconvenient and satisfying the other requirements. In this car traffic situation, we will focus our attention only in two cars, one leader and its follower. We introduce a new notation. Let us consider that, at the instant t,  $X_{ 0}\left( t\right)$ is the position of the leading car and $X_{ 1 }\left( t\right)$ is that of the following car. We assume that the velocity of the leading car (i. e. $X_{ 0}^{\prime }\left( t\right)$) is a given positive constant $v_{0}$. Thus, $X_{0}(t) = v_0t + x_0$, with $x_0$ its initial position that, without loss of generality, we can assume as $x_0 = 0$.

Let us define the separation between the cars as

$$\begin{aligned} s_1\left( t\right) =X_{ 0}\left( t\right) -X_{ 1}\left( t\right) =v_{0}t-X_{ 1}\left( t\right) . \end{aligned}$$

Thus, the relative velocity and the relative acceleration of the following car are

$$\begin{aligned} s_1^{\prime }\left( t\right) =v_{0}-X_{ 1}^{\prime }\left( t\right) \;\;\;\;\;\text {and}\;\;\;\;\;s_1^{\prime \prime }\left( t\right) =-X_{ 1} ^{\prime \prime }\left( t\right) . \end{aligned}$$

Combining those relations with the car-following differential equation, we obtain from (1) a second order delay differential equation in terms of the separation between the cars and relative velocity, that is,

$$\begin{aligned} -s_1^{\prime \prime }\left( t+\tau _{ 1}\right)&=X_{ 1}^{\prime \prime }\left( t+\tau _{ 1}\right) =cX_{ 1}^{\prime }\left( t\right) ^{m}\frac{X_{ 0}^{\prime }\left( t\right) -X_{ 1}^{\prime }\left( t\right) }{\left( X_{ 0}\left( t\right) -X_{ 1}\left( t\right) \right) ^{l}}\\ s_1^{\prime \prime }\left( t+\tau _{ 1}\right)&=-c\left( v_{0}-s_1^{\prime }\left( t\right) \right) ^{m}\frac{s_1^{\prime }\left( t\right) }{s_1\left( t\right) ^{l}} \end{aligned}$$

Notice that $s_1''$ is a function of $(v_0,s_1(t),s_1'(t))$ and then the above delay equation is autonomous. This allow us to study the changes of structure of solutions as a Hopf Bifurcation problem for these equations.

Remark 1

If we assume that the velocity of the leader is not a constant (we can consider that $X_0'(t)$ is a data of the problem and so is its acceleration $X_0''(t)$), then the relative velocity and the relative acceleration of the following car are

$$\begin{aligned} s_1^{\prime }\left( t\right) =X_{0}'(t)-X_{ 1}^{\prime }\left( t\right) \;\;\;\;\;\text {and}\;\;\;\;\;s_1^{\prime \prime }\left( t\right) =X_{0}''(t)-X_{ 1} ^{\prime \prime }\left( t\right) . \end{aligned}$$

Combining those relations with the car-following differential equation, we obtain from (1), as before, a second order delay differential equation in terms of the separation between the cars, the relative velocity and also the velocity and acceleration of the leader, that is,

$$\begin{aligned} s_1^{\prime \prime }\left( t+\tau _{ 1}\right)&=-c\left( X_{0}'(t)-s_1^{\prime }\left( t\right) \right) ^{m}\frac{s_1^{\prime }\left( t\right) }{s_1\left( t\right) ^{l}} + X_{0}''(t+\tau _1). \end{aligned}$$

(notice that $s_1''$ is function of $(t,\tau _1 ,s_1(t),s_1'(t))$, and then the above delay equation is non autonomous).

Remark 2

For several cars, assuming that the leader has a constant velocity $v_0$ and the rest of the cars adapt their velocities to their corresponding leaders, we can obtain the following system:

$$\begin{aligned} s_1^{\prime \prime }\left( t+\tau _{ 1}\right)&=-c\left( v_{0}-s_1^{\prime }\left( t\right) \right) ^{m}\frac{s_1^{\prime }\left( t\right) }{s_1\left( t\right) ^{l}} \\&\vdots \\ s_i^{\prime \prime }\left( t+\tau _{ i}\right)&=-c\left( X_{i-1}'(t)-s_1^{\prime }\left( t\right) \right) ^{m}\frac{s_i^{\prime }\left( t\right) }{s_i\left( t\right) ^{l}} + X_{i-1}''(t+\tau _i) \end{aligned}$$

where, for any $i=2,3,\ldots$, $s_{i-1}(t) = X_{i-2}(t)-X_{i-1}(t)$, $X_{i-1}'(t) = X'_{i-2}(t)-s_{i-1}'(t)$, $X_{i-1}''(t) = X''_{i-2}(t)-s_{i-1}''(t)$ (recursively it is possible to get a coupled system in terms of $s_i,s_i',s_i''$ and finally with $v_0$) and $\tau _i$ are the delay for the different vehicles. The purpose of this work is to study the behavior of the two first cars related with the bifurcation phenomenon.

Remark 3

We will only consider two vehicles. The leader goes at a constant velocity $v_0$ and the follower tries to adapt its velocity $X_1'(t)$ to that of the leader, but with a reaction time $\tau _1$. In what follows this is the only reaction time to consider, so we will call $\tau :=\tau _1$. For the same reason, in what follows all function or parameters associated to the follower will appear without any subindex (as, for example, s, the parameters a, b, k, d, ... that will appear later).

We should add some other requirements for the model. For example, $X_{ 0}\left( t\right) -X_{ 1}\left( t\right) =0$ must be avoided. Of course, from the reality, but also because this situation leads to additional an unnecessary mathematical difficulties. So, we consider, in general, that the relative acceleration (deceleration) is a prescribed function of $s\left( t\right) ,s^{\prime }\left( t\right)$, i.e.

$$\begin{aligned} s^{\prime \prime }\left( t+\tau \right) =-g\left( s\left( t\right) ,s^{\prime }\left( t\right) \right) \end{aligned}$$

where the real function $g\left( s,s^{\prime }\right)$ with $\left( s,s^{\prime }\right) \in \mathbb {R}^{2}$ must satisfy some conditions:

• (i) For any $v_{0}\$there exists an m (we will refer to it in Sect. 3.1), minimum recommended distance between cars. We assume that the car following the leader is in an equilibrium state when there is no speed difference with the leading car, that is $s^{\prime }\left( t\right) =0$; and when it follows it at the safe minimum distance $s\left( t\right) =m$, thus the velocity of the following car is constant and then the acceleration is zero, that is $g\left( m,0\right) =0$ at the equilibrium point.

• (ii) There is a maximum acceleration of the following car, $a>0$, thus $g\left( s,s^{\prime }\right) \le a$, and a maximum deceleration, $b<0$, thus $b\le g\left( s,s^{\prime }\right)$. So, $b\le g\left( s,s^{\prime }\right) \le a$ for all $\left( s,s^{\prime }\right) \in \mathbb {R}^{2}$

• (iii) If the relative velocity $s^{\prime }\left( t\right) =0$,

  $$\begin{aligned} X_{ 1}^{\prime \prime }\left( t\right) =g\left( s,0\right) \left\{ \begin{array}{ccc}>0 &{} \text {if} &{} s>m\\ =0 &{} \text {if} &{} s=m\\<0 &{} \text {if} &{} s<m \end{array} \right. . \end{aligned}$$

  If the relative velocity $s^{\prime }\left( t\right) >0$ (increasing the distance between cars), the car that follows would accelerate even when the distance $s(t)<m$. If the relative velocity $s^{\prime }\left( t\right) <0$ (decreasing the distance between cars), the car that follows would decelerate even when the distance $s(t)>m$.

• (iv) Moreover, g is increasing with respect to s.

On the other hand, we want to include in the modeling the temperament of the driver ($d_{driver}$) that follows and that of the mechanic of its vehicle ($d_{mechanic}$), meaning a sort of intensity of the response (in some references this type of parameters are called aggresivity both for the drivers and the cars [23]). We will also take into account a parameter k which determine the driver’s intensity of the action according to the safe distance and the minimum relative velocity which the driver is able to perceive (which is not neither the real relative velocity nor the real safe distance, but the driver’s perception of them). A suitable choice is to take $k=m/w$, where m is the safe minimum distance and w is the relative velocity that the driver can perceive.

As a convenient functions satisfying the above conditions, we consider a class of sigmoidal functions. In particular, we will take a function g of the distance between the cars s and of the speed difference $s^{\prime }$:

$$\begin{aligned} g\left( s,s^{\prime }\right) =a-\frac{\left( a+b\right) }{1+\frac{b}{a}e^{d\left( s-m+ks^{\prime }\right) }},\ \ \forall \left( s,s^{\prime }\right) \in \mathbb {R}^{2}, \end{aligned}$$

(2)

with d a function of $d_{driver}$ and $d_{mechanic}$. For the numerical simulation, we will take $d=1/(d_{driver}\cdot d_{mechanic})$. This choice responds to the effect caused in g by assuming that the higher the temperament (increasing $d_{driver}$ and $d_{mechanic}$) the desired speed is reached in less time (and therefore in space). In the function g, this effect is achieved by making d smaller. Finally our model would be

$$\begin{aligned} s^{\prime \prime }\left( t+\tau \right) =-g\left( s\left( t\right) ,s^{\prime }\left( t\right) \right) =-a+\frac{\left( a+b\right) }{1+\frac{b}{a}e^{d\left( s\left( t\right) -m+ks^{\prime }\left( t\right) \right) }}. \end{aligned}$$

(3)

In the rest of the text we will refer to this model by nDDE (new car-following traffic model). For the Eq. (3) in the next sections we study the stability of constant solutions, linearizing the equation and studying its quasi-characteristic roots and we obtain numerical and graphical simulations. We find certain values for the delay parameter for which it is possible to control the change of structure of the solutions of the equation, from constant to oscillatory and a Hopf bifurcation. These results of transition from constant to oscillatory behavior, would correspond to the transition of steady traffic to the above mentioned phantom jam phenomenon.

3 Analysis and simulation for the nDDE model

3.1 Quasi-characteristic equation of the linearized equation

We assume that in the equilibrium point, $s=m$ and $s^{\prime }=0$, the influence of $s^{\prime }$ was to move the sigmoid left or right. Also, the sigmoid keeps the same shape and that the relationship between s and $s^{\prime }$ is linear. To study the stability of the equilibrium point we will study the linearized equation in the neighborhood of $s=m$ and $s^{\prime }=0$.

Taking $x=\sigma -m+k\omega$ and $\tilde{g}\left( x\right) =g\left( \sigma ,\omega \right)$, the McLaurin series in $x=0$ of $\tilde{g}$ is $\tilde{g}\left( x\right) =d\frac{ab}{a+b}x+O\left( x^{2}\right)$. In particular

$$\begin{aligned} g\left( \sigma ,\omega \right) =d\frac{ab}{a+b}\left( \sigma -m+k\omega \right) +\text {Higher Order Terms} \end{aligned}$$

Considering the McLaurin series of $\tilde{g}\left( x\right)$ ($=g\left( \sigma ,\omega \right)$) in (3)

$$\begin{aligned} s^{\prime \prime }\left( t+\tau \right) \!&=-\tilde{g}\left( s\left( t\right) -m+ks^{\prime }\left( t\right) \right) +\text {Higher Order Terms}\\&=-d\frac{ab}{a+b}\left( s\left( t\right) -m+ks^{\prime }\left( t\right) \right) +\text {Higher Order Terms} \end{aligned}$$

Making the change of variables $S=s-m$ and renaming the coefficients, we obtain

$$\begin{aligned} S^{\prime \prime }\left( t+\tau \right) =-DKS^{\prime }\left( t\right) -DS\left( t\right) \end{aligned}$$

(4)

with $D=d\frac{ab}{a+b}$ and $K=k$. The quasi-characteristic equation for this delay equation is

$$\begin{aligned} w^{2}e^{w\tau }+DKw+D=0. \end{aligned}$$

(5)

Finally, making $u=w\tau$ we obtain

$$\begin{aligned} u^{2}e^{u}+DK\tau u+D\tau ^{2}=0. \end{aligned}$$

To study stability of the equilibrium position, we analyze the real and imaginary parts of the roots. We write $u=x+iy$, and the above transcendental equation can be written, separating the real and imaginary parts as

$$\begin{aligned} 0&= \left( (x^{2}-y^{2})\cos (y)-2xy\sin (y)\right) e^{x}+D\tau ^{2}+DK\tau x\\&\quad +[\left( (x^{2}-y^{2})\sin (y)+2xy\cos (y)\right) e^{x}+DK\tau y]i. \end{aligned}$$

We represent the curves of real and imaginary parts equal to zero for different values of the parameters

$$\begin{aligned}&\left( (x^{2}-y^{2})\cos \left( y\right) -2xy\sin \left( y\right) \right) e^{x}+D\tau ^{2}+DK\tau x =0, \end{aligned}$$

$$\begin{aligned}&\left( (x^{2}-y^{2})\sin (y)+2xy\cos (y)\right) e^{x}+DK\tau y =0. \end{aligned}$$

(6)

The above system has infinite solutions. The solutions u of this system are complex functions of $\tau$, that is, $u=u\left( \tau \right)$. We are interested in non constant solutions u corresponding to real part negative ($x\left( \tau \right) <0$) which are stable oscillating solutions. When the real part is positive ($x\left( \tau \right) >0$) we have unstable oscillating solutions and finally for real part equal to zero ($x\left( \tau \right) =0$) they are periodic solutions.

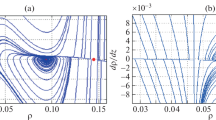
For the numerical simulation, we will take a particular case of g corresponding to the following parameters: $a=2.0576$ m/s$^{2}$, $b=1.5677\,\mathrm {m/s}^{2}$, $d=0.1124$, $m=44.4444\,\mathrm {m}$, $k=m/w=11.389 0\,\mathrm{s}\ (w=3.9 {024}$ m/s). For the simulation we consider that $d_{mechanic}=d_{driver}=2.9829$ and thus $d=0.1124$. Thus $D=0.1 {000}$ and $K=11.3890$. We study the graphical solutions for different values of $\tau$ for the last system. Given $\tau _{0}>0$ small enough, we fix our attention in a root of the (6) close to the origin. Graphically (see Fig. 1), we can see how the root moves in such a way that its real part changes from negative value (left graphic) to positive one (right graphic) when $\tau >\tau _{0}$ increases.

Fig. 1

Graphics of solutions of the system (6) for two delay time values

So, the variation of the roots when $\tau$ varies may lead to a change of the structure of the solutions because the real part function $x\left( \tau \right)$ crosses the imaginary axes. This change of structure suggests the appearance of the phenomenon known as Hopf bifurcation (Sect. 4). In the next section we show numerical solutions for the nDDE (3).

3.2 Numerical simulation. Structure of solutions

For the numerical study of the nonlinear initial value problem for the nDDE (3), we give initial values (functions, since we are dealing with a delay differential equations) for the separation of the car $s_{0}\left( t\right)$ and the relative velocity $s_{0}^{\prime }\left( t\right)$ in the interval $t\in [-\tau ,0]$, obtained the nonlinear initial value problem

$$\begin{aligned} s^{\prime \prime }\left( t+\tau \right)&=-g\left( s^{\prime }\left( t\right) ,s\left( t\right) \right) ,\ \ t\ge 0 \end{aligned}$$

(7)

$$\begin{aligned} {{\phi }(\theta ) }&= {{\phi }_0(\theta ), \quad \theta \in [-\tau ,0] } \end{aligned}$$

(8)

with ${\phi }(\theta ) := \left( \begin{array}{c} s\\ s' \end{array} \right) (\theta )$ and ${\phi }_0(\theta ) := \left( \begin{array}{c} s_0\\ s_0' \end{array} \right) (\theta )$, regular enough. Under the regularity conditions, the results of existence, uniquenes and continuous dependence on the initial data and forward continuation are fulfilled [17]. We are interested in the behaviour of solutions for large values of time. We consider the sigmoidal function g defined in (2) given by specific values of the parameters taking in Sect. 3.1. These test values comes from experimental data and those which allow to improve the graphic visibility of the behavior of the solution (see e.g. [13] and its references). We use the code dde23 of Matlab R2018a for the numerical simulation. For the numerical simulation, we fix a constant velocity of the leader car, $v_0$, at 80 km/h $=22.2222$ m/s and for the follower, its velocity is 100 km/h $= 27.7778$ m/s constant in $[-\tau , 0]$. Thus, the relative velocity $s'(\theta ) = X'_0(\theta )-X'_1(\theta ) = -5.5556$ m/s for any $\theta \in [-\tau , 0]$. On the other hand, the initial distance between vehicles it was taken at 20m plus the safety distance $m = 44.4444$ m. So, the initial function distance will be $s(\theta ) = (20 + m) + s'(\theta )\theta = 64.4444 - 5.5556\theta$ for all $\theta \in [-\tau , 0]$. That is

$$\begin{aligned} \phi _0(\theta ) = \left( \begin{array}{c} 64.4444 - 5.5556\,\theta \\ -5.5556 \end{array} \right) , \quad \theta \in [-\tau ,0] . \end{aligned}$$

(9)

For different values of time delay $\tau >0$ and fixing for any of them the same initial functional data (9) and the parameters stated above, we obtain the following graphic solutions (see Figs. 2, 3).

Fig. 2

Delay time $\tau =1.2$ s. The solution is oscilatory and stable. The follower keeps always positive distances from the leader ($0<s\left( t\right) \approx m$ for large t)

Fig. 3

Delay time $\tau =6.5$ s. The solution is oscillatory and unstable. Mathematically the oscillations increase their amplitude. The follower hit the leader at some time

Each graphic have three parts: (a) is the graphic of the s, $s^{\prime }$ and $s^{\prime \prime }$ with respect to time; (b) show the 2D-curve $\left( s^{\prime },s^{\prime \prime }\right)$ and (c) the 3D-curve $\left( s,s^{\prime },s^{\prime \prime }\right)$. We can see for the stable cases, that the curve $\left( s^{\prime },s^{\prime \prime }\right)$ converges to the equilibrium point $\left( 0,0\right)$. The curve $\left( s,s^{\prime },s^{\prime \prime }\right)$ also converges to the equilibrium point $\left( m,0,0\right)$. On the other hand, we can see how the curve $\left( s,s^{\prime },s^{\prime \prime }\right)$ locally lies in the plane defined by the linear part of the nDDE (4). For the unstable case the curve $\left( s,s^{\prime },s^{\prime \prime }\right)$ goes away from the plane after a large time.

The simulation studies show interesting effects on the dynamics of solutions of the system associated to our car-following model. In particular, there are changes of structure in its solutions as the delays vary. There are equilibrium states of the system, stable or unstable, and as the delay vary, a given equilibrium, a stable solution, may loss its stability and other equilibria may branch off. Very often this happens to constant solutions which lead to time periodic oscillations. This way to appear these nonconstant solutions is a phenomenon known as Hopf bifurcation. Depending on the type of dynamical system, the formulation of such a phenomenon takes different forms (see, for example, [9, 19, 21, 22]). The study of bifurcation could be considered from different points of view as, for example, by using the Poincaré–Lindstedt method (see e. g. [6]) which might allow to find a series expansion of the periodic solutions in powers of the delay. Here we will base our study on the method used by, for instance, in [16, Ch. 11, Section 1.1]. We study this phenomenon in the next section.

4 Hopf bifurcation

The equation of the model in this work (7) can be considered as an example of what is called a Retarded Functional Differential Equation (RFDE). One definition of these equations in one of their proper settings can be found in Hale [16] or Lunel and Hale [17]. To the study of the bifurcation, we will refer and state the Hopf Bifurcation Theorem as in Hale [16, Theorem 1.1, p. 246].

Let $\mathbb {R}^{n}$ the n-dimensional linear vector space over the real numbers with euclidean norm $\left| \cdot \right|$, $C(\left[ a,b\right] ,\ \mathbb {R}^{n})$ is the Banach space of continuous functions mapping the interval $\left[ a,b\right]$ into $\mathbb {R}^{n}$ with the topology of uniform convergence. Consider a given number $\tau \in \mathbb {R}$, $\tau >0$ and let $\mathcal {C}:= C([-\tau ,0],\mathbb {R}^{n})$ and the norm of an element $\varvec{\phi }\in \mathcal {C}$ by $\Vert \varvec{\phi }\Vert =\sup _{-\tau \le \theta \le 0}\vert \varvec{\phi }(\theta )\vert$.

Given two real numbers $\sigma ,$ $A\ge 0\$and $\mathbf {x}\in C(\left[ \sigma -\tau ,\sigma +A\right] ,\mathbb {R}^{n})$, then for any $t\in \left[ \sigma ,\sigma +A\right]$ we define $\mathbf {x}_{t}(\theta )=\mathbf {x} (t+\theta )$ with $\theta \in [-\tau ,0]$. Given $\mathcal {D}$ a subset of $\mathbb {R}\times \mathcal {C}$, we consider the functional $\mathbf {F} :\mathcal {D\subset }\mathbb {R}\times C([-\tau ,0],\mathbb {R}^{n})\rightarrow \mathbb {R}^{n}$ such that

$$\begin{aligned} \frac{d}{dt^{+}}\mathbf {x}\left( t\right) =\mathbf {F}(\tau ,\mathbf {x} _{t}) \end{aligned}$$

(10)

where $\frac{d}{dt^{+}}$ represents the right-hand derivative, and in the following we denote by $\mathbf {x}'= \frac{d}{dt^{+}} \mathbf {x}$. We say that the relation (10) is a Retarded Functional Differential Equation on $\mathcal {D}$, a RFDE associated with $\mathbf {F}$ (we denote by RFDE($\mathbf {F}$) if we need to emphasize the equation is defined by $\mathbf {F}$).

Definition 1

Given $\tau >0$ and $\mathcal {C}:=C {^2}([-\tau ,0],\mathbb {R} ^{n})$, a function $\mathbf {x}$ is said to be a solution of the Retarded Functional Differential Equation (10) on $\mathcal {D\subset }\mathbb {R}\times \mathcal {C}$ for a given functional $\mathbf {F} :\mathcal {D}\rightarrow \mathbb {R}^{n}$, if there are $\sigma \$and $A\ge 0$, such that $\mathbf {x}\in C {^2}(\left[ \sigma -\tau ,\sigma +A\right] ,\mathbb {R} ^{n}),$ $(t,\mathbf {x}_{t})\in \mathcal {D}$ and $\mathbf {x}$ satisfies Eq. (10) for any $t\in \left[ \sigma ,\sigma +A\right]$.

In the same framework as in Definition 1, we introduce the

Definition 2

[IVP] For given $\sigma \ge 0$, $\varvec{\phi }\in \mathcal {C}$, we say that $\mathbf {x}(\sigma ,\varvec{\phi },\mathbf {F})$ is a solution of the initial value problem for the Retarded Functional Differential Equation (10) on $\mathcal {D\subset }\mathbb {R} \times \mathcal {C}$ for a given functional $\mathbf {F}: \mathcal {D} \rightarrow \mathbb {R}^{n}$, with initial value $\varvec{\phi }$ at $\sigma$, or a solution through $(\sigma ,\varvec{\phi } )$, if there is a real number $A\ge 0$ such that $\mathbf {x}(\sigma ,\varvec{\phi },\mathbf {F})$ is a solution of Eq. (10) on $[\sigma -\tau ,\ \sigma +A)$ and $\mathbf {x}_{\sigma }(\sigma ,\varvec{\phi },\mathbf {F})=\varvec{\phi }$.

In this sense, solutions of RFDE could be viewed as curves in a Banach space. In the above mentioned references [16] and [17], suitable definitions and results of the fundamental theory, such as those on existence, uniqueness, continuous dependence and differentiability on data and parameters, regularity with respect to initial conditions and continuation are given (in these equations is important to distinguish between forward and backwards continuation). Answers on these questions depend of the regularity of the above function $\mathbf {F}$.

We recall the formulation of the Hopf bifurcation Theorem 1.1 of [16] for RFDE (10). Let $\mathbf {F}$ be of class $k\ge 2,\mathbf {F}\left( \tau , \mathbf {0}\right) = \mathbf {0}$ for all $\tau \in \mathbb {R}$, $\mathcal {C}:=C\left( \left[ -\tau ,0\right] ,\mathbb {R} ^{n}\right)$ and $\mathbf {x}_{t}(\theta )=\mathbf {x}(t+\theta )$ with $\theta \in [-\tau ,0]$. Define $\mathbf {L}:\mathbb {R}\times \mathcal {C\rightarrow }\mathbb {R}^{n}$ by

$$\begin{aligned} \mathbf {L}\left( \tau \right) \psi =\mathbf {F}_{\phi }\left( \tau ,\mathbf {0}\right) \psi \end{aligned}$$

(11)

with $\psi \in \mathcal {C}$, where $\mathbf {F}_{\phi }\left( \tau ,\mathbf {0}\right)$ is the derivative of $\mathbf {F}\left( \tau ,\phi \right)$ with respecto to $\phi \in \mathcal {C}$ at $\phi =0$ and define

$$\begin{aligned} f\left( \tau ,\phi \right) = \mathbf {F}\left( \tau ,{\phi }\right) - \mathbf {L}\left( \tau \right) \phi . \end{aligned}$$

We have to consider also the following hypotheses:

• (H1) The linear RFDE($\mathbf {L}\left( 0\right)$) (that is, $\mathbf {x}' =\mathbf {F}_{\phi }\left( 0,\mathbf {0}\right) \mathbf {x}_{t}$) has a simple purely imaginary characteristic root $u_{0}=y_{0}i\ne 0$ and all characteristic roots $u (u=x+yi)$ are different of $u_{0}$, $\overline{u}_{0}$ (conjugate of $u_{0}$) and satisfy $u \ne hu_{0}$ for any integer h.

By Lemma 2.2 of Section 7.2 of [16], There exist $\tau _{0}>0$ and simple characteristic root $u\left( \tau \right)$ of the linear RFDE($\mathbf {L}\left( \tau \right)$) (that is, $\mathbf {x}^{\prime }=\mathbf {F}_{\phi }\left( \tau ,\mathbf {0}\right) \mathbf {x}_{t}$) such that has a continuous derivative $u^{\prime }\left( \tau \right)$ for $\vert \tau \vert <\tau _{0}$. Moreover, we assume that

• (H2) ${\text {Re}}(u^{\prime }(0))\ne 0$ (transversality condition).

We introduce the additional notation of [16], to make the statement of the result more specific. By taking $\tau _{0}$ sufficiently small, we may assume ${\text {Im}}u\left( \tau \right) \ne 0$ for $\vert \tau \vert <\tau _{0}$ and obtain a function $\phi _{\tau }\in \mathcal {C}$ which is continuosly differentiable in $\tau$ and allows to define a basis for the solutions of the RFDE($\mathbf {L}\left( \tau \right)$) corresponding to $u\left( \tau \right)$. The functions

$$\begin{aligned} \Phi _{\tau }:=\left( {\text {Re}}\phi _{\tau },{\text {Im}} \phi _{\tau }\right) \end{aligned}$$

form a corresponding basis for the characteristic roots $u_{0}\left( \tau \right)$, $\overline{u}_{0}\left( \tau \right)$. Similarly, a basis $\Psi _{\tau }$ for the adjoint equation can be obtained, with $\left\langle \Psi _{\tau },\Phi _{\tau }\right\rangle =I$. Decomposing $\mathcal {C}$ by $\left( u_{0}\left( \tau \right) ,\overline{u}_{0}\left( \tau \right) \right)$ as $\mathcal {C=P}_{\tau }\oplus Q_{\tau }$, then $\Phi _{\tau }$ is a basis for $\mathcal {P}_{\tau }$. We know that

$$\begin{aligned} \Phi _{\tau }\left( \theta \right) =\Phi _{\tau }\left( 0\right) \exp B\left( \tau \right) \theta ,\ \ \ -\tau \le \theta \le 0, \end{aligned}$$

and the eigenvalues of the $2\times 2$ matrix $B\left( \tau \right)$ are $u_{0}\left( \tau \right)$ and $\overline{u}_{0}\left( \tau \right)$. By a change of coordinates and maybe redefining the parameter $\tau$ we may assume that

$$\begin{aligned} B\left( \tau \right) =y_{0}B_{0}+\tau B_{1}\left( \tau \right) \end{aligned}$$

with

where $\gamma \left( \tau \right)$ is continuosly differentiable on $0\le \left| \tau \right| <\tau _{0}$. We can now state the Hopf bifurcation theorem and we refer to the conclusions stated in this theorem as a Hopf Bifurcation.

Theorem 1

[16, Theorem 1.1, p. 246] Suppose $F\left( \tau ,\phi \right)$ has continuous first derivatives with respect to $\tau ,\phi$, $F\left( \tau ,0\right) =0$ for all $\tau$ and Hypothesis (H1) and (H2) are satisfied. Then there are constants $a_{0}>0,$ $\tau _{0}>0,$ $\delta _{0}>0,$ functions $\tau \left( a\right) \in \mathbb {R}$, $\omega \left( a\right) \in \mathbb {R}$, and an $\omega \left( a\right) -$periodic function $x^{*}\left( a\right)$, with all functions being continuously differentiable in a for $\left| a\right| <a_{0}$, such that $\ x^{*}\left( a\right)$ is a solution of Eq. (10) with

$$\begin{aligned} x_{0}^{*}\left( a\right) ^{P_{\tau }}=\Phi _{\tau \left( a\right) }y^{*}\left( a\right) ,\ \ \ \ \ x_{0}^{*}\left( a\right) ^{Q_{\tau }}=z_{0}^{*}\left( a\right) \end{aligned}$$

where $y^{*}\left( a\right) ={\text {col}}\left( a,0\right) +o\left( \left| a\right| \right)$, $z_{0}^{*}\left( a\right) =o\left( \left| a\right| \right)$ as $\left| a\right| \longrightarrow 0$. Furthermore, for $\vert \tau \vert <\tau _{0}$, $\vert \omega -\left( 2\pi /y_{0}\right) \vert <\delta _{0}$, every $\omega -$periodic solution of equation (10) with $\Vert x_{t}\Vert <\delta _{0}$ must be of the above type except for a translation in phase.

Our particular car-following modeling has led us to a RFDE in which the delay $\tau$ is a parameter including, namely, the different reaction times corresponding to the drivers, to the mechanic of the cars and to some others related to them. Our interest is to give an explanation on how the structure of the solutions can change, from constant to oscillatory solutions, when the delay parameter varies. To do that, we will write the second order delay differential equation (7) in the form of first order delay system (10). As usual, we introduce two functions $z_{1}\left( t\right) =s\left( t\right) -m$ and $z_{2}\left( t\right) =s^{\prime }\left( t\right)$. We rescale the time by making $\bar{t}=t+\tau$, and we rename $\bar{t}$ as t obtaining the equivalent system

$$\begin{aligned} \left\{ \begin{array}{ccl} z_{1}^{\prime }\left( t\right) &{} = &{} z_{2}\left( t\right) \\ z_{2}^{\prime }\left( t\right) &{} = &{} -g\left( z_{1}(t-\tau )+m,z_{2}\left( t-\tau \right) \right) . \end{array} \right. \end{aligned}$$

As before, let us consider the RFDE with

$$\begin{aligned} \mathbf {F}:\mathcal {D\subset }\mathbb {R}&\times C {^2}([-\tau ,0],\mathbb {R} ^{2})\mathcal {\rightarrow }\mathbb {R}^{2} \end{aligned}$$

(12)

$$\begin{aligned} \mathbf {F}\left( \sigma ,\mathbf {z}_{t}\right)&=\left( z_{2_t},-g\left( z_{1_t}+m,z_{2_t}\right) \right) \end{aligned}$$

(13)

with $\sigma \in \mathbb {R}$, $\mathbf {z}=\left( z_{1},z_{2}\right) \in C {^2}([-\tau ,0],\mathbb {R}^{2})$ and $z_{i_t}(t)=z_i(t+\theta )$, $\theta \in [-\sigma , 0]$, $i=1,2$.

By the definition of g, notice that $\mathbf {F}\left( \sigma ,{\phi }\right)$ has a continuous first and second continuous derivatives in ${\phi }$ for all $\sigma$ real and ${\phi }$ in $\mathcal {C} :=C {^2}([-\tau ,0],\mathbb {R}^{2})$ and $\mathbf {F}(\sigma ,\mathbf {0})=\mathbf {0}$ for all $\sigma >0$ (notice that $\mathbf {0}=(0,0)$ is the equilibrium point for (13) and (m, 0) is the equilibrium point for (7) and that $g(m,0) = 0$). These properties on $\mathbf {F}$ and the initial condition (8) ensure affirmative and convenient answers to the basic fundamental theory [16, Chap. 2].

Theorem 2

For $\mathbf {F}$ defined in (13), there exists $\tau _{0}>0$ such that the problem RFDE (8), (10) for this $\tau _0$ has a periodic solution.

Proof

For the proof of this result we use the Hopf bifurcation Theorem 1. To do that, we need to prove that the hypothesis (H1) and (H2) are fulfilled.

By the definition (11) of $\mathbf {L}$, the simple purely imaginary characteristic root of the RFDE($\mathbf {L}\left( \tau \right)$) can be identify with the simple purely imaginary characteristic roots of system (6). To prove (H1) we compute the root $u=x+iy$ of the system (6 ). From the Implicit Function Theorem, there exist $\tau _{0}$ such that $0<\tau <\tau _{0}$ there exist solutions for (6). Now we obtain the purely imaginary roots $u_{0}=y_{0}i$, taking $x=0$. From the last system we obtain that $y_{0}$ has to verify the following system

$$\begin{aligned} -y^{2}\sin (y)+DK\tau y&=0,\\ -y^{2}\cos \left( y\right) +D\tau ^{2}&=0. \end{aligned}$$

Solving in $\tau$, we obtain that

$$\begin{aligned} y_{0_{\pm }}\left( \tau \right) =\pm \tau \frac{\sqrt{2}}{2}D^{1/2}\left( \sqrt{K^{4}D^{2}+4}+K^{2}D\right) ^{1/2}\ne 0,\tau >0. \end{aligned}$$

Let $u_{0_{\pm }}=y_{0_{\pm }}i$. Thus (H1) is fulfilled.

We need to check that the transversality condition (H2) holds when $x=0$. We derivate implicitly the quasi-characteristic equations (5). Let $J_{1}\left( x,y\right)$ be the real part of left hand side of (5) and $J_{2}\left( x,y\right)$ the imaginary part of left hand side of (5) denoting $w=x+iy$. Now the Eq. (5) is

$$\begin{aligned} J_{1}\left( x,y\right) +J_{2}\left( x,y\right) i=0, \end{aligned}$$

with

$$\begin{aligned} J_{1}\left( x,y\right)&=\left( x^{2}-y^{2}\right) e^{x\tau }\cos \left( y\tau \right) -2xye^{x\tau }\sin \left( y\tau \right) +DKx+D,\\ J_{2}\left( x,y\right)&=2xye^{x\tau }\cos \left( y\tau \right) +\left( x^{2}-y^{2}\right) e^{x\tau }\sin \left( y\tau \right) +DKy \end{aligned}$$

(see (6)). To obtain $x^{\prime }:=\frac{d}{d\tau }x\left( \tau \right)$ and $y^{\prime }:=\frac{d}{d\tau }y\left( \tau \right)$, we derivate the last equation:

$$\begin{aligned} \frac{\partial }{\partial x}J_{1}\left( x,y\right) x^{\prime }+\frac{\partial }{\partial y}J_{1}\left( x,y\right) y^{\prime }&=0,\\ \frac{\partial }{\partial x}J_{2}\left( x,y\right) x^{\prime }+\frac{\partial }{\partial y}J_{2}\left( x,y\right) y^{\prime }&=0. \end{aligned}$$

We are interested in nontrivial solutions for this linear system in $\left( x^{\prime },y^{\prime }\right)$. Thus, we impose the condition that the range of the matrix of system is one. So we compute the determinant of the matrix of the system

$$\begin{aligned} \Delta \left( x,y\right) =\left| \begin{array}{cc} \dfrac{\partial }{\partial x}J_{1}(x,y) &{} \dfrac{\partial }{\partial y} J_{1}(x,y) \\ \dfrac{\partial }{\partial x}J_{2}(x,y) &{} \dfrac{\partial }{\partial y} J_{2}(x,y) \end{array} \right| . \end{aligned}$$

The hypothesis of transversality (H2) is equivalent to verify that the derivative of the real part in the point (0, y) is different from zero. So, we solve $\Delta \left( 0,y\right) =0$. Calculating the partial derivatives and substituting above and computing for $x=0$, we obtain

$$\begin{aligned} \frac{\partial }{\partial x}J_{1}\left( 0,y\right)&=KD-2y\sin \left( y\tau \right) -y^{2}\tau \cos \left( y\tau \right) ,\\ \frac{\partial }{\partial y}J_{1}\left( 0,y\right)&=-2y\cos \left( y\tau \right) +y^{2}\tau \sin \left( y\tau \right) ,\\ \frac{\partial }{\partial x}J_{2}\left( 0,y\right)&=2y\cos \left( y\tau \right) -y^{2}\tau \sin \left( y\tau \right) ,\\ \frac{\partial }{\partial y}J_{2}\left( 0,y\right)&=KD-2y\sin \left( y\tau \right) -y^{2}\tau \cos \left( y\tau \right) , \end{aligned}$$

$$\begin{aligned} \Delta \left( 0,y\right)&=\left| \begin{array}{cc} KD-2y\sin \left( y\tau \right) -y^{2}\tau \cos \left( y\tau \right) &{} -2y\cos \left( y\tau \right) +y^{2}\tau \sin \left( y\tau \right) , \\ 2y\cos \left( y\tau \right) -y^{2}\tau \sin \left( y\tau \right) &{} KD-2y\sin \left( y\tau \right) -y^{2}\tau \cos \left( y\tau \right) \end{array} \right| ,\\ {\Delta \left( 0,y\right) }&\ {= \left( KD-2y\sin \left( y\tau \right) -y^{2}\tau \cos \left( y\tau \right) \right) ^2 + \left( 2y\cos \left( y\tau \right) -y^{2}\tau \sin \left( y\tau \right) \right) ^2}. \end{aligned}$$

For the values such that $\Delta$ is zero the (H2) of the Hopf conditions is fulfilled and there are changes of the structure from constant to periodic solutions according with the numerical results. To look for solutions to equation $\Delta \left( 0,y\right) = 0$, it is equivalent to look for solutions to the following nonlinear system

$$\begin{aligned} KD-2y\sin \left( y\tau \right) -y^{2}\tau \cos \left( y\tau \right)&= 0\\ 2y\cos \left( y\tau \right) -y^{2}\tau \sin \left( y\tau \right)&= 0. \end{aligned}$$

Taking in the account $z=y\tau$, and the fact that $\tau >0$ and $y\ne 0$, we can obtain numericaly that $\Delta \left( 0,0.5 {01389}\right) \approx 10^{-9}$ for $\tau =2.1 {47780}$, $K=11.389$ and $D=0.1$. For these parameters we solve numerically the problem (7)–(8) by using the code dde23 of Matlab R2018a. Additionally this procedure allows us to present graphically the appearance (see Fig. 4) of a periodic solution for the problem (7)–(8).

$\square$

Fig. 4

Delay time $\tau =2.147780.$ A stable periodic solution appears. The follower doesn’t get a constant velocity as the leader

In these phenomena we obtain a transition from a constant distance between two vehicles to another behavior which is oscillatory and this change can be noticed in the real traffic. This change of the structure, a bifurcation, is due to a delay in the action of the driver and the vehicle.

Fig. 5

Graph of the delay, time intervals and amplitudes (initial conditions given in (9))

Numericaly, we only can show the behavior of solution in ’windows’ of finite time, to perceived oscillations of numerical solution in suchs ’time windows’ (see Fig. 5). We compute, for any delay $\tau$, the mean of oscilations of numerical solution within the time intervals $[0, 20], [20, 20+20],..., [t_i, t_i+20],...,[1340, 1360]$ (from the physical point of view, we have done numerical simulations for almost four hours of car-following). We can see that for any fixed time interval (for instance the curve $(\tau , t\in [300,320], ampitude)$) the stationary solutions appear (the oscilation is zero) for small enough delay. The curve shows a typical diagram of bifurcation. The changes from constant to oscillatory behaviour are represented in the red curve at the plane (delay, time, 0). Figure 5 show that for large time, the behavior of solution for $\tau$ constant goes from oscilatory to constant behavior, for example the curve for $\tau = 1.38$ s or $\tau = 1-48$ s. Nevertheless, we have not done numerical simulation for large enouhg time in order to get the constant behavior to curve with $\tau = 1.53$ s. When the changes of the structure consist in the change of a stationary solution, as it is from a constant to a periodic solution the process we obtain a Hopf Bifurcation. This situation is obtained in Theorem 2 for $\tau = 2.147780$ s for large time.

The delay as a reaction time, mainly that of drivers, may also depends on the relative distances or velocities, that is, the state of the system. So, it would be interesting to extend this results to that case [3], although the approach to the study of periodic behaviour is somewhat different. The result obtained in this work could also be extended by looking for the solutions as a series expansion of powers of $\tau$ [6].