Thermodynamics and Reaction Mechanisms of Decomposition of the Simplest Protonated Tripeptide, Triglycine: A Guided Ion Beam and Computational Study

Abstract

We present a thorough characterization of fragmentations observed in threshold collision-induced dissociation (TCID) experiments of protonated triglycine (H⁺GGG) with Xe using a guided ion beam tandem mass spectrometer (GIBMS). Kinetic energy-dependent cross-sections for 10 ionic products are observed and analyzed to provide 0 K barriers for six primary products: [b₂]⁺, [y₁ + 2H]⁺, [b₃]⁺, CO loss, [y₂ + 2H]⁺, and [a₁]⁺; three secondary products: [a₂]⁺, [a₃]⁺, and [y₂ + 2H – CO]⁺; and two tertiary products: high energy [y₁ + 2H]⁺ and [a₂ – CO]⁺ after accounting for multiple ion-molecule collisions, internal energy of reactant ions, unimolecular decay rates, competition between channels, and sequential dissociations. Relaxed potential energy surface scans performed at the B3LYP-D3/6-311+G(d,p) level of theory are used to identify transition states (TSs) and intermediates of the six primary and one secondary products. Geometry optimizations and single point energy calculations were performed at several levels of theory. These theoretical energies are compared with experimental energies and are found to give reasonably good agreement, in particular for the M06-2X level of theory. This good agreement between experiment and theory validates the reaction mechanisms explored computationally here and elsewhere and allows identification of the product structures formed at threshold energies. The present work presents the first measurement of absolute experimental threshold energies of important sequence ions and non-sequence ions: [y₁ + 2H]⁺, [b₃]⁺, CO loss, [a₁]⁺, and [a₃]⁺, and refines those for [b₂]⁺ and [y₂ + 2H]⁺ previously measured.

Introduction

Tandem mass spectrometry (MS/MS) has been established as an important tool for studying gas-phase protonated peptide fragmentation in order to determine the amino acid sequence of peptides [1]. A typical collision-induced dissociation (CID) spectrum obtained at low collision energy is composed of multiple fragments from which the sequence of residues in a peptide can be elucidated. Effective sequencing requires rapid analysis of many CID spectra, which can be handled by automated algorithms [2–4]. A limitation of the existing sequencing algorithms is that spectra are matched against a database of possible fragments by the mass to charge ratio without considering the relative propensities for fragmentation [5]. Also, in a process like de novo sequencing where the peptide’s amino acid sequence is derived from a tandem MS/MS spectrum without the aid of a sequence database, non-sequence ions formed by losses of neutrals from primary fragments are often treated as noise by the algorithms barring some cases (e.g., peptides with serine).

Overall, limited knowledge of the underlying fragmentations may result in over-reliance on automated data interpretation, and may also prevent the critical assessment of the automated search results. Thus, sequence identification would benefit from understanding the fragmentation processes of protonated peptides, which in turn requires a thorough knowledge of the dissociation mechanisms. At present, such an understanding is incomplete even for a small peptide like triglycine made up of the “simplest” residues. Ultimately, being able to predict dissociation pathways and their probabilities will help the development of more efficient sequencing algorithms that make use of mass spectrometry data.

Gas-phase fragmentation of protonated peptides at low collision energies occurs via charge-directed mechanisms induced by migration of the proton added to the neutral peptide [5–10]. This leads to amide bond cleavage, which produces [b _n ]⁺ (containing the N-terminus) and [y _n + 2H]⁺ (containing the C-terminus) ions, known as sequence ions because they provide information on the primary structure of the peptide. The sequence [b _n ]⁺ and [y _n + 2H]⁺ ions can further dissociate to give smaller [b _m ]⁺ ions, [y _m + 2H]⁺, and [a _n ]⁺ ions, internal fragments, or immonium ions. Non-sequence product ions are formed by the loss of small neutral molecules like water, carbon monoxide, and ammonia. The nomenclature used for peptide fragment ions in this study is adopted from the “all-explicit” nomenclature proposed by Siu and co-workers [11], a modification of that proposed by Roepstorff and Fohlmann [12], and Biemann [13].

The system of interest here, protonated triglycine, H⁺GGG, is one of the most extensively studied model peptides. The earliest quantitative experimental study on the decomposition of H⁺GGG was done by Klassen and Kebarle (KK) [14], who measured the CID of small protonated molecules and peptides as a function of kinetic energy in a triple quadrupole mass spectrometer. Reid, Simpson, and O’Hair [15] reexamined this system and performed MS/MS experiments that were not kinetic energy-resolved. In both studies, possible mechanisms for product formation were suggested, but no detailed mechanisms were explicitly developed for the H⁺GGG system. Aribi et al. updated these results by investigating the fragmentations of H⁺GGG experimentally using threshold collision-induced dissociation (TCID) and extracting threshold energies for three processes from energy-resolved CID spectra [16]. They also used density functional theory (DFT) at the B3LYP/6-31++G(d,p) level to elucidate the fragmentation mechanisms, building on previous computational work by Rodriquez et al. (RCSCHS), who had explored the “proton migration and tautomerism” in H⁺GGG [17]. Studies undertaken by Paizs and Suhai (PS) took a close theoretical look at the H⁺GGG system, albeit with a relatively small basis set, B3LYP/6-31G(d) [18, 19]. They identified key conformers (intermediates) formed as a result of protonation at different sites and the transition states (TSs) connecting the intermediates involved in the cis-trans isomerization of the peptide bond. By calculating unimolecular rate constants for TSs using Rice-Ramsperger-Kassel-Marcus (RRKM) theory [20, 21], the authors concluded that cis-trans isomerization of the N-terminal peptide bond in H⁺GGG is energetically feasible but is a time-consuming process. Such cis-trans isomerization is crucial only if [y₁ + 2H]⁺ ions are formed via the “diketopiperazine” (DKP) pathway. PS also investigated the mechanisms for fragmentation of H⁺GGG to [b₂]⁺ and [y₁ + 2H]⁺ ions via both the oxazolone and DKP pathways [19]. Although formation of [y₁ + 2H]⁺ was found to be loose (limited by product energies) along the oxazolone pathway, the DKP pathway was found to be limited by a tight TS (TTS). The DKP pathway is inconsistent with the experimental results obtained by Morgan and Bursey [22], who saw a linear correlation between the relative intensities of [y₁ + 2H]⁺ and [b₂]⁺ and the proton affinities of the C-terminal amino acid residue (glycine in this case), suggesting that [b₂]⁺ and [y₁ + 2H]⁺ products share common pathways. Likewise, Wesdemiotis and co-workers [23] observed a very small kinetic energy release for formation of [y₁ + 2H]⁺ ions, consistent with a loose TS. Fragmentation of C-terminally amidated H⁺GGG, H⁺GGGNH₂, was recently examined experimentally by MS/MS, infrared multiple photon dissociation (IRMPD), and chemical dynamics simulations [24]. Detailed reaction mechanisms were not characterized, although possible pathways were suggested.

The present study extends these previous works by providing a more comprehensive examination of the reaction mechanisms, detailed quantitative data, and much more in-depth analyses of the data, thereby providing more extensive and quantitative energetic information. Here, we measure absolute cross-sections of the observed TCID reactions with a sensitivity of nearly three orders of magnitude using a guided ion beam tandem mass spectrometer (GIBMS). An important result of this study is the assortment of sequence and non-sequence ions that are obtained as products from H⁺GGG fragmentation (seven more than previously identified). These experimental results are analyzed using molecular parameters (vibrational frequencies and rotational constants) determined in theoretical calculations to extract absolute experimental threshold energies of each fragmentation pathway. The experimental threshold energies are compared with those obtained from single point energy calculations performed at the B3LYP, B3LYP-D3 (B3LYP with the GD3BJ dispersion correction [25, 26]), MP2(full), and M06-2X levels of theory. Agreement between the experimental and theoretical energies verifies that the key steps involved in H⁺GGG fragmentation have been properly identified and supports the mobile proton model [6, 8–10, 27], which allows an understanding of peptide dissociation chemistry. The present analysis of the kinetic energy-dependent cross-sections of H⁺GGG fragmentations provides the first complete experimental determination of the threshold energies of sequence and non-sequence ions formed from decomposition of any tripeptide.

Experimental and Computational Details

Experimental Procedures

Cross-sections of H⁺GGG colliding with Xe are measured using a GIBMS that has been described previously in detail [28, 29]. The H⁺GGG ions were generated using an electrospray ionization source (ESI) [30] under conditions similar to those described earlier, such that the H⁺GGG ions are characterized by a temperature of 300 K [31–36]. Details of the experimental methods and means of data analysis can be found in the Supporting Information (SI). All energies reported here are in the center-of-mass (CM) frame unless otherwise noted.

Computational Details

Model structures and vibrational frequencies of reactants, products, TSs, and intermediates were obtained at B3LYP/6-311+G(d,p) and B3LYP-D3/6-311+G(d,p) levels of theory. Single-point energies corrected for zero-point energies were calculated at B3LYP, B3LYP-D3, and MP2(full) (where full refers to correlation of all electrons, simply referred to as MP2 below) levels of theory using the 6-311+G(2d,2p) basis set. Details of these procedures can be found in the SI. Geometries of key H⁺GGG conformers, TSs, and products were also optimized at M06-2X/6-311+G(d,p) with single-point energies calculated at B3LYP, MP2, and M06-2X levels of theory. In the following, basis sets are not explicitly given as they always correspond to L1/6-311+G(2d,2p)//L2/6-311+G(d,p), where L1 refers to the level of theory for single-point energies and L2 for geometry optimizations. Single-point energies determined at the B3LYP and MP2 levels using 6-311+G(2d,2p) basis sets compared accurately with experimental energies (with mean absolute deviations of about 10 kJ/mol) in studies of protonated glycine (H⁺G) [37], diglycine (H⁺GG) [38, 39], [b₂]⁺ (H⁺AMOx), and diketopiperazine (H⁺DKP) [40] and also illustrate the range of energies that can be obtained computationally.

Nomenclature

Conformers of the H⁺GGG reactant are named using a nomenclature that identifies the site of protonation within square brackets, followed by designation of eight dihedral angles starting from the N terminus and going along the backbone of H⁺GGG to the hydroxyl group: ∠N¹CCN², ∠CCN²C, ∠CN²CC, ∠N²CCN³, ∠CCN³C, ∠CN³CC, ∠N³CCO⁴, ∠CCO⁴H, where the superscripts 1, 2, 3 denote the first, second, and third glycine residue, and superscript 4 indicates the hydroxyl oxygen, the point where the fourth peptide bond would form. The dihedral angles are labeled as c (cis) for angles <45°, g (gauche) for angles between 45° and 135°, and t (trans) for angles >135°. Thus the B3LYP ground structure (GS) is named [O^1t]-ctgttttt, where the site of protonation is the carbonyl oxygen of the first glycine residue, and the superscript t denotes the orientation of the proton by specifying that ∠CCO¹H is trans. When the lone pair on the N-terminal amino group is trans to the C–C bond, ∠N¹CCN² is denoted by a superscript t. In some cases, we assign subscripts + and – for gauche and trans dihedral angles having opposite signs and leading to distinct conformations. Product conformers are named in a similar manner, defining the protonation site and the relevant dihedral angles.

Transition states are indicated by TS followed by a description of the change in the protonation site, dihedral angle, or bond cleavage. Thus, the TS for a proton transfer is named TS[O¹-N²] indicating transfer of a proton from the carbonyl oxygen O¹ (the lower energy conformer) to the amide nitrogen N². A TS involving a dihedral angle change is designated within parentheses, e.g., (cg), which indicates that the dihedral angle changes from cis (the lower energy conformer) to gauche. A TS involving cleavage of a bond indicates the bond broken by ~ inside curly brackets, e.g., {OC~N²}. Although more complicated than simply numbering species, this nomenclature has proven to be useful in distinguishing conformations, while depicting connections between intermediates, and allows better visualization of the change taking place [37, 39–41].

Energies for all species are given in terms of the range of values obtained computationally from the single point energy calculations corrected for zero point energies at the B3LYP, B3LYP-D3, MP2, and M06-2X levels of theory relative to their respective GSs (i.e., [O^1t]-ctgttttt for DFT and [N¹]-ttggtgtt for MP2), as discussed in the SI. Complete tables of all computed values can be found in SI: Supplementary Tables S1 for H⁺GGG conformers, S3 for GGG conformers, S4 for intermediates, and S5 for TSs.

Results

Cross-Sections for Collision-Induced Dissociation

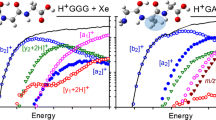
Figure 1 shows the experimental kinetic energy-dependent cross-sections obtained for the interaction of H⁺GGG with Xe. Ten ionic products are observed for H⁺GGG (m/z 190) fragmentation. On the basis of the theoretical results, these are assigned to reactions 1a–10.

Figure 1

Cross-sections for collision-induced dissociation of H⁺GGG with xenon at 0.2 mTorr as a function of kinetic energy in the center-of-mass (CM) frame in the lower x-axis and in the laboratory frame (Lab) in the upper x-axis. Products are identified by their mass to charge ratio and the all explicit nomenclature for fragment ions. Open symbols show the primary products and closed symbols show the products formed by sequential dissociation. The solid line shows the total cross-section

$$ {\mathrm{H}}^{+}\mathrm{G}\mathrm{G}\mathrm{G}+\mathrm{X}\mathrm{e}\to {\mathrm{C}}_4{\mathrm{H}}_7{\mathrm{N}}_2{{\mathrm{O}}_2}^{+}\left({\left[{\mathrm{b}}_2\right]}^{+}\right)+{\mathrm{C}}_2{\mathrm{H}}_5{\mathrm{N}\mathrm{O}}_2+\mathrm{X}\mathrm{e} $$

(1a)

$$ \to {\mathrm{C}}_4{\mathrm{H}}_7{\mathrm{N}}_2{{\mathrm{O}}_2}^{+}\left({\left[{\mathrm{b}}_2\right]}^{+}\right) + \mathrm{C}\mathrm{O} + {\mathrm{C}\mathrm{H}}_2\mathrm{N}\mathrm{H} + {\mathrm{H}}_2\mathrm{O} + \mathrm{X}\mathrm{e} $$

(1b)

$$ \to {\mathrm{C}}_2{\mathrm{H}}_6{{\mathrm{N}\mathrm{O}}_2}^{+}\left({\left[{\mathrm{y}}_1 + 2\mathrm{H}\right]}^{+},\ {\mathrm{H}}^{+}\mathrm{G}\right) + {\mathrm{C}}_4{\mathrm{H}}_6{\mathrm{N}}_2{\mathrm{O}}_2 + \mathrm{X}\mathrm{e} $$

(2a)

$$ \to {\mathrm{C}}_2{\mathrm{H}}_6{{\mathrm{NO}}_2}^{+}\left({\left[{\mathrm{y}}_1 + 2\mathrm{H}\right]}^{+},\ {\mathrm{H}}^{+}\mathrm{G}\right) + 2\ \mathrm{C}\mathrm{O} + 2\ {\mathrm{C}\mathrm{H}}_2\mathrm{N}\mathrm{H} + \mathrm{X}\mathrm{e} $$

(2b)

$$ \to {\mathrm{C}}_6{\mathrm{H}}_{10}{\mathrm{N}}_3{{\mathrm{O}}_3}^{+}\left({\left[{\mathrm{b}}_3\right]}^{+}\right) + {\mathrm{H}}_2\mathrm{O} + \mathrm{X}\mathrm{e} $$

(3)

$$ \to {\mathrm{C}}_5{\mathrm{H}}_9{\mathrm{N}}_2{{\mathrm{O}}_3}^{+} + \mathrm{C}\mathrm{O} + {\mathrm{N}\mathrm{H}}_3 + \mathrm{X}\mathrm{e} $$

(4)

$$ \to {\mathrm{C}}_4{\mathrm{H}}_9{\mathrm{N}}_2{{\mathrm{O}}_3}^{+}\left({\left[{\mathrm{y}}_2 + 2\mathrm{H}\right]}^{+},\ {\mathrm{H}}^{+}\mathrm{GG}\right) + \mathrm{C}\mathrm{O} + {\mathrm{C}\mathrm{H}}_2\mathrm{N}\mathrm{H} + \mathrm{X}\mathrm{e} $$

(5)

$$ \to {\mathrm{C}}_5{\mathrm{H}}_{10}{\mathrm{N}}_3{{\mathrm{O}}_2}^{+}\left({\left[{\mathrm{a}}_3\right]}^{+}\right) + {\mathrm{H}}_2\mathrm{O} + \mathrm{C}\mathrm{O} + \mathrm{X}\mathrm{e} $$

(6)

$$ \to {\mathrm{C}\mathrm{H}}_2{{\mathrm{N}\mathrm{H}}_2}^{+}\left({\left[{\mathrm{a}}_1\right]}^{+}\right) + \mathrm{C}\mathrm{O} + {\mathrm{C}}_4{\mathrm{H}}_8{\mathrm{N}}_2{\mathrm{O}}_3 + \mathrm{X}\mathrm{e} $$

(7a)

$$ \to {\mathrm{C}\mathrm{H}}_2{{\mathrm{N}\mathrm{H}}_2}^{+}\left({\left[{\mathrm{a}}_1\right]}^{+}\right) + {\mathrm{C}}_4{\mathrm{H}}_6{\mathrm{N}}_2{\mathrm{O}}_2 + \mathrm{C}\mathrm{O} + {\mathrm{H}}_2\mathrm{O} + \mathrm{X}\mathrm{e} $$

(7b)

$$ \to {\mathrm{C}\mathrm{H}}_2{{\mathrm{NH}}_2}^{+}\left({\left[{\mathrm{a}}_1\right]}^{+}\right) + {\mathrm{C}\mathrm{H}}_2\mathrm{N}\mathrm{H} + 2\ \mathrm{C}\mathrm{O} + {\mathrm{C}}_2{\mathrm{H}}_5{\mathrm{NO}}_2 + \mathrm{X}\mathrm{e} $$

(7c)

$$ \to {\mathrm{CH}}_2{{\mathrm{NH}}_2}^{+}\left({\left[{\mathrm{a}}_1\right]}^{+}\right) + 3\ \mathrm{C}\mathrm{O} + 2\ {\mathrm{CH}}_2\mathrm{N}\mathrm{H} + {\mathrm{H}}_2\mathrm{O} + \mathrm{X}\mathrm{e} $$

(7d)

$$ \to {\mathrm{C}}_3{\mathrm{H}}_7{\mathrm{N}}_2{\mathrm{O}}^{+}\left({\left[{\mathrm{a}}_2\right]}^{+}\right) + \mathrm{C}\mathrm{O} + {\mathrm{C}}_2{\mathrm{H}}_5{\mathrm{N}\mathrm{O}}_2 + \mathrm{X}\mathrm{e} $$

(8a)

$$ \to {\mathrm{C}}_3{\mathrm{H}}_7{\mathrm{N}}_2{\mathrm{O}}^{+}\left({\left[{\mathrm{a}}_2\right]}^{+}\right) + 2\ \mathrm{C}\mathrm{O} + {\mathrm{C}\mathrm{H}}_2\mathrm{N}\mathrm{H} + {\mathrm{H}}_2\mathrm{O} + \mathrm{X}\mathrm{e} $$

(8b)

$$ \to {\mathrm{C}}_3{\mathrm{H}}_9{\mathrm{N}}_2{{\mathrm{O}}_2}^{+}\left({\left[{\mathrm{y}}_2 + 2\mathrm{H}\ \hbox{--}\ \mathrm{CO}\right]}^{+}\right) + 2\ \mathrm{C}\mathrm{O} + {\mathrm{C}\mathrm{H}}_2\mathrm{N}\mathrm{H} + \mathrm{X}\mathrm{e} $$

(9)

$$ \to {\mathrm{C}}_2{\mathrm{H}}_7{{\mathrm{N}}_2}^{+}\left({\left[{\mathrm{a}}_2\hbox{-}\ \mathrm{CO}\right]}^{+}\right) + 2\ \mathrm{C}\mathrm{O} + {\mathrm{C}}_2{\mathrm{H}}_5{\mathrm{N}\mathrm{O}}_2+\mathrm{X}\mathrm{e} $$

(10)

Importantly, Figure 1 shows that the total cross-section increases smoothly with increasing energy, consistent with the sequential nature of the coupled reactions 1a–10 as outlined in the following.

The lowest energy process arises from the loss of neutral glycine to form the [b₂]⁺ ion (m/z 115) in reaction 1a. Previous work in our laboratory and others has identified this species as protonated 2-aminomethyl-5-oxazolone (H⁺AMOx) [16, 19, 40, 42–47] as originally suggested by Harrison and co-workers [48]. The next largest cross-section is associated with formation of [y₂ + 2H]⁺ (m/z 133, protonated diglycine, H⁺GG) in reaction 5. At slightly lower energies than [y₂ + 2H]⁺ formation, the [y₁ + 2H]⁺ ion (m/z 76, protonated glycine, H⁺G) is formed in reaction 2a, which directly competes with reaction 1a because both channels differ only in which fragment keeps the extra proton. After rising to about 0.5 Ų, the [y₁ + 2H]⁺ cross-section rises again near 4 eV, indicating the contribution of a new pathway to this product, reaction 2b. Formation of the [b₃]⁺ ion (m/z 172) has a similar apparent threshold as [y₂ + 2H]⁺ and corresponds to loss of water from H⁺GGG to form protonated 2-glycylaminomethyl-5-oxazolone (H⁺GAMOx) in reaction 3. A similar threshold is also found for the m/z 145 product ion formed in reaction 4 by the combined losses of CO + NH₃. Although both reactions 4 and 5 include the loss of CO, no primary ion at the appropriate mass (m/z 162) was observed, despite carefully looking for it. This can occur if CO loss involves a TTS such that loss of additional fragments from m/z 162 can occur readily at the energy of the TTS. This result is also consistent with similar low-energy and millisecond timescale ion trap/CID experiments of Bythell et al. for fragmentation of H⁺AGG [49]; however, they did observe the loss of CO in MALDI/TOF-TOF, metastable ion (MI), and CID experiments occurring at microsecond timescales and higher energies. The next product observed here is formed in reaction 6, where CO is lost from the [b₃]⁺ ion to form [a₃]⁺ (m/z 144). Formation of [a₁]⁺ (m/z 30) in reaction 7 has a similar apparent threshold as [a₃]⁺ but is clearly much more efficient, dominating the products seen at high energies. This can be attributed to the multiple pathways that are capable of yielding [a₁]⁺ adding to its overall product intensity, discussed below. At about the same apparent threshold as [a₁]⁺, formation of [a₂]⁺ (m/z 87) in reaction 8 is observed, and corresponds to loss of CO from [b₂]⁺. Two minor products, [y₂ + 2H – CO]⁺ (m/z 105) and [a₂ – CO]⁺ (m/z 59, H⁺(CH₂NH₂)₂) are observed at higher energies and correspond to decarbonylation of [y₂ + 2H]⁺ in reaction 9 and [a₂]⁺ in reaction 10.

Cross-sections of five of the six primary products ([b₂]⁺, [y₂ + 2H]⁺, [y₁ + 2H]⁺, [b₃]⁺, and –[CO + NH₃]) start to decline after an initial rise to a maximum cross-section. The [b₂]⁺ ion in reaction 1a can lose CO to form [a₂]⁺, studied previously in our laboratory and by others [14, 16, 40, 43–46, 48, 50–55]. This is consistent with the decline of [b₂]⁺ and rise of [a₂]⁺ at about 3 eV, Figure 1. The [a₂]⁺ cross-section declines at higher energies because it decomposes by additional CO loss to form m/z 59 ([a₂ – CO]⁺), which then dissociates to [a₁]⁺ in reaction 7c, as shown previously [40, 56]. The decline in the [y₂ + 2H]⁺ (H⁺GG) cross-section at higher energies is associated with loss of H₂O to form [b₂]⁺, reaction 1b, and with loss of CO, reaction 9, as shown in previous work [38]. The [y₂ + 2H – CO]⁺ (m/z 105) product ion rapidly dissociates to [y₁ + 2H]⁺ (H⁺G) by reaction 2b, which accounts for the second feature in the [y₁ + 2H]⁺ cross-section starting at ~4 eV. These relative energetics are consistent with a study of H⁺GG (here the [y₂ + 2H]⁺ product ion) decomposition where formation of m/z 76 begins at ~1.4 eV (which should be added to the threshold for [y₂ + 2H]⁺ formation) [38]. The primary [y₁ + 2H]⁺ product cross-section declines above 3 eV because it can dissociate by loss of CO + H₂O to form [a₁]⁺ in reaction 7b, consistent with direct studies of the decomposition of H⁺G [37]. The [b₃]⁺ primary product dissociates by CO loss to form [a₃]⁺ in reaction 6, consistent with the shapes and magnitudes of these two cross-sections. The [a₃]⁺ product can dissociate further to lose CH₂NH forming the [b₂]⁺ ion (reaction 1b), a process that has been examined and documented in the past [51, 57, 58], or lose AMOx to form [a₁]⁺ ions in reaction 7b. Neither of these pathways is evident in the [b₂]⁺ and [a₁]⁺ cross-sections as these products are also formed via other more probable routes. The m/z 145 product ion formed by loss of CO + NH₃ must also dissociate at higher energies, but because the magnitude of its cross-section is relatively low, no subsequent product channels can be assigned definitively.

Note that there are five pathways leading to formation of [a₁]⁺ (CH₂NH₂ ⁺): a primary decarbonylation of H⁺GGG (7a) competitive with reaction 5, a secondary product formed via [y₁ + 2H]⁺ (7b), a quaternary product formed via [b₂]⁺ and [a₂]⁺ (7c), a tertiary product formed via [y₂ + 2H]⁺ (7c), and a quaternary product formed via [y₂ + 2H]⁺ and [y₁ + 2H]⁺ (7d) [37, 38, 40]. A sixth potential process in which the [b₂]⁺ ion decomposes directly to form [a₁]⁺ along with C₃H₃NO₂, originally proposed by Siu and co-workers [52], was found to be unimportant in our previous analysis of the [b₂]⁺ ion decomposition [40]. Further support for this conclusion comes from a recent study that examined the direct fragmentation of [b₂]⁺ to [a₁]⁺ for a series of protonated tripeptides and concluded that this dissociation is insignificant for [b₂]⁺ ions with a glycylglycine sequence [59]. Notably, the magnitude of the [a₂ – CO]⁺, H⁺(CH₂NH)₂, product cross-section in the current and previous studies [40] are comparable, ~0.4 Ų at about 8 eV in the CM frame, although these cross-sections have slightly different shapes, which can be attributed to the different energy dependences of their precursor [a₂]⁺ ion.

As mentioned above, the decomposition of H⁺GGG as a function of kinetic energy has been investigated previously by KK in a triple quadrupole mass spectrometer [14]. They observed the ionic products: [b₂]⁺, [y₁ + 2H]⁺, [y₂ + 2H]⁺, [a₁]⁺, and [a₂]⁺, the dominant products observed in the current results (those with cross-sections exceeding 1 Ų). Similar to our results, [b₂]⁺ was found to be the energetically favored process, with [y₂ + 2H]⁺ next, [y₁ + 2H]⁺ showed bimodal behavior, and [a₁]⁺ was the dominant product at high energies. Relative intensities of [y₂ + 2H]⁺, [y₁ + 2H]⁺, [a₁]⁺, and [a₂]⁺ are similar to those observed here, but KK’s data differ mainly in the relative [b₂]⁺ intensity, which is smaller than observed here, and in a pronounced low energy tail to the [a₁]⁺ cross-section. In their MS/MS spectra of H⁺GGG, Reid et al. observed the formation of [b₂]⁺, [b₃]⁺, [y₁ + 2H]⁺, combined loss of CO + NH₃, and [a₂]⁺ products with the [b₂]⁺ product ion being the most intense [15]. No energy-resolved data were acquired. Aribi et al. [16] examined the kinetic energy dependence of H⁺GGG fragmentation to form [b₂]⁺ followed by its decarbonylation to [a₂]⁺, and formation of [a₁]⁺ ions from both [b₂]⁺ and [a₂]⁺. (None of the other products observed here were included and only the [b₂]⁺ cross-section was shown.) These cross-sections were analyzed to obtain experimental thresholds.

H⁺GGG Ground Structure

B3LYP//B3LYP, B3LYP-D3//B3LYP-D3, B3LYP//M06-2X, and M06-2X//M06-2X calculations suggest that protonation occurs most favorably at the carbonyl oxygen O¹ of H⁺GGG, Figure 2. Thus, these levels of theory indicate [O^1t]-ctgttttt is the ground structure (GS), in concert with the B3LYP results of PS (for their O2_TT_1) [18, 19] and Wu and McMahon (WM) (for their GGGH01) [60]. In this conformer, the proton on O¹ interacts with the carbonyl oxygen of the second glycine residue, leading to a stabilizing O¹H•O² hydrogen bond of 1.42 Å. RCSCHS [17] found that the [O^1c]-tttttgtt conformer is the GS, which is calculated here to be 16–20 kJ/mol above [O^1t]-ctgttttt, Supplementary Table S1.

Figure 2

H⁺GGG conformers, [O^1t]-ctgttttt, [N¹]-gcgttgtt, [N¹]-ttggtgtt, and [N¹]-tcgctgtt with their relative energies at B3LYP//B3LYP, B3LYP-D3//B3LYP-D3, M06-2X//M06-2X, and MP2//B3LYP levels of theory

Figure 3

Competitive modeling of the six primary products: composite cross-sections of [b₂]⁺ _tot, [y₂ + 2H]⁺ _tot, [y₁ + 2H]⁺ _LE, [b₃]⁺, loss of (CO + NH₃), and [a₁]⁺ from H⁺GGG. Symbols show zero-pressure extrapolated data for the indicated process between H⁺GGG and Xe as a function of collision energy in the center-of-mass frame (lower x-axis) and in the laboratory frame (upper x-axis). Solid lines show the best fit to the data using the model in Equation S1 convoluted over the neutral and ion kinetic and internal energy distributions. Dashed lines show the model cross-sections in the absence of experimental kinetic energy broadening for reactants with internal energies at 0 K

Figure 4

Sequential modeling of the [a₃]⁺ ion formed by CO loss from [b₃]⁺ along with competitive modeling of the remaining primary ions. The [y₁ + 2H]⁺ _LE and loss of CO + NH₃ products are not shown for purposes of clarity. Symbols show high-pressure data for the indicated process between H⁺GGG and Xe as a function of collision energy in the center-of-mass frame (lower x-axis) and in the laboratory frame (upper x-axis). Solid lines show the best fit to the data using the models in Equations S1, S3a, and S3b convoluted over the neutral and ion kinetic and internal energy distributions. Dashed lines show the model cross-sections in the absence of experimental kinetic energy broadening for reactants with internal energies at 0 K

Figure 5

Comparison of experimental threshold energies for the products shown modeled using Equations S1 and S3 with B3LYP (red triangles), B3LYP-D3 (green triangles), MP2 (blue circles), and M06-2X (purple squares) energies taken from Table 1. The diagonal line indicates perfect agreement between theory and experiment

In contrast, calculations done at MP2//B3LYP and MP2//M06-2X find N¹ is the most favorable site for protonation, suggesting that [N¹]-gcgttgtt (called 2a′ by Wu and Lebrilla [61], P1 by RCSCHS, and N1_CT_1 by PS) is the lowest energy species, with [O^1t]-ctgttttt being 2–6 kJ/mol higher, Supplementary Table S1. We also located two more [N¹] conformers with similar energies: [N¹]-ttggtgtt (2 by Zhang et al. [62, 63], 1 by RCSCHS, N1_TT_1 by PS, GGGH02 by WM), and [N¹]-tcgctgtt (2a′′ by Wu and Lebrilla, N1_CT_2 by PS). Both [N¹]-gcgttgtt and [N¹]-tcgctgtt conformers are characterized by a cis N-terminal peptide bond (second dihedral angle), hence the CT designation of PS, whereas [O^1t]-ctgttttt and [N¹]-ttggtgtt have trans N-terminal peptide bonds. For overlapping species and levels of theory, our results for these species are comparable to the calculations of WM, PS, and RCSCHS, Supplementary Table S1; however, only PS considered all four of these conformers.

WM found that a combination spectrum of their lowest energy isomers, [O^1t]-ctgttttt and [N¹]-ttggtgtt, compared well with their experimentally obtained IRMPD spectrum, thus concluding that both species are present in their experiments. Here, we find that both [N¹]-gcgttgtt and [N¹]-tcgctgtt are lower in energy than [N¹]-ttggtgtt at all levels of theory, and neither was considered by WM. The predicted spectra for these four conformers are compared with the experimental IRMPD spectrum of WM in Supplementary Figure S2. The discussion in the SI suggests that [O^1t]-ctgttttt and [N¹]-ttggtgtt are indeed the dominant species, in agreement with WM’s conclusions. The two lower energy [N¹] conformers are either not present or have low abundance. These results indicate that B3LYP relative energies for the [O¹] and [N¹] conformers are likely to be inaccurate, and either the B3LYP-D3, MP2, and M06-2X relative energies are also flawed or the two low-energy [N¹] isomers having a cis N-terminal peptide bond are inaccessible to an ESI source. The latter hypothesis is explored more fully in the SI, where we conclude that the cis species are probably not formed in solution or in the ESI source because the neutral GGG molecule does not have ready access to the cis peptide bond conformers. Additionally, the rate-limiting TS for cis-trans isomerization in the protonated molecule, TS[N¹]-g(ct)gttttt, lies 61–80 kJ/mol above the GS (Supplementary Figure S4 and Supplementary Table S5), which is high enough to prevent the cis-trans isomerization from occurring in solution or an ESI source. As a consequence, Figure 2 and Supplementary Tables S1, S4, and S5 list MP2 energies of all species relative to the [N¹]-ttggtgtt isomer and M06-2X energies relative to [O^1t]-ctgttttt, as these are the lowest energy conformer according to each of these levels that is accessible experimentally. For B3LYP and B3LYP-D3, energies are listed relative to their [O^1t]-ctgttttt ground structure.

In analogy to this work, both [N¹] and [O¹] structures were found in the IRMPD study of H⁺GGGNH₂ [24]. The N-terminal protonated H⁺GGGNH₂ was calculated to be the lowest energy H⁺GGGNH₂ at DFT levels of theory. Although the authors identified two [N¹] structures with folded conformations as major contributors to the experimental spectra of H⁺GGGNH₂, an [O¹] structure with a linear backbone (similar to [O^1t]-ctgttttt) was required to account for some features of their IRMPD spectra.

Additionally, Wyttenbach, Bushnell, and Bowers [64, 65] measured experimental collision cross-sections (CCS) of protonated Gly_n (n = 1−6) oligopeptides, with their values for n = 1–3 listed in Supplementary Table S2. Their ion mobility experiments used a matrix laser desorption ionization (MALDI) source and were conducted at 300 and 80 K (where the resolution at the colder temperature is twice that at room temperature). The experimental CCS measurements found no evidence of multiple structures for any of the systems, which is expected for the smaller H⁺G and H⁺GG systems, but is inconsistent with the IRMPD studies for H⁺GGG. This disparity can be attributed to the use of different ion sources for the two sets of experiments. As discussed in detail in the SI, the CCSs can be compared with those computed by two different programs [65, 66]. Good agreement between experiment and theory for H⁺G and H⁺GG is found, but not for the H⁺GGG system, such that an unequivocal assessment of which conformer is present cannot be made. However, the low-energy [N¹] structures located here are most consistent with the experimental CCS results as discussed in detail in the SI, which would suggest that MP2 theory provides the most reliable relative energetics.

Given that both [N¹]-ttggtgtt and [O^1t]-ctgttttt isomers of H⁺GGG appear to be present in the results of WM, we have explored the pathway connecting these low-energy isomers, described in detail in SI, Supplementary Figure S5. Overall, the rate-limiting TS connecting the [N¹]-ttggtgtt and [O^1t]-ctgttttt isomers is TS[O^1c]-(tc)tgttttt, which lies 77–82 kJ/mol above the GS. Such energies are probably inaccessible in an ESI source such that interconversion of [O^1t]-ctgttttt and [N¹]-ttggtgtt are unlikely, and thus must be formed independently in the source. However, this TS energy is sufficiently low that interconversion of these isomers is energetically possible in the TCID experiments, as this energy is well below the thresholds for the decomposition reactions discussed below, ≥171 ± 6 kJ/mol.

[b₂]⁺/[y₁ + 2H]⁺ Formation

The reaction mechanism for the formation of [b₂]⁺ and [y₁ + 2H]⁺ ions has been studied previously [17, 19, 49]. At a higher level of theory, we reproduce the pathway found by PS, as shown in Supplementary Figure S6 starting from [O^1t]-ctgttttt, the DFT GS. As noted above, rearrangement of this species to the MP2 GS, [N¹]-ttggtgtt, is possible upon activation such that the rate-limiting TS (in all mechanisms explored here) is the same for both isomers. Overall, formation of the [b₂]⁺ and [y₁ + 2H]⁺ product ions is limited by the energies of the separated products (i.e., they have loose TSs). This conclusion is consistent with the large cross-sections observed for these two products in Figure 1. Formation of [b₂]⁺ + G is calculated to lie 153–172 (170 by PS) kJ/mol above the GS and that of [y₁ + 2H]⁺ (H⁺G) + AMOx is 182–200 (188 by PS) kJ/mol above the GS, and 20–30 kJ/mol above [b₂]⁺ + G. RCSCHS reported a pathway for the formation of the [b₂]⁺ ion with a rate-limiting TS above the pathway elucidated here by ~30 kJ/mol. Importantly, RCSCHS used relative free energies to assess the rate-limiting steps; however, comparison of relative enthalpies is needed for TCID measurements, which determines bond enthalpies at 0 K. Entropy cannot be used to overcome barriers; it only determines the relative probability of the process (i.e., the Arrhenius pre-exponential factor in the rate coefficient).

[y₂ + 2H]⁺/[a₁]⁺ Formation

Formation of the [y₂ + 2H]⁺ and [a₁]⁺ product ions from H⁺GGG has been examined in the past [14, 19]. Here we have reexamined these mechanisms at higher levels of theory and report the entire mechanism in SI, Supplementary Figure S8. Briefly the formation of [y₂ + 2H]⁺ and [a₁]⁺ product ions must involve transfer of the mobile proton to the N² amide nitrogen and the subsequent loss of CO. We find that the rate-limiting TS, TS[N²]-t_ttgttttt{N¹C~CO¹~N²C} for the decarbonylation reaction lies 164–175 kJ/mol above the GS and leads to the formation of complexes of CH₂NH₂ ⁺, GG, and CO (eight variants were found), which lie 62–95 kJ/mol below the TS and 77–102 kJ/mol above the GS, Supplementary Tables S4 and S5. In addition to this pathway, we found another two pathways with similar rate-limiting TSs that lie 2–7 kJ/mol higher in energy, Supplementary Table S5. One of these reproduces the pathway and rate-limiting TS of PS, TS[N²]-cggttttt{N¹C~CO¹~N²C} (Y2_A1Y1_TS), and the third pathway occurs via rate-limiting TS[N²]-ctgttttt{N¹C~CO¹~N²C}. These three TSs differ from each other only in the spatial arrangement of the incipient immonium ion; however, TS[N²]-t_ttgttttt{N¹C~CO¹~N²C} is less constrained than the other two TSs, which means it should dominate the observed reaction as it is entropically and slightly enthalpically favored. The TSs presented here are analogous forms of the TS[N²]-cggtt{C^α1~OC~N²} obtained for loss of CO from H⁺GG found by Armentrout and Heaton [39] and from H⁺AGG by Bythell et. al [49]. Additionally, we tried to locate a pathway that does not involve sequential losses of CO and CH₂NH or GG to form [y₂ + 2H]⁺ and [a₁]⁺ ions, but were unable to do so.

Once over one of the rate-limiting TS[N²]{N¹C~CO¹~N²C}, several complexes of the CH₂NH₂ ⁺ ion bound to diglycine and CO can be formed. We located nine of these, including one reported by PS, as detailed in the SI. Similarly, once CO is lost, the (CH₂NH)H⁺(GG) complexes can explore different conformations (six were located, including two found by PS, as detailed in the SI). The various CH₂NH(H⁺)GG + CO isomers are well below the three TS[N²]{N¹C~O¹C~CN²} rate-limiting TSs, Supplementary Tables S4 and S5. Any of these CH₂NH(H⁺)GG species can dissociate to form either the [y₂ + 2H]⁺ (H⁺GG) + CH₂NH or [a₁]⁺ (CH₂NH₂ ⁺) + GG products at higher energies. These subsequent dissociations are limited by the separated product energies, consistent with the large cross-sections observed for these channels, Figure 1. Formation of [y₂ + 2H]⁺ + CH₂NH + CO is calculated to lie 1–36 kJ/mol above the rate-limiting TSs, and [a₁]⁺ + GG + CO lies 62–94 kJ/mol above the rate-limiting TSs (52–67 kJ/mol above the competing [y₂ + 2H]⁺ channel). Dissociation to yield [y₂ + 2H]⁺ and [a₁]⁺ ions is a competitive process because the proton is shared between the two molecules at their favored protonation sites.

PS also examined the pathway yielding a three-membered ring aziridinone product, c-CH₂NHCO [19], originally postulated by Cordero et al. [67] and suggested for H⁺GGG by KK [14] and explored for dipeptides by PS [5]. This pathway was found to be limited by TSs that exceed those outlined here by ~40 kJ/mol, in agreement with the conclusions of PS. Thus the aziridinone pathway was not explored here.

[b₃]⁺ Formation (Loss of Water from H⁺GGG)

Mechanisms for the loss of water from H⁺GGG have been previously explored by O’Hair et al. [68] and Reid et al. [15]. These studies demonstrated that water loss occurred from the C-terminus and resulted in an oxazolone product from H⁺GGG-OH, although no atomistic details were provided. Other notable efforts examining water loss in peptides include pioneering work by Ballard and Gaskell with bigger peptides like bradykinin [69], leucine-enkephalin, and des-Arg¹-substance P(PKPQQFFGLM-NH₂) [70], H⁺AGG [49], dipeptides of glycine and cysteine [71, 72], and bigger peptides of glycine [15, 73, 74]. Here we have reexamined the mechanism in detail in SI and Supplementary Figure S9, at higher levels of theory than previously utilized. Briefly, loss of water occurs here by transfer of a proton to the C-terminal hydroxyl group, O⁴H, and subsequent ring formation. This occurs via the tight TS[O^1t-O⁴]-ct(cg)t{C~O⁴H}, which lies 107–136 kJ/mol above the GS and forms a complex of protonated 2-glycylaminomethyl-5-oxazolone, H⁺GAMOx[N³] and water. This complex can form the final products by losing H₂O via a loose TS, 107–116 kJ/mol above the GS and 4–22 kJ/mol below the TTS. Because this channel is limited by a TTS, it does not compete effectively with the pathways having loose TSs, explaining its small cross-section in Figure 1.

The TTS located here is similar to TS[O₁-O₃]-ctggt identified by Armentrout and Heaton for the formation of [b₂]⁺ by loss of water from H⁺GG [39] and to the TS found for loss of water from H⁺AGG [49]. The former study also located an alternative pathway involving TS[N₁-O₃]-ttgct, which can occur analogously for H⁺GGG by transfer of a proton from the N² nitrogen to the terminal hydroxyl group via TS[N²-O⁴]-(tg)tg(tg){C~O⁴H}; however, this pathway exceeds TS[O¹-O⁴]-ct(cg)t{C~O⁴H} by 78–97 kJ/mol (194–232 kJ/mol above the GS), Supplementary Table S5. The constrained head-to-tail cyclic geometry of this TS raises its energy and makes it entropically less favored as well. Thus, details of this route were not investigated further here. We also investigated the loss of water from [N¹]-ttggtgtt. This reaction pathway is limited by TS[N¹-O⁴]-(tg)tgg{C~O⁴H} that lies 16–26 kJ/mol higher than TS[O^1t-O⁴]-ct(cg)t{C~O⁴H}, Supplementary Table S5 and, therefore, was not explored further.

Bythell et al. [73] used tandem mass spectrometry, CID, and IRMPD to study dehydration from protonated tetraglycine, H⁺GGGG, and characterized the resultant product ion structure. They concluded that dehydration of H⁺GGGG occurs by elimination of a non-C-terminal oxygen atom resulting in an oxazole ring near the N-terminus and thus does not correspond to the [b₄]⁺ ion, which would otherwise require elimination from the C-terminal free acid end. Later, Verkerk et al. [75] re-examined the dehydration product of H⁺GGGG and reported a lower-energy protonated imidazolone product formed by the proton transfer from N-terminal amide oxygen. A similar reaction mechanism was also suggested by Spezia et al. for loss of water from H⁺GGGNH₂ [24], which has no hydroxyl group. Comparison of the experimental IRMPD spectrum with that calculated for the lowest energy water loss product led the authors to conclude that water loss occurs from the N-terminal residue. The possibility of such mechanisms was explored here but we were unable to find pathways lower in energy than the one in which water loss occurs from the C-terminus. Details of these alternative pathways can be found in SI. Notably, Spezia et al. [24] reported the formation of a [b₃]⁺ ion with an oxazolone structure similar to the present study, but this product is formed by the loss of ammonia from H⁺GGGNH₂.

In related experiments and computations on the [b₃]⁺ ion generated from a protonated pentapeptide, H⁺AAAAR, Allen et al. also found the oxazolone structure to be the lowest energy structure [57], which agrees well with the present results. These authors also located a nine-membered ring structure for their [b₃]⁺ ion, which lies 90 kJ/mol higher than the oxazolone structure. Similarly, we located a nine-membered ring structure, 2-hydroxy-5,8-dioxo-1,4,7-triazonane⁺[O] for our [b₃]⁺ ion, which is 69–85 kJ/mol higher in energy than H⁺GAMOx[N³], Supplementary Figure S9 and Supplementary Table S4. Because a lower energy pathway to form H⁺GAMOx[N³] was already found, we did not explore the pathway for the much higher energy cyclic [b₃]⁺ product ion.

Further Dissociation of [b₃]⁺ to [a₃]⁺

Decarbonylation of [b₃]⁺ to [a₃]⁺ is rarely observed [57, 58, 76], but is found here and for larger peptides [48, 51]. The lowest energy pathways for this process in the presence and absence of the water product are shown in Supplementary Figure S10. Although the former is lower in energy, the rate-limiting tight TS(H⁺GAMOx[N³]-ctgg){C~CO³}(H₂O_HN3,CO1•HO) along the pathway that includes water lies well above the loose TS associated with the [b₃]⁺ + H₂O products. Thus, the H⁺GAMOx(H₂O) intermediate should lose water rapidly, as demonstrated by calculations of the rate coefficients for this competition where the probability of reaching the TTS is four orders of magnitude less probable than water loss. Thus, decomposition of [b₃]⁺ to [a₃]⁺ probably occurs after water loss. Overall the formation of the [a₃]⁺ (GGNHCH₂ ⁺[N³]-ctggt) + H₂O + CO products is limited by the TTS, TS(H⁺GAMOx[N³]-ctg(cg)){C~CO³}, which is 223–256 kJ/mol above the GS. Here, the small magnitude of the [a₃]⁺ cross-section in Figure 1 is determined primarily by the cross-section magnitude of its [b₃]⁺ precursor.

In previous work, Allen et al. studied decarbonylation of the [b₃]⁺ ion from H⁺AAAAR [57] and explored the mechanism for this process in the absence of water. They found that the most stable [a₃]⁺ structure is a protonated linear imine structure formed by ring cleavage of [b₃]⁺ and is limited by a TTS. Both of these findings are similar to the results of the present study.

In an IRMPD study, Bythell, Maître, and Paizs (BMP) [51] compared the calculated IR spectra of the [a₃]⁺ structures with their experimental spectrum for [a₃]⁺ (from H⁺GGGG) and found that neither of the acyclic [a₃]⁺ structures gave a good match. Rather, a seven-membered ring structure (L by BMP), calculated to be ~23 kJ/mol below GGNHCH₂ ⁺[N³]-ctggt (A), agreed well with the IRMPD spectrum. Consequently BMP concluded that the majority of the [a₃]⁺ population is composed of the cyclic species (L) under the experimental conditions, which is kinetically the “most favored product” starting from GGNHCH₂ ⁺[N³]-ctggt (A) and formed by passing over a TTS 44 kJ/mol higher than A. This result motivated us to investigate cyclization of the [a₃]⁺ ion formed from H⁺GGG, which potentially can occur before or after losing water, although, as noted above, the water is probably lost upon formation of the [b₃]⁺ precursor (Supplementary Figure S10). Details of these pathways and the different [a₃]⁺ structures can be found in Supplementary Figures S11 and S12 of the SI. Overall, the rate-limiting TS for cyclization of [a₃]⁺ in the absence of water, TS(GGNHCH₂ ⁺[N³]-ctgg(tg)), lies 3–13 kJ/mol above the rate-limiting TS(H⁺GAMOx[N³]-ctg(cg)){C~CO³} for decarbonylation of the [b₃]⁺ ion, Supplementary Table S5. Thus, the acyclic [a₃]⁺ species GGNHCH₂ ⁺[N³]-ctggt should be formed at the experimental threshold, but cyclization can occur with little additional energy needed (although probably entropically disfavored). These theoretical results are not inconsistent with the observation of BMP that their [a₃]⁺ ion was dominated by the cyclic structure for two possible reasons: (1) this [a₃]⁺ ion was formed by decomposition of H⁺GGGG (rather than H⁺GGG), and (2), the source conditions needed to yield adequate amounts of [a₃]⁺ for spectroscopic study could provide additional energy needed for the cyclization.

Loss of CO and NH₃

The lowest energy pathway for the loss of CO and NH₃ from H⁺GGG begins after the loss of CO shown in Supplementary Figure S8 and parallels the mechanism elucidated previously for H⁺GG [39]. The path in Supplementary Figure S13 starts at the (CH₂NH₂ ⁺)(GG_{NH•OC,NH•N}) complex, but any low-energy variant of the (CH₂NH)H⁺(GG) complex can be used to initiate the loss of ammonia. A key finding of this pathway is covalent bond formation between the carbon of the immonium ion and the terminal nitrogen of GG. Depending on the level of theory, the products formed, CH₂GG⁺[N²]-tttttt + NH₃ + CO, lie above the rate-limiting TS for the initial CO loss (by ~10 kJ/mol at B3LYP-D3, Supplementary Figure S13, and 8 kJ/mol at M06-2X), and below this rate-limiting step by ~17 kJ/mol at the B3LYP and MP2 levels of theory, Supplementary Tables S4 and S5. Importantly, the products of this pathway lie 24–28 kJ/mol below the [y₂ + 2H]⁺ + CH₂NH + CO products, and thus are energetically favored although entropically disfavored because the latter products require no rearrangement from the starting complex, Supplementary Figure S8. As will be shown in the analysis of the data below, results from B3LYP and MP2 levels of theory appear to more reliably reproduce the experimental results.

We also examined another pathway involving the direct transfer of a proton from N² to N¹ but found its rate-limiting TS, TS(H⁺AMGG[N²-N¹]-(tg)gttttt) (Supplementary Figure S13), to be higher in energy, Supplementary Table S5. These two pathways are analogous to the low-energy mechanisms found by Armentrout and Heaton for loss of CO and NH₃ from H⁺GG, although the former pathway is the rate-limiting TS for the loss of CO + NH₃ from H⁺GG [39]. Bythell et al. [49] discovered a similar low-energy pathway for CO + NH₃ loss from H⁺AGG involving proton transfer from O² to N¹ and limited by the loss of CO (161 kJ/mol above GS H⁺AGG) at the B3LYP/6-31+G(d,p)//B3LYP/6-31G(d) level of theory.

An alternative pathway for the loss of CO + NH₃ from H⁺GGG involves nucleophilic displacement (S_N2 mechanism) of ammonia by the CH₂NH moiety in the CH₂NH(H⁺GG) complex formed after expulsion of CO. This mechanism results in rate-limiting TS[N²]-ttttt{CC~N²H}, which is 385–433 kJ/mol above the ground reactants, Supplementary Table S5. Further details of this pathway were not explored because Supplementary Figure S13 provides much lower energy pathways for deamidation following the initial decarbonylation. Similar results were also obtained by Bythell et al. for loss of CO + NH₃ from H⁺AGG [49] and by Armentrout and Heaton for the H⁺GG [39].

Analysis of Primary Dissociation Channels

Scheme 1 outlines the relationships between reactions 1–10 on the basis of the reaction mechanisms calculated above and previous work [39, 40]. The primary dissociations from H⁺GGG are the formation of [b₂]⁺ in reaction 1a, [y₁ + 2H]⁺ in reaction 2a, loss of water to form [b₃]⁺ in reaction 3, and loss of CO, which rapidly leads to formation of [y₂ + 2H]⁺ in reaction 5, [a₁]⁺ in reaction 7a, and loss of NH₃ in reaction 4. The rate-limiting TSs for [b₂]⁺, [y₁ + 2H]⁺, [y₂ + 2H]⁺, and [a₁]⁺ correspond to the asymptotic energies of their respective products (loose TSs), whereas TTSs limit the loss of water forming [b₃]⁺, TS[O^1t-O⁴]-ct(cg)t{C~O⁴H}, and loss of (CO + NH₃), TS[N²]-t_ttgttttt{N¹C~CO¹~N²C}, as detailed above. As noted, these TS characterizations are consistent with the relative magnitudes observed in Figure 1, namely, TTSs generally lead to small cross-sections and loose TSs lead to larger ones. Direct competition between [b₂]⁺ and [y₁ + 2H]⁺, where the former is clearly energetically favored, explains why the cross-section of the latter product is inhibited. Note that the primary product for CO loss (m/z 162) was not observed, which, given the mechanisms elucidated above, implies that this product decomposes rapidly when the thresholds for its subsequent decompositions are reached, primarily formation of [y₂ + 2H]⁺ and ammonia loss, and [a₁]⁺ at somewhat higher energies (all formed via loose PSL TSs according to theory). Because loss of CO over a TTS competes with the loose TS for the dominant [b₂]⁺ production at a similar energy, its cross-section apparently never reaches an appreciable level until after it can begin to dissociate further.

Scheme 1

Schematic reaction mechanism for H⁺GGG decomposition

These complex inter-related processes are analyzed by first summing the cross-sections of the major sequential channels with their precursor channels to form composite channels: m/z 115 + m/z 87 ([b₂]⁺ + [a₂]⁺ = [b₂]⁺ _tot), and m/z 133 + m/z 105 + high-energy (HE) portion (beyond 4 eV) of m/z 76 ([y₂ + 2H]⁺ + ([y₂ + 2H – CO]⁺) + [y₁ + 2H]⁺ _HE = [y₂ + 2H]⁺ _tot). The cross-section for [y₁ + 2H]⁺ _HE is isolated by subtracting the model for the low-energy (LE) portion from the [y₁ + 2H]⁺ _tot product cross-section. Channels [b₃]⁺ and [a₃]⁺ should also be summed, but the latter product is sufficiently small that it was not observed at lower pressures (as discussed further below). The cross-sections of the composite channels change smoothly with increasing energy, which is consistent with the assigned sequential dissociations, Figure 3. The cross-sections of the six primary channels, [b₂]⁺ _tot, [y₁ + 2H]⁺ _LE, [b₃]⁺, loss of CO + NH₃, [y₂ + 2H]⁺ _tot, and [a₁]⁺ are modeled competitively using Equation S1, as shown in Figure 3 with the optimized parameters listed in Table 1. This model provides the threshold energies for reactions 1a ([b₂]⁺), 2a ([y₁ + 2H]⁺ _LE), 3 ([b₃]⁺), 4 (loss of CO + NH₃), 5 ([y₂ + 2H]⁺), and 7a ([a₁]⁺). Cross-sections for [b₂]⁺ _tot, [y₁ + 2H]⁺ _LE and [y₂ + 2H]⁺ _tot can be modeled without scaling their cross-sections (i.e., using common σ _0,j values) or molecular parameters, suggesting that the statistical factors associated with these channels are sufficient to accurately describe their relative cross-section magnitudes over an extended energy range.

Table 1 Fitting Parameters of Equations S1, S3a, and S3b, Threshold Energies at 0 K, and Entropies of Activation at 1000 K for the Decomposition of H⁺GGG

It is important to point out that the modeling of the ammonia loss, [y₂ + 2H]⁺, and [a₁]⁺ cross-sections is not straightforward because theory shows that all three channels result from sequential decompositions from a product ion formed by CO loss. The challenge in modeling these three cross-sections as sequential decompositions is that the cross-section for the primary product ion (CO loss) was not observed. Our search for the best model for reproducing these three cross-sections led us to analyze these product cross-sections in three ways. These models are named after the TSs for NH₃ loss, [y₂ + 2H]⁺ formation, and [a₁]⁺ formation with subscripts designating their treatment as primary (P) or secondary (S) dissociations, namely T_PL_PL_P (tight-loose-loose), T_PL_SL_S (tight-loose-loose), and L_SL_SL_S (loose-loose-loose). In the latter model, the TS for initial CO loss is assumed to lie below the NH₃ loss products enough that its molecular parameters are inconsequential. Details of the analysis of the T_PL_SL_S (which requires extensive frequency scaling) and L_SL_SL_S (which does not reproduce the data) models can be found in the SI, because that discussion indicates that the best analysis of these three products is obtained by the T_PL_PL_P approach.

In the T_PL_PL_P model, shown in Figure 3, all three product channels are modeled as primary decompositions from H⁺GGG. Here, ammonia loss is analyzed as a primary product limited by the TTS for CO loss, which explains why the CO loss product is not observed. This is consistent with theory at the B3LYP and MP2 levels. Alternative TSs for CO loss are energetically similar to TS[N²]-t_ttgttttt{N¹C~CO¹~N²C} that was used to model reaction 4. Using different TSs in the analysis does not change the thresholds for the primary channels significantly; thus it is possible that the experimental threshold is a weighted average of the various TSs having similar energies leading to the same CO loss products.

The loose TSs for [y₂ + 2H]⁺ and [a₁]⁺ products involve dissociation to three molecular species (for which there are no appropriate statistical approaches yet developed). Therefore, when treated as “primary” dissociation channels, we use complexes of (CO + GG) and (CO + CH₂NH), respectively, as the “neutral” that is formed along with the primary ion to approximate the molecular parameters of the neutral products, CO + GG and CO + CH₂NH. Geometry optimizations were performed on different conformers of the putative (CO + GG) and (CO + CH₂NH) complexes to locate the lowest energy conformer, which was used in the data analysis. (GG-ctttt)(_OHOC), where the CO oxygen is H-bonded to the hydroxyl hydrogen of GG, was used to approximate the molecular parameters of CO + GG. Similarly, (CH₂NH)(_NCO), where the CO carbon is loosely coordinated to the CH₂NH nitrogen, was used to approximate the molecular parameters of CO + CH₂NH. The T_PL_PL_P model fits the [a₁]⁺ cross-section well only up to ~4.5 eV without the use of any cross-section scaling factor. The [a₁]⁺ cross-section can be accurately reproduced over the entire energy range shown if the PSL TS frequencies below 900 cm^–1 are loosened (multiplying by 0.813 ± 0.004) and the threshold is shifted up by 0.19 ± 0.09 eV, Table 1. The latter shift results because the kinetic shift is larger for the loose TS frequencies (compare ΔS₁₀₀₀ ^ǂ value of 243 with 207 J/mol K when TS frequencies were not scaled). The need for a scaling factor to reproduce the [a₁]⁺ cross-section over an extended range of energy indicates that [a₁]⁺ is formed via the PSL TS at threshold energies and by different pathways at higher energies. We believe that the [a₁]⁺ threshold energy obtained without the use of a scaling factor is our best threshold energy value for this product because it is not biased by the contribution of additional channels.

In order to accurately reproduce reaction 3 ([b₃]⁺) in the competitive modeling as shown in Figure 3, the TTS frequencies below 900 cm^–1 needed to be scaled by 0.786 ± 0.003. The need for this modest scaling of the vibrational frequencies indicates that the TTS is looser than suggested by theory. We also modeled the [b₃]⁺ cross-section using a switching TS in which the rate is determined by a low-energy TTS for H₂O loss coupled with a higher energy PSL TS. This model and its fitting parameters can be found in the SI. Here the PSL TS energy could be as high as 1.64 eV without affecting the reproduction of the [b₃]⁺ and other primary product cross-sections. At higher PSL TS energies, the model misses the threshold region of the [b₃]⁺ cross-section, Supplementary Figure S16. In comparison to the TTS model, the switching TS model does not require scaling of the cross-section or TS frequencies, such that the kinetic shift is larger, thereby reducing the [b₃]⁺ threshold energy by 0.20 ± 0.08 eV, Table 1 and Supplementary Table S6, which now agrees better with theory (as discussed below). Nevertheless, the model obtained using the TTS model reproduces the [b₃]⁺ cross-section better than the switching TS model, such that our best determination of the [b₃]⁺ threshold energy is an average value of the threshold energies obtained from these two approaches, 1.41 ± 0.09 eV, Table 1. This uncertainty includes a contribution from analyzing the [b₃]⁺ channel without the [a₃]⁺ product added.

We also analyzed the water loss [b₃]⁺ product using the high energy alternative TS, TS[N¹-O⁴]-(tg)tgg{C~O⁴H} (16–26 kJ/mol above TS[O^1t-O⁴]-ct(cg)t{C~O⁴H}), but this TS is entropically less favorable, such that the contribution from this TS should be minimal. Similarly, another high-energy TS, TS[N²-O⁴]-(tg)tg(tg){C~O⁴H}, is much higher in energy than TS[O^1t-O⁴]-ct(cg)t{C~O⁴H} and also more constrained (discussed above), such that it will not contribute significantly to the [b₃]⁺ channel.

All of these competitive products were also analyzed assuming that the reaction begins at the MP2 GS of H⁺GGG, [N¹]-ttggtgtt. The uncertainties in the threshold energies of all products examined here include deviations in the threshold energies associated with use of molecular parameters for either the [O¹] or [N¹] conformer in the data analysis.

Overall, Figure 3 shows that the competition between all six primary products can be modeled nicely over extended ranges of energy (>5 eV) and two and a half orders of magnitude. Note that in agreement with its large cross-section at high energies, [a₁]⁺ is entropically the most favored process among the six competitive channels as reflected in its large ΔS₁₀₀₀ ^ǂ value, Table 1.

Analysis of Secondary Dissociation Channels

Once the fitting parameters for the six primary channels are determined, sequential dissociation channels [a₃]⁺ (from [b₃]⁺), [a₂]⁺ (from [b₂]⁺), and [y₂ + 2H – CO]⁺ (from [y₂ + 2H]⁺) in reactions 6, 8a, and 9 are analyzed. In all of these analyses, threshold energies of the competing [b₂]⁺, [y₁ + 2H]⁺, [y₂ + 2H]⁺, and [a₁]⁺ channels are the same as those obtained when the sequential channels are not included. Other secondary dissociations include reactions 1b ([y₂ + 2H]⁺ – H₂O → [b₂]⁺) and 7b ([y₁ + 2H]⁺ – H₂O – CO → [a₁]⁺) that are not included in the current analysis because they are both inefficient processes that will contribute little to either product channel making it difficult to determine their energetics. In both cases, comprehensive studies have been done previously in our lab to yield threshold energies for these processes [37, 38].

The dissociation of [b₃]⁺ (m/z 172) to form [a₃]⁺ (m/z 144) in reaction 6 occurs by the loss of CO. Here the precursor [b₃]⁺ ion has low intensity such that the intensity of the [a₃]⁺ product ion is equally weak, and is also obscured by the nearby m/z 145 product ion, which is more intense. Because of these difficulties, zero pressure extrapolated cross-sections for the [a₃]⁺ product ion were of insufficient quality to model with any confidence. Therefore, we analyze the [a₃]⁺ product cross-section acquired at a high pressure (~0.2 mTorr) of xenon in order to obtain accurate relative threshold information. Calculations discussed above indicate there are two pathways leading to [a₃]⁺ + H₂O + CO, but the pathway associated with loss of water followed by decarbonylation of [b₃]⁺ is almost certainly operative, such that formation of [a₃]⁺ is limited by the tight TS(H⁺GAMOx[N³])-ctg(cg)){C~CO³}, Supplementary Figure S10. Thus, we analyzed the [a₃]⁺ product as a sequential loss of water followed by CO loss ([b₃]⁺ → [a₃]⁺) while still including the competition with the other five primary channels, Figure 4. Fitting parameters of the [a₃]⁺ product obtained from the analysis of high-pressure data are listed in Table 1. This analysis indicates that the threshold for reaction 6 is 0.81 ± 0.09 eV above that for reaction 3. When this difference is added to the threshold energy for formation of [b₃]⁺ determined using a zero-pressure extrapolated data set, we obtain a threshold for [a₃]⁺ production of 2.32 ± 0.12 eV.

The sequential dissociation of the primary [b₂]⁺ ion formed in reaction 1a to [a₂]⁺ in reaction 8a occurs via the tight TS(H⁺AMOx[N²]-c{OC~O}) as previously calculated by Armentrout and Clark [40]. The subsequent dissociation of [b₂]⁺ to [a₂]⁺ is modeled while still including competition from the other five primary product ions, Supplementary Figure S17. Here, the [a₂]⁺ ion required a slight scaling of its cross-section, which differs from Armentrout and Clark’s [40] analysis of [a₂]⁺ where no scaling was required. The sequential dissociation model reproduces the [a₂]⁺ cross-section up to ~4.5 eV. Analysis of the [a₂]⁺ cross-section beyond 4.5 eV does not reproduce the threshold region and requires extensive scaling of its cross-section to capture its magnitude. Above 4.5 eV, the [a₂]⁺ ion can also be made from a [b₂]⁺ product ion that is generated by dissociation of the primary [y₂ + 2H]⁺ product ion in reaction 8b, as shown directly in previous studies of H⁺GG decomposition [38]. These previous studies indicate that this pathway should start at ~4.5 eV (~2.5 eV above the apparent [y₂ + 2H]⁺ threshold), but is probably not a major contributor to the [a₂]⁺ cross-section above 4.5 eV, although the energy distributions involved in the sequential pathways from H⁺GGG might alter this conclusion. Nevertheless, analysis of the [a₂]⁺ data as a sequential dissociation from H⁺GGG via [b₂]⁺ formed in reaction 1a beyond 4.5 eV should not be accurate and explains the need for significant scaling of [a₂]⁺ cross-section at these higher energies. Supplementary Table S6 lists the parameters for this sequential fit. We find the threshold energy of the [a₂]⁺ product to be 3.39 ± 0.06 eV when formed by reaction 8a, which lies 1.62 ± 0.08 eV above the threshold for [b₂]⁺ (whose average threshold energy is 1.77 ± 0.06 eV, Table 1). The 1.62 ± 0.08 eV value can be favorably compared with a threshold energy of 1.57 ± 0.12 eV found for the same process in a previous study [40].

Armentrout and Heaton [38] also found that the [b₂]⁺ product ion can dissociate to [a₁]⁺ via [a₂]⁺, reaction 7c. Here, we explored this possibility by summing the [a₂]⁺ and [a₁]⁺ cross-sections and fitting this composite channel as a sequential dissociation from [b₂]⁺ where formation of [a₂]⁺ is limited by the tight TS(H⁺AMOx[N²]-c{OC~O}). We also analyzed the [a₁]⁺ cross-section as a sequential dissociation from [b₂]⁺, limited by a PSL TS. These analyses show that the threshold energy of [a₁]⁺ (from [b₂]⁺) exceeds that of [a₂]⁺ (from [b₂]⁺), thus indicating that [b₂]⁺ forms [a₂]⁺ first, which then dissociates to [a₁]⁺, consistent with previous results [40]. However, the threshold energies obtained for [a₁]⁺ and [a₂]⁺ differ by only 0.20 eV, which is much smaller than the difference of 1.36 eV [40] obtained previously for dissociation of [b₂]⁺. This comparison simply confirms that [b₂]⁺ contributes to the [a₁]⁺ product at higher energies and that other processes dominate the onset for production of [a₁]⁺. This result is consistent with a recent study conducted by Bythell and Harrison where the direct [b₂]⁺ → [a₁]⁺ pathway was found to be insignificant for a [b₂]⁺ ion having a glycylglycine sequence [59].

Lastly, we analyze the secondary dissociation of H⁺GGG in reaction 9, decarbonylation of the primary [y₂ + 2H]⁺ _tot product formed in reaction 5. As mentioned above, the direct study of H⁺GG ([y₂ + 2H]⁺) revealed that the ([y₂ + 2H – CO]⁺) product ion formed after CO loss can undergo further fragmentation to form the [y₁ + 2H]⁺ product ion. As in that study, the composite cross-section was modeled as a sequential loss of CO from [y₂ + 2H]⁺ limited by tight TS[N²]-ttgtt{C^α1~OC~N²} [39], while still including competition with the major primary channels: [b₂]⁺, [y₁ + 2H]⁺, and [a₁]⁺. In this data analysis, we used a complex of CO and CH₂NH to approximate the molecular parameters of the “neutral” formed after CO loss from the primary ion [y₂ + 2H]⁺ because this dissociation involves three molecular species. This assumption was not needed in the previous study because CO was the only neutral formed in that system. Our sequential model requires no scaling of the cross-section of reaction 9 similar to the previous analysis of this product [38], and reproduces the data well in the threshold region and up to ~5 eV, Supplementary Figure S18. The threshold energy of the [y₂ + 2H – CO]⁺ product from our analysis is 3.91 ± 0.13 eV, which lies 1.63 ± 0.14 eV above the [y₂ + 2H]⁺ (H⁺GG) threshold and agrees well with the energy obtained previously for the dissociation of H⁺GG, 1.62 ± 0.05 eV [38]. The result of this sequential model, along with its optimized parameters, is listed in Supplementary Table S6. Analysis of the composite cross-section of reaction 9 beyond 5 eV (1.4 eV above the apparent threshold for [y₂ + 2H]⁺) cannot be performed accurately because the [y₂ + 2H – CO]⁺ product decomposes to [y₁ + 2H]⁺ _HE starting ~1.5 eV above the onset for [y₂ + 2H]⁺, as shown by previous studies of H⁺GG.

Analysis of Tertiary Dissociation Channels

Decomposition of H⁺GGG also produces third-order dissociation products: [y₁ + 2H]⁺ _HE in reaction 2b, [a₁]⁺ in reaction 7c, [a₂]⁺ in reaction 8b, and H⁺(CH₂NH)₂ in reaction 10. None of these reactions can be modeled directly in the present system because our data analysis program CRUNCH cannot handle such high order reactions for reasons noted above. However, formation of [a₁]⁺ from H⁺GG ([y₂ + 2H]⁺ → [y₂ + 2H – CO]⁺ → [a₁]⁺) and [a₂]⁺ from H⁺GG ([y₂ + 2H]⁺ → [b₂]⁺ → [a₂]⁺) have been analyzed previously in our lab yielding their threshold energies [38]. These previous studies on H⁺GG decomposition also indicate that [y₁ + 2H]⁺ _HE formed in reaction 2b follows the loss of CO from [y₂ + 2H]⁺ _tot [38, 39]. Beyond 5 eV, [y₁ + 2H]⁺ _HE is the only contributor to the composite cross-section for reaction 9 ([y₂ + 2H – CO]⁺ + [y₁ + 2H]⁺ _HE) such that the threshold energy of reaction 9 beyond 5 eV is the threshold energy of the [y₁ + 2H]⁺ _HE product. Analysis of the composite cross-section for reaction 9 as a sequential dissociation from [y₂ + 2H]⁺ _tot requires slight scaling of the cross-section and yields a threshold energy of 4.28 ± 0.11 eV, Supplementary Figure S19. This is 2.00 ± 0.13 eV above the threshold energy of [y₂ + 2H]⁺ (H⁺GG), which agrees with the previously measured threshold energy of 1.98 ± 0.07 eV [38] for the same process. A detailed description of this analysis that accounts for the differences in this process when formed from H⁺GGG versus from H⁺GG can be found in the SI. Optimized parameters of this model are listed in Supplementary Table S6.

Decomposition of the [a₂]⁺ product to form H⁺(CH₂NH)₂ in reaction 10 was observed in a previous study of the decomposition of the [b₂]⁺ ion [40] with a threshold energy of <2.50 ± 0.31 eV [40]. This work showed that reaction 10 is limited by tight TS(C₃H₇N₂O⁺[N²]-ct{C~OC~N}). Here, we find the threshold energy for formation of [b₂]⁺ is 1.77 ± 0.06 eV, such that a fair estimate of the threshold energy for H⁺(CH₂NH)₂ formation is the sum of these two energies, <4.27 ± 0.32 eV. This value is somewhat lower than the apparent threshold of ~4.9 eV for the H⁺(CH₂NH)₂ product, Figure 1, but this would be expected because of the competition inherent in this more complicated system.

Comparison with Previous Experiments and Theory

In their study, KK [14] obtained the threshold energies for dissociation of H⁺GGG into the two primary channels, [b₂]⁺ and [y₂ + 2H]⁺, using an early version of CRUNCH. They obtained threshold energies of 2.36 and 3.17 eV, respectively, although neither value includes competitive or kinetic shifts. An estimate for kinetic shifts on the basis of their results for the H⁺GG system yielded a more reasonable threshold energy value of <1.65 eV for [y₂ + 2H]⁺. If we independently analyze the present data for [b₂]⁺ and [y₂ + 2H]⁺ without considering competitive or kinetic shifts, we obtain threshold energies of 2.04 ± 0.09 and 3.05 ± 0.08 eV, respectively, which are similar to the values of KK. When competitive and kinetic shifts are included, our threshold for the [y₂ + 2H]⁺ channel is 2.28 ± 0.06 eV, well above the threshold estimated by KK, which simply points out the limitation of their estimate.

Aribi et al. [16] obtained a threshold energy of 1.37 (+0.10/–0.12) eV for the [b₂]⁺ ion including kinetic shifts and 2.81 eV without including kinetic shifts. These values differ wildly from our average values of 1.77 ± 0.06 and 2.04 ± 0.09 eV, respectively. As discussed in detail by Armentrout and Clark in their study of the [b₂]⁺ ion formed from H⁺GGG [40], the [b₂]⁺ cross-section reported in the earlier study is shifted to higher energies and has an inflated cross-section, explaining why the thresholds without kinetic shifts differ. Once kinetic shifts are included, the difference between these threshold energies can be attributed to the choice of the rate-limiting TS used for data analysis. Aribi et al. used a tight TS [16], which should lead to a larger kinetic shift (1.44 eV) and lower threshold energy. In contrast, we find the [b₂]⁺ product to be limited by a loose PSL TS, Supplementary Figure S6, such that the kinetic shift is modest (0.27 eV).

Comparison with Theoretical Results

Figures 3, 4, and Supplementary Figures S14–S19 show that the experimental cross-sections for reactions 1a, 2a, 2b, 3–7a, 8a, and 9 are reproduced well by Equations S1, S3a, and S3b, over a wide range of energies (up to 4–6 eV) and over two orders of magnitude in cross-section. One additional means of evaluating the success of this analysis is to compare the experimental threshold energies obtained from the modeling with those obtained from calculations. Comparison of the experimental threshold energies of reactions 1a, 2a, 2b, 3–7a, 8a, 9, and 10 with 0 K values for the rate-limiting TSs for each channel calculated at the B3LYP, B3LYP-D3, MP2, and M06-2X levels of theory is shown in Table 2 and Figure 5.

Table 2 Comparison of Experimental and Theoretical Reaction Energies at 0 K for Decomposition of H⁺GGG in kJ/mol

In general, agreement between theory and experiment is reasonable with bigger differences between theory and experiment for the higher energy sequential dissociations. Thus, we first compare the mean absolute deviations (MADs) from experimental threshold values excluding these products. All four levels of theory yield between two and four threshold values that agree with experiment within the uncertainties. The MADs for the six primary products are similar for all four levels of theory, 6–14 kJ/mol. These MADs compare well with those of ~10 kJ/mol found previously in our laboratory for the decompositions of H⁺GG, H⁺G, and H⁺Asn systems [37, 38, 77]. At least two theoretical values fall within our range of experimental uncertainty for all primary products except reaction 5. For reaction 5 ([y₂ + 2H]⁺), theory underestimates the threshold energy by 13–46 ± 6 kJ/mol. As noted above, our modeling is speculative for this product channel because theory indicates its formation involves dissociation to three molecular species (one ion and two neutrals), whereas our best modeling (T_PL_PL_P) assumes [y₂ + 2H]⁺ is formed as a primary product, i.e., dissociation occurs to one ion and one neutral (a loose complex of the two neutral species). This approach may over-estimate the true threshold energy because competition between the other primary products and the TTS for CO loss is not adequately represented.

For the secondary products, [a₃]⁺, [a₂]⁺, and [y₂ + 2H - CO]⁺, and tertiary products, [a₂ – CO]⁺ and [y₁ + 2H]⁺ _HE, at least one theoretical value is within experimental uncertainty. If all 11 fragmentations from H⁺GGG are considered, the MADs increase to 13–29 kJ/mol, Table 2. Clearly, M06-2X level of theory gives the best agreement with experiment when the primary and when all products are considered, although the deviations are reasonable for all levels of theory. Overall, the good agreement between experiment and theory, especially for the primary products, validates the reaction mechanisms described above.

We can also compare the energy difference between the TS energy for CO loss and the sequential products [y₂ + 2H]⁺ and [a₁]⁺ that follow this putative primary product. Calculations suggest that the TS energy for CO loss is 6–36 kJ/mol below the [y₂ + 2H]⁺ PSL TS and 63–94 kJ/mol below the [a₁]⁺ PSL TS. Modeling the experimental data suggests that these differences are <57 kJ/mol for [y₂ + 2H]⁺ and <102 kJ/mol for the [a₁]⁺ product, consistent with theory.

We can also favorably compare the energy measured here for the subsequent decomposition of the [b₂]⁺ ion in reaction 8a, 156 ± 8 kJ/mol, with that measured previously for the direct dissociation of [b₂]⁺: 151 ± 12 kJ/mol [40]. Similarly, the subsequent dissociation of the [y₂]⁺ ion to lose CO in reaction 9 is measured here to cost 157 ± 14 kJ/mol, which can be compared with the CO loss threshold energy of 157 ± 7 kJ/mol for the same fragmentation of H⁺GG measured previously in our laboratory. Further, the threshold energy of reaction 2b involving the sequential dissociation of [y₂ + 2H]⁺ to [y₁ + 2H]⁺ _HE is found to be 193 ± 11 kJ/mol above that of [y₂ + 2H]⁺, which is consistent with 191 ± 7 kJ/mol measured previously [38].

Conclusion

In the present study, we have examined the conformers of H⁺GGG using B3LYP, B3LYP-D3, MP2, and M06-2X levels of theory. The lowest energy [O^1t]-ctgttttt structure predicted by B3LYP and B3LYP-D3 agrees with the ground structure (GS) obtained previously by PS [18] and WM [60]. MP2 and M06-2X suggest that [N¹]-gcgttgtt is the lowest energy structure and is lower than the [N¹]-ttggtgtt GS previously suggested by the MP2 calculations of WM. Comparison of the calculated spectra for [O^1t]-ctgttttt, [N¹]-gcgttgtt, and the low-lying [N¹]-ttggtgtt and [N¹]-tcgctgtt conformers with the IRMPD spectrum obtained by WM indicate that [O^1t]-ctgttttt and [N¹]-ttggtgtt are the dominant species formed under experimental conditions, in agreement with the previous conclusions of WM (who did not consider the other two [N¹] conformers). Examination of the neutral GGG and pathways for cis-trans isomerization of H⁺GGG indicate that the [N¹]-gcgttgtt and [N¹]-tcgctgtt conformers, both of which have a cis peptide bond between the first and second residues, are unlikely to be formed in solution or in the electrospray ionization process, explaining why they are not obvious species in the IRMPD spectrum. The presence of both [O^1t]-ctgttttt and [N¹]-ttggtgtt is consistent with MP2 populations calculated at 298 K, whereas B3LYP, B3LYP-D3, and M06-2X energies would suggest that only the [O^1t] species should be present. We also find that interconversion of [N¹]-ttggtgtt and [O^1t]-ctgttttt requires surmounting an appreciable barrier, indicating that both species are probably formed directly in solution or the electrospray ionization process. Interconversion can occur after collisional activation, however, such that both isomers share common rate-limiting TSs for decomposition.

The [b₂]⁺ (H⁺AMOx) and [y₁ + 2H]⁺ (H⁺G) product ions are formed competitively via the “oxazolone” pathway, comparable to the results of PS, and are limited by the separated product energies and, thus, their transition states are loose, Supplementary Figure S6. CO loss from H⁺GGG has a tight TS and can occur through three similar pathways, with the lowest energy pathway lying 164–175 kJ/mol above the GS (slightly lower in energy than the pathway found by PS). Loss of CO from H⁺GGG forms a (CH₂NH₂ ⁺)(GG) complex, which dissociates competitively to form ionic products [y₂ + 2H]⁺ (H⁺GG) and [a₁]⁺ (CH₂NH₂ ⁺) via loose rate-limiting TSs, Supplementary Figure S8. At somewhat lower energies, the (CH₂NH₂ ⁺)(GG) complex can also rearrange and lose a molecule of ammonia, Supplementary Figure S13, which is limited by the initial loss of CO at 164–175 kJ/mol at the B3LYP and MP2 levels, a result that is largely confirmed by the analysis of the present data. The loss of water from H⁺GGG has a tight TS, Supplementary Figure S9, and results in the formation of the [b₃]⁺ product, H⁺GAMOx, which has an oxazolone structure similar to [b₂]⁺ with an additional glycyl group. Further cleavage of the oxazolone ring of the [b₃]⁺ product can release CO and form [a₃]⁺, Supplementary Figure S10. Because loss of water from H⁺GAMOx(H₂O) is both energetically and entropically more favorable than the decarbonylation, Supplementary Figure S10, these processes are likely to occur sequentially in the experiment. Loss of CO from [b₃]⁺ is limited by a tight TS that forms an acyclic ion, [a₃]⁺ (GGNHCH₂ ⁺); however, cyclization of GGNHCH₂ ⁺ can take place to form a seven-membered ring conformer with little additional energy (although the extra step makes it entropically less likely to occur).

The kinetic energy dependence of the collision-induced dissociation of H⁺GGG with Xe is examined in a guided ion beam tandem mass spectrometer. Kinetic energy-dependent cross-sections for six primary products: [b₂]⁺, [y₁ + 2H]⁺ _LE, [b₃]⁺, CO loss, [y₂ + 2H]⁺, and [a₁]⁺; three secondary products: [a₂]⁺, [a₃]⁺, and [y₂ + 2H – CO]⁺; and two tertiary products: [y₁ + 2H]⁺ _HE and [a₂ – CO]⁺ are observed and analyzed. Threshold energies at 0 K for all of these processes are determined after consideration of the effects of multiple collisions with Xe, internal energy, lifetime effects, and competition [78–80]. Notably, this work entails the first simultaneous analysis of six product channels, with reasonable results obtained for their threshold energies. Experimental results are compared with detailed quantum chemical calculations discussed above. Thresholds for reactions 2a ([y₁ + 2H]⁺ _LE), 3 ([b₃]⁺), 4 (CO loss), 6 ([a₃]⁺), and 7a ([a₁]⁺) constitute the first experimental measurements, and those for reactions 1a ([b₂]⁺) and 5 ([y₂ + 2H]⁺) have been refined to provide more accurate thermodynamics for these two products. We find that the threshold energy values of all reactions (except reaction 5) lie within experimental uncertainty of at least one of the four theoretical values. This good agreement validates the reactions mechanisms explored theoretically and also allows identification of the structures of the products formed at threshold. The discrepancy between the experimental and theoretical threshold energies of the [y₂ + 2H]⁺ primary product in reaction 5 is attributed to its more speculative data analysis. Comparison of the threshold energies of primary products with theory indicates that the four levels of theory give MADs of 6–14 kJ/mol, with M06-2X giving the best agreement. Threshold energies of reactions 2b ([y₁ + 2H]⁺ _HE), 8a ([a₂]⁺), 9 ([y₂ + 2H – CO]⁺), and 10 ([a₂ – CO]⁺) are consistent with those measured previously in our laboratory for the same products [38, 40].

Good agreement between experimental and theoretical energies also indicates that the reactions begin at the ground conformation (or those conformations populated within a thermal equilibrium). Formation of the products observed in the decomposition of H⁺GGG requires that the extra proton is able to move. Reaction mechanisms in the present study clearly show that the extra proton is mobile once the ground state reactant is collisionally activated. Thus, these results provide a detailed exposition of the utility and scope of the mobile proton model [6, 27] in understanding fragmentations of the simplest tripeptide. Overall, these results hopefully can be used to better predict mass spectra and, thus, improve our understanding of the fragmentations of larger peptides and also improve the algorithms used to predict sequences [81].

As noted above, the ability to obtain accurate thermodynamic information allows a comparison with theoretical results, which permits the identification of the structures of products. Thus, TCID methods provide a similar component of structural identification as spectroscopic approaches, while additionally yielding valuable thermodynamic information. Notably, such structures need not always agree depending on whether the ion sources and conditions used to generate adequate product ion intensity for spectroscopic interrogation allow subsequent isomerization. In this regard, it is also interesting to contemplate how large a peptide can be studied by TCID. Clearly, larger peptides will exhibit increasing kinetic shifts resulting from increased degrees of freedom, which will limit the accuracy of the kinetic modeling needed to extract useful threshold information. Further, slower processes (those occurring via TTSs) may not be observed within the experimental time-frame available. Given the success of the present study in comprehensively examining a tripeptide, we conservatively speculate that accurate studies of hexapeptides should be feasible in the future.

Another important finding of this work is that the data analysis does not demand that we have exact knowledge of the rate-limiting TSs involved in these reactions. In fact, the magnitude of the experimental cross-section of a particular product generally indicates the nature of the rate-limiting TS involved in that reaction. For instance, the large cross-section of [b₂]⁺ indicates that it is dictated by a loose TS, whereas the small cross-section for the [b₃]⁺ product suggests that it is formed via a tight TS. Thus, the data determines whether a particular product is formed via a tight or loose TS, such that adjustment of the relative tightness or looseness of the TS (in the form of ΔS^†) should enable accurate analysis of the data. Consequently, for more complex systems, a generic set of vibrational frequencies and rotational constants (which can be modified to fine-tune ΔS^†) as input should suffice for data analysis.