FormalPara Key Summary Points

Why carry out this study?

Chronic kidney disease (CKD) in type 2 diabetes mellitus (T2DM) is associated with a substantial clinical and economic burden globally

Evaluating new treatment options, including renoprotective drugs, requires accurate computer simulation models of CKD in T2DM, which were reviewed systematically in this study to identify model structures and approaches and data sources used, to inform future model development

What was learned from the study?

Computer simulation models of CKD in T2DM focused on albuminuria and end-stage kidney disease, with relatively few models capturing CKD regression or remission, or employing glomerular filtration rate (GFR) for modeling

Central data sources informing models were predominantly from high-income countries and White populations, but several recent models were developed from country-specific data for Asian countries or from large outcomes trials

The models and data sources identified in this review can be used as a starting point to develop new or update existing CKD models for T2DM, especially when combined with recent clinical findings on albuminuria and GFR trajectories and new data sources on CKD treatments

Introduction

Chronic kidney disease (CKD) affects nearly one in ten people globally—approximately 700 million people—and was responsible for an estimated 1.2 million deaths in 2017 [1]. By 2040, CKD is projected to rank among the five leading causes of years of life lost [2]. Healthcare spending related to CKD is already substantial: US Medicare costs for CKD and end-stage kidney disease (ESKD) in 2017 exceeded US dollars (USD) 120 billion or one in every three fee-for-service dollars spent by Medicare [3]. Among commercially insured US patients with newly recognized CKD and type 2 diabetes mellitus (T2DM), total costs were USD 24,029 per person per year, while mean total healthcare-related CKD costs in Spain were euros (EUR) 14,533 in 2019 [4, 5].

More severe CKD increases the risk of adverse clinical outcomes, in particular cardiovascular disease (CVD) and mortality [6, 7], and necessitates more intensive and more expensive therapy, including renal replacement therapy (RRT) such as dialysis or kidney transplant [8]. For example, among commercially insured US patients with CKD, microalbuminuria, and T2DM, per-person per-year costs were USD 18,529 in patients with CKD stage 1, compared with USD 110,210 in patients with CKD stage 5 [4]. Similar findings were reported for Germany, where mean per-person annual costs for were EUR 8030 for patients in CKD stage 3 relative to EUR 44,374 for dialysis-treated patients [9], and for Italy, where mean direct healthcare costs per patient in the first year of treatment with erythropoiesis-stimulating agents were EUR 8917 for patients in CKD stages 1–3 compared with EUR 31,985 for dialysis-treated patients [10]. In China, the mean annual costs for hemodialysis and peritoneal dialysis were Chinese yuan (CNY) 94,761 and CNY 80,763 per patient, compared with CNY 132,253 and CNY 93,155 per patient with a kidney transplant in the first and second year, respectively [11].

Clinically, CKD is defined as kidney structure or kidney function abnormalities present for more than 3 months and classified using glomerular filtration rate (GFR) and albuminuria [12]. As part of this classification, GFR is conventionally grouped into five stages that, together with albuminuria, inform patient prognosis [12, 13]. The classical phenotype of CKD, both with and without T2DM, has been a linear decline in estimated GFR (eGFR) in the presence of persistent albuminuria [14]. Alternative disease trajectories have recently been described, including eGFR declines in diabetes in the absence of albuminuria [15] as well as non-linear, non-progressive, and variable eGFR trajectories [16, 17], with the latter being linked to outcomes such as ESKD, initiation of RRT, and mortality [18, 19]. While CKD remains a progressive disease in most patients, CKD is not irreversible and may regress, to the extent that CKD regression and death are more probable with advancing age than CKD progression and kidney failure [20, 21].

Metabolic conditions such as obesity and diabetes are among the main risk factors for CKD and increase the risk of non-CKD sequelae in patients with CKD [22,23,24]. Diabetes, in particular, is an independent risk factor for kidney damage, prevalent in almost two-thirds of patients with CKD, and will contribute substantially to the projected increase in worldwide CKD cases [23, 25, 26].

The treatment of CKD in T2DM has recently advanced, after a prolonged period with limited progress in therapeutic options, by the availability of novel drug classes including sodium-glucose cotransporter 2 (SGLT2) inhibitors, such as canagliflozin and dapagliflozin, and mineralocorticoid receptor agonists, such as finerenone [22, 27, 28].

SGLT2 inhibitors have been shown to have cardio- and renoprotective effects, as evaluated by improvements in eGFR and albuminuria and in clinically relevant endpoints, and they reduce mortality in patients with T2DM and at different stages of CKD [27, 29,30,31]. A systematic review and meta-analysis of trials for empagliflozin, canagliflozin, and dapagliflozin in patients with T2DM showed that the risk of dialysis, transplant, and death due to kidney disease was reduced by 33%, and risk of ESKD was reduced by 35% with SGLT2 inhibitors relative to placebo, with benefits observed across eGFR subgroups and albuminuria levels at baseline [32]. A similar analysis of cardiovascular outcomes trials in T2DM showed that use of SGLT2 inhibitors was associated with reductions in worsening eGFR, ESKD, or renal death risk of between 36% and 52% [33]. Similarly, an additional meta-analysis of six placebo-controlled trials of SGLT2 inhibitors, including five trials conducted in populations with T2DM, showed that SGLT2 inhibitors were associated with reduced risk of worsening kidney function, ESKD, or kidney death as well as reduced all-cause mortality, irrespective of metformin use [30].

Clinical trials and reviews building on them can establish the efficacy and safety of a novel therapy only over a limited time horizon. Long-term assessments of benefits and costs instead often rely on computer simulation models. Such modeling is challenging given the complexity of CKD and diabetes and the considerable number of risk factors and adverse clinical outcomes that could be considered in a model, subject to the availability of appropriate data.

Given the increasing need for modeling CKD in T2DM to inform clinical and economic decision-making around novel treatment options, the present study aimed to provide a comprehensive and current reference on modeling CKD in T2DM based on a systematic literature review of existing models. The work was motivated by a 2019 review [34] of CKD models in general, relative to which the present study provides an updated focus of CKD modeling specifically in T2DM and adds a review of modeling data sources, including their clinical and geographical representativeness.

Methods

A systematic literature review was conducted and reported in line with the Preferred Reporting Items for Systematic Reviews and Meta-Analyses 2020 (Table S1 in the Supplementary Material) [35]. The review protocol was not registered but is available from the corresponding author. This article is based on previously conducted studies and does not contain any new studies with human participants or animals performed by any of the authors.

Eligibility Criteria

The Population, Intervention, Comparator, Outcomes, Study Design approach was used to define study eligibility, albeit with no restrictions on interventions or comparators. Studies were eligible for inclusion if they were computer simulation models (study design) of kidney disease or kidney markers (outcomes) in patients with T2DM (population), regardless of the intervention and comparators used (Table S2 in the Supplementary Material).

In line with a 2008 definition by Stahl, a model was considered as a “simplified representation of reality that captures some of that reality’s essential properties and relationships” [36]. Specifically, computer simulation models of CKD were considered, including cohort state-transition models (cSTM)—or models that could be evaluated as such—and risk equation-based individual patient simulations (IPS), designed to project disease outcomes over time. Models were not required to report health economic outcomes, but studies that developed only risk predictions or nomograms were not eligible.

Studies were not eligible if they did not assess the progression of renal disease (but instead employed only a single renal-related state/event) or if they were cases using models already included in the review (published updates to existing models were considered to inform data extraction but were not counted as separate or new models). The latter criterion was used to avoid the inclusion of studies that used existing models such as the CORE Diabetes Model [37] to investigate a specific intervention in a particular setting, without making or reporting changes to the model.

Studies were also excluded if they provided no or insufficient detail on the renal model, e.g., if a model was only briefly described in a conference abstract (searches were conducted on the basis of model name, if any, as well as on first and last author names to identify if full publications were available and eligible for inclusion). As the focus of the review was on modeling CKD, not on the clinical efficacy of specific interventions, clinical studies were also not eligible.

Information Sources and Search Strategies

Searches were conducted in PubMed (including MEDLINE), Embase, and the Cochrane Library, using the respective search interfaces, on February 12, 2021, with incremental identical searches for newly added studies conducted on March 6 and October 8, 2021, as data extraction progressed on the models identified in the initial search.

Search strategies were adapted from those published by Sugrue et al. [34] by limiting the search to T2DM and by widening the focus from health economic models to modeling studies in general. Search strategies combined terms from the Medical Subject Heading and Emtree controlled vocabularies with free-text terms for renal complications, T2DM, and modeling studies. Initially developed for PubMed (Table S3 in the Supplementary Material), search strategies were subsequently mapped to Embase (Table S4 in the Supplementary Material) and the Cochrane Library (Table S5 in the Supplementary Material). Reference lists of eligible articles were also searched for relevant publications.

For searches in PubMed and the Cochrane Library, no limits were imposed on dates of coverage. For Embase, search results also available from MEDLINE were excluded to avoid duplicates, and abstracts identified in Embase were excluded if published before 2019 as it was assumed that a full peer-reviewed paper would have been published by the time of final search implementation in late 2021.

Study Selection and Data Collection

Results from literature searches were retrieved and stored using the literature review platform Sourcerer (Covalence Research Ltd, London, UK) [38]. After the removal of duplicate hits, the titles and abstracts of the remaining unique hits were screened against inclusion criteria by a single researcher. Subsequently, full texts of articles retained after title-abstract screening were screened, again by a single researcher, to determine final inclusion or exclusion. Ten percent of hits were screened by a second researcher, with any discrepancies resolved through consensus.

Data were extracted by a single researcher into a Google Sheets (Google LLC, Mountain View, CA, US) workbook. The extracted data included information on model design, structure, and setting, including, for example, year of publication, country setting, research goals, model type, and number of kidney disease-related states/events; risk equation parameters; data on possible transitions and transition probabilities in state-transition models; data sources used by models (where possible, by specific data point in the model); and baseline clinical and demographic characteristics of derivation cohorts in the primary clinical sources. A detailed list of variables is provided in Table S6 in the Supplementary Material. For models of both type 1 and 2 diabetes mellitus, data were extracted from the T2DM component of the model if sufficient detail was available.

The risk of bias within and across studies as well as the certainty and heterogeneity of results were not assessed as they were not considered relevant for the current review given the focus on model structures rather than outcomes. Similarly, specific model results, e.g., on the long-term benefits or economic characteristics of specific interventions, were not extracted.

Synthesis Methods

All statistical summaries were descriptive, including means, standard errors, and proportions to summarize model characteristics across the pool of models under consideration. All statistical analyses were based on complete cases, i.e., using all data available for a specific analysis. Data preparation and analyses [39,40,41,42,43] and plotting [44,45,46,47,48,49,50,51,52,53] were conducted using version 4.1.1 of the R statistical programming language [54, 55].

Models and primary sources were conceived of and plotted as a co-occurrence network [56,57,58]. Two simple measures of centrality were calculated to evaluate the importance of specific datasets to the CKD modeling in T2DM: degree centrality (the number of edges a node has) as a measure of “popularity”, and eigenvector centrality (accounting, for each node, for the centrality of the other nodes it is connected to) as a measure of “prestige” [59]. A core set of sources was identified by ranking sources on both measures of centrality; core sources were defined as any source ranked within the ten most central sources on at least one of the two centrality measures. For the analysis of model–data source relationships, only primary sources—sources that reported original data, such as clinical trials, observational studies, or CKD registers—were considered. If a source was a synthesis of previous sources, e.g., a meta-analysis, the underlying primary sources were identified and included.

For primary sources, the time “lag” between the source data cutoff and model publication was analyzed. The source data cutoff was established as follows: where reported, the end of the study or follow-up period was used. Otherwise, if the end of study or follow-up could be estimated from latest year of baseline enrolment and the reported follow-up time, this estimate was used. If the year so calculated was later than the year of publication or if no year could be calculated, the date of submission to the journal was used. If neither was reported, the year of publication was assigned.

For the analysis of baseline data from derivation cohorts, the publication with the largest sample size was chosen if more than one publication was available reporting on a single clinical data source; publications with smaller sample sizes were deemed more likely to be subgroup analyses. If a study reported baseline data separated across groups, e.g., by sex or by treatment arm, mean values weighted by the sample size in each group/arm were calculated. Biomarkers reported in different units, e.g., as mg/dL and mmol/L for lipids, were converted to a common unit for each biomarker (Table S7 in the Supplementary Material).

Baseline data were combined across studies using arithmetic means, weighted by the logarithm of sample sizes (except for ethnicity proportions, which were calculated from untransformed sample sizes). Values reported as medians were converted to arithmetic means using the Box–Cox method proposed by McGrath et al. [60], while values reported as geometric means were converted using the methods outlined by Higgins et al. [61].

Results

Study Selection and Characteristics

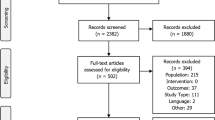
The literature and reference list searches identified 2995 records, of which 435 were duplicates (Fig. S1 in the Supplementary Material). Titles and abstracts of the remaining 2560 unique records were screened, leading to exclusion of 2478 records. Full texts of the remaining 82 studies were reviewed, leaving 49 computer simulation models of CKD in T2DM for inclusion in the review (Table 1 and Table S8 in the Supplementary Material).

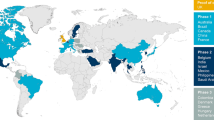
Table 1 Computer simulation models of T2DM included in the review
Full size table

Of the 49 models, most had been developed for the USA (n = 14) or the UK (n = 6), nine had been developed for Asian countries (Japan, n = 3; Thailand, n = 3; China, n = 2; Taiwan, n = 1), and one for a Latin American country, Columbia (Fig. S2 in the Supplementary Material). Two models were developed explicitly for a multinational setting while six were not reported as being specific to any geographical setting. Twenty models had been developed for multiple use in different settings and for different research questions, while the others were tailored to a specific setting and research question. Most CKD models (n = 31) formed part of larger diabetes models, while the remainder were standalone models. Models had been published over a period of 25 years, from 1996 to 2021, and included 28 cSTM and 21 IPS models (Fig. S3 in the Supplementary Material).

Conceptualization of CKD in Computer Simulation Models of T2DM

State-Transition Models

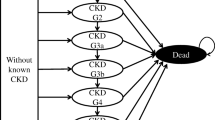
In state-transition models, a structure including five states—one kidney disease-free state, three states with kidney disease, and one death state—was the mostly frequently used, with 16 models adopting this structure from seminal models such as the Eastman et al. [92] and United Kingdom Prospective Diabetes Study (UKPDS) 64 models [103] (Fig. 1).

Fig. 1
figure 1

State-transition diagrams for CKD models in T2DM. CKD, chronic kidney disease; ESKD, end-stage kidney disease; T2DM, type 2 diabetes mellitus. States with borders do not allow loops (patients cannot remain state). Models marked with an asterisk allow regression of renal disease. Plots are ordered by (1) number of states, (2) mean transitions per state (not counting death states and loops), (3) model publication year, and (4) model name in alphabetical order

Full size image

The description of the kidney disease-free state was most often described as normoalbuminuria, “free of renal disease”, or “free of nephropathy”, or as “complication-free diabetes” in larger diabetes models, which included a kidney disease model as a submodel. Some variation was observed in which kidney disease states were modeled. Dating back to the model developed by Eastman et al. [92] (Fig. S4 in the Supplementary Material), microalbuminuria, macroalbuminuria or proteinuria, and ESKD were considered by several models, including by Adarkwah et al. [62], Bagust et al. [76], Golan et al. [80], Wu et al. [110], and the MICADO model [90]. Other models followed the same structure but used different kidney disease states, including the PROSIT ShannonB model [96], which used micro- and macroalbuminuria and a “renal disease” state defined by plasma creatinine ≥ 175 μmol/L; and González et al. [81], which used two ESKD states distinguished by the type of RRT.

In contrast, models such as the UKPDS 64 nephropathy model [103] used the same number of similarly defined states but allowed more transitions, including from the kidney disease-free state directly to more advanced kidney disease states such as macroalbuminuria or elevated plasma creatinine (Fig. S5 in the Supplementary Material). This structure was also used by Palmer et al. [93] and in the Swedish Institute for Health Economics model [85]. An exceptional five-state structure of linear progression from normal renal function through microalbuminuria, clinical nephropathy, and ESKD to death from ESKD was used in the Centers for Disease Control and Prevention cost-effectiveness kidney disease submodel [68], which modeled other diabetes-related outcomes and non-ESKD-related death in its larger diabetes model.

While a five-state model structure was most common, models with as few as three states—modeling pre-ESKD and ESKD states in addition to death [82, 83]—and as many as eight states were identified. Models with more states either modeled CKD in greater detail, e.g., by distinguishing between early and advanced overt nephropathy and different types of RRT [95] or between detected and undetected kidney disease states [102], or by modeling individual CKD stages [12, 78], and/or modeled CKD sequelae such as CVD [65, 100].

Overall, 40 distinct kidney disease states were included by the 28 models, with only five states (microalbuminuria [n = 28], macroalbuminuria [n = 14], ESKD [n = 18], ESKD with transplant [n = 16], and ESKD with dialysis [n = 13]) used by more than ten models. Twenty-five states were used by only one model each, indicating some heterogeneity in how the CKD continuum was modeled in state-transition models.

The three models that explicitly modeled CKD sequelae as part of the CKD model all focused on CVD sequelae [65, 69, 100]. The models by Chen et al. [69] and Smith et al. [100] included a single CVD state, while the model by Campbell et al. [65] included, for each of its four kidney disease states, an additional state combining kidney disease with a CVD event (Fig. S6 in the Supplementary Material).

Regression of renal disease was included in five state-transition models (Fig. 1). The PROSIT ShannonB model [96] allowed regression from macroalbuminuria and microalbuminuria to microalbuminuria and normoalbuminuria, respectively, as did the model developed by Deerochanawong et al. [74] based on the DECLARE-TIME 58 trial for dapagliflozin [111]. The models by Smith et al. [100] and Srisubat et al. [101] allowed for regression from micro- to normoalbuminuria. In the model developed by Delea et al. [75] based on the AVOID Study [112], regression from early overt nephropathy to microalbuminuria and from advanced overt nephropathy to early overt nephropathy and microalbuminuria was modeled during the first 6-month cycle of each overt nephropathy state.

Risk Equations for Kidney Disease Outcomes in IPS Models

Across the 21 IPS models, 20 risk equations were used to predict seven types of kidney disease outcomes, most frequently ESKD/kidney failure (n = 11), albuminuria (n = 5), and eGFR (n = 2).

ESKD/kidney failure occurrence was predicted from 20 different risk factors, most frequently from blood pressure (n = 6), cholesterol, CVD, glycemia (measured using glycated hemoglobin [HbA1c]), and retinopathy (n = 4 each) and from sex (n = 5), age (n = 4), as well as ethnicity and smoking (n = 2) (Fig. S7 in the Supplementary Material). Albuminuria was predicted from 22 different risk factors, most frequently from glycemia (n = 6), blood pressure (n = 4), and cholesterol (n = 3), as well as from sex (n = 5), age (n = 3), and smoking (n = 3). Albuminuria was also predicted on the basis in part of treatment-related factors such as receiving antidiabetic or anticoagulant treatment or SGLT2 inhibitors, but each treatment-related factor was used in at most one risk equation.

Risk Equations Predicting CKD Sequelae in State-Transition and IPS Models

Twenty-two of the 49 models used kidney disease outcomes and markers to predict sequelae and mortality (Fig. S8 in the Supplementary Material). The outcomes most frequently predicted from kidney disease were mortality (n = 21 models), CVD (n = 11), and cerebrovascular disease (n = 6), while ESKD/renal failure (n = 19) and albumin, including albuminuria (n = 10), were the most frequent types of kidney disease outcomes used as predictors. eGFR was used as a predictor by only six models, for CVD (n = 5), mortality (n = 5), and cerebrovascular disease (n = 4).

Primary Data Sources for Modeling CKD in T2DM

Across the 49 models, 158 publications covering 112 primary data sources were identified, including 52 cohort studies, 30 randomized controlled trials (RCT), and 20 registry-based studies (Table S9 in the Supplementary Material). As for models, most primary data sources were from the USA (n = 31) and the UK (n = 11) or were multinational studies (n = 18) (Fig. S9 in the Supplementary Material). A single data source from an African country, Morocco, was identified, while five and seven studies were from China and Japan, respectively.

Network of Models and Primary Sources

The co-occurrence network of models and primary sources revealed a densely connected core of models and sources centered on the US Renal Data System (USRDS) and the UKPDS [113, 114] for clinical and mortality data, and, for clinical data only, the Wisconsin Epidemiological Study of Diabetic Retinopathy (WESDR) [115], and the Rochester Diabetes Project [116] as well as seminal RCTs in diabetic kidney disease including the Irbesartan Diabetic Nephropathy Trial (IDNT) [117], the Irbesartan in Type 2 Diabetes With Microalbuminuria 2 (IRMA-2) trial [118], and the RENAAL trial [119] (Fig. 2 and Fig. S10 in the Supplementary Material).

Fig. 2
figure 2

Model-source co-occurrence network for clinical effects. CKD, chronic kidney disease; ESKD, end-stage kidney disease; T2DM, type 2 diabetes mellitus. Node size is proportional to the indegree (normalized by the number of nodes in the network) so larger nodes indicate higher centrality. Sakthong et al.’s work [99] is classified as both a model and a primary data source as elicited data from experts for development of this model were subsequently used by other models

Full size image

Both centrality indices ranked UKPDS and USRDS among the most central data sources to the kidney disease modeling literature in T2DM for clinical and mortality data, followed by Lewis et al. [120] for clinical data and the Steno-2 study [121] for mortality data (Fig. S11 in the Supplementary Material). Only 13 of the 49 models did not use either UKPDS or USRDS data.

There were five models [70, 72, 83, 88, 109] not connected to the main model-source network component for clinical data and four models [64, 87, 89, 110] that were only loosely connected (Fig. 2). This set of models included the state-transition models by Hayashino et al. [83], for Japan, and by Wu et al. [110], for China, which relied exclusively (in the case of Hayashino et al.) or almost exclusively (in the case of Wu et al.) on country- or Asian-specific data sources instead of sources from American or European countries. The remainder of this set of models included risk equation-based IPS models, which relied on at most two sources for their clinical effectiveness data, either from large clinical management systems (as in the CHIME model [70]) or from large clinical trials (e.g., ACCORD [122] in the BRAVO model [64]) or clinical outcomes trial such as CREDENCE [29] in CREDEM-DKD [72]. With the only exception of the model by Hayashino et al., all risk equation-based IPS models either not connected or loosely connected to the main model-source network had been published since 2018.

Primary Data Sources: Age, Duration of Follow-Up, and Sample Sizes

At the point of model publication, the newest data from the primary sources used in the model were, on average, 13.1 years old (standard deviation [SD] 6.7 years), with minimum and maximum ages ranging from 1.5 years [72] to 28 years [90] (Fig. S12 in the Supplementary Material). The mean calculated follow-up across primary sources was 10.3 years (SD 9.5 years), ranging from less than a year for some observational studies to more than 40 years [123,124,125].

Some of the most central sources identified above were among the older sources but also provided some of the longest follow-up, including the Rochester Diabetes Project, UKPDS, and WESDR studies (Fig. 3).

Fig. 3
figure 3

Age, length of follow-up, and sample size for primary data sources. Each row indicates, for a primary data source, the study start (bubble) and data cuts used in publications for this primary data source (crosses). The bubbles indicating sample sizes are scaled by the logarithm of the baseline sample size of the study. For source abbreviations and citations, see Table S9 in the Supplementary Material

Full size image

There was also a broad trend towards larger sample sizes in more recent primary data sources. The largest sample sizes were from analyses of registry data, including more than 1.1 million adults from the Kaiser Permanente Renal Registry [126], used in the ECHO-T2DM model, and 228,552 adults from the USRDS [127], used in the Syreon Diabetes Control Model [102] and the CORE Diabetes Model [37], as well as the 57,594 patients from the Taiwanese Chronic Disease Management Registry [128], used for modeling by Wu et al. [110], and the 42,495 patients with T2DM from the Hong Kong Health Authority Clinical Management System used by the CHIME simulation model [70]. Other large primary data sources used for modeling were a screening study from Okinawa with 78,529 patients [129], used in the Howard et al. model [84], and large clinical outcomes trials such as DECLARE-TIMI 58 with 17,160 participants [111].

Baseline Characteristics of Derivation Cohorts

Baseline data were available for 1,853,362 participants from 97 primary data sources (Table 2). At baseline, the median age of participants was 58.9 years, while 53% of participants were men. White participants accounted for more than half (50.8%) of all participants, relative to Black and Asian participants, who accounted for 11.5% and 10.1% of all participants, respectively. Half of the participants had never smoked, while 23% were current and 27% were former smokers.

Table 2 Baseline characteristics of derivation cohorts in primary data sources
Full size table

The median reported urinary albumin creatinine ratio was 139.2 mg/g, indicating moderately increased albuminuria (microalbuminuria) (Fig. S13 in the Supplementary Material), while the median eGFR was 84.9 mL/min/1.73 m2, indicating mildly decreased kidney function (Fig. 4) [12].

Fig. 4
figure 4

Estimated glomerular filtration rate at baseline across participants in primary derivation cohorts. Estimated glomerular filtration rate values were weighted by the logarithm of the study sample size (mapped to the size of grey bubbles for individual studies, with a total of 116,636 participants available for analysis) and then summarized. Shading refers to glomerular filtration categories as defined in the KDIGO 2012 Clinical Practice Guideline [12]

Full size image

Median HbA1c was 8.3%, while median systolic and diastolic blood pressure were 135.6 and 79.7 mmHg, respectively (Table 2). The most common comorbidities, as reported in publications at baseline, were hypertension (66%), CVD (41%), and microalbuminuria (29%) (Fig. S14 in the Supplementary Material).

Discussion

To the existing clinical reviews investigating the renoprotective effects of specific compounds or drug classes [28, 30, 32, 33, 130, 131] the present review adds a comprehensive and current overview of computer simulation models of CKD in T2DM and of the data sources and derivation cohorts informing these models.

Regarding model structures and conceptualization of CKD progression, state-transition models of CKD in T2DM were found to frequently employ a five-state structure, for modeling progression from a kidney disease-free state through states with kidney disease to death. While there was some heterogeneity between models in which kidney disease states were chosen, CKD progression in T2DM was modeled almost exclusively on the basis of albuminuria; the one model to use eGFR-based CKD stages as states used a CKD model originally developed for a general, not necessarily diabetic, population [78, 132]. The reliance on albuminuria confirms the observation by Sugrue et al. [34] for a larger set of T2DM models. It is consistent with the classical understanding of kidney disease in diabetes as a sequence of albuminuria states leading to an eventual decline in eGFR and subsequent ESKD [14, 133,134,135].

The other biomarker to define CKD, eGFR, has only more recently been used in CKD models in T2DM. While widely used in general population CKD models that model declining kidney function based on CKD stages defined by eGFR [12, 34, 132], eGFR has only recently received increased attention in CKD models in T2DM as the understanding of eGFR trajectories and their link with albuminuria in patients with diabetes has improved. This understanding includes the non-linear and potentially non-progressive shape of eGFR trajectories, the link between speed of eGFR decline and clinical outcomes, and the possibility for both eGFR and albuminuria to worsen independently of each other [14,15,16,17,18,19,20,21, 136].

Regarding eGFR, renoprotective treatments including SGLT2 inhibitors and glucagon-like peptide 1 (GLP-1) receptor agonists were found to be associated with a transient dip in eGFR upon treatment initiation before eventually slowing eGFR decline [29, 31, 111, 137, 138]. This dip likely reflects intrarenal hemodynamic changes in microcirculation [31, 139] and has also been observed with renin–angiotensin–aldosterone system inhibition [140, 141]. The clinical importance of this transient eGFR dip is not fully understood, but current evidence suggests that it is unlikely to be associated with adverse clinical events [141,142,143].

While the clinical importance of this transient eGFR decline remains to be established and even though an acute phase dip may have little impact over a lifetime modeling horizon, modelers may still wish to allow for this dip when building a model. If models then also consider non-linear eGFR trajectories, their effect on clinical outcomes, and the possibility of CKD regression, modeling CKD in T2DM would quickly reach a complexity that favors risk equation-based IPS over state-transition models as the former can more easily account for non-linear relationships between patient characteristics and model outcomes as well as for heterogeneity between patients [144].

As complex models are not always feasible or preferable to build [145], there may be some interest in reducing complexity when modeling CKD in T2DM, e.g., if sufficient data on clinical outcomes are not available early in a trial or if the model is designed to facilitate communication with wider audiences. One approach adopted in the literature to reduce complexity is to focus on the CKD outcomes associated with the largest clinical—and economic—burden, usually ESKD [8]. Examples include prediction of ESKD from four readily available, not kidney-related clinical characteristics as in the BRAVO risk engine [64], or a simple linear projection of eGFR slopes using a threshold for dialysis initiation as assumed by Durkin and Blais [146]. The latter approach in particular is straightforward to implement and communicate and may suffice to provide an early approximation of intervention effects on the incidence of high-burden events such as ESKD. Alternatively, this could be achieved by developing simple cSTMs that focus on key CKD outcomes and in which robust data for these outcomes compensates for the lack of modeled clinical complexity.

In addition to model structures and CKD disease progression modeling, the review also investigated the data sources and derivation cohorts used by CKD models in T2DM, and potential concerns arising from these findings are discussed here. Several well-established data sources, such as the USRDS, UKPDS, and WESDR, contributed substantially to the clinical effects used in modeling CKD. However, many of these central data sources reported on predominantly White participants from high-income countries in North America and Europe, calling into question their suitability for modeling in underserved populations and in different country settings given differences in the epidemiology, treatment, and prognosis of diabetes and CKD.

In the USA, for example, racial and ethnic minorities are more likely to suffer from diabetes and prediabetes, at lower BMI, than Whites [147, 148]. Minorities were found to be at higher risk of diabetes-related mortality and adverse clinical events, including ESKD, relative to White people in multinational [149] and national studies [150, 151]. Race and ethnicity may also influence whether appropriate care is received for kidney disease; in the UK, for example, adjustment for ethnicity was found to overestimate GFR in self-reported Black participants, thereby potentially delaying the time to treatment initiation [152]. Although note that, in the USA, a National Kidney Foundation and American Society for Nephrology Task Force recently recommended that creatinine equations be refit without a variable for race and that research into GFR estimation aims to eliminate race and ethnic disparities [153]. For people of Asian ethnicity, kidney disease was shown to be a more likely consequence of T2DM than for European and US populations [154], while SGTL2 inhibitors, as an add-on to metformin, were shown to be more efficacious in East Asian patients relative to non-Asian patients with T2DM [155].

These epidemiological and physiological differences in populations with diabetes and/or CKD have led to calls for modeling that is more sensitive to these differences [156], which have recently been heeded as a number of models have been developed specifically for Asian settings using data not derived from US or European populations. In Fig. 2, they can be seen on the edge of (or entirely disconnected from) the model-source co-occurrence network, and include the CHIME model, based on data from Hong Kong [70], the JJCEM, based on data from Japan [87], the model by Watada et al. [109], based on Asian patients from the CARMELINA trial [157], and the models by Hayashino et al. [83] and Wu et al. [110].

Some established data sources may be questioned regarding not only their racial and ethnical representativeness but also their relevance for current clinical practice, as a result of their age. The UKPDS, for example, was initiated in 1977, while key trials such as IDNT, IRMA-2, and RENAAL were begun in the 1990s and completed by the early 2000s. Concerns about the age of the UKPDS data, for example, motivated the development of the BRAVO risk engine from ACCORD data [64]. These concerns may be less urgent than they may initially seem, however, as studies with long and comprehensive follow-up necessarily need to have started longer ago. Provided that the models based on these studies can discriminate well between patients and/or cohorts, there is nothing to preclude their use in modern patient populations, particularly after appropriate calibration [158]. This review also identified several models developed from clinical outcomes trials soon after trial completion, including the CREDEM-DKD model [72] and the models by Kansal et al. [88] and Watada et al. [109], which may represent a beginning trend to develop disease models quickly from outcomes trials. Such trials may provide not only recent but also comprehensive data on a wide range of biomarkers that would allow to build CKD and indeed full diabetes models from a single consistent data source. As findings from clinical trials may not readily be generalizable to non-trial populations, using only trial data to develop models could limit a model’s scope and usefulness although trials could be specifically designed to include participants from previously understudied populations [159].

The present review has some limitations. Searches in literature databases were limited to PubMed (including MEDLINE), Embase, and the Cochrane Library, which are recommended for consideration in systematic reviews but may have missed computer simulation models published in non-English language or non-indexed journals, possibly biasing the set of models available for inclusion [160]. The review also relied exclusively on published and publicly available information, meaning that models that are already fully operational but not (yet) described in a published paper or technical report and unpublished model updates were missed. A further limitation of the review was that 90% of titles and abstracts were screened and all full texts reviewed by a single researcher, potentially increasing the risk of inadvertently excluding relevant studies relative to two reviewers screening all studies independently.

Grouping models for analyses and synthesizing study results was also limited by inconsistent terminology and modeling approaches (which, as previously observed by Sugrue et al. [34], were rarely justified), and differences in the level of detail provided. A limitation in the assessment of baseline characteristics of derivation cohorts was that all primary data sources with baseline data available were treated equally (after weighting by sample size) so data from a source informing a single data point in a single model received the same weight as data from a source informing dozens of data points across several models. While also weighting by network centrality was considered, this would have required redrawing networks and recalculating indices for each outcome as not all outcomes were reported by all studies. Different summary measures would then have been based on different networks with limited comparability of either networks or summary measures. Data sources were therefore treated equally, and readers should bear this in mind when considering results for baseline characteristics.

Conclusion

As novel renoprotective treatments for CKD in patients with T2DM become available, the modeling of CKD progression in T2DM has become ever more important to inform clinical and economic decision-making. The accuracy of such modeling will likely increase through recent and future improvements in the understanding of CKD and T2DM and through larger and more robust data. As increasingly detailed data are gathered, modelers may consider developing complex models that allow one to track CKD progression and outcomes in increasing detail. Modelers should not lose sight, however, of using these data to populate or develop simpler models, e.g., those focusing on the clinically and economically most relevant endpoints, or to inform the link between surrogate endpoints and clinical outcomes [161]. Simpler models may not capture as many details but may still be sufficient to model outcomes reliably (in some cases even more accurately than complex models [145]), may be more familiar to clinical and health technology assessment audiences, and may be easier to communicate and interpret. The present review provides a comprehensive and contemporary overview of modeling approaches and data sources that modelers can use to explore different modeling options and to inform the development of any future models of CKD in patients with T2DM.