Abstract
The AMMI/GGE model can be used to describe a two-way table of genotype–environment means. When the genotype–environment means are independent and homoscedastic, ordinary least squares (OLS) gives optimal estimates of the model. In plant breeding, the assumption of independence and homoscedasticity of the genotype–environment means is frequently violated, however, such that generalized least squares (GLS) estimation is more appropriate. This paper introduces three different GLS algorithms that use a weighting matrix to take the correlation between the genotype–environment means as well as heteroscedasticity into account. To investigate the effectiveness of the GLS estimation, the proposed algorithms were implemented using three different weighting matrices, including (i) an identity matrix (OLS estimation), (ii) an approximation of the complete inverse covariance matrix of the genotype–environment means, and (iii) the complete inverse covariance matrix of the genotype–environment means. Using simulated data modeled on real experiments, the different weighting methods were compared in terms of the mean-squared error of the genotype–environment means, interaction effects, and singular vectors. The results show that weighted estimation generally outperformed unweighted estimation in terms of the mean-squared error. Furthermore, the effectiveness of the weighted estimation increased when the heterogeneity of the variances of the genotype–environment means increased.



Similar content being viewed by others
References
Besag, J., and Higdon, D. (1999), “Bayesian analysis of agricultural field experiments,” Journal of the Royal Statistical Society. Series B (Statistical Methodology), 61, 691–746. https://doi.org/10.1111/1467-9868.00201
Bro, R., Kjeldahl, K., Smilde, A.K., and Kiers, H.A.L. (2008), “Cross-validation of component models: A critical look at current methods,” Analytical and Bioanalytical Chemistry, 390, 1241–1251. https://doi.org/10.1007/s00216-007-1790-1
Caliński, T., Czajka, S., Denis, J.B., and Kaczmarek, Z. (1992), “EM and ALS algorithms applied to estimation of missing data in series of variety trials,” Biuletyn Oceny Odmian, 24–25, 8–31.
Cornelius, P.L., Seydsadr, M., and Crossa, J. (1992), “Using the shifted multiplicative model to search for separability in crop cultivar trials,” Theoretical and Applied Genetics, 84, 161–172. https://doi.org/10.1007/BF00223996
Damesa, M.T., Möhring, J., Worku, M., and Piepho, H.P. (2017), “One step at a time: Stage wise analysis of a series of experiments,” Agronomy Journal, 109, 845–857. https://doi.org/10.2134/agronj2016.07.0395
Dias, C.T.d.S., and Krzanowski, W.J. (2003), “Model selection and cross validation in additive main effect and multiplicative interaction models,” Crop Science, 43, 865–873. https://doi.org/10.2135/cropsci2003.8650
Digby, P.G.N., and Kempton, R.A. (1987), “Multivariate analysis of ecological communities,” Chapman & Hall, London.
Forkman, J., and Piepho, H.P. (2014), “Parametric bootstrap methods for testing multiplicative terms in GGE and AMMI models,” Biometrics, 70, 639–647. https://doi.org/10.1111/biom.12162
Gabriel, K.R., and Zamir, S. (1979), “Lower rank approximation of matrices by least squares with any choice of weights,”Technometrics, 21, 489–498.
Gauch, H.G. Jr. (1988), “Model selection and validation for yield trials with interaction,” Biometrics, 44, 705–715. https://doi.org/10.2307/2531585
Gauch, H.G. Jr., and Zobel, R.W. (1990), “Imputing missing yield trial data,” Theoretical and Applied Genetics, 79, 753–761.
Gauch, H.G. Jr. (1992), “Statistical analysis of regional yield trials,” Elsevier Science Publishers, Amsterdam.
Gollob, H.F. (1968), “A Statistical model which combines features of factor analytic and analysis of variance techniques,” Psychometrika, 33, 73–115. https://doi.org/10.1007/BF02289676
Green, B.F. (1952), “The orthogonal approximation of an oblique structure in factor analysis,” Psychometrika, 17, 429–440.
Hadasch, S., Forkman, J., Piepho, H.P. (2016), “Cross-validation in AMMI and GGE models: A comparison of methods,” Crop Science, 57, 264–274. https://doi.org/10.2135/cropsci2016.07.0613.
Josse, J., van Eeuwijk, F.A., and Piepho, H.P., Denis, J.B. (2014), “Another look at Bayesian analysis of AMMI models for genotype–environment data,” Journal of Agricultural, Biological, and Environmental Statistics, 19, 240–257.
Kotz, S., Balakrishnan, N., Read, C.B., Vidakovic, B., and Johnson, N.L. (2006), “Encyclopedia of statistical sciences, second edition ”John Wiley & Sons, John Wiley & Sons, Hoboken, New Jersey.
Kruskal, J. B. (1965), “Analysis of factorial experiments by estimating monotonic transformations of the data,” Journal of the Royal Statistical Society, 27, 251–263.
Mandel, J. (1969), “The partitioning of interaction in analysis of variance,” Technometrics, 73, 309–328.
Meng, X.L., and Rubin, D.B. (1993), “Maximum likelihood estimation via the ECM algorithm: A general framework,” Biometrika, 80, 267–278.
Perez-Elizalde, S., Jarquin, D., and Crossa, J. (2012), “A general Bayesian estimation method of linear–bilinear models applied to plant breeding trials with genotype x environment interaction,” Journal of Agricultural, Biological, and Environmental Statistics, 17, 15–37. https://doi.org/10.1007/s13253-011-0063-9
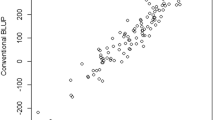
Piepho, H.P. (1994), “Best linear unbiased prediction (BLUP) for regional yield trials: a comparison to additive main effects and multiplicative interaction (AMMI) analysis,” Theoretical and Applied Genetics, 89, 647–654. https://doi.org/10.1007/BF00222462
Piepho, H.P. (1997), “Analyzing genotype-environment data by mixed models with multiplicative effects” Biometrics, 53, 761–766. https://doi.org/10.2307/2533976
Piepho, H.P. (2004), “An algorithm for a letter-based representation of all-pairwise comparisons,” Journal of Computational and Graphical Statistics, 13, 456–466.
Piepho, H.P., Möhring, J., Schulz-Streeck, T., and Ogutu, J.O. (2012), “A stage-wise approach for the analysis of multi-environment trials,”Biometrical Journal, 54, 844–860. https://doi.org/10.1002/bimj.201100219
Rodrigues, P.C., Malosetti, M., Gauch, H.G. Jr., and van Eeuwijk, F.A. (2014), “A weighted AMMI algorithm to study genotype-by-environment interaction and QTL-by-environment interaction,”Crop Science, 54, 1555–1569. https://doi.org/10.2135/cropsci2013.07.0462
Schönemann, P.H. (1966), “A generalized solution to the orthogonal procrustes problem,” Psychometrica. https://doi.org/10.1007/BF02289451.
Searle, S.R, Casella, G., and McCulloch, C.E. (1992), “Variance components,”John Wiley & Sons, New York.
Smith, A., Cullis, B., and Gilmour, A. (2001a), “The analysis of cop variety evaluation data in Australia,” Australian and New Zealand Journal of Statistics, 43, 129–145. https://doi.org/10.1111/1467-842X.00163
Smith, A., Cullis, B.R., and Thompson, R. (2001b), “Analysing variety by environment data using multiplicative mixed models and adjustment for spatial field trend,” Biometrics, 57, 1138–1147. https://doi.org/10.1111/j.0006-341X.2001.01138.x
Srebro, N., and Jaakkola, T. (2003), “Weighted low-rank approximations,” Proceedings of the Twentieth International Conference on Machine Learning, Washington DC.
Yan, W., Hunt, L.A., Sheng, Q., and Szlavnics, Z. (2000), “Cultivar evaluation and mega-environment investigation based on the GGE Biplot,”Crop Science, 40, 597–605. https://doi.org/10.2135/cropsci2000.403597x
Yan, W., and Kang, M.S. (2002), “GGE biplot analysis,” CRC Press, Boca Raton.
Author information
Authors and Affiliations
Corresponding author
Electronic supplementary material
Below is the link to the electronic supplementary material.
Appendices
Appendix
The criss-cross algorithm describes matrix \({{\varvec{H}}}=({{\varvec{h}}}_1\ldots {{\varvec{h}}}_J)\) by the model \({{\varvec{H}}}={{{\varvec{GF}}}}'+{{\varvec{E}}}\) where \({{\varvec{E}}}\) is a random error. The matrices \({{\varvec{G}}}\) and \({{\varvec{F}}}\) both consist of n columns such that the product \({{{\varvec{GF}}}}'\) represents a rank n approximation of \({{\varvec{H}}}\). The algorithm makes particular use of the fact that \({{\varvec{H}}}\) is linear in \({{\varvec{F}}}'\) for a given matrix \({{\varvec{G}}}\) and vice versa. Using \({{\varvec{vec}}}({{\varvec{H}}})=({{\varvec{h}}}_1^{\prime } \ldots {{\varvec{h}}}_J^{\prime })^{{\prime }}={{\varvec{h}}}\) (Searle et al. 1992), and \({{\varvec{vec}}}({{{\varvec{GF}}}}')=({{\varvec{I}}}_{{\textit{n}}}\otimes {{\varvec{G}}}){{\varvec{vec}}}({{\varvec{F}}'}) =({{\varvec{F}}}\otimes {{\varvec{I}}}_{{\textit{n}}}){{\varvec{vec}}}({{\varvec{G}}})\), the model can be written as
where \({{\varvec{X}}}_{{\varvec{f}}} = ({{\varvec{I}}}_{\textit{n}} \otimes {{\varvec{G}}}), {{\varvec{f}}}={{\varvec{vec}}}({{{\varvec{F}}}}'), {{\varvec{X}}}_{{\varvec{g}}} =({{\varvec{F}}}\otimes {{\varvec{I}}}_{\textit{n}} ), {{\varvec{g}}}={{\varvec{vec}}}({{\varvec{G}}})\), and \({\varvec{\varepsilon }} ={{\varvec{vec}}}({{\varvec{E}}})\). These two models for \({{\varvec{h}}}\) can be used alternatingly to estimate \({{\varvec{G}}}\) and \({{\varvec{F}}}\) by minimizing \({\varvec{\varepsilon }}^{\prime }{{\varvec{M}}}{\varvec{\varepsilon }}\), where \({{\varvec{M}}}\) is a weighting matrix. For this purpose, \({{\varvec{G}}}\) may initialized by a nonzero matrix to compute an estimate of \({{\varvec{F}}}\) which in turn is used to update \({{\varvec{G}}}\). In this way, the GLS estimates in the zth iteration are
where \({{\varvec{X}}}_{{\varvec{f}}} =({{\varvec{I}}}_{\textit{n}} \otimes {{\varvec{G}}}^{{\textit{z}}-{1}})\), and \({{\varvec{X}}}_{{\varvec{g}}} =({{\varvec{F}}}^{{\textit{z}}}\otimes {{\varvec{I}}}_{\textit{n}})\). One could equivalently start the algorithm by initializing \({{\varvec{F}}}\). To estimate the AMMI/GGE model by criss-cross algorithm, all the effects of the AMMI/GGE model are estimated iteratively. In particular, the interaction of the AMMI/GGE model is reparameterized and the effects of the reparameterized model are estimated iteratively. In matrix form, the reparameterized model for the observed genotype–environment means using n multiplicative terms is
where \({{\varvec{A}}}\) and \({{\varvec{B}}}\) consist of n columns and the product \({{\varvec{AB}}}'\) models the interaction effects \({{\varvec{W}}}(N)\) in (2). Using the \(vec\left( \cdot \right) \) operator, the equation can be written as
where \(\hat{{\varvec{\theta }}} =vec(\hat{{\varvec{\varTheta }}}(n))\), \({{\varvec{X}}}_\mu =\mathbf{1}_{IJ}, {{\varvec{X}}}_{{\varvec{g}}} =(\mathbf{1}_J \otimes {{\varvec{I}}}_I)\), \({{\varvec{X}}}_{{\varvec{e}}} =({{\varvec{I}}}_J \otimes \mathbf{1}_I)\), \({{\varvec{X}}}_{{\varvec{b}}} = ({{\varvec{I}}}_J \otimes {{\varvec{A}}})\), \({{\varvec{b}}}=vec({{\varvec{B}}}')\), and \({\varvec{\varepsilon }} =vec({{\varvec{E}}})\). The iteration can be started by initializing \({{\varvec{A}}}\) in (4) to estimate \({{\varvec{b}}}\) by minimizing \({\varvec{\varepsilon }}^{\prime }{{\varvec{M}}}{\varvec{\varepsilon }}\), where \({{\varvec{M}}}\) is a weighting matrix. In the zth iteration, the system of equations resulting from the derivatives of \({\varvec{\varepsilon }}^{\prime }{{\varvec{M}}}{\varvec{\varepsilon }}\) is
where \({{\varvec{X}}}_{{\varvec{b}}} =({{\varvec{I}}}_J \otimes {{\varvec{A}}}^{z-1})\). To estimate \({{\varvec{a}}}=vec({{\varvec{A}}})\), the term \({{\varvec{X}}}_{{\varvec{b}}} {{\varvec{b}}}\) in (4) is replaced by \({{\varvec{X}}}_{{\varvec{a}}} {{\varvec{a}}}=({{\varvec{B}}}^{{\textit{z}}}\otimes {{\varvec{I}}}_I){{\varvec{a}}}\). In this case, the system of equations is
In this way, the model effects are estimated alternatingly until the change in the estimated genotype–environment means in two successive iterations is lower than a certain threshold (for details, see Figures 1, 2 and 3). The two equation systems can be solved in different ways. Here, we use three different algorithms to solve it, which will be denoted by Algorithm 1–3.
Algorithm 1
In Algorithm 1, the system of equations resulting from derivatives of \({\varvec{\varepsilon }}'{{\varvec{M}}}{\varvec{\varepsilon }}\) with regard to the model effects is inverted using a generalized inverse. For a given matrix \({{\varvec{A}}}\), the estimated effects of the AMMI model in the zth iteration can be displayed by
where \({{\varvec{X}}}_{{\varvec{b}}} =({{\varvec{I}}}_J \otimes {{\varvec{A}}}^{z-1})\) and \((\cdot )^{-}\) is a generalized inverse. The estimates of \(\mu , {{\varvec{e}}}\), and \({{\varvec{b}}}\) are reparameterized by \(\tilde{\mu }=\mu +\frac{1}{J}{} \mathbf{1}_J^{\prime } {{\varvec{e}}}+\frac{1}{I}{} \mathbf{1}_I^{\prime } {{\varvec{g}}}, \tilde{e} ={{\varvec{e}}}-\frac{1}{J}{} \mathbf{1}_J \mathbf{1}_J^{\prime } {{\varvec{{{\varvec{e}}}}}}\), and \(\tilde{{{\varvec{B}}}}={{\varvec{B}}}-\frac{1}{J}{} \mathbf{1}_J \mathbf{1}_J^{\prime } {{\varvec{B}}}\). For a given estimate of \(\tilde{{{\varvec{B}}}}\), the effects \({{\varvec{g}}}\), and \({{\varvec{a}}}\) were estimated by
where \({{\varvec{X}}}_{{\varvec{a}}} =(\tilde{{{\varvec{B}}}}^{{{\varvec{z}}}}\otimes {{\varvec{I}}}_I)\). The estimates of \({{\varvec{g}}}\) and \({{\varvec{a}}}\) are reparameterized by \(\tilde{{{\varvec{g}}}}={{\varvec{g}}} -\frac{1}{I}{} \mathbf{1}_I \mathbf{1}_I^{\prime } {{\varvec{g}}}\), and \(\tilde{{{\varvec{A}}}}={{\varvec{A}}}-\frac{1}{I}{} \mathbf{1}_I \mathbf{1}_I^{\prime } {{\varvec{A}}}\) . The estimated genotype–environment means are then obtained by \(\hat{{\varvec{\theta }}} (n) =\tilde{\mu }{{\varvec{X}}}_\mu +{{\varvec{X}}}_{{\varvec{g}}} \tilde{{{\varvec{g}}}} +{{\varvec{X}}}_{{\varvec{e}}} \tilde{{{\varvec{e}}}}+{{\varvec{X}}}_{{\varvec{b}}} \tilde{{{\varvec{b}}}}\). In case of the GGE model, the main genotype effects are not estimated and the estimates of \({{\varvec{B}}}\) are not reparameterized.
Algorithm 2
In Algorithm 2, the two systems of equations were solved using the Jacobi iterative method (Kotz et al. 2006) and the sum-to-zero constraints were implemented using the method of Lagrange multipliers. In the Jacobi iteration, the solution of an equation system of the form
where \({{\varvec{y}}}\) is a vector of observations, \({{\varvec{X}}}_1 \) and \({{\varvec{X}}}_2 \) are design matrices for the parameter vectors \({{\varvec{b}}}_1 \) and \({{\varvec{b}}}_2 \), which is obtained by iteratively computing
When constraints on the parameters need to be imposed, the Lagrange multipliers need to be included in the objective function that is to be minimized. In case of the AMMI/GGE model, the objective function becomes \({\varvec{\varepsilon }}'{{\varvec{M}}}{\varvec{\varepsilon }} +{{\varvec{P}}}'{{\varvec{l}}}\) where \({{\varvec{l}}}\) is a vector of Lagrange multipliers and \({{\varvec{P}}}'\) the matrix containing the coefficients for the desired linear constraint. When the Lagrange multipliers are included in the objective function, the system of equations takes the form
where \(({{\varvec{P}}}_1^{\prime } {{\varvec{P}}}_2^{\prime }) \left( \begin{array}{l} {{\varvec{b}}}_1 \\ {{\varvec{b}}}_2 \\ \end{array}\right) ={{\varvec{c}}}\) represents the desired constraints. Using the Jacobi iteration to solve that system, one may write
Obviously, the Lagrange multipliers cannot be updated from the equation above. Instead, the Lagrange multipliers \({{\varvec{l}}}^{z-1}\) can be found by solving \(({{\varvec{P}}}_1^{\prime } {{\varvec{P}}}_2^{\prime }) \left( \begin{array}{l} {{\varvec{b}}}_1^z \\ {{{\varvec{b}}}_2^z } \\ \end{array}\right) =c\) for \({{\varvec{l}}}^{z-1}\) and plugging the solution back into \(\left( \begin{array}{l} {{{\varvec{b}}}_1^z } \\ {{{\varvec{b}}}_2^z } \\ \end{array}\right) \). With \({{\varvec{c}}}=\mathbf{0}\), which represents sum-to-zero constraints, this yields
where \({{\varvec{D}}}^{-1}=\left( {{\begin{array}{ll} ({{\varvec{X}}}_1^{\prime } {{\varvec{X}}}_1 )^{-1} &{} \mathbf{0} \\ \mathbf{0} &{} ( {{\varvec{X}}}_2^{\prime } {{\varvec{X}}}_2 )^{-1} \\ \end{array} }} \right) \) and \({{\varvec{P}}}=\left( {{\begin{array}{l} {{{\varvec{P}}}_1} \\ {{{\varvec{P}}}_2} \\ \end{array} }} \right) \). When \({{\varvec{P}}}\) can be partitioned as \({{\varvec{P}}}=\left( {{\begin{array}{ll} {{{\varvec{Q}}}_1 } &{} \mathbf{0} \\ \mathbf{0} &{} {{{\varvec{Q}}}_2 } \\ \end{array} }} \right) \), which is the case for the constraints in AMMI/GGE models, the estimates in the zth iteration are
where \({{\varvec{R}}}_1 =({{{\varvec{X}}}_1^{\prime } {{\varvec{X}}}_1 } )^{-1} {{\varvec{Q}}}_1 ({{{\varvec{Q}}}_1^{\prime } ({{{\varvec{X}}}_1^{\prime } {{\varvec{X}}}_1 } )^{-1}{{\varvec{Q}}}_1 } )^{-1}{{\varvec{Q}}}_1^{\prime } \), and \({{\varvec{R}}}_2=({{{\varvec{X}}}_2^{\prime } {{\varvec{X}}}_2})^{-1} {{\varvec{Q}}}_2 ({{\varvec{Q}}}_2^{\prime }({{{\varvec{X}}}_2^{\prime } {{\varvec{X}}}_2})^{-1}{{\varvec{Q}}}_2)^{-1}{{\varvec{Q}}}_2^{\prime }\). These estimates can be used for weighted estimation of the AMMI/GGE model by the criss-cross algorithm. Starting the algorithm by initializing \({{\varvec{A}}}\), the estimates in the zth iteration are
where \({{\varvec{X}}}_{{\varvec{a}}} =({{{\varvec{B}}}^{z}\otimes {{\varvec{I}}}_I}), {{\varvec{X}}}_{{\varvec{b}}} =({{{\varvec{I}}}_J \otimes {{\varvec{A}}}^{z-1}}), {{\varvec{Q}}}_{{\varvec{e}}} =\mathbf{1}_J, {{\varvec{Q}}}_{{\varvec{g}}} =\mathbf{1}_I, {{\varvec{Q}}}_{{\varvec{b}}} =({\mathbf{1}_J \otimes {{\varvec{I}}}_n })\), and \({{\varvec{Q}}}_{{\varvec{a}}} =({{{\varvec{I}}}_n \otimes \mathbf{1}_I } )\).
The convergence of this iterative algorithm can be accelerated by using the effects that were already estimated in the zth iteration to estimate the subsequent effects, e.g., using \(\mu ^{z}\) to estimate \({{\varvec{e}}}^{z}\) (Figure 2).
Algorithm 3
This algorithm was also implemented by the Jacobi iterative method. The difference to Algorithm 2 is that the weighted SVD proposed by Rodrigues et al. (2014) was used to estimate the multiplicative interaction. In matrix form, the weighted SVD (Rodrigues et al. 2014) is computed by
where \({{\varvec{Z}}}\) is the data, \({{\varvec{M}}}\) is a matrix containing weights which are smaller than or equal to one, \({{\varvec{W}}}_{\mathrm{SVD}}^{z-1} \) are the estimated interaction effects in the \(({z-1})\)th iteration using n multiplicative terms, \(\odot \) is the Hadamard (or element-wise) product of matrices, and SVD\([\cdot ]\) represents the SVD of a matrix. Using the \(vec(\cdot )\) operator, the argument of the SVD can be written as
where \({{\varvec{D}}}\) is a diagonal matrix containing the elements of \({{\varvec{M}}}\) on the diagonal. In this representation, any non-diagonal \({{\varvec{D}}}\) may also be used to estimate \({{\varvec{W}}}_{\mathrm{SVD}}\) by the proposed weighted SVD of Rodrigues et al. (2014). The iterative estimation of \({{\varvec{W}}}_{\mathrm{SVD}}\) may be incorporated in the Jacobi iteration by replacing the estimates of \({{\varvec{a}}}^{z}\) and \({{\varvec{b}}}^{z}\) in Algorithm 2 by \(vec({{{\varvec{W}}}_{\mathrm{SVD}}^z })\) and by replacing \({{\varvec{X}}}_{{\varvec{b}}} {{\varvec{b}}}^{z-1}\) by \(vec({{{\varvec{W}}}_{\mathrm{SVD}}^{z-1} })\). In the Jacobi iteration proposed here, we used \({{\varvec{Z}}}=\hat{{\varvec{\varTheta }}} -\mu ^{z} \mathbf{1}_I \mathbf{1}_J^{\prime } - {{\varvec{g}}} ^{{{\varvec{z}}}} \mathbf{1}_J^{\prime } -\mathbf{1}_I {{\varvec{e}}^{\prime }}^{z}\) to compute the weighted SVD. Due to the weights, the data subjected to the SVD may not be row- and column-centered; therefore, the left and right singular vectors of the SVD of \({{\varvec{W}}}_{\mathrm{SVD}}^z\) need to be centered to establish the constraints of the AMMI/GGE model (Figure 3).
Rights and permissions
About this article
Cite this article
Hadasch, S., Forkman, J., Malik, W.A. et al. Weighted Estimation of AMMI and GGE Models. JABES 23, 255–275 (2018). https://doi.org/10.1007/s13253-018-0323-z
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s13253-018-0323-z